基于定量反馈理论的气动调节阀控制系统设计

夏 勤，方 星,2，刘 飞

(1.江南大学轻工过程先进控制教育部重点实验室，江苏 无锡 214122; 2.无锡气动技术研究所有限公司，江苏 无锡 214072)

0 引言

气动调节阀是现代工业过程控制系统中不可或缺的重要设备，其性能会直接影响整个工业过程。气动调节阀往往在复杂环境中工作，常受到外界干扰和内部等价干扰(包括模型不确定性、未建模动态等)的影响。因此，气动调节阀系统控制器的鲁棒性要求一般较高。

气动调节阀系统目前应用的控制算法主要有：常规比例积分微分(proportional integral defferential,PID)控制算法和基于PID改进的控制算法，例如模糊-PID控制、灰色预测模糊PID控制等。文献[1]应用了1种PID参数整定方案，在Ziegler-Nichols整定基础上设计了PID参数整定算法。该算法能够有效地减小气动调节阀系统的超调，但不能够较好地满足该系统在外部干扰和模型不确定性影响下的性能指标要求，而且当被控对象的参数发生变化时其控制效果较差。文献[2]应用了1种模糊-PID控制算法。该算法将模糊算法与常规PID相结合，能够针对被控对象的参数变化进行自动调节。但模糊控制器具有滞后特性，且不能有效地利用已知的对象模型及其不确定性信息。文献[3]介绍了灰色预测模糊PID控制算法。该算法具有“超前控制”的特性，能对系统数据进行提取并预测其发展趋势，从而改善滞后问题。但灰色预测模糊PID控制算法仍不能有效利用已知的对象模型及其不确定性信息。

针对以上情况，本文将定量反馈理论(quantitative feedback theory,QFT)控制方法应用于气动调节阀控制系统，从而利用已知的对象模型及其不确定性信息对系统进行控制器设计。

1 气动调节阀控制系统的数学模型

由于气动调节阀控制系统结构较复杂[4-5]，采用系统整体建模的方法难度较大，所以本文按照气动调节阀的组成将系统划分为不同的功能模块。相对于系统整体建模的方法，模块化建模手段更加简单和高效，而且模块化的模型也具有更好的移植性和扩展性。因此，根据工作流程，按照模块化思想，将气动调节阀控制系统划分为智能定位器模块和阀门执行器模块。本文选取的阀门执行器为反作用气动薄膜式调节阀。气动调节阀控制系统模块化分析如图1所示。

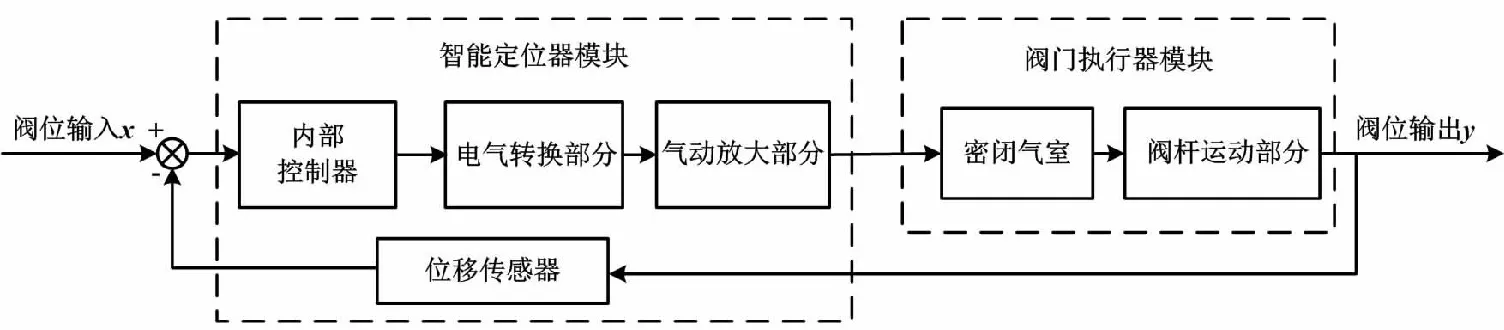
图1 气动调节阀控制系统模块化分析框图Fig.1 Modular analysis block diagram of pneumatic control valve control system

以下按照智能定位器模块与阀门执行器模块，分别建立气动调节阀控制系统的数学模型。

1.1 智能定位器模块

智能定位器模块包括内部控制器、电气转换部分、气动放大部分和阀位反馈部分(位移传感器)。通常，阀位反馈部分(位移传感器)的传递函数为R(s)=1。电气转换部分与气动放大部分结构较为复杂，涉及较多的空气动力学相关知识，难以直接建立其机理模型。因此，通常采用系统辨识的方法建立智能定位器模块的数学模型。

通常，电气转换部分与气动放大部分可以建模为以下的二阶系统[6]：

(1)

式中：K为二阶系统增益；ξ为二阶系统阻尼系数；s为拉普拉斯算子；ω为二阶系统自然振荡频率。

1.2 阀门执行器模块

阀门执行器模块由密闭气室和阀杆运动部分组成。本文将通过机理建模方法得到该模块的数学模型。这部分的机理模型可分为3个部分，分别为气室气压转换部分、气压与力的转换部分，以及气动薄膜式调节阀位移转换部分[7]。

1.2.1 气室气压转换部分

阀门执行器模块的气室可理解为将输入的气压信号转换为气室内压力的部分，近似为阻容部分。该部分理想气体等温状态下的弹性模量计算式为：

(2)

式中：Kv为理想气体等温弹性模量；ΔP为气室内压力变化值；ΔV为压缩后气体体积的变化值；V为压缩前气体的体积。

式(2)整理后可得：

(3)

(4)

式中：Qi为气体流入流量;Qo为气体流出流量;P2为气室内压强。

在气体流速不高时，气体流量与压差之间有以下近似关系：

(5)

式中：P1为输入气压；Rv为导气气阻。

由于气动薄膜执行机构的气室是封闭的，则输出流量Qo=0。将式(4)代入式(5)中，经整理并进行增量化处理后可得：

(6)

为了简化模型的书写，将增量符号省略，则式(6)可表示为：

(7)

式中：Tv为Rv和Cv的乘积。

对上述一阶微分方程式(6)进行拉氏变换，可得：

Tv×sP2(s)+P2(s)=P1(s)

(8)

由此可得气动薄膜执行机构气室的传递函数：

(9)

1.2.2 气压与力的转换部分

气压与力的转换部分是将气室内气压转换为执行机构推杆的拉力。力的大小与气室内膜片的有效面积AD有关，可以表示为：

F(t)=P2(t)AD

(10)

式(10)为比例部分。对其进行拉氏变换，可得：

F(s)=P2(s)×AD

(11)

将式(11)转换为传递函数的形式，可得：

(12)

1.2.3 气动薄膜式调节阀的位移转换部分

气动薄膜式调节阀的位移转换部分可以近似为质量-弹簧-阻尼系统。气动薄膜执行机构及其力学分析如图2所示。

图2 气动薄膜执行机构及其力学分析图Fig.2 Pneumatic membrane actuator and its mechanical analysis diagram

根据牛顿第二定律，气室输出力的系统方程为：

(13)

式中：m为执行机构运动部件的总质量；x为执行机构的输出位移；k为执行机构弹簧的弹性系数；b为执行机构的内摩擦阻尼。

在零初始条件下进行拉氏变换，整理后可以得到气室输出力与阀杆位移的传递函数：

(14)

综上所述，通过对智能定位器模块及阀门执行器模块进行建模分析，可得到气动调节阀控制系统的数学模型由式(1)、式(7)、式(10)和式(12)构成：

G(s)=G1(s)G2(s)G3(s)G4(s)

(15)

2 气动调节阀控制系统的QFT控制器设计

QFT是1种基于鲁棒控制思路的设计理论。在设计控制器之前，将系统已知的不确定性信息和需要达到的性能指标以定量的形式进行描述，然后根据上述限定条件设计能够容忍前述不确定性并且满足性能指标的控制器，从而使得控制系统具有较好的鲁棒性。因此，QFT被广泛应用于具有严重不确定性的系统中。经过近几十年的发展，QFT被应用于各种实际工程系统，如飞机的鲁棒飞行控制系统设计[8]、液压履带车辆驱动系统的鲁棒控制[9]、永磁同步电机伺服系统[10]等。

气动调节阀的模型参数在实际工程中会由于工况变化、环境因素等原因出现频繁摄动，而利用QFT能够很好地解决模型参数摄动的问题。在基于QFT的二自由度控制器设计过程中，将已知模型参数的摄动和系统的性能指标要求等条件考虑在内，能够使系统具有较强的鲁棒性。

2.1 QFT系统结构

QFT由Horowitz开发，是对经典频率鲁棒控制设计方法的扩展[11]。QFT控制器是1种两自由度结构，包含1个前置滤波器和1个反馈控制器。QFT控制原理如图3所示。

图3 QFT控制原理框图Fig.3 QFT control principle block diagram

图3中，x、y、d1、d2分别为系统的参考输入、参考输出、输入扰动和输出扰动。QFT的最终目标是为具有不确定性的被控对象设计1个两自由度的鲁棒控制器，确保系统即使存在输入输出扰动，其频域响应仍能满足性能指标要求[12]。

2.2 气动调节阀的对象模板和标称对象

针对本文研究的气动调节阀控制系统，得到系统的传递函数为：

(16)

(17)

G3(s)=65

(18)

(19)

实测不确定参数范围为：m∈[0.04 0.05]kg；k∈[8 10]N/mm；b∈[0.8 1]N /(mm/s)。

选取m0=0.05 kg、k0=10 N/mm、b0=1 N/(mm/s)作为系统的标称参数，得到标称对象的传递函数为：

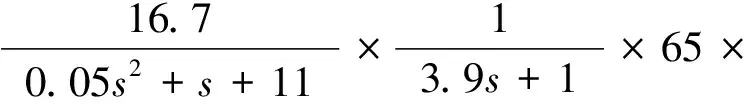
(20)

2.3 气动调节阀的性能指标设计

根据气动调节阀控制系统的动态特性要求，可得闭环系统阶跃响应的调节时间ts≤2.5 s、上升时间tP≤1.5 s、超调量σ≤5%、相角裕度φm≥49°、幅值裕度km≥5 dB。由此确认设计性能指标如下。

2.3.1 鲁棒稳定性指标

(21)

式中：L(jω)=C(jω)×G0(jω)×C(jω)为待设计的反馈控制器。

(22)

(23)

式(22)、式(23)可保证系统的最小幅值裕度KM为5.26 dB，最小相位裕度φM为49°，满足鲁棒稳定性要求。

2.3.2 跟踪性能指标

(24)

式中：H(jω)为需要设计的前置滤波器;Tu(jω)为跟踪性能的上界;Tl(jω)为跟踪性能的下界。

选择跟踪性能的上下界分别如式(25)、式(26)所示。

(25)

(26)

所选择的跟踪性能的上下界，保证了满足该上下界的闭环系统阶跃响应，其超调量不超过5%、上升时间不超过1.5 s、调节时间不超过2.5 s，符合跟踪性能要求。

2.4 频率阵列选择与复合边界生成

选择对象模板具有较大不确定性的频率作为频率阵列的一部分，经观察选取的频率阵列为ω=[0.010.050.10.51510501005001 000]rad/s。

在所选频率阵列下，利用Matlab的QFT工具箱将对象模板根据鲁棒稳定性要求，在Nichols图上绘制鲁棒稳定性边界；同理，根据跟踪性能指标要求，在Nichols图上绘制跟踪性能边界。将各性能边界进行整合，得到的开环系统复合边界如图4所示。

图4 开环系统复合边界Fig.4 Open-loop system composite boundary

图4中，左右贯通的曲线为跟踪性能边界，非贯通的椭圆形曲线为鲁棒稳定性边界。系统满足性能指标要求的条件为：当开环系统频率响应曲线L0(jω)在低频处位于跟踪性能边界的上方，且与跟踪性能边界的距离越小越好；在高频处位于鲁棒稳定性边界椭圆外部，且不与鲁棒稳定性边界椭圆相交。

2.5 反馈控制器和前置滤波器确定

开环系统频率响应曲线如图5所示。

图5 开环系统频率响应曲线Fig.5 Open-loop system frequency response curves

由图5(a)可知，开环系统频率响应曲线L0(jω)与开环系统复合边界关系不符合要求，因此系统无法满足性能指标要求。

本文设计反馈控制器C(s)，以保证开环系统频率响应曲线L0(jω)在所选择的频率点处位于对应跟踪性能边界上方，且在高频处L0(jω)不与鲁棒稳定性边界相交。

(27)

设计QFT设计控制器后，开环系统频率响应曲线如图5(b)所示。开环系统频率响应曲线在所选择频率点处位于跟踪性能边界上方且与边界的距离很小，以保证系统在设计前置滤波器时能满足跟踪性能要求。在高频处，开环系统频率响应曲线没有与鲁棒稳定性边界相交，以保证系统的稳定性。

本文设计前置滤波器H(s)，使得闭环系统响应的包络线位于跟踪性能的包络线之间，从而保证系统满足跟踪性能要求。

(28)

闭环系统跟踪边界响应曲线如图6所示。

图6 闭环系统跟踪边界响应曲线Fig.6 Closed-loop system tracking boundary response curves

2.6 分析与设计验证

QFT采用近似选点的方法对控制系统进行设计，所以必须验证系统是否在所有频率都满足设计要求。本文利用Matlab的QFT工具箱分别对稳定裕度边界和跟踪性能包络进行分析。

通过QFT工具箱得到的稳定裕度响应曲线如图7所示。

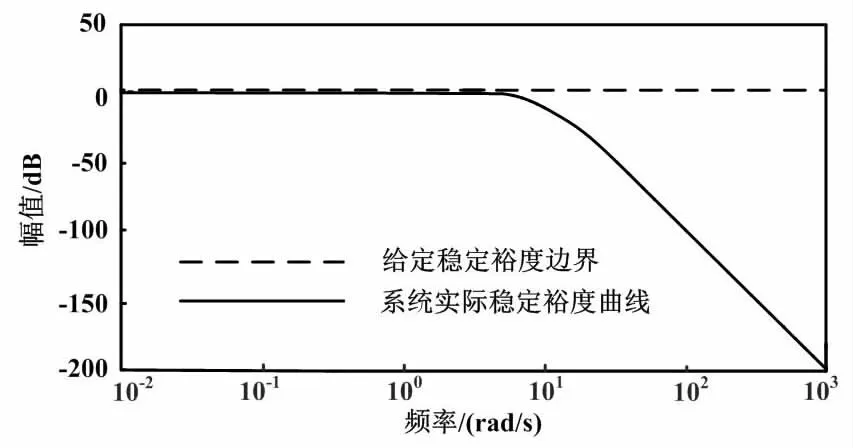
图7 稳定裕度响应曲线Fig.7 Stability margin response curves

由图7可知，系统实际稳定裕度曲线在所有频率点都始终位于给定稳定裕度边界的下方，而且没有超越给定边界的趋势，所以系统在所有频率点都满足稳定裕度要求。

通过QFT工具箱得到的闭环系统时域阶跃响应曲线如图8所示。

图8 闭环系统时域阶跃响应曲线Fig.8 Time-domain step response curves of closed-loop system

图8中，虚线为时域跟踪性能包络的上界和下界；实线是在考虑模型不确定性的情况下，所有对象模板的闭环时域阶跃响应曲线。由图8可知，采用QFT方法设计的气动调节阀控制系统满足系统动态性能要求。

3 仿真试验对比

为了验证所设计的反馈控制器和前置滤波器是否达到了预期设计标准，本文对系统进行仿真分析。利用Matlab的Simulink模块搭建了基于PID控制方法的气动调节阀控制系统和基于QFT控制方法的气动调节阀控制系统，将两者进行试验效果对比。

PID与QFT控制效果对比如图9所示。

图9 PID与QFT控制效果对比Fig.9 Comparison of control effects of PID and QFT

在标称状况下，给定阀位信号为20 mm时，基于PID与QFT控制方法效果对比如图9(a)中所示。在标称状况下，采用基于QFT控制方法，其系统无超调。而采用基于PID控制方法出现了一定的超调。因此，基于QFT控制方法在一定程度上优于基于PID控制方法。此外，采用基于QFT控制方法时，闭环系统满足设计过程中的各性能指标要求。

当气动薄膜式调节阀系统参数的变化在不确定设计范围内时，即阀门执行器内摩擦阻尼b=0.8 N/(mm/s)、弹簧的弹性系数k=8 N/mm情况下，其闭环阶跃响应曲线设计工况下基于PID与QFT控制方法效果对比如图9(b)中所示。在上述情形下，采用基于QFT控制方法的闭环阶跃响应曲线超调量小于5%、上升时间小于1.5 s、调节时间小于2.5 s，控制系统仍然满足系统的性能指标要求。而采用基于PID控制方法的闭环阶跃响应曲线其超调量远大于系统要求的5%，不再满足系统的性能指标要求。

基于QFT控制方法能够根据已知的系统不确定性条件，对控制系统进行设计。其对设计范围内的不确定性具有很强的鲁棒性。然而，在一些突发情况时，系统的不确定性将可能超出预先所设计的情况，而基于QFT控制方法的闭环系统仍然具有较强的鲁棒性。在阀门执行器内摩擦阻尼和弹簧的弹性系数持续减小的实际工况下，当参数减小到b=0.7 N/(mm/s)、k=7 N/mm时，系统的闭环阶跃响应曲线考虑情况外PID与QFT控制效果对比如图10所示。

图10 考虑情况外PID与QFT控制效果对比Fig.10 Comparison of the effects of PID and QFT outside the design conditions

基于PID控制方法的闭环阶跃响应曲线的超调量已达到38%，严重超过系统性能要求的5%，并且其调节时间也已超过2.5 s，严重超过系统的性能指标要求。基于QFT控制方法的闭环阶跃响应曲线，其超调量仍小于5%、上升时间仍小于1.5 s、调节时间仍小于2.5 s。由此可见，在基于QFT控制方法下，气动调节阀控制系统的性能指标仍符合设计要求。由上述分析可知，面对突发的极端工况，即系统的参数不确定性超出设计工况时，基于QFT控制方法仍具有较强的鲁棒性，由此显示出QFT的实际工程应用价值。

4 结论

针对气动调节阀控制系统在工业过程中不可避免地存在模型参数不确定性而影响系统控制效果的问题，本文提出了1种基于QFT的气动调节阀鲁棒控制策略。根据气动调节阀控制系统的性能指标要求，本文设计了基于QFT的鲁棒控制器。通过仿真研究，验证了本文所设计的控制器满足性能指标要求。相比于基于PID控制的气动调节阀控制系统，本文所设计的控制系统具有更强的鲁棒性和更优越的跟踪性能。