水轮机调节系统的动态滑模控制
付文龙,张仕海,郑 阳,卢启鹏,徐 潘
(1.三峡大学电气与新能源学院,湖北 宜昌 443002;2.武汉大学动力与机械学院,湖北 武汉 430072;3.三峡大学 梯级水电站运行与控制湖北省重点实验室,湖北 宜昌 443002)
0 引 言
近年来,电力系统的能源结构发生了巨大的变化[1]。这主要是由于一些可再生能源的快速发展,如风电、光伏发电、水电等,在能源供应中的比例日益增加[2]。由于风能和光能的间歇性和波动性使得电网的安全稳定运行受到了更多的挑战。水力发电机组作为电网中起调节作用的重要组成部分,为了使电网能够安全稳定运行,所以有必要研究水力发电机组的控制策略[3]。水轮机调节系统是水力发电机组的控制系统,根据功率输出设定值和转速设定值控制水轮机的转子转速以达到对电网输出功率的控制[4]。因此建立合适的水力发电机组模型和设计合适的控制策略至今仍是一个值得研究的问题。
在过去的几十年里,相关学者对水轮机调节系统的建模和控制方法进行了大量的研究。例如,郭文成等[5]建立了带调压井的水电站调速系统的数学模型,并对其稳定性进行了分析。杨建东等[6]对两种调节方式下的水电站调速系统建立了4个模型,并分析了简化模型对稳定性的影响。杨威嘉等[7]通过对抽水蓄能机组的建模、协同优化和运行评估的研究,提高了抽水蓄能机组的调节性能。
随着水轮机调节系统建模的发展,控制器的设计也得到了重大的改进。水电站的功率输出主要是通过改变水轮机的转速从而控制扭矩以达到对输出功率的控制。目前主要通过PID控制器对水电机组的输出功率进行控制。然而,水轮机具有非线性特性和不断变化的负荷使得传统的PID 控制面临巨大挑战。因此,为了提高水电机组的控制品质,近年来许多学者基于经典控制理论和现代控制理论开发了许多先进的控制方法,如模糊控制、预测控制和前馈控制[8]。许颜贺等[9]为了克服水泵水轮机’S’特性区域引起的空载启动条件下的转速振荡,运用模型预测和模糊控制理论,研究了抽水蓄能机组在低水头下空载启动的最优控制。王斌等[10]研究了一种用于时滞水轮机调节系统的模糊广义预测控制方法。陈帝伊等[11]研究了非线性水轮机调节系统的自适应输出反馈容错控制问题。虽然以上控制方法能够对非线性水轮机调节系统进行控制,但是不能保证系统具有鲁棒性。
滑模控制作为重要的鲁棒控制策略和非线性控制方法,在水电机组的运行控制领域受到广泛应用[12]。但是滑模控制的不连续性使得滑模控制在到达滑模面后,会在滑模面两侧出现高频、小幅度的抖振,而且水轮机调节系统中存在的时滞开关和系统惯性也会引起高频抖振,所以将滑模控制应用于水轮机调节系统的控制中也会存在抖振问题且一直没有得到解决。为了解决上述问题并提高水轮机调节系统的控制品质,本文以水轮机调节系统的非线性模型为基础,根据滑模控制理论,提出了动态滑模控制策略,设计了基于动态切换函数的动态滑模控制器;然后采用智能优化算法结合时间乘误差平方积分准则(ITSE)对设计的控制器参数进行了寻优;最后通过对比实验对设计的动态滑模控制器的有效性和控制性能进行了验证。仿真结果表明设计的动态滑模控制器显著的降低了系统中的抖振问题,并且能够有效的控制水电机组运行在稳定状态。
1 水轮机调节系统的非线性模型
具有超长引水隧洞的水轮机调节系统的结构框图见图1所示。由图1可以看出水轮机调节系统主要由控制系统和被控系统组成。整个系统可以通过压力管道、电液伺服系统、水轮机和发电机组的数学模型来构建[13]。建立了超长引水隧洞的水轮机调节系统[14]。
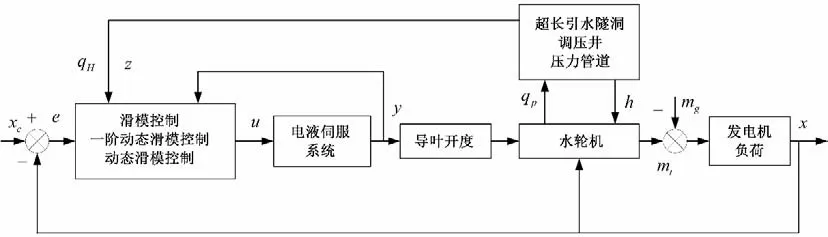
图1 水轮机调节系统结构图Fig.1 Structure diagram of hydraulic turbine governing system
超长引水隧洞的非线性动力学方程为[15]:
式中:TwH0为超长引水隧洞的水流惯性时间常数;z为调压室水位变化;hH0为超长引水隧洞的水头损失;H0为水轮机水头;qH为超长引水隧洞的流量。
调压室的动力学方程[16]:
式中:qP为压力管道的流量;TF为调压室的时间常数。
对于水轮机调节系统的动态性能和控制问题,假设水电站运行在额定工况,外部扰动为小扰动。具体而言,水轮机转速、水头和导叶开度的变化较小,而且水轮机的非线性特性较弱[17-19],所以将水轮机模型进行线性化建模。水轮机的力矩和流量方程[15]如式(3):
式中:eh,ex,ey表示水轮机的力矩传递系数;eqh,eqx,eqy表示水轮机的流量传递系数;mt为水轮机动力矩偏差相对值;x为水轮发电机组转速偏差相对值;y为导叶开度偏差相对值。
同步发电机的一阶方程如式(4)所示[20,21]:
式中:Ta为发电机组的惯性时间常数;mg为电网的负载扰动;eg为水轮发电机组的自我调整系数。
电液伺服机构作为水轮机的执行机构,用于放大控制信号,并提供足够的功率来控制导叶机构动作[22]。电液伺服系统的动力学方程如式(5)所示:
式中:Ty为伺服系统的时间常数;u是控制器输出。
基于上述数学模型可以建立水轮机调节系统的状态空间方程组为:
对于n阶非线性动力系统,为了便于控制器设计,水轮机调节系统的状态空间方程组可以转换为如下标准形式。
式中:X为系统的状态向量;A(X)、B是n维向量场;u是有限控制输出;Y是输出向量。X、A(X)、B和h(X)分别如下式所示:
式(7)的主要目的是找到理想轨迹xd的控制律,使得水轮机调节系统的输出跟踪理想轨迹,从而使跟踪误差xd-x趋于零。
2 水轮机调节系统的动态滑模控制策略
2.1 基于动态切换函数的水轮机调节系统动态滑模控制
动态滑模控制方法的主要思想是在滑模控制器和受控对象之间插入积分器。水轮机调节系统的动态滑模控制框图如图2所示。由于经过了积分器对高频抖振的过滤作用,实际受控对象的控制输入u就变得连续,从而减少了系统的抖振问题。这种动态滑模控制策略能够消除抖振并确保零稳态误差。
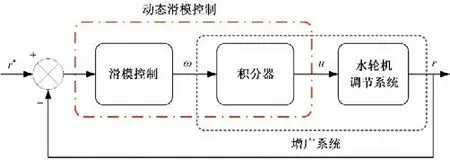
图2 水轮机调节系统的动态滑模控制框图Fig.2 Block diagram of dynamic sliding mode control for hydraulic turbine governing system
选择系统状态变量的跟踪误差为:
基于动态切换函数的动态滑模控制的切换函数为:
其中:
为了迫使系统尽快到达滑模面,选择指数趋近律如式(15)所示。
将式(13)两边同时对时间求导数为:
式中:
由于式(16)中不含有滑模控制律u,所以将式(6)中的第三项对时间求二阶导数可以得到状态变量x的三阶导数为:
将式(17)~(19)代入式(16),求得动态滑模控制器的控制律u如式(20):
式中:
采用李雅普诺夫稳定性进行系统稳定性检验,选择李雅普诺夫函数为V=s2∕2[27,28]。李雅普诺夫函数的导数为:由式(31)可知新的切换函数σ是渐进稳定的。当t→∞时,σ→0,系统能够在有效时间内到达滑模面σ=0。
2.2 水轮机调节系统的一阶动态滑模控制
针对一阶动态滑模控制,设计的切换函数与控制输入的一阶导数有关,新的切换函数为:
式中,c1<0,c2<0;c3>0。
同理,采用指数趋近律设计一阶动态滑模控制器,求得一阶动态滑模控制律u为:
式中:
由李雅普诺夫稳定性可知,设计的一阶动态滑模控制器能够使系统保持稳定运行。
3 滑模控制器的参数优化
对于控制器的设计,参数的设置也是控制器设计中的一个重要因素,因此,有必要对控制器的参数进行优化。参数优化需要对系统建立目标函数和选择适当的方法。传统上,工程师手动调整参数的调节时间过长且很难达到最优,所以有必要选择更为有效的方法。目前对参数优化的研究主要有智能优化算法和进化算法。进化算法由于其基于种群的搜索方法和并行特性,进化算法在工程中得到了广泛的应用[29,30]。
本研究采用PSOGWO 混合优化算法对水轮机调节系统进行滑模控制器参数优化的流程图如图3所示。

图3 基于PSOGWO算法的水轮机调节系统滑模控制参数优化流程图Fig.3 Flow diagram for optimization of slide mode control parameters of hydraulic turbine governing system by PSOGWO algorithm
设计的3 种滑模控制器都需要对参数寻优,因此对每个控制器使用相同的目标函数对控制器参数进行寻优。根据ITSE性能指标设计的系统控制器可以抑制过度过程中较大的偏差和过度过程时间。因此将ITSE 作为3 种控制器参数寻优的目标函数,并通过PSOGWO 优化算法寻优,然后通过寻优的参数进行仿真实验,以验证3种滑模控制策略对系统控制的有效性。
性能指标函数如式(38)所示:
4 仿真验证
在本节中,利用Matlab 软件对水轮机调节系统进行了仿真,并将设计的动态滑模控制器应用于控制系统的轨迹追踪。通过与常规滑模控制器的比较可以验证设计的控制器的有效性。系统(7)的参数如表1所示。

表1 水轮机调节系统的参数Tab.1 Parameters of the hydraulic turbine governing system
为了验证所设计的控制器的有效性和不丧失通用性的情况下,选择正弦信号和阶跃信号作为系统(7)中的输入信号。采用上节分析的ITSE 指标作为目标函数,并用PSOGWO 优化算法对三种滑模控制器进行参数寻优。3种控制策略分别在正弦信号和阶跃信号下的优化参数如表2、3和表4所示。

表2 动态滑模控制器的最优控制参数Tab.2 Optimal control parameters of dynamic sliding mode controller

表3 一阶动态滑模控制器的最优控制参数Tab.3 Optimal control parameters of first-order dynamic sliding mode controller

表4 滑模控制器的最优控制参数Tab.4 Optimal control parameters of sliding mode controller
3种控制器在正弦信号和阶跃信号下对系统输出的轨迹追踪曲线见图4至图6。从图4至图6可以看出3种滑模控制器对阶跃信号和正弦信号都可以很快追踪,没有出现明显的超调和振荡。设计的一阶动态滑模控制器和动态滑模控制器在水轮机调节系统的定点稳定中具有较短的过渡时间和相对稳定的暂态过程。由图4至图6的正弦信号的轨迹追踪曲线可以得出,利用设计的动态滑模控制器可以使系统稳定在选择的周期轨道上;而且设计的动态滑模控制器对水轮机调节系统在周期轨道跟踪下具有良好的动态响应。显然,水轮机调节系统的给定信号无论是阶跃信号还是正弦周期信号,所提出的动态滑模控制器都具有较好的跟踪能力和鲁棒性。

图4 不同给定信号下滑模控制的轨迹追踪曲线Fig.4 Trajectory tracking curves for sliding mode control with different given signals
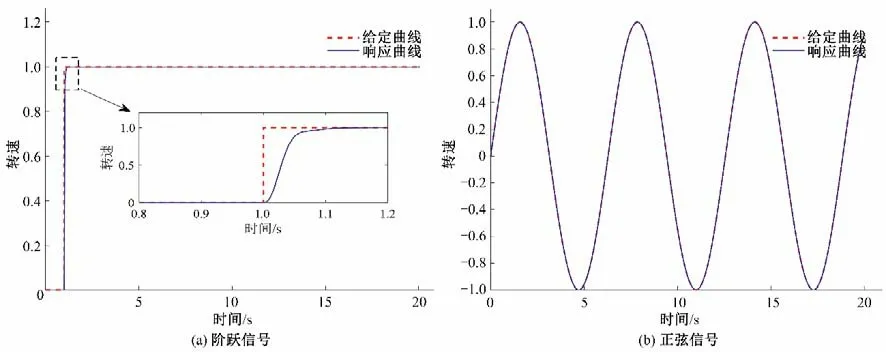
图5 不同给定信号下一阶动态滑模控制的轨迹追踪曲线Fig.5 Trajectory tracking curves for first-order dynamic sliding mode control with different given signals

图6 不同给定信号下动态滑模控制的轨迹追踪曲线Fig.6 Trajectory tracking curves for dynamic sliding mode control with different given signals
为了便于分析和比较3 种控制策略对系统的控制性能,进行了3 种控制器的对比实验。利用提出的动态滑模控制器,水轮机调节系统可以稳定到任意的固定点。假设固定点选择为xd=1(t),采用3种控制器来调整水轮机调节系统的响应。
从图7(a)可以看出,3种控制器都能在较短时间稳定,但是常规滑模控制器和一阶动态滑模控制器在固定点周围发生抖动,且抖动较为显著。由图8(a)可以看出,转速误差信号在稳定后,常规滑模控制和一阶动态滑模控制有很强的抖动并且误差变化较为显著。从图7(b)可以看出3 种控制器对正弦信号的轨迹追踪效果都很好,但是从图8(b)可以得出动态滑模控制器对水轮机调节系统的控制性能较好。因此,设计的动态滑模控制器能够对水轮机调节系统进行有效的控制,而且系统具有更好的动态响应。图9显示了3 种控制器在不同参考信号下的控制器输出曲线。由图9可以看到,常规滑模控制器和一阶动态滑模控制器出现了较为严重的抖振,但是动态滑模控制器的输出很平滑,没有出现抖振现象。上述分析表明动态滑模控制器不仅解决了常规滑模控制器设计时出现的抖振现象,而且对水轮机调节系统的控制效果十分优秀。
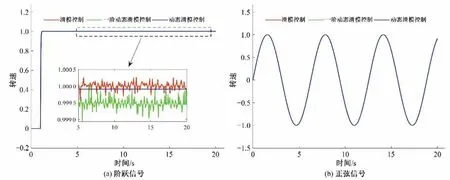
图7 3种控制器在不同参考信号下的轨迹追踪曲线Fig.7 Trajectory tracking curves of three controllers under different reference signals

图8 3种控制器在不同参考信号下的转速误差曲线Fig.8 Speed error curves of three controllers under different reference signals
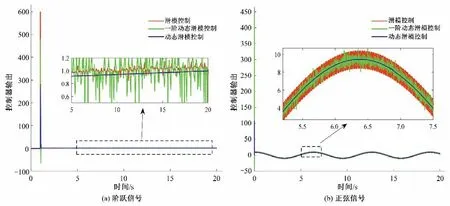
图9 3种控制器在不同参考信号下的控制器输出曲线Fig.9 Controller output curves of three controllers under different reference signals
5 结 论
本文设计了动态滑模控制器,用于水轮机调节系统的精确跟踪控制。在水轮机调节系统建模中,首先采用四阶微分方程来描述水轮机调节系统的非线性特性,然后使用动态滑模控制策略来建立控制律u和水轮机转速x之间的关系。基于仿真模型,将所提出的动态滑模控制器在不同参考信号下进行了比较。实验结果表明,所提出的动态滑模控制器不仅可以在不同给定信号下以较短的时间跟踪参考信号,而且提高了非线性水轮机调节系统的控制性能。此外,仿真结果也验证了动态滑模控制器相对于传统滑模控制器的优越性,并证实了动态滑模控制器可以有效降低滑模控制面临的抖振效应。

