考虑谷幅收缩变形的高拱坝多源信息融合安全评判

周心怡，胡 蕾，2，3，张启灵，2，3

(1.长江科学院 工程安全与灾害防治研究所，武汉 430010； 2.长江科学院 水利部水工程安全与病害防治工程技术研究中心，武汉 430010； 3.长江科学院 国家大坝安全工程技术研究中心，武汉 430010)

1 研究背景

谷幅收缩变形是水库左、右岸谷坡相同高程点之间最短水平距离的变化量，是区域变形在水平方向上的表现。200 m级以上特高拱坝一般建造在高山峡谷地带，地势险峻、高地应力的复杂特殊地形，使得坝址区的地质体在自然条件下就已经接近或达到了临界平衡的状态，而边坡的开挖和蓄水扰动又会破坏这种平衡，产生了两岸山体的收缩变形[1]。杨强等[2]认为裂隙水压力会改变岩体平衡，造成的塑性变形是蓄水过程谷幅收缩变形现象的原因。何柱等[3]指出蓄水对溪洛渡拱坝的谷幅收缩变形有影响，但更重要的原因是溪洛渡拱坝特殊的地质结构：从上游至下游层间、层内错动带渗透系数大。刘有志等[4]通过反馈仿真模拟，得出谷幅缩窄的主要原因是边坡开挖和蓄水对原有边坡形成扰动引起向下、向内的岩体蠕变变形。周志芳等[5]从渗流角度出发，得出谷幅收缩变形与溪洛渡水电站库区两岸有层状或似层状地层、透水层与相对隔水层互层分布的地质构造和水库蓄水有关。杨杰等[6]认为李家峡拱坝的谷幅收缩变形是库水压力渗透破坏岩体中断层、裂隙和破碎带，引起岩体的收缩变形所导致。国内外已有部分拱坝在运行过程中出现了谷幅变形的现象。意大利的Beauregard拱坝在河谷左侧边坡出现滑坡变形，蓄水以来谷幅收缩变形达100～200 mm[7-8]。瑞士的Zeuzier拱坝在经历河谷达到60 mm的横向收缩变形后，坝体上游面出现了多条裂缝，不得不进行修复[9-10]。法国Malpasset拱坝[11]、奥地利Kolnbrein拱坝[12]也在蓄水不久发生溃坝。我国已建成的小湾、锦屏一级、二滩、李家峡拱坝也在蓄水期或蓄水完成后由于水位上升观察到谷幅收缩变形的现象[13]。

坝体变形的监控模型已有诸多研究。胡江[14]引入徐变及其恢复项的时效变量表达式，代表谷幅收缩变形的能力，将水压、温度、失效分量应用增强回归树方法建立优化模型，得出各分量对坝体变形的影响。庄超等[15]建立了谷幅收缩变形反演及预测的解析模型，得出谷幅收缩变形与库水位的强关联性。本文拟建立坝体监控模型，研究谷幅收缩变形对拱坝变形的影响。

基于监测数据对大坝进行安全评价可以有效监测大坝运行安全情况，目前进行大坝安全评价主要采用基于单个或多个测点监测数据的监控模型，包括统计模型、确定性模型和混合模型[16]，目前常用的评价方法有模糊综合评价法、层次分析法、遗传神经网络模型、回归分析法等[17-19]。上述监控模型大多针对同一类型的监测数据，普遍描述“非此即彼”的确定性问题且存在评判时主观性过强的缺陷。而大坝是一个工作条件和环境均非常复杂的系统，受水文气象、地质条件、筑坝材料、体型尺寸等多个因素的影响，需要将大坝多源监测信息进行融合，从整体上综合分析评判大坝的安全运行状态。考虑到大坝的监测信息也具有不确定性，大坝安全状态及其评价指标的评语集“正常”、“基本正常”与“轻度异常”等之间存在一个模糊的渐变过程。鉴于上述方法均存在一定的局限性，难以反映评价体系的复杂性，本文引入D-S证据理论，充分利用其处理不确定信息的优势，同时为充分利用监测数据，采用云模型方法来确定大坝安全评判指标基本概率的分配，以增强评价结论的客观性。

本文以西南地区某高拱坝为例，拟建立坝体变形监控模型，研究坝体变形与谷幅收缩变形的关系；在此基础上引入谷幅收缩变形指标构建大坝安全多源信息融合评价指标体系，采用云模型和D-S证据理论融合大坝安全监测多源信息，建立大坝安全多源信息融合评判模型，以实现大坝安全状态的综合评判。

2 考虑谷幅收缩变形影响的大坝变形监控模型

我国西南地区某混凝土双曲拱坝坝顶高程610 m，最低建基面高程324.5 m，最大坝高285.5 m，自2013年水库蓄水以来，上下游均观测到较大的谷幅收缩变形，选取上游4条VDL01-VDR01至VDL04-VDR04、下游3条VDL05-VDR05至VDL07-VDR07共7条谷幅收缩变形测线绘制河谷变形和库水位变化图，见图1。

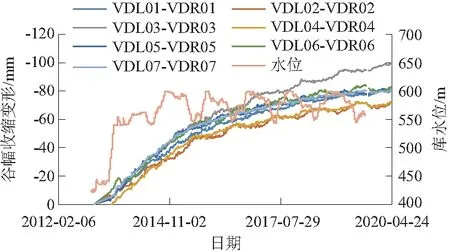
图1 谷幅收缩变形与上游库水位过程线Fig.1 Valley shrinkage deformation and upstream water level process lines

自蓄水以来，谷幅变形均表现为收缩变形状态，目前谷幅累计收缩变形达到了70～100 mm。从图1 中可知，以2015年为分界点，2015年之前蓄水初期谷幅收缩变形增速较大，谷幅收缩变形几乎成线性增长，之后平均变形速率逐渐放缓，趋于稳定，但谷幅收缩变形的绝对值仍在不断增长。

取左岸5#坝段、10#坝段、15#坝段垂线和上游水位作为分析对象，如图2。

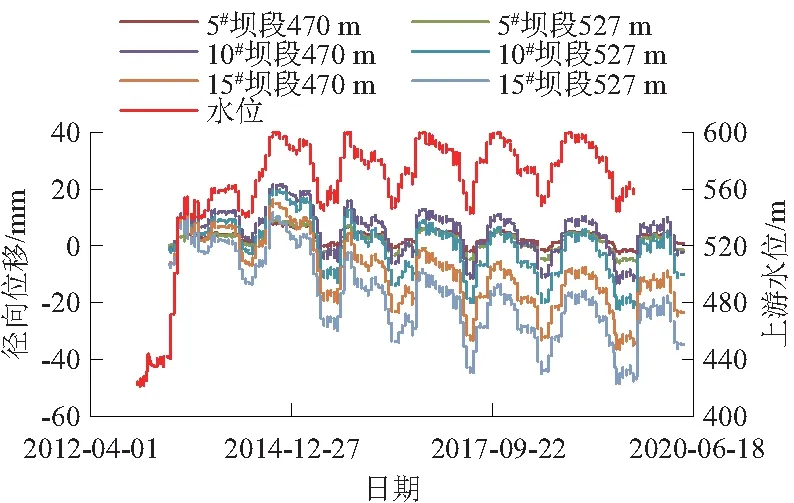
图2 径向位移与上游水位过程线(位移指向下游为正)Fig.2 Radial displacement and upstream water level process lines

在图2上游水位涨起和回落的5个蓄水周期中，各个坝段径向位移的变化规律相同，均随上游水位上升而增加、上游水位下降而减小，可见坝体径向位移与上游水位具有良好的相关性，但需要注意的是，自变形以来，坝体变形存在明显的倾向上游变形的趋势。

根据现有的相关研究，大坝任一点的变形可分为水压分量、温度分量和时效分量3部分[20]。水压分量可采用H、H2、H3的线性组合(H为上游水位)来表示；混凝土温度受气温影响随季节呈周期性变化，可选用多周期的简谐波作为因子；时效分量反映混凝土和岩基的徐变、塑性变形以及岩基地质构造的压缩变形，是随时间不可逆的变化，与时间呈曲线关系，一般可采用I1=ln(1+θ)，I2=1-e-θ，I3=θ，I4=θ2，I5=θ2，I6=1/(1+e-θ)来表示(Ii为时效分量，θ为观测日期距离基准值日期的天数除以100)，因而时效分量可表示为

(1)

如图1，谷幅收缩变形呈曲线变化，将时效分量组合对谷幅收缩变形进行拟合，采用最小二乘法得R2=0.985。拟合图见图3，可见时效分量可较好地表现谷幅收缩变形。

图3 时效分量拟合的谷幅收缩变形过程线Fig.3 Valley shrinkage deformation process line fitted by time-dependent component

变形效应量与3个分量之间的联系表达式为

(2)

式中：a1、a2、a3、a4为水压分量拟合系数；b1、b2为温度分量拟合系数；C为回归常数。

选取15#坝段垂线测点在2014年7月4日至2020年3月30日的径向位移监测数据为样本，共949组数据。采用逐步回归法得到各分量的回归系数和回归常数，建模结果如下，即

0.434θ+1.147ln(1+θ)-2 。

(3)

R2值为0.919，意味着水压分量、温度分量、时效分量可以解释径向位移的91.9%变化原因，模型通过F检验，说明模型有效。各变形分量的过程线见图4。

由拟合模型可知，径向位移受温度变形分量影响较小，与运行期混凝土温度较稳定的情况相吻合。坝体变形主要受水压分量和时效分量两部分影响。由图4可知，水压变形分量自蓄水以来均指向下游，时效变形分量均指向上游，自蓄水以来一直在持续增大，当时效变形分量对坝体造成的影响超过了水压变形分量对坝体造成的影响时，坝体将出现倾向上游的变形趋势。由于时效分量具有较好的表达谷幅收缩变形的能力，主要反映了谷幅收缩变形的变化规律，推测谷幅收缩变形可能是坝体倾向上游变形的主要原因。考虑到谷幅收缩变形对大坝运行状态的上述重要影响，下文将谷幅收缩变形作为大坝安全评价的指标之一。

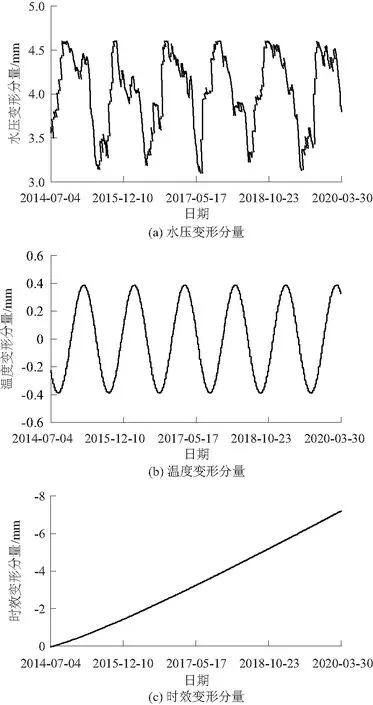
图4 变形分量过程线Fig.4 Component process lines of deformation

3 基于云模型和D-S证据理论的大坝安全多源信息融合评判模型

云模型是针对概率论和模糊数学在分析不确定性的不足上，描述某个具有定性的概念与其数值表示之间的一种不确定性的转换模型，构成一种定性与定量间的相互映射，云模型的数字特征包括期望值Ex、熵En和超熵He。D-S证据理论是在充分考虑了决策不确定性基础上，根据这些证据建立一个可信度的初始分配，由D-S证据理论中各个证据结合准则，计算得出它们共同作用对每个命题的支持程度。在多个证据融合过程中基本可信度分配概率函数的获得和权重的分配是建立D-S证据理论模型的基础，也是研究难点，现有文献中多采用专家评分法或经验确定，主观因素影响较大，由云模型求得的隶属度能克服传统方法主观性过强的缺点，熵权法确定的各指标权重结合隶属度得到基本可信度分配，最后用D-S证据理论融合各个指标基本可信度分配得到整个系统的可信度分配值。该模型建立步骤如下[21-24]。

步骤二：计算云模型的数字特征期望值、熵和超熵，即

(4)

式中：Ex、En、He分别为云模型的3个数字特征期望值、熵和超熵；Heij=s，s为常数，根据评语本身情况进行调整。

步骤三：利用云模型确定底层指标基本可信度赋值。选取q个云滴对应于各安全等级的隶属度求和取均值作为各个评价指标在相应安全等级下的隶属度，即

(5)

(6)

(7)

(8)

式中：μij为该评价指标相应于各安全等级的隶属度；xk为监测指标的监测值；Exij、Enij、sij是第j个评价等级云模型的3个数字特征期望值、熵和超熵；βi(Hl)为修正后的底层指标基本可信度赋值。

步骤四：确定各指标权重。

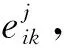
(9)

(10)

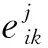
(11)

(12)

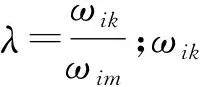
用D-S证据理论融合各个评价指标的基本可信度分配：

(13)

(14)

由D-S证据理论结合准则可将各指标基本可信度融合得到整个系统在评语集上的基本可信度[25-26]。

(15)

(16)

(17)

4 工程实例

上文中的混凝土双曲拱坝布置了较为完善的监测系统，在选取安全评价指标时考虑到指标应具有的全面性、代表性、客观性和监测指标数据的易获取性的特点，通过查阅书籍和文献拟定的大坝安全评价指标体系见图5[27]。

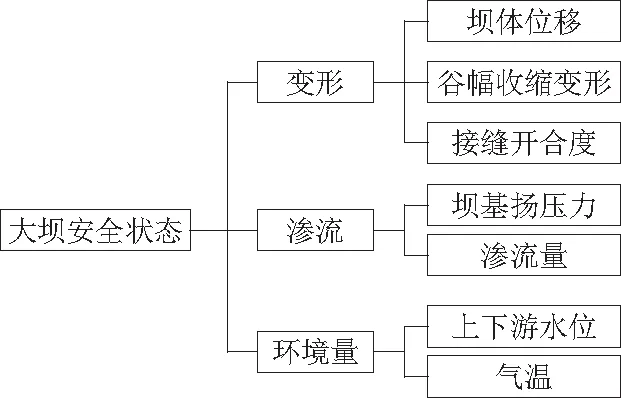
图5 大坝安全评价指标体系Fig.5 Dam safety monitoring and evaluation system

(1)建立大坝安全等级评价的评语集H={H1，H2，H3，H4}={正常，基本正常，轻度异常，重度异常}(HN+1情况劣于HN情况)。

(2)从变形、渗流和环境量3个方面选取了7个监测指标，以及各指标相应安全等级的取值范围，详见表1。扬压力的指标参考《混凝土拱坝设计规范》(DL/T 5346—2006)、《混凝土坝安全监测资料整编规程》(DL/T 5209—2020)等规范及相关设计文件确定，水平位移、谷幅收缩变形的指标参考了已有的数值计算和监测分析成果(资料源于《金沙江溪洛渡水电站混凝土拱坝工作性态及谷幅收缩影响分析专题报告》)，其余不宜采用规范或设计参考值的物理量，利用其监测资料的历史极值(最大值、最小值)采用统计方法(小概率法)确定。其中坝体水平位移指标选取坝体径向位移；坝基扬压力指标选取排水幕后的渗压系数，可以反映帷幕的防渗效果；气温指标选取实际气温和年平均气温14 ℃的差值。

表1 大坝安全评价指标体系及标准Table 1 Index system and standard of dam safety evaluation

(3)由式(4)可得拟定的7个评价指标对应4个安全等级的云模型如表2。

表2 大坝安全评价指标云模型参数Table 2 Cloud Model parameters of dam safety evaluation index

(4)每个安全评价指标随机选取500个符合各安全等级标准的实测值，由式(5)—式(8)得到底层指标基本可信度分配值如表3。

表3 大坝安全评价底层指标基本可信度分配Table 3 Basic credibility distribution of bottom indices of dam safety evaluation

(5)根据熵权法计算各底层指标的权重，由熵权法可得变形性态各评价指标(U11、U12、U13)的权重分别为0.82、0.10、0.08；渗流性态各评价指标(U21、U22)的权重分别为0.67、0.33；环境量各评价指标(U31、U32)的权重分别为0.45、0.55。

(6)根据Dempster证据合成法则，由式(9)—式(17) 可得到各子系统指标中各底层指标的基本可信度分配综合值，最终得到整个系统的可信度分配综合值，详见表4。

表4 大坝安全评价指标基本可信度分配Table 4 Basic credibility distribution of dam safety evaluation indices

由表4可知，按照最大隶属度原则，“基本正常”可信度最大，因此可以认为该大坝处于“基本正常”状态。该水电站自2013年蓄水以来，在荷载和外部环境的作用下，未出现明显的异常现象，整体上呈现正常状态，模型评判结果与实际情况基本相符，说明该模型合理可行。

5 结 论

(1)在分析监测数据规律的基础上，采用逐步回归法，通过坝体变形监控模型，建立了坝体变形与谷幅收缩变形的联系。监控模型结果表明谷幅收缩可能会引起坝体倾向上游变形，这与监测数据反映的规律基本一致，验证了监控模型的合理性和可靠性，谷幅变形是高拱坝进行安全评价不可忽略的影响因子。

(2)引入谷幅收缩变形指标，融合大坝多种监测指标信息，构建了云模型与D-S证据理论相结合的大坝安全多源信息融合安全评判模型来评判大坝的安全性，基于监测数据由云模型求得的隶属度来确定大坝安全评价指标基本概率分配的方法，克服了传统方法主观性较强的缺点。熵权法确定的各指标权重结合隶属度得到基本可信度分配，D-S证据理论融合各指标基本可信度分配得到整个系统的可信度分配值。模型评价融合结果表明，该大坝处于“基本正常”状态，与该高拱坝的实际情况基本相符，验证了该模型的合理性。