动态信息素更新和路径奖惩的蚁群算法

马世轩，游晓明，刘 升

1.上海工程技术大学 电子电气工程学院，上海 201620

2.上海工程技术大学 管理学院，上海 201620

旅行商问题（traveling salesman problem，TSP）有如下定义：假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。在本文中，假设计算两个城市之间的距离的方式都使用欧氏距离，并假设所有城市坐标都处于同一个平面之中。本文只讨论对称TSP问题，即从点i到点j的距离和从点j到点i的距离是相同的。

旅行商问题是生活中问题的抽象的重要的模型，其基本特点是易于描述，难于求解，是典型的NP 难（nondeterministic polynomial hard）问题。因此，对旅行商问题的研究具有重要意义。目前解决TSP 问题的方法主要有暴力穷举法、贪心算法、分支定解算法、动态规划算法、遗传算法、蚁群算法、模拟退火算法、粒子群算法、Hopfield 神经网络算法等。近几年不断有新的更高效的智能优化算法被提出：如张九龙等[1]对蝴蝶优化算法（butterfly optimization algorithm，BOA）、飞蛾扑火算法（moth-flame optimization algorithm，MFO）、正弦余弦优化算法（sine cosine algorithm，SCA）、蝗虫优化算法（grasshopper optimization algorithm，GOA）、哈里斯鹰优化算法（Harris hawks optimizer，HHO）、麻雀搜索算法（sparrow search algorithm，SSA）进行了对比分析研究。也有相关文献[2]和[3]等对智能算法的应用做出了研究，研究表明蚁群算法有突出的表现。因此本文使用蚁群算法来研究TSP问题。

蚁群算法的提出：1991年，Dorigo[4]受到蚂蚁觅食行为的启发，提出了蚂蚁系统（ant system，AS）并用于解决TSP 问题。AS 算法模拟自然界中蚂蚁的交流方式，比如信息素的释放与信息素的挥发。这两种策略增强了AS 算法的正反馈性能，最优解上会被释放更多的信息素，同时其他解的路径上信息素会随着迭代次数的增加而缓慢挥发。由于蚂蚁更倾向于信息素浓度高的路径，故该路径被选择的概率也会增加，这种此消彼长的方式极大加快了算法收敛速度，提高算法收敛性；禁忌表的加入使蚂蚁无法经过已经通过的城市，避免算法产生不必要的时间复杂度，提高算法在TSP 等NP 难问题中的求解效率[5]。1997年，Dorigo等[6]提出蚁群系统（ant colony system，ACS），将局部信息素更新与全局信息素更新相结合，隐性控制信息素上下限，改善算法的性能，对算法易陷入局部最优的问题进行了改良。2000年，Stützle 等人在蚁群优化算法（ant colony optimization，ACO）的基础上提出MMAS（max-min ant system）[7]，是目前为止解决TSP和QAP（quadratic assignment problem）等组合优化问题最好的一类ACO 算法[8]。上述传统算法能有效解决小规模TSP问题，但是难以解决大规模问题。很多学者对传统算法进行各种改进。

1999 年，Bullnheimer 等[9]所提出的等级蚂蚁系统（rand based ant system，RAS）是精英策略的另一种应用，在信息素更新环节中只使用了精英蚂蚁[10]。张松灿等提出单种群自适应异构蚁群算法的机器人路径规划[11]和基于蚁群算法的移动机器人路径规划研究[12]。代婷婷等提出改进的蚁群算法在路径规划问题中的应用[13]和蚁群算法的改进及其在最优路径中的应用[14]。赵静等[15]提出基于改进蚁群算法的移动机器人路径规划。顾军华等[16]提出基于改进蚁群算法的多机器人路径规划研究。陈银燕等[17]提出机器人导航路径的多种群博弈蚁群规划策略。李涛等[18]提出基于进化蚁群算法的移动机器人路径优化。孙宇翔等[19]提出基于精英策略的蚁群算法在AGV（automated guided vehicle）路径优化中的应用。李维维等[20]提出栅格环境下机器人导航路径的双种群蚁群规划。游晓明等[21]提出一种动态搜索策略的蚁群算法及其在机器人路径规划中的应用。Karakostas 等[22]提出一种求解旅行商问题的双自适应广义变量邻域搜索算法（double-adaptive general variable neighborhood search，DA-GVNS）。朱宏伟等[5]提出基于动态反馈机制的双种群蚁群算法的研究应用（pearson correlation coefficient ant colony optimization，PCCACO）。陈佳等提出基于自适应分级机制的多种群蚁群算法（EDHACO）[23]和结合信息熵的多种群博弈蚁群算法（WAS）[10]。马飞宇等[24]提出基于异构双种群全局视野蚁群算法的移动机器人路径规划。

上述现代算法虽然性能有了改进，但是在解决大规模TSP 问题时，解的精度和收敛速度有待进一步提高。在近期研究中，常规蚁群算法存在运行效率低、算法停滞和易陷入局部最优等不足，容易出现死锁问题，收敛速度慢，效率较低，容易陷入局部最优，运算时间过长，求解精度不高，难以解决大规模问题，为了提高多样性和搜索效率和质量，使得路径更加平滑，针对这些问题，本文提出了动态信息素更新和路径奖惩的蚁群算法。

本文的主要工作是针对蚁群算法容易陷入局部最优，收敛速度慢，难以解决大规模问题的情况，在前人的研究基础上，提出基于收敛系数的动态信息素更新策略和基于最优路径集合的奖惩策略的蚁群算法和三种局部优化方法。依据信息熵和停滞次数的动态信息素的更新策略和基于最优路径集合的奖惩策略的蚁群算法，在动态信息素更新策略中，利用收敛系数来动态调节信息素，从而有效地平衡算法的多样性和收敛性。在搜索过程中，通过持续提高收敛系数，加快了收敛速度；当信息熵降低或者停滞次数达到一定数值时，通过降低收敛系数，从而跳出局部最优；同时基于最优路径集合，对较优路径奖励，对其他路径惩罚，从而减少蚂蚁每一步可选城市的数量，减少计算量，加快收敛速度。

1 相关工作

1.1 蚁群系统

为了解决AS 易于陷入局部最优以及停滞的问题，Dorigo 等[6]在其基础上又提出蚁群系统（ACS），它成为蚁群算法当中改进效果最好的算法之一，给研究人员很大的启迪，给整个蚁群算法带来了深远的影响。

1.1.1 启发式信息

设启发式信息为η(i,j)，d(i,j)为两个城市i和j之间的欧氏距离，则η(i,j)如式（1）所示：

1.1.2 路径构造函数

在AS中，结合启发式信息，Dorigo将信息素因子与启发式信息结合，引入到城市的选择环节中，如式（2）所示：

式中，Pij表示城市i到城市j的转移概率，τij代表了从城市i到城市j的信息素浓度，ηij则是城市之间的启发式信息，allowedk是蚂蚁在城市i时可供选择的城市集（在TSP问题中，城市只可被访问一次，allowedk为还没有被访问的城市）。α和β分别指代信息素和启发式的影响程度。

在ACS中，通过式（3）进行路径构建：

式中，s代表将要被选择的下一城市，S表示通过AS算法中式（2）的方式进行解的构建，q是由算法随机生成的数，q0是一个定常数，且q0∈[0,1],allowedk代表可选的城市集，即还没有被经过的城市集。

1.1.3 局部信息素更新

ACS引入局部信息素更新策略，用于制约与平衡全局信息素更新策略，增加非最 优路径的被选择概率。蚂蚁每走一步就会对信息素实时更新，所经过路径上的信息素 将依照式（4）进行改变：

式中，∂表示局部信息素挥发率，τ0代表初始信息素量，值为,Lnn是根据贪婪法则（每次进行下一城市选择时，选择最近的城市点）得到的路径长度，而n则是当前测试集的城市数。由此可知，在初始阶段τ0是个远小于Δτij的值，它们之间至少有n倍的差距。

1.1.4 全局信息素更新

在ACS模型中只更新属于最好路径的各条边的信息素浓度。

除了局部信息素更新外，ACS还通过全局信息素的更新方式增加最优解被选择的概率，如式（5）和式（6）所示：

式中，ρ为全局信息素挥发率，Δτij为每次迭代信息素增量，Lgb为当前最优路径长度。ACS的全局信息素更新策略，即在最优路径释放信息素，使全局最优解对以后迭代蚂蚁的路径构建成正反馈作用，增加整个算法的收敛速度。

1.2 信息熵

1948年，Shannon在他著名的《通信的数学原理》论文中指出：“信息是用来消除随机不确定性的东西”，并提出了“信息熵”的概念，来解决信息的度量问题。

对于任意一个随机变量X，它的信息熵H(X)定义如下：

式中，p(x)代表随机事件x的概率。

1.3 k-opt

k-opt局部搜索算法也称k交换算法。k-opt的基本原理是应用局部搜索的概念，通过对k条边（弧）进行交换，在初始解的邻域中对初始解进行调整，接受得到改进的可行解。一次最多可以找到的新可行解的个数为2k。设T是一条初始路径，该算法总是试图找到2个有序集合X(X∈T)和Y(Y∈T)，如果在一定要求下用Y集合代替X集合，使得新的费用代价变小，则这k条边的交换就被称为k-opt 交换。优化解X就叫作T的kopt优化解。

举例当k=3 时，可能得到如图1 所示的8 条k-opt的新路径。

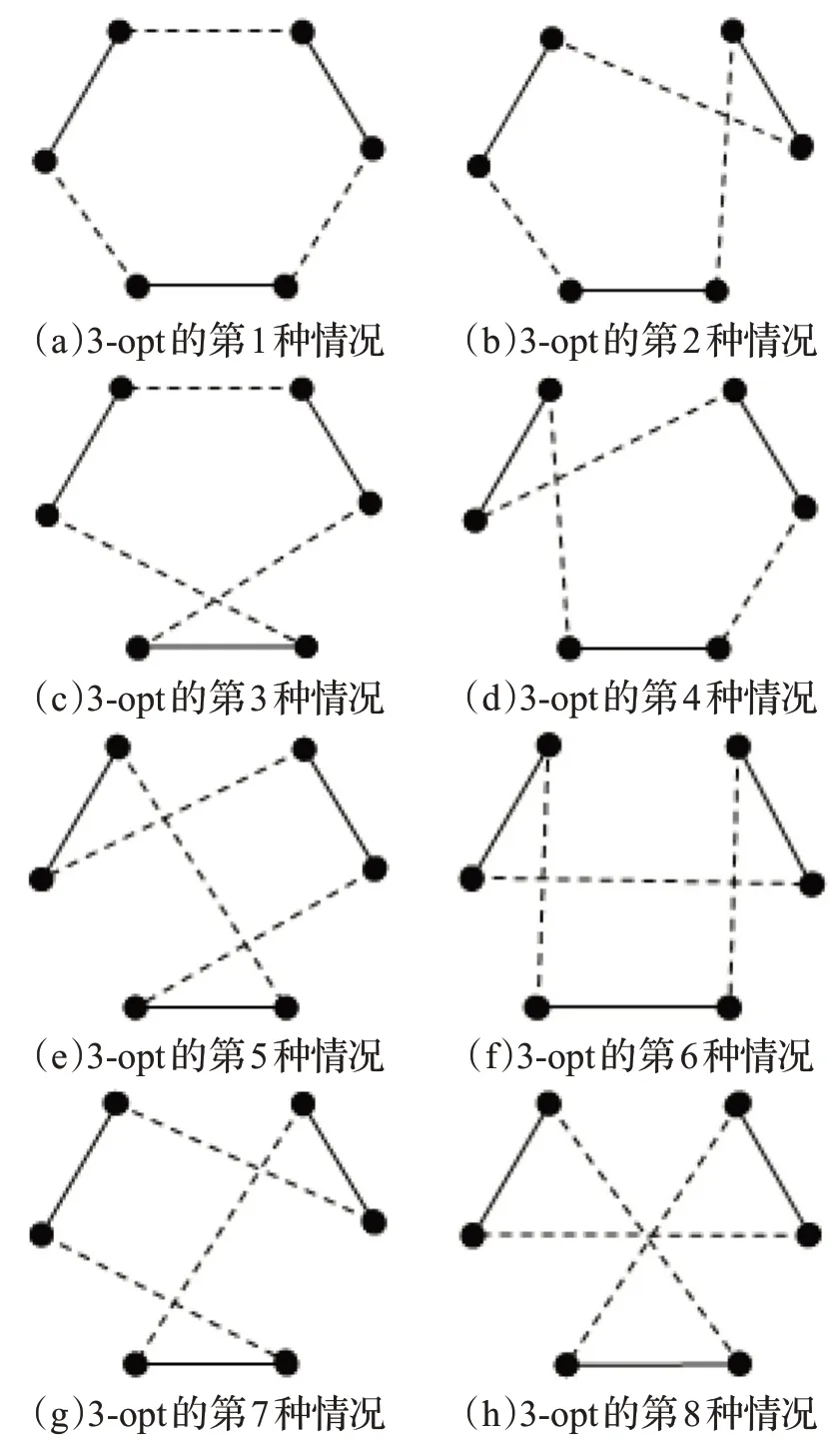
图1 3-opt优化Fig.1 3-opt optimization

2 本文算法改进

2.1 基于收敛系数的动态信息素更新策略

2.1.1 相对信息熵

设种群相对信息熵为PRIE（population relative information entropy）。

信息熵体现的是未知事物的信息量，基本参数是概率，且概率分布越平均，信息熵越大。在蚂蚁总数量确定的情况下，越多的蚂蚁得到不同解，则得解概率越平均。当每只蚂蚁都得到一个独立解时，信息熵最大[10]。信息熵越大，则多样性越好，反之越差。

设一批路径的数量为M，路径中不重复的路径个数为Nnr,c(xi)表示不重复路径xi在所有路径中出现的次数。

每轮迭代结束后按照式（9）、（10）更新PRIE：

由于TSP问题解是环路，在计算信息熵时将环路按照同一起点重新排列后相同的路径视为同一条路径。

由于对称TSP问题不在乎路径正反顺序，在计算信息熵时将正序相同和反序相同的路径视为同一条路径。

2.1.2 多样性增加系数

设多样性增加系数为CDI（coefficient of diversity increase）。

每轮迭代结束后按照式（11）、（12）更新CDI：

2.1.3 停滞次数

设停滞轮数为NS（number of stagnation）。

初始时，NS(0)=0。

每轮迭代结束后按照式（13）、（14）更新NS。

如果一轮搜索中找到新的更优解，则：

否则：

设最大停滞次数MNS=20。

0≤NS≤MNS

2.1.4 收敛系数

设收敛系数为CC（convergence coefficient）。

初始时，CC(0)=1。

设收敛系数最小值CCmin=1

设收敛系数最大值CCmax=200

设收敛系数增长率CG=1.1。

CCmin≤CC≤CCmax

2.1.5 收敛系数和停滞次数更新规则

每轮迭代结束后按照式（15）～（19）更新CC和NS。

设Lib是当前一轮迭代之中的最优路径长度，Lnn为贪心算法的路径长度，相对信息熵因子为RIEF（Relative information entropy factor），取值为1。

如果CDI＞0，则：

如果NS＞MNS，则：

如果Lib≤Lnn，则：

否则：

2.1.6 动态信息素更新规则

设收敛系数为CC，可以通过调节CC来平衡收敛性和多样性。CC越大，则信息素之间的差距越大，收敛越快；CC越小，则信息素越均匀，多样性越高。

路径(i,j)上的信息素τ(i,j)按照式（20）、（21）计算，信息素可缓存，减少重复计算，每轮迭代完成后重新计算信息素。

设Lnn为贪心算法的路径长度，Tbh为最优路径的合集，Lr(k)为Tbh路径中第k条的长度，Sr为Tbh路径的总条数，T(k)为Tbh中第k条路径的线段集合。

设函数C(k,i,j)表示路径线段(i,j)是否存在于最优路径的合集的第k条路径之中。设需要更新的路径集合为Tupdate。如果收敛系数比之前增加了，则Tupdate为最优路径集合和此轮迭代的路径的合集（去除重复），如果收敛系数比之前减少了，则Tupdate为全部路径集合。收敛系数增加的次数大于减少的次数。

信息素可以用64 位浮点数表示，信息素可能太大。如果有信息素τ超过64 位浮点数最大范围，则在构建一条路径时，直接返回全局最优路径。这是很少出现的边界情况。

对于函数C(k,i,j)的性能优化，由于每轮迭代中查询次数（n2级别）远大于修改次数1次，故可以用缓存和哈希表进行性能优化。在每轮迭代完成后修改哈希表，在每一轮迭代中，把查询的时间复杂度从O(n3)降低到O(n2)，修改的时间复杂度为O(n)。

2.1.7 控制收敛系数和信息素的原则和影响分析

收敛系数增大的原则有：

（1）当迭代最优路径长度小于贪心路径长度时，以较慢速度提高收敛系数，更多地在这一可能找到较优路径的区域搜索。

（2）当迭代最优路径长度大于贪心路径长度时，以较快速度提高收敛系数，以免进行无用的搜索，离开比贪心路径更差的区域。

收敛系数减小的原则有：

（1）当停滞次数达到一定值时，可能进入了局部最优的区域，需要增加多样性，跳出这一区域，降低收敛系数。

（2）当信息熵降低时，表明搜索的路径更加集中了，多样性降低了，按照信息熵的大小降低收敛系数，信息熵越低，使得收敛系数越小。

当收敛系数不变时，影响信息素的因素有：

（1）在最优路径集合中的线段的信息素较大，不在最优路径集合中的路径线段的信息素较小。

（2）当前路径越优，则贪心路径长度与当前路径长度的比值越大，则信息素越大，反之亦然。

收敛系数的变化对信息素的影响有：

（1）在最优路径集合中与不在最优路径集合中的路径线段之间的信息素差距随着收敛系数增大而指数级增大。

（2）贪心路径长度与当前路径长度的比值的大小差距会被收敛系数按照指数级放大或缩小，收敛系数越大，这一差距就会越大。

（3）收敛系数越大，则越靠近最优的区域的信息素的最大值会变得更大，越远离最优区域的信息素的最小值会变得更小，使得搜索更容易靠近最优路径区域附近。

2.2 基于最优路径集合的奖惩策略

2.2.1 最优路径集合

设集合Topt为最优路径集合，保存所有路径中的最短的Mopt条路径。设集合Topt的大小为Mopt，取值为10。

（1）要求集合Topt不包含重复路径。

（2）当生成了一条新路径时，如果集合Topt中路径数量小于Mopt，则将这个新路径添加到Topt中。

（3）如果这条路径的长度比集合Topt中最差路径更长，则不添加此路径，否则使用此路径替换最差路径。

2.2.2 每一步的可选城市选择方法

设Topt为最优路径合集，设每个城市的路径邻居城市为Topt的路径中与当前城市相连的城市。每一步的可选城市由它的路径邻居城市和其他随机选择的城市组成，排除已经走过的城市。

每一步的可选城市数量最大为NCL,取值为40。

这样就可以缩小搜索范围，对最优路径集合进行奖励，对其他路径进行惩罚，减少蚂蚁每一步可选城市的数量，减少计算量，提高收敛速度。

每个城市的路径邻居城市可以缓存，每轮迭代完成后重新计算。

2.3 局部优化方法

2.3.1 k-opt

在本文中，设NC为城市数，k的随机选择范围是(NC/2≥k≥2)，当k越大，k被选中的概率越低。k被选中的权重为1/k。

2.3.2 k-exchange

k-exchange优化方法是指，先克隆原路径T得到路径X，在路径X中随机选择k个节点从路径X中删除，对于这k个节点重新随机排序后，放回路径X中删除的空位，构建新路径X。如果路径X的代价比路径T的代价更小，则使用路径X代替路径T。路径X称为路径T的k-exchange优化解。

在本文中，设NC为城市数，k的选择范围是(NC/2≥k≥2),当k越大，k被选中的概率越低。k被选中的权重为1/k。

举例，当k=2 时，可能得到如图2、图3所示的优化效果，使用图3代替图2，路径更短。

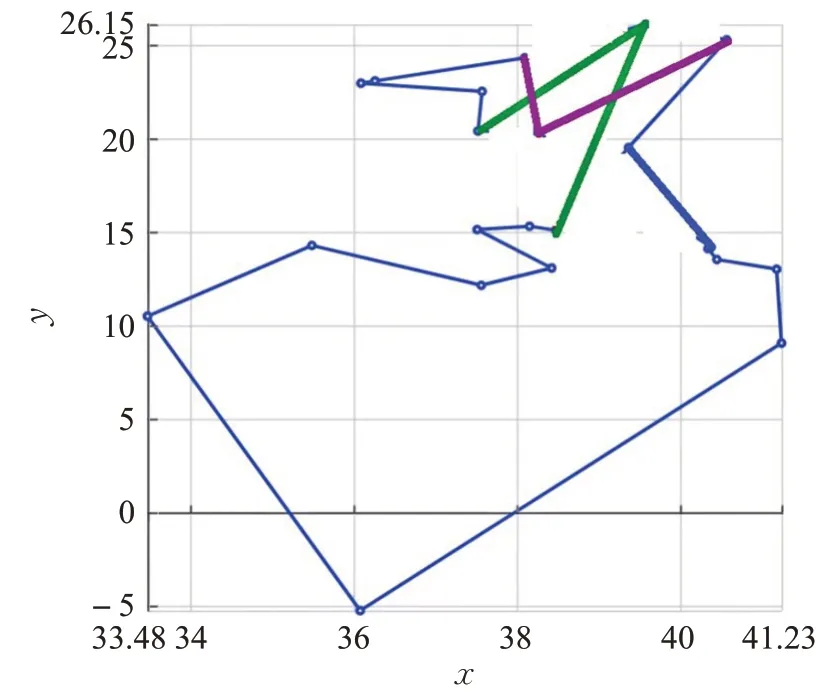
图2 2-exchange优化之前Fig.2 2-exchange before optimization

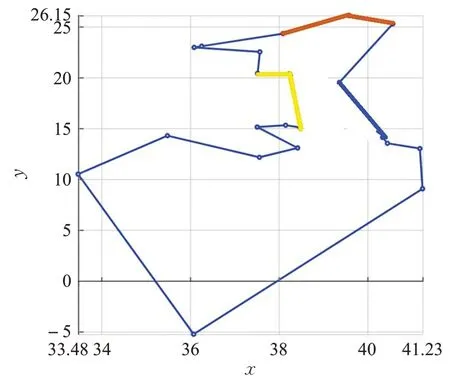
图3 2-exchange优化之后Fig.3 2-exchange after optimization

2.3.3 精准消除交叉点的2-opt

先从路径T的线段中每两条线段判断是否存在交叉点，找出这个交叉点的两个路径线段。如果存在交叉点，把交叉点的两条路径片段切断，使用2-opt优化生成新路径X，如果新路径X更短，则使用新路径X代替旧路径T。

因为查找交叉点的时间复杂度为O(n2)，所以要限制每次查找交叉点的线段条数最大为MCP，设MCP=40。

如图4、图5 所示，红色路径比原本的蓝色路径更短，因为三角形两边长度之和大于第三边长度，使用图5代替图4，路径更短。

图4 精准2-opt优化之前Fig.4 Precise 2-opt before optimization

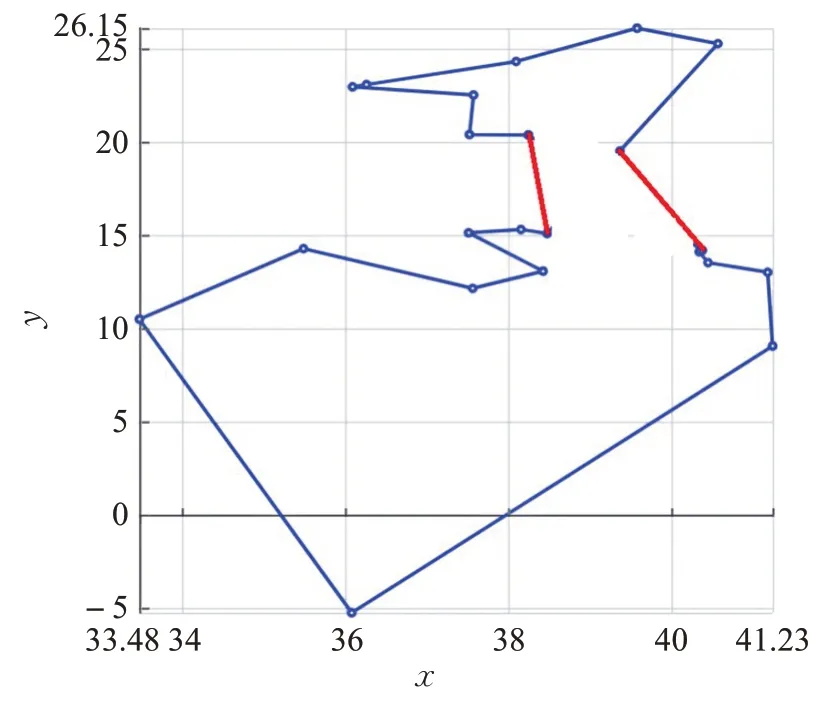
图5 精准2-opt优化之后Fig.5 Precise 2-opt after optimization

2.3.4 局部优化方法的使用

局部优化的路径选择方式为全局最优解和这轮路径中的长度排名靠前的路径，这些路径的局部优化有可能跳出局部最优，又不会太差，进一步提高解的精度。

在每轮迭代完成后，对全局最优解和这轮路径中的长度排名前一半的路径（去除重复）执行如下优化方法。

（1）对当前路径进行k-opt 局部优化，共生成10 条路径，使用更优解替代当前路径(2≤k≤N/2)。

（2）执行循环，使用k-exchange随机交换k个节点，使用更优解替代当前路径(2≤k≤N/2)，总共循环10次。

（3）执行循环，如果当前路径还有交叉点，则使用精准的2-opt局部优化消除交叉点，如果当前路径没有交叉点，随机生成一条k-opt路径取优化解，总共循环10次。

2.4 路径构建方式

2.4.1 贪心算法构建初始解

贪心算法的含义为每一步移动都选择当前代价最小的路径。使用贪心算法构建一条初始路径时，尝试随机选择一个起点构建一条路径。如果全局最优解未初始化，则将其作为全局最优解保存，记录此路径长度作为全局最短路径长度。

设贪心算法最多创建Mgreedy条路径，Mgreedy=20。

设贪心算法的每一步可选城市数最多为MCG=300 个。

2.4.2 状态转移概率

设蚂蚁从城市i移动到城市j的概率为P(i,j),蚂蚁从城市i移动到城市j的权重为w(i,j),节点随机选择概率为RSP（random selection probability）。

当蚂蚁在城市i，要选择下一个城市j时，先生成随机数p0(0＜p0＜1)。使用Allowed(k)表示当前可选的城市集合。当前可选的城市集合之中的城市数量为MA。然后使用轮盘法，根据P(i,j) 选出下一个城市j。蚂蚁从城市i移动到城市j，如式（22）～（24）所示。

启发式信息η(i,j)和ACS中式（1）相同。

权重可以用64位浮点数表示，使用轮盘法时，如果权重w超过64 位浮点数最大值，则直接返回权重最大的城市。这是很少出现的边界情况。

2.4.3 节点随机选择概率

设节点随机选择概率为RSP，多样性增加系数为CDI。

初始时，RSP(0)=0。

每轮搜索结束后按照式（25）更新节点随机选择概率RSP。

2.5 算法流程

（1）输入城市的坐标。

（2）初始化参数和最优路径集合。

（3）用贪心算法生成出Mgreedy条路径，计算出最短路径长度，初始化信息素，按照式（20）初始化每个城市的路径邻居城市。

（4）搜索轮数←0。循环执行步骤（5）到（7）。当搜索轮数到达最大迭代循环次数时，停止循环，输出最优路径及其长度，算法结束。

（5）设有Na只蚂蚁，每只蚂蚁使用状态转移概率构建路径或者按照概率进行节点随机选择构建出一条路径，如式（24）。

（6）在所有蚂蚁都构建路径完成后，搜索轮数增加1，对全局最优解和这轮路径中的长度排名前一半的路径（去除重复）执行三种局部优化方法。

（7）计算信息熵，按照式（10）计算多样性增加系数，按照式（12）计算节点随机选择的概率，按照式（25）更新收敛系数，更新停滞次数，按照式（15）～（19）更新信息素，按照式（20）更新每个城市的路径邻居城市和最优路径集合。

2.6 时间复杂度分析

设城市数为n，迭代次数为k，蚂蚁数为m，时间复杂度如表1所示。

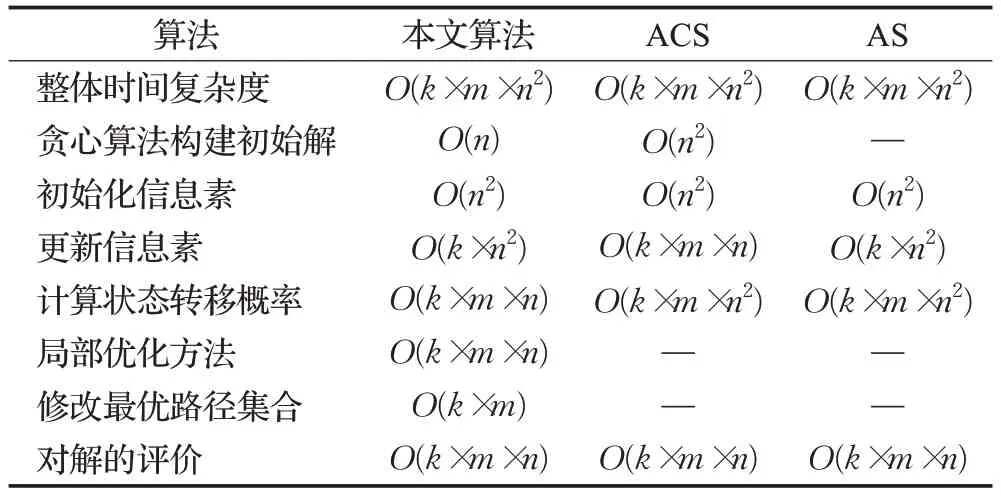
表1 时间复杂度Table 1 Time complexity

3 仿真实验测试与分析

3.1 参数设置

本文算法的默认参数如表2所示。

表2 本文算法的默认参数Table 2 Default parameters of algorithm in this paper

ACS的参数设置如表3所示。

表3 ACS算法的默认参数Table 3 Default parameters of ACS algorithm

3.2 算法性能测试

3.2.1 本文算法中策略和局部优化方法的测试

3.2.1.1 基于收敛系数的动态信息素更新策略性能测试

在ACS+三种局部优化方法基础上，保持其他策略和参数相同，在信息素方面，使用基于收敛系数的动态信息素更新策略与原本的ACS算法进行对比测试。

设算法A 为经典ACS，算法D 为ACS+基于收敛系数的动态信息素更新策略。设经典ACS算法花费的时间为1个单位。不同算法的平均每轮迭代时间如表4所示。不同算法总迭代次数相同的最优解和误差率如表5所示。

表4 算法A和算法D的平均每轮迭代时间Table 4 Average iteration time per round for Algorithm A and Algorithm D

表5 算法A和算法D的最优解和误差率Table 5 Optimal solutions and error rates for Algorithm A and Algorithm D

不同算法在测试算例Rand300中的相对信息熵、每轮平均路径长度和最优路径长度的变化曲线如图6、图7和图8所示。

从图6、图7、图8可以看出，得益于动态信息素更新策略，当信息熵降低时，导致平均路径长度和最优路径长度都减小，接近最优解；之后信息熵自动增加，导致平均解和局部最优解相应地变大，有助于跳出局部最优，从而可以自适应平衡多样性和收敛性。

图6 动态信息素更新与ACS的相对信息熵对比Fig.6 Comparison of relative information entropy between dynamic pheromone update and ACS

图7 动态信息素更新与ACS的迭代平均路径长度对比Fig.7 Comparison of iterative average path length between dynamic pheromone update and ACS

图8 动态信息素更新与ACS的最优路径长度对比Fig.8 Comparison of optimal path length between dynamic pheromone update and ACS

结果分析，使用了基于收敛系数的动态信息素更新策略之后，对于有些地图，比ACS 略差一点；对于有些地图，误差率大幅减少，大幅加快了收敛速度，提高了解的精度，规模越大效果越好。

例如，在Pr107 中，误差率从1.9%降低到1.1%；在Pr226中，误差率从2.8%降低到1.9%；在Rand300中，误差率从11.6%降低到7.5%。

因为动态的信息素能够自适应地调节多样性或者收敛性，所以规模越大，效果越明显，可以平衡解的精度和收敛速度的矛盾。

3.2.1.2 三种局部优化方法性能测试

在ACS算法基础上，保持其他策略和参数相同，使用与不使用三种局部优化方法进行对比测试。

设算法A 为经典ACS，算法B 为ACS+三种局部优化方法。设经典ACS 算法花费的时间为1 个单位。不同算法的平均每轮迭代时间如表6 所示。不同算法总时间相同的最优解和误差率如表7 所示。

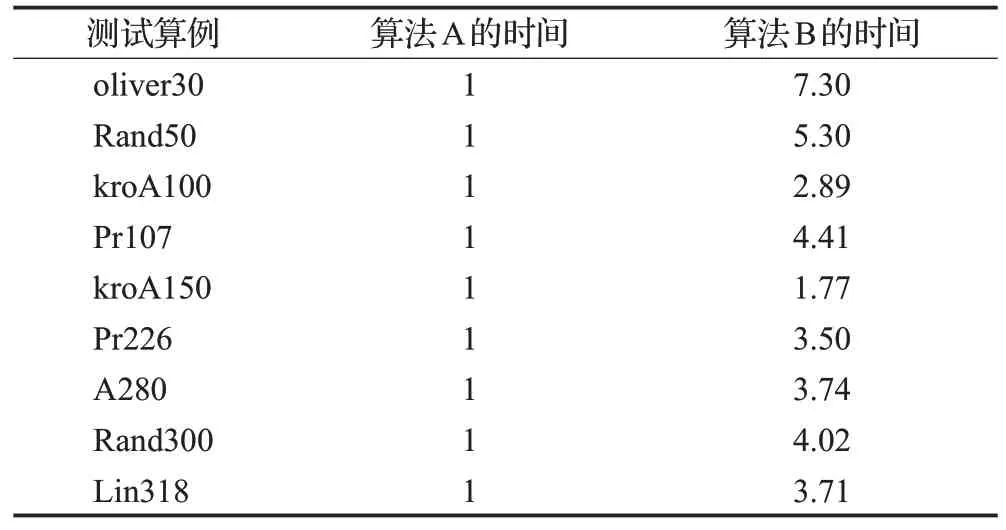
表6 算法A和算法B的平均每轮迭代时间Table 6 Average iteration time per round for Algorithm A and Algorithm B

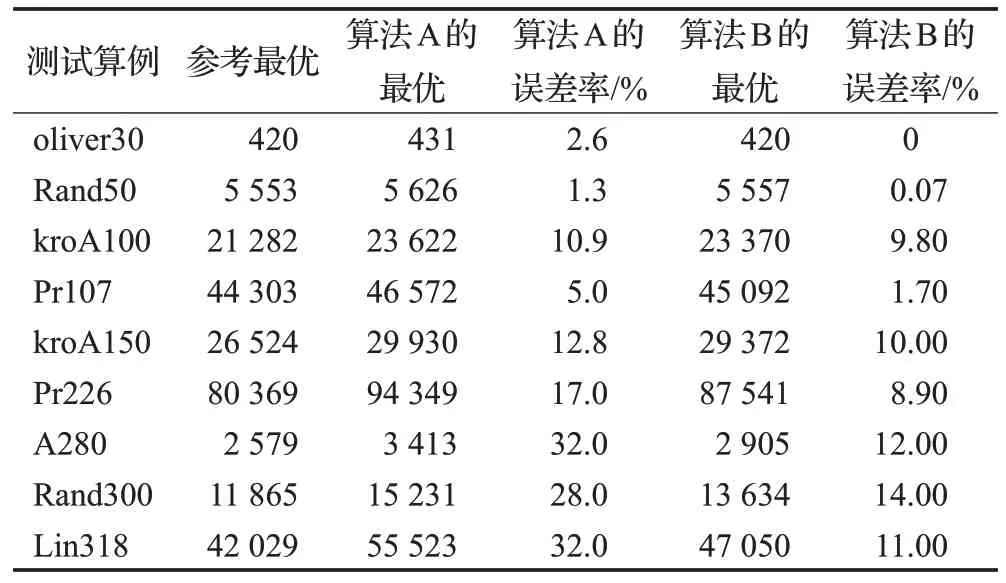
表7 算法A和算法B的最优解和误差率Table 7 Optimal solutions and error rates for Algorithm A and Algorithm B

不同算法在测试算例Pr226中的最优路径平面图和最优路径长度的变化曲线如图9、图10和图11所示。

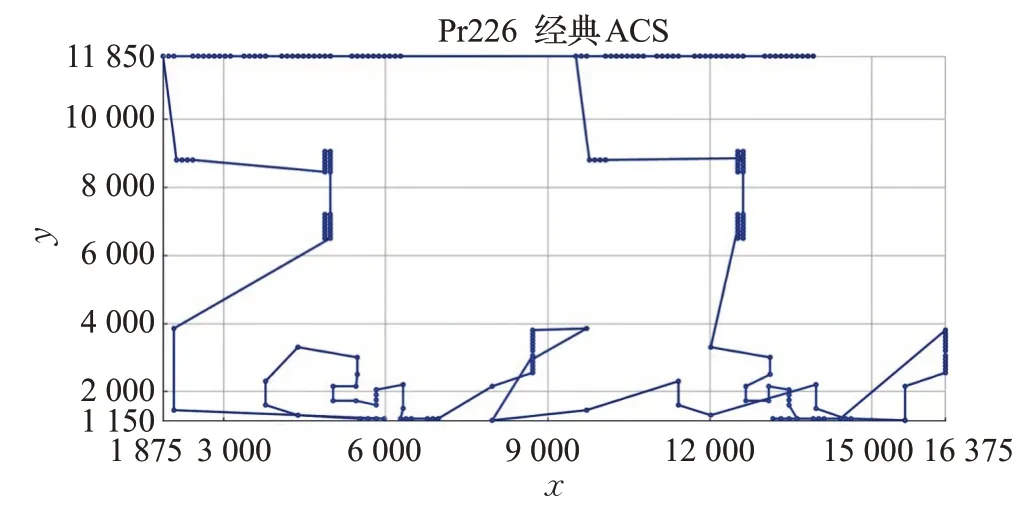
图9 Pr226中ACS的最优路径平面图（城市数：226，路径长度：94 349）Fig.9 Optimal path plan of ACS in Pr226

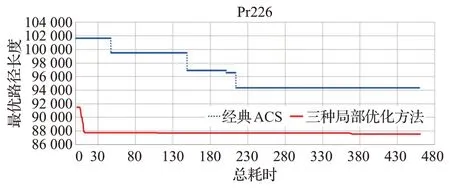
图11 三种局部优化方法与ACS的最优路径长度对比Fig.11 Comparison of optimal path length between three local optimization methods and ACS

结果分析，使用了三种局部优化方法之后，误差率大幅减少，大幅加快了收敛速度，提高了解的精度。

例如，在Pr107 中，使用了此策略后误差率从5.0%降低到1.7%；在Pr226 中，使用了此策略后误差率从17.0%降低到8.9%；在Lin318 中，使用了此策略后误差率从32%降低到11%。

三种局部优化方法因为增大了搜索空间，能够跳出局部最优，所以增加了多样性，进一步提高了解的精度。

3.2.1.3 基于最优路径集合的奖惩策略性能测试

在ACS+三种局部优化方法的基础上，保持其他策略和参数相同，在可选城市方面，使用基于最优路径集合的奖惩策略与原本的ACS算法进行对比测试。

设算法B 为ACS+三种局部优化方法，算法C 为ACS+三种局部优化方法+最优路径集合奖惩策略。设ACS+三种局部优化方法花费的时间为1个单位。不同算法的平均每轮迭代时间如表8 所示。不同算法总时间相同的最优解和误差率如表9所示。

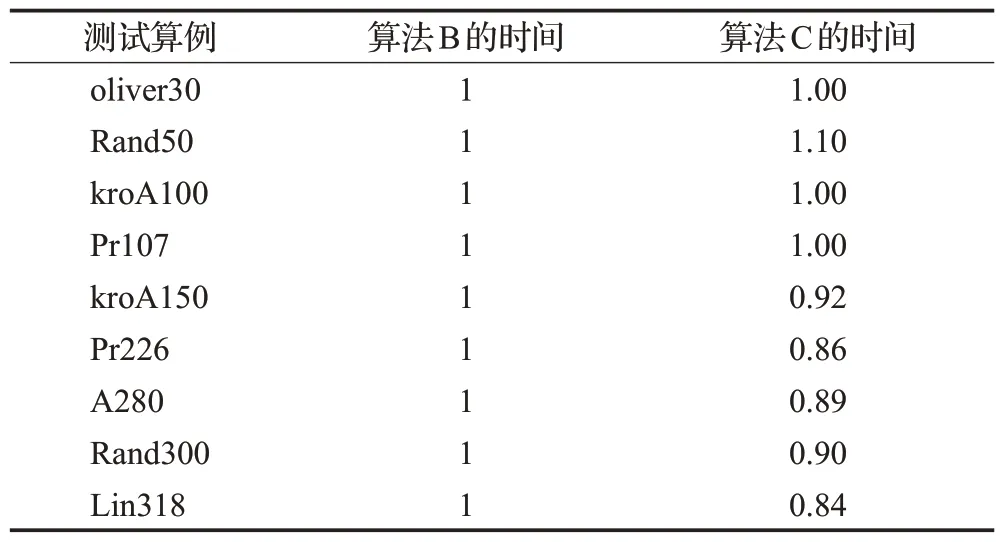
表8 算法C和算法B的平均每轮迭代时间Table 8 Average iteration time per round for Algorithm C and Algorithm B

表9 算法C和算法B的最优解和误差率Table 9 Optimal solutions and error rates for Algorithm C and Algorithm B

不同算法在测试算例A280 中的相对信息熵、迭代平均路径长度和最优路径长度的变化曲线如图12 和图13所示。

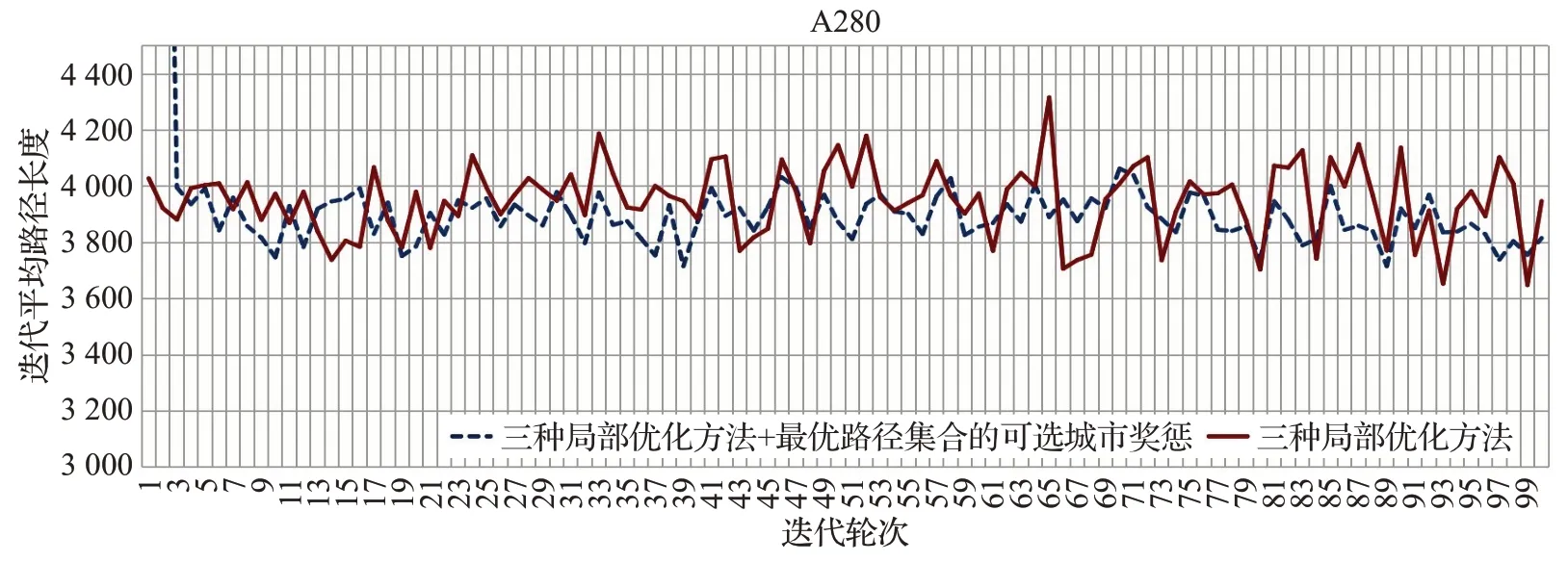
图12 有和无最优路径集合奖惩策略的平均路径长度对比Fig.12 Comparison of average path length with and without optimal path sets reward and punishment strategies

图13 有和无最优路径集合奖惩策略的最优路径长度对比Fig.13 Comparison of optimal path length with and without optimal path sets reward and punishment strategies

结果分析，使用了基于最优路径集合的奖惩策略之后，误差率大幅减少，大幅加快了收敛速度，提高了解的精度。规模越大，节省的计算量越大。

例如，在kroA100 中，使用了此策略后误差率从10.1%降低到5.9%；在kroA150中，使用了此策略后误差率从14.1%降低到12.0%；在A280 中，使用了此策略后误差率从23.8%降低到13.2%。

此策略因为缩小了搜索的范围，更接近最优解附近搜索，所以加快了收敛速度。

3.2.2 与传统算法和当今最新算法对比测试

3.2.2.1 对比算法的来源

EDHACO 来自于文献[23]；ACS 来自于文献[6]；MMAS 来自于文献[7]；WAS 来自于文献[10]；PCCACO来自于文献[5]；DA-GVNS来自于文献[22]。

3.2.2.2 对比算法的默认参数

PCCACO、EDHACO、WAS、DA-GVNS 的参数与原文献相同。ACS和MMAS的参数如表10所示。

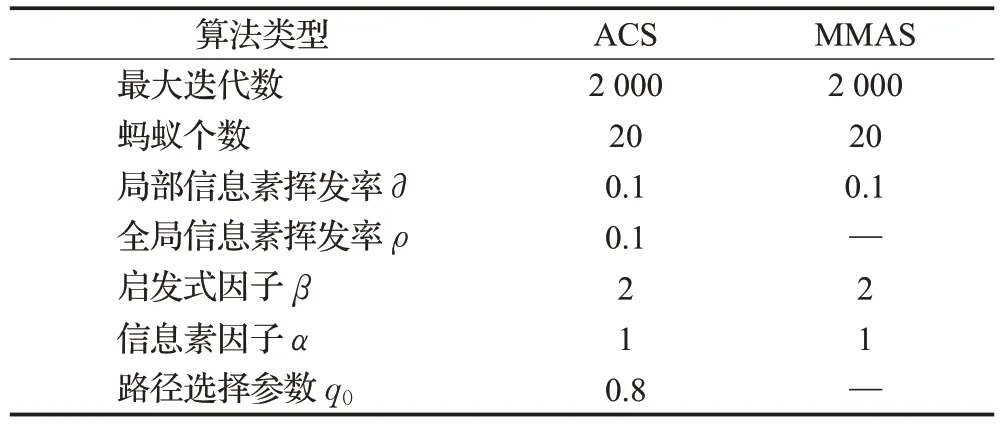
表10 ACS和MMAS的参数设置Table 10 Parameter settings for ACS and MMAS

3.2.2.3 在测试算例中的测试结果对比

测试结果对比如表11所示。由复杂度分析可以看出，本文算法没有增加时间复杂度。

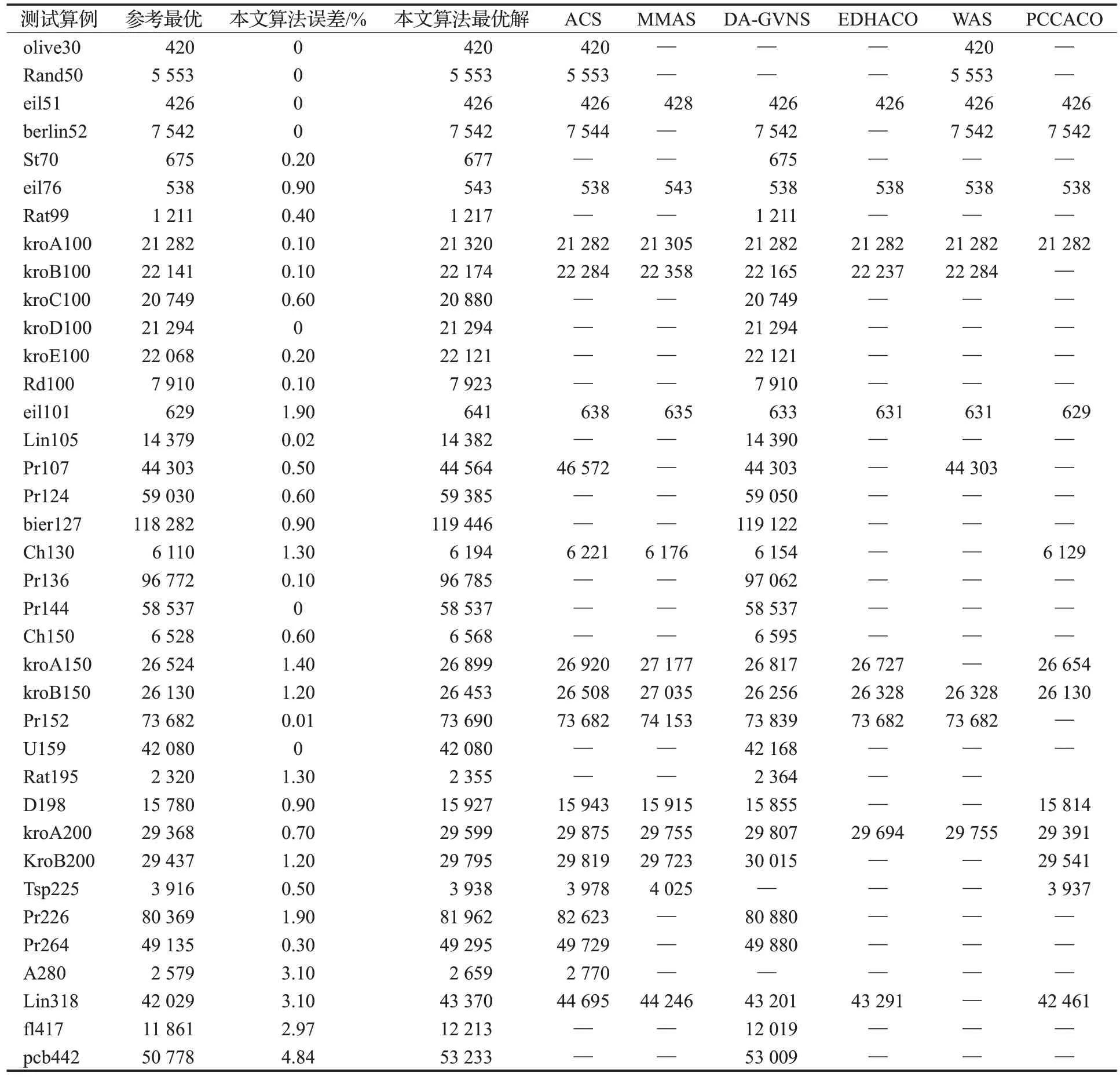
表11 本文算法与其他算法的测试结果对比Table 11 Comparison of test results of this paper algorithm and other algorithms

结果分析，本文算法比ACS、MMAS经典算法提高了解的精度，加快了收敛速度。

例如，在eil51中，本文算法与其他算法达到相同精度。在kroB100中，本文算法比经典算法MMAS提高很大，误差率从0.98%降低到0.1%。在kroA200 中，本文算法比ACS、MMAS经典算法对比，解的误差率0.7%优于1.7%和1.3%。在tsp225中，本文算法误差率0.5%，比ACS、MMAS 经典算法的误差率1.5%、2.7%，提高了很大的精度。在Pr264中，本文算法解的误差率0.3%优于ACS的误差率1.2%。

本文算法与近期的优秀算法相比精度很接近。例如，在kroB100中，本文算法比DA-GVNS的精度略低一点，差距在0.04%左右，也比EDHACO、WAS 有更高的精度，差距在0.28%左右。说明本文的策略对于小规模问题有效地平衡了精度和收敛速度的矛盾。

在kroA200 中，本文算法解的误差率0.7%，与DAGVNS、EDHACO、WAS 相比精度提高一些，差距在0.7%到0.3%左右，比PCCACO的精度略低一点，差距在0.7%左右。在tsp225 中，本文算法达到与PCCACO 几乎相同的误差率0.5%。在Pr264 中，本文算法误差率0.3%，与DA-GVNS 误差率1.5%对比，本文算法误差率优于DA-GVNS。说明本文的策略对于中规模问题有效地平衡了精度和收敛速度的矛盾。

在Lin318 中，本文算法解的误差率3.1%，与DAGVNS 对比很接近，相比差距在0.4%左右。在pcd442中，本文算法解的误差率4.8%，与DA-GVNS 对比很接近，相比差距在0.4%左右。说明本文的策略对于大规模问题有效地平衡了解的精度和收敛速度的矛盾。

综上所述，在不同规模的问题中，本文算法都能够有效地解决TSP问题。

3.3 最大停滞次数和相对信息熵因子的正交实验

最大停滞次数和相对信息熵因子会影响到收敛系数的降低。为了测试不同参数对于算法性能的影响，对这两个参数进行正交实验。

选择测试算例Pr264；最大停滞次数设定为4 个值15、20、25、30；相对信息熵因子设定为4 个值0.7、1.0、1.2、1.5；在相同的迭代次数300 代，其他参数相同情况下，总共16 组条件，各测试2 次取值，共32 次测试的最优解和误差率统计如表12所示，按照误差率排序。

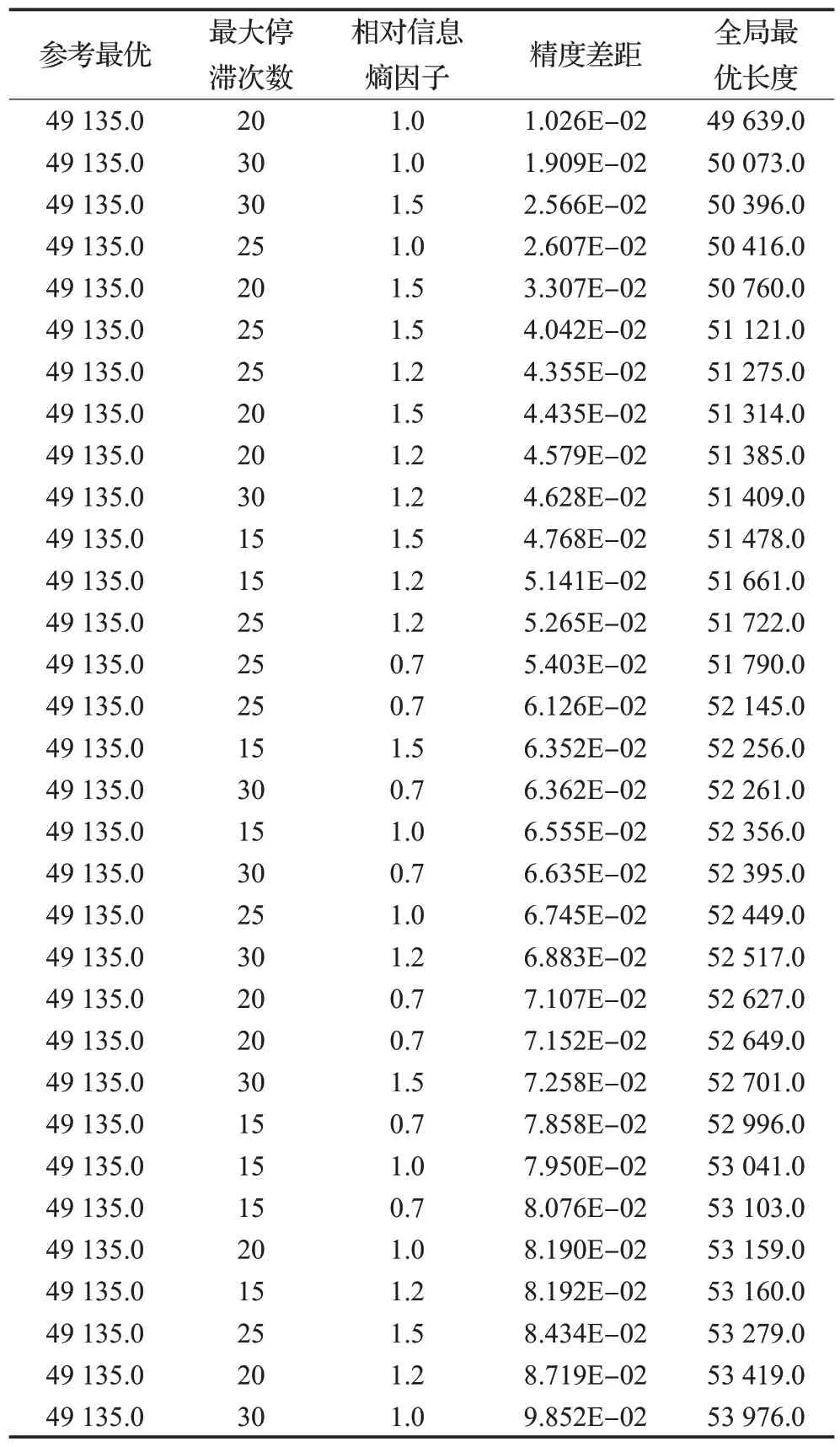
表12 最大停滞次数和相对信息熵因子的正交实验Table 12 Orthogonal experiment of maximum stagnation number and relative information entropy factor

从统计中可以看出，在排名前30%的测试结果中，最大停滞次数按照出现次数从大到小依次是20 出现4次，25出现3次，30出现2次；相对信息熵因子按照出现次数从大到小依次是1.5 出现4 次，1.0 出现3 次，1.2 出现2次。因此最大停滞次数的最合适区间为20到30；信息熵因子的最合适区间为1.0 到1.5。这证明了本文算法的参数设置是合理的。

4 结束语

针对常规蚁群算法容易陷入局部最优，收敛速度慢，难以解决大规模问题的情况，本文在前人的研究基础上，提出基于收敛系数的动态信息素更新策略和基于最优路径集合的奖惩策略的蚁群算法和三种局部优化方法。

经过实验测试，本文算法中，基于收敛系数的动态信息素更新策略和三种局部优化方法能够有效地平衡算法的多样性和收敛性，加快收敛速度，跳出局部最优；基于最优路径集合的奖惩策略能够减少计算量，缩小搜索范围，加快收敛速度，能够有效解决TSP问题，具有较高的求解效率。

以后的改进方向是使用多种群或者聚类策略，来进一步提高解决大规模问题的精度和收敛速度。