量表数据中不努力作答的识别和清理*

王 丹 刘红云

(北京师范大学心理学部,应用实验心理北京市重点实验室,心理学国家级实验教学示范中心[北京师范大学],北京 100875)

1 引言

量表调查是指通过制定详密的工具,要求被调查者据此进行回答以收集资料的方法。因其具有成本低、快捷高效和操作便捷等优点,被广泛应用于心理学、教育学和社会学研究。尽管研究者可以通过量表收集到大量有价值的数据,但是并不能保证作答者参与的热情和动机,如大量研究发现现实中作答率呈现逐年下降的趋势(Anseel,Lievens,Schollaert,& Choragwicka,2010;Christian,Dillman,& Smyth,2008;Weiner &Dalessio,2006)。特别是当下在线问卷的流行,很难保证在无人监管的情况下作答者认真参与调查(Pauszek,Sztybel,& Gibson,2017)。

不努力作答(Insufficient Effort Response,IER)又称不认真作答,指被调查者缺乏作答动机,作答不专心、疲劳或加速作答,导致作答数据无法反映其真实物质(Curran,2016;Hong,Stee dle,& Cheng,2020,Huang,Liu,& Bowling,2015;Meade &Craig,2012)。不努力作答的程度在2%到50%之间(Johnson,2005;Meade &Craig,2012),不努力作答更容易出现在题量较多的量表中,被调查者的疲劳效应会促使其在后半部分不认真作答(Berry et al.,1992;Clark,Gironda,& Young,2003)。被不努力作答污染的数据,不仅会令个体作答数据无效,还会为量表指标的计算带来偏差,得出不可靠的分析结果(Crede,2010;Johnson,2005;Huang,Curran,Keeney,Poposki,& DeShon,2012;Maniaci &Rogge,2014;McGonagle,Huang,& Walsh,2015;Merritt,2012;Steedle,Hong,& Cheng,2020;Woods,2006)。由此可知,对不努力作答的甄别就显得很有必要。

目前对不努力作答的主要甄别方法和指标大约有十几种,研究者主要集中在针对量表作答过程中可能出现的不努力作答的行为模式,构建不同的指标并评估指标甄别效果(Dunn,Heggestad,Shanock,& Theilgard,2018;Huang et al.,2012;Meade &Craig,2012)。面对不断出现的指标方法,如何选择和应用效果最好的指标成为了研究的重点。有研究通过模拟不同程度的不努力作答数据,评估在不同条件下,各指标的敏感度和特异性(Hong &Cheng,2019;Meade &Craig,2012)。但是,不努力作答表现多样,并非全是随机作答数据,有的还会呈现多种的规律,很难通过模拟数据研究得出的结论对实际测验中不努力作答情况进行推断。也有研究者以实际量表数据为分析对象,评估清除不努力作答数据后,工具质量指标的计算结果的变化(Steedle et al.,2019),但是并未对不同甄别指标在实际数据中的选择进行更进一步的研究。

综上,当前研究大多介绍不努力作答甄别的方法及其效果,而对于实际研究中如何综合应用多个指标进行甄别等问题缺少关注。本文在对不努力作答识别指标进行归纳的基础上,重点探索不同指标的适用性和一致性;并探讨了不努力作答的消极影响。最后,通过比较实际应用中清理不努力作答数据的不同方法,在方法选取方面给出了建议。

2 不努力作答识别方法概述

不努力作答的识别方法分为主动侦查法、作答过程指标法和指标分析法三类。主动侦查法是一种在测验实施之前,通过主动设置题目对不努力作答行为进行识别的方法,主要包括陷阱题、直接反应题和自评准确率。第二类是作答过程指标,基于计算机在线测试的普及,被调查者的作答过程信息可以被轻易获取,比如作答时间和作答完成率。第三类指标分析法是对不努力作答的一类事后甄别方法,该类方法通过计算已回收数据的各项指标,判断被调查者不努力作答的可能性,常用的指标有七种。详细见表1。

表1 不同IER模式所对应的行为表现及操作定义

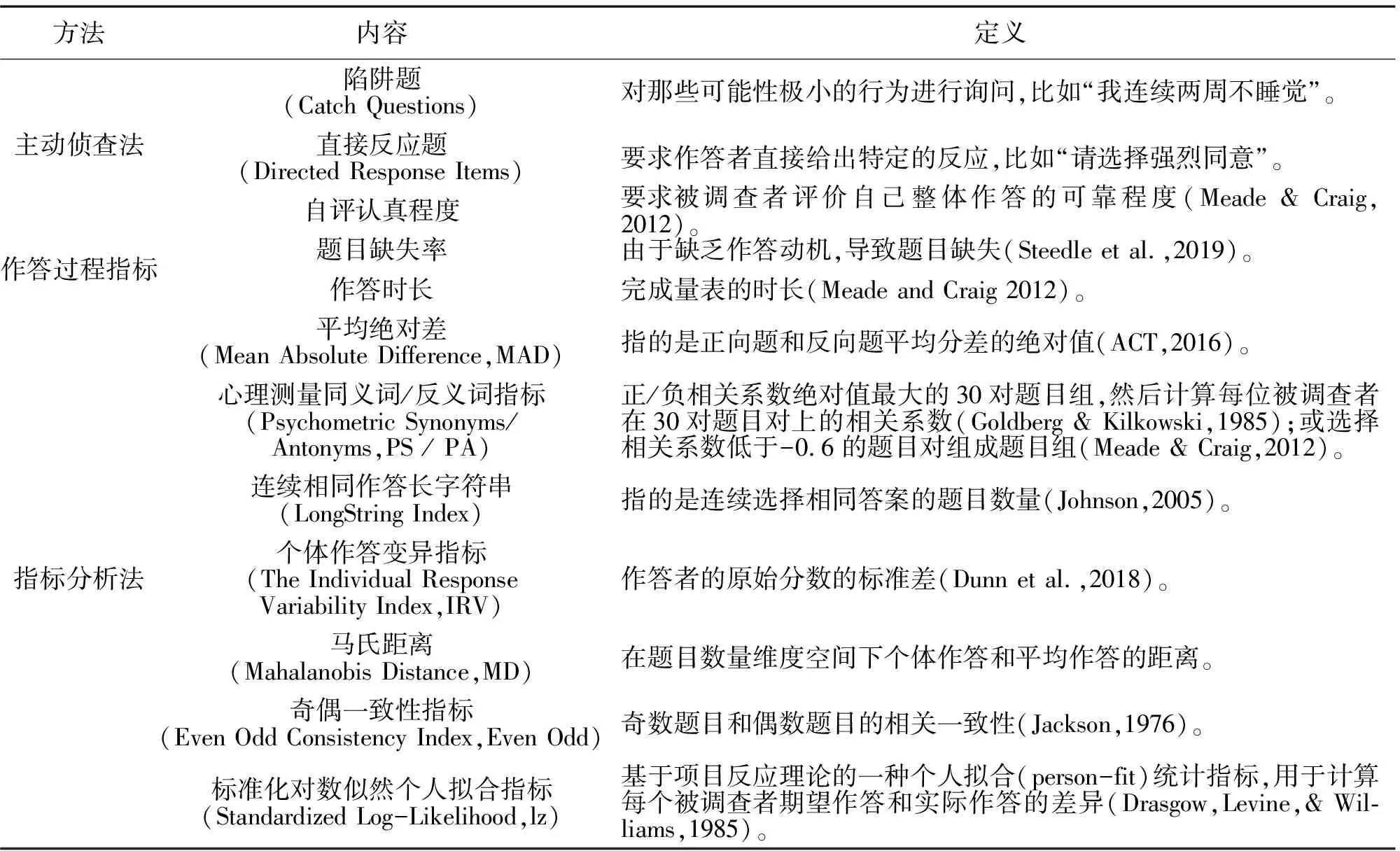
表1 不努力作答方法介绍

3 研究问题与设计

主要采用指标分析法,辅助主动侦查法和作答过程指标,探讨不同方法的应用情况。

3.1 研究方法

3.1.1 测验工具

通过一个实际的网络测试的量表数据,幽默风格量表(Humor Styles Questionnaire,HSQ),对不努力作答识别方法和效果进行研究。HSQ是由Martin等人开发的用于测试幽默类型的5点评分量表(Martin,Puhlik-Doris,Larsen,Gray,& Weir,2003),共有4个子量表,每个量表8道题目。

3.1.2 数据

所用的数据来自于心理测量项目公开的资源(https://openpsychometrics.org/_rawdata/)。1071名被调查者参与作答,其中男性581名,女性477名,缺失13人;年龄范围为14-70岁。在调查最后会询问被调查者作答准确率(Accuracy),即“请对自己作答的准确程度进行0至100的评分”。由于本量表为人格类型的测验,作答准确率和被调查者的能力无关,只和其作答的认真程度有关,因此被调查者汇报的准确率可等同于自评的认真程度。

3.2 指标截断值的确定

在进行指标识别之前,首先需要设置各指标的截断值(Cutoff)。对于主动侦查法和作答过程数据指标,并没有一个明确设置截断值的方法。这里将自评认真程度不高于50%的被判定为不努力作答;题目缺失率(Missing)可考虑采用缺失1道和2道题这两个标准来判定。

对于指标分析法中的多个指标,确定截断值的方法并不同(分析语句见https://osf.io/wgfhv/)。LongString的截断值采用Johnson(2005)提出的碎石图法,对所有作答者在每个选项上面不同长度的连续作答的频率进行比较,将碎石图的拐点作为截断值,每一个选项对应一个截断值。根据图1,选项2-4的拐点对应的题目数目为4,选项1和选项5的拐点在3或4,因此最终选出四组截断值,分别是(3,4,4,4,3),(3,4,4,4,4),(4,4,4,4,3)和(4,4,4,4,4)。

图1 选项1至选项5的碎石图

对于lz指标,可直接基于零假设的显著性检验,采用第一类错误率(α)0.01或0.05所对应的临界值作为截断值。利用R语言中的PerFit包(Tendeiro,Meijer,& Niessen,2016)计算每个被试四个子量表的lz值。参考Hong等(2020)的研究,当其中一个子量表的lz低于截断值时,意味着作答者的答案与预期答案的差异在统计上是显著的,代表其很可能没有认真读题或者随机作答,因此被判定为不努力作答。对于MD指标,理论上也可以采用零假设的显著性检验,但在实际中,MD的平方有可能偏离了中心卡方分布,直接采用此方法可能会带来较大偏差(Hong et al.,2020)。

对于MAD,PS,Even Odd、IRV和MD指标,截断值的确定主要有两种方法。第一种方法是异常值检测,该方法的原理是模拟各指标的零假设分布。首先通过清理数据降低IER的消极影响和α,然后选择合适的IRT模型拟合清理后的测验数据,再根据IRT参数和能力分布模拟样本作答,根据模拟样本计算出每个指标,并建立该指标零假设下的抽样分布,α=0.05和0.01对应的值为截断值(Steedle et al.,2019)。第二种方法比较简单,按照比例直接筛选不努力作答,比如Dunn等人以10%的比例筛选不努力作答被调查者(Dunn et al.,2018),Huang等人则分别以1%和5%设置截断值(Huang et al.,2012)。

这里采用第一种方法计算截断值,用R语言中的mirt包(Chalmers,2012)和careless包(Yentes &Wilhelm,2023),语句见附录1。各项指标的截断值和识别人数见表2。

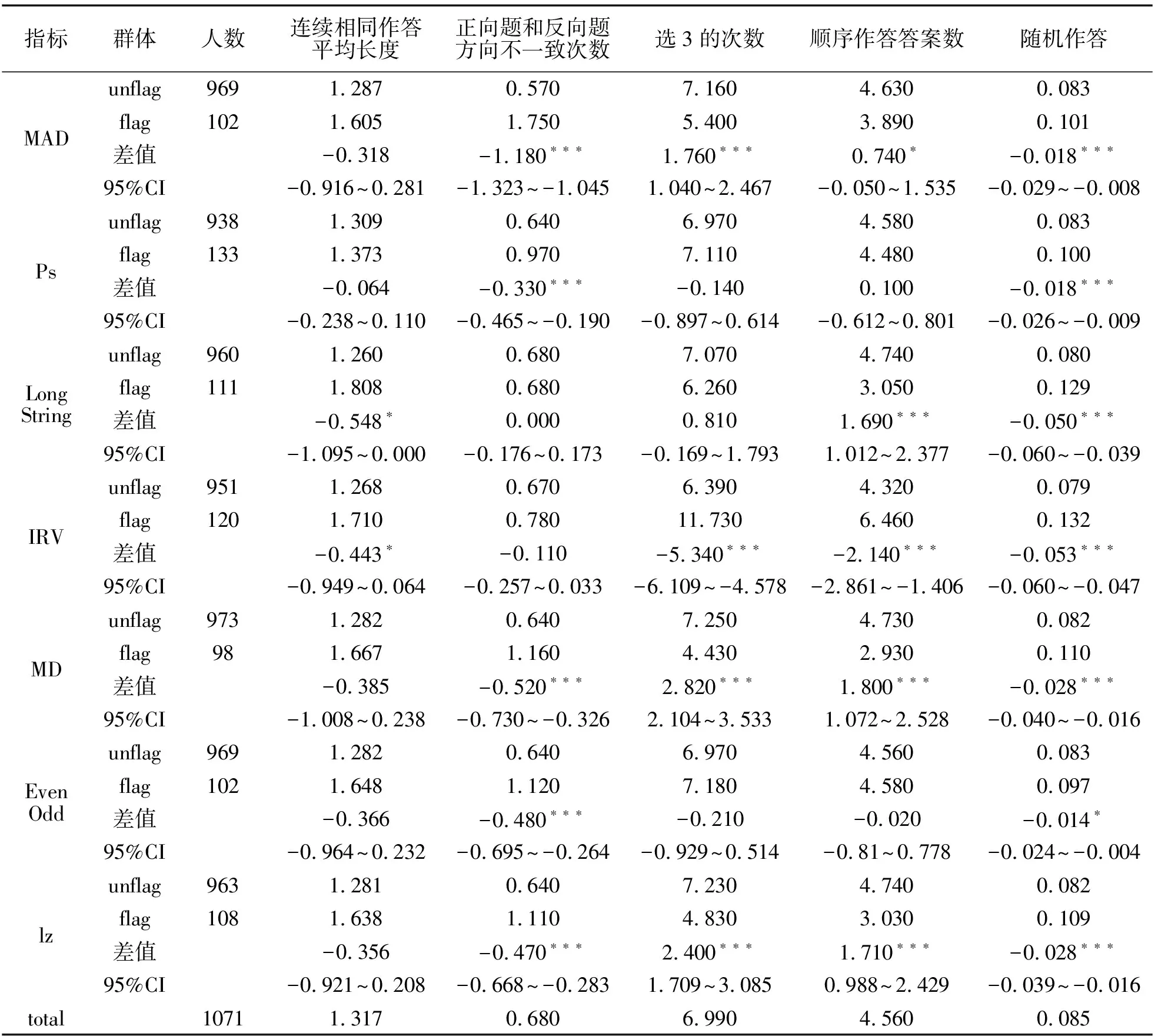
表2 各指标对不同类型IER行为的识别效果

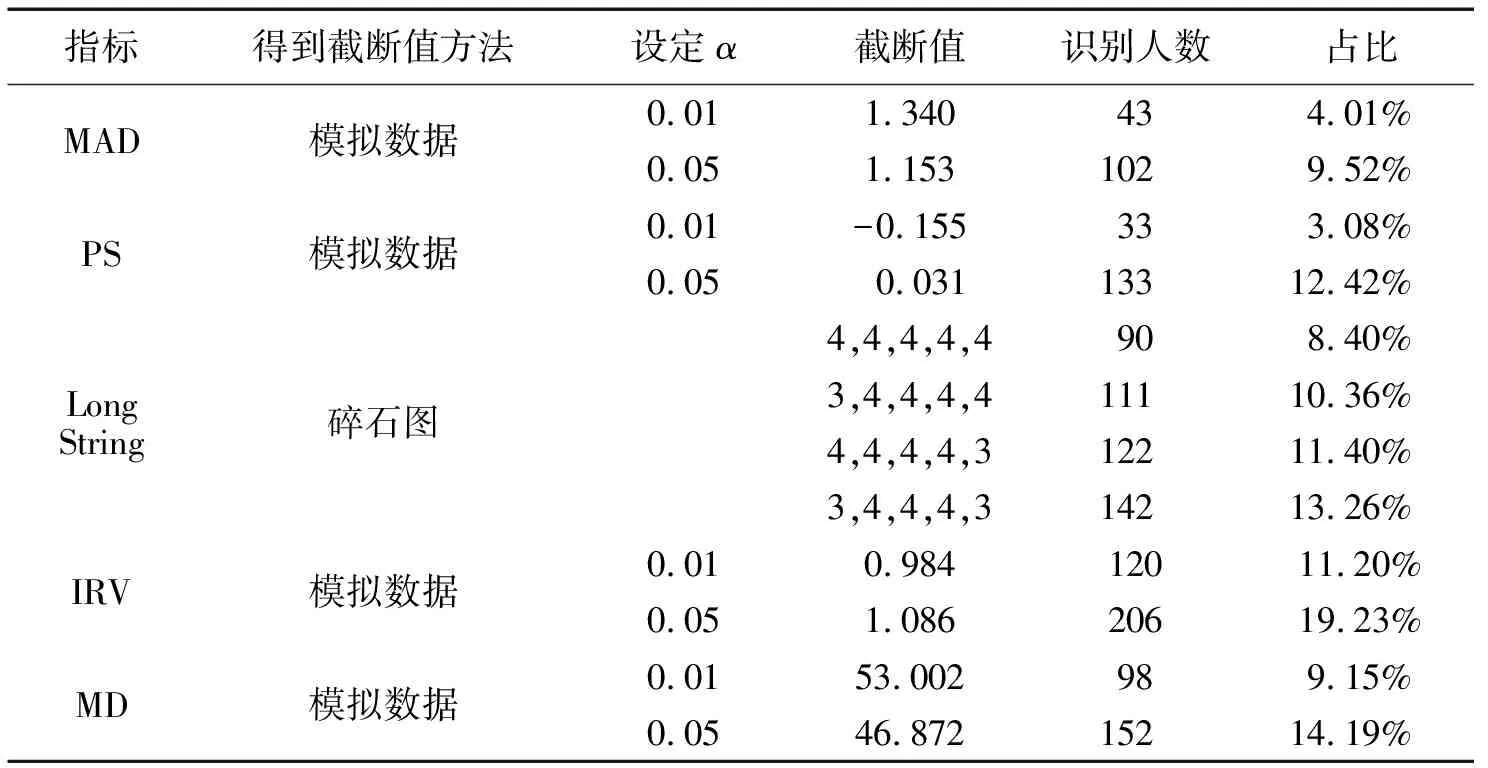
表2 各指标的截断值和识别结果

4 不同方法对不努力作答识别的效果及应用

4.1 研究一 IER指标在不努力作答模式中的适用性

不努力作答的表现形式多样,这里将不努力作答的表现概括为以下五种:

(1)连续相同作答。即连续选择相同答案,比如“3,3,3,3,3,3,3”。

(2)忽略相反题。忽视了当前题目中的相反词,从而出现作答方向错误的情况。

(3)趋中作答。在没有认真阅读题目的情况下,连续选择立场不够明确的中间答案,比如在六点量表中出现大量“3,4,3,3,4,4,4,3,3”模式的作答。

(4)顺序作答。按照顺序选择答案,比如“ABCDABCD……”。

(5)完全随机作答。在不努力作答时,每一个选项都有同等的可能性被不努力作答者选中(Huang et al.,2015),通常毫无规律。

为了研究不同指标对不同IER模式的适用性,针对以上五种不努力作答的模式,就其对应行为的表现特点进行了描述,并在给出了其操作定义见附录表1。

对比每个指标识别出的不努力作答者和努力作答者,在不同模式所对应的操作定义中表现是否有显著差异,从而判断不同指标的模式适用性。采用指标MAD(α=0.05)、PS(α=0.05)、LongString(截断值3,4,4,4,4)、IRV(α=0.01)、MD(α=0.01)、Even Odd(α=0.05)和lz(α=0.01)区分出的不努力作答群体和努力作答群体在五项行为上的表现,两组群体的平均值和差值在附录的表2中呈现,根据结果可知:

(1)对于连续相同作答,连续相同作答平均长度值越大,说明越容易连续选择相同答案。LongString、IRV的识别效果较好,识别的出不努力作答者(IER组)的平均长度值较大,与未识别出的被调查者(安全组)相比差值显著(p=0.025,cohen’sd=0.266;p=0.043,cohen’sd=0.223)。

(2)对于忽略相反题,同一维度下反向题(转换成相同方向后)与正向题分得分方向相反,表明忽略相反题的可能性越大。MAD、PS、MD、Even Odd和lz标注出的IER组忽略相反题的次数更多,与安全组相比差值都显著(p<0.001)。根据差值从大到小依次是MAD、MD、Even Odd、lz和PS(cohen’sd依次为1.589,0.604,0.528,0.547,0.403)。

(3)对于趋中作答,选择“3”的频率越高,说明趋中作答越明显。IRV指标区分出的两组群体趋中作答的频次差异最大,IER组与另一组的差值为5.340(p<0.001,cohen’sd=1.493),说明IRV对趋中作答的识别效果较好。

(4)对于顺序作答,作答数据中顺序作答的数量会较多,说明其按照顺序选择答案的倾向就更明显。IRV识别效果最佳,IER组与另一组相比差值为2.140(p<0.001,cohen’sd=0.558)。

(5)随机作答模式中,以与平均发生率的差值为效标,通常量表中每个选项被选择的频次呈现一定的规律,比如中间选项被选的频次通常较两段的选项高一些,而完全随机作答的数据不会呈现此规律,因此随机选择答案的被调查者的实际选项频率和平均发生率的差值较大。其中差值较大的是IRV、LongString、MD、lz指标(p<0.001,cohen’sd依次为2.393,1.045,0.265,0.262)。

根据表3可知,IRV指标比LongString表现更好,在一定程度上可以替代LongString(Dunn et al.,2018)。在“忽略相反题”中,MD和lz有不错的表现,因此可与IRV组合覆盖全部IER模式,达到取长补短的效果。

表3 不同IER指标的适用情况

对不同方法效果之间的一致性进行分析,大部分指标之间的相关系数虽然显著,但是识别效果的并不完全一致。根据表4可知,MD和lz之间呈现强相关(r=0.528,p<0.001),说明二者甄别结果比较一致,二者与MAD、PS和Even Odd呈现显著正相关;IRV和LongString之间呈现微弱的相关(r=0.161,p<0.001),二者与其他指标的相关关系并不强,甚至IRV与lz和MD呈现微弱的负相关。

表4 同IER指标识别效果的相关系数

4.2 研究二 不努力作答的识别及其对测验信效度的消极影响

Herman和Hilton(2017)认为量表数据质量参差不齐,会对测验工具各项指标的分析产生不可靠的影响。研究二假设删除不努力作答数据之后,会对测验分析提供更准确的工具指标分析结果。在过往的研究中HSQ被证明有较好的信效度,是一个稳定有效的测量工具(詹雨臻,陈学志,卓淑玲,& Martin,2011)。对回收的1071份数据进行分析,可知α=0.862,CFI=0.842,RMSEA=0.060,四个量表的平均相关系数r=0.278,与前人研究结果接近。接下来会以HSQ的数据为例,演示不努力数据清理的步骤,并比较清理前后的工具指标。首先,进行不努力作答数据的清洗。

第一步,通过主动侦查法,清理不努力作答。本量表没有设置测谎题和陷阱题,只有自我汇报准确率,对于准确率不高于50%的数据进行清理;

第二步,通过过程数据清理无效作答。因为缺少作答时间的数据,只能考虑作答缺失,作答缺失在两题及以上的被清理;

第三步,指标识别不努力作答。根据前面研究结果,考虑将IRV指标结合MD或lz指标,对不努力作答进行筛选,截断值与前面一致。

值得注意的是前两个步骤的方法对不努力作答的识别虽准确却不够敏感(Meade &Craig,2012),因此这里将在前两步的基础上结合第三步的指标对不努力作答进行识别,共有六种指标组合,组合1没有加入任何指标,是“题目完成率+自我汇报准确率”,组合2是“题目完成率+自我汇报准确率+IRV”,组合3是“题目完成率+自我汇报准确率+MD”,组合4是“题目完成率+自我汇报准确率+lz”,组合5是“题目完成率+自我汇报准确率+IRV+MD”,组合6是“题目完成率+自我汇报准确率+IRV+lz”。

将原始数据分析得出的工具指标结果作为基线模型,比较六种组合下数据清理后各工具指标的与基线模型的差值。

根据表5可知与基线模型相比,各指标组合清洗后的数据所得内部一致性系数和CFI值基本上都更高,大部分组合的RMSEA均小于基线模型。大部分组合的量表平均相关系数也都高于总体。这说明清理了不努力作答数据之后,其描述测验质量相关的各项指标在大部分情况下基本优于不努力作答的数据,工具的信度和效度的指标计算结果变得更好。

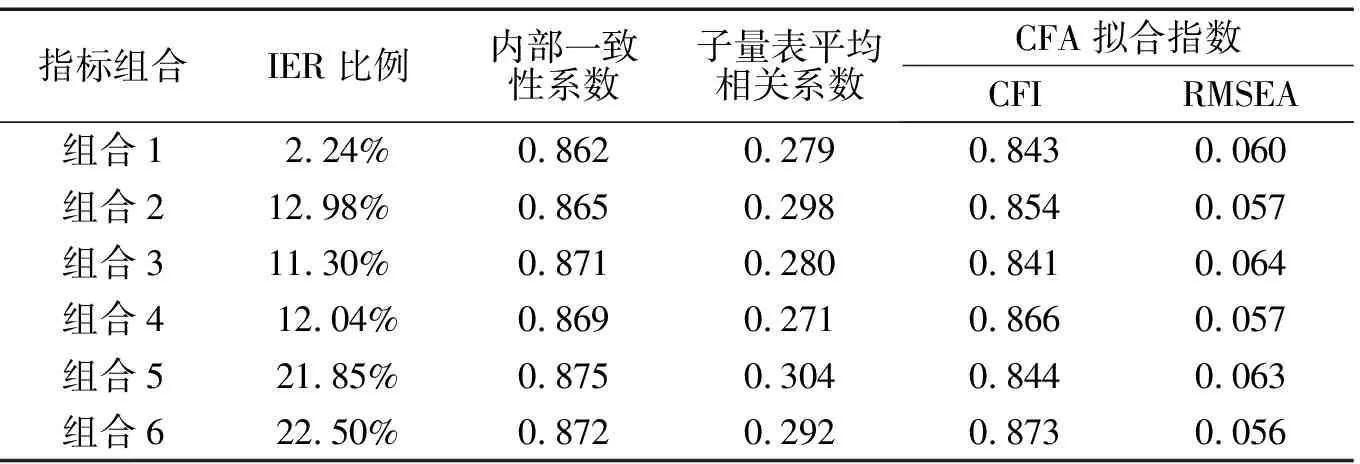
表5 数据清理前后的测验工具各项指标平均数(无IER)

不同组合进行比较,组合2和组合6清理后的数据,计算得出的α系数、拟合指数和平均相关系数皆优于基线模型。说明题目作答率、自我汇报准确率、lz和IRV在对不努力作答数据清理之后,量表的信度、结构效度和同时效度都能得到更好的验证。

5 讨论和不足

除了介绍不努力作答的方法和类型,以及截断值计算,与以往研究不同的是,对不努力作答的行为模式特点也进行了分类和分析,并在研究一中总结了多种识别指标擅长的不努力作答模式。结果表明IRV属于比较综合的指标,仅在忽略相反题的模式上表现不突出,因此可与在该模式表现较好的MAD、MD、lz等指标进行组合筛查。通过各指标识别效果的一致性分析,IRV和MD、lz呈现负相关,这可能是因为MD和lz主要针对无规律的不努力作答形式,而IRV和LongString则主要针对连续相近或相同作答这类有规律的不努力作答模式。因此,各指标对不同的不努力作答行为各有所长,应当将多个指标综合使用取得最佳甄别效果。研究二演示了不努力作答数据清洗的步骤,结果表明多种方法组合清理后的数据质量更好,将题目完成率、自评认真程度、IRV和lz进行组合达到了较好的甄别效果。

不努力作答被认为会对数据分析结果产生消极影响。对比清理前后的作答数据,无不努力作答的数据分析结果显示CFI更高,RMSEA更低,内部一致性系数更好,子量表之间的相关系数也更高。这反映出不努力作答数据对测验工具的信度、结构效度的计算产生消极的影响。努力作答的数据会让分析结果更加稳定,且能更好地拟合量表背后的理论结构,结果也更容易被解释。

对不努力作答甄别方法进行归纳,如表6所示。建议在实际研究中进行不努力数据清洗时,可优先考虑主动侦查法和作答过程指标,因为这些方法是基于被调查者明确的行为,因此更有可靠性,比如作答时间极短的人是无法努力作答的。但这些方法对不努力作答模式不够敏感,检验力有限。比如,由于作答者很容易察觉到预先设置的题目,导致方法失效,因此这类方法识别出的不努力作答者相对其他方法较少(Meade &Criag,2012);同时作答时间只能找出快速作答者,无法甄别出作答速度正常的不努力作答者。倘若缺乏这类信息或想增加检验力,可考虑使用多种IER指标对作答数据进行事后分析和清洗。

表6 不努力作答数据清洗方法总结与建议

根据表6可知,不同方法有各自的优缺点,建议结合多种方法和指标清理不努力作答数据,达到最佳清洗效果。建议采用“MD/lz+ IRV”指标组合进行甄别,在此基础上也可以再考虑MAD、PS、Even Odd等指标作为补充。

本文主要存在以下两方面的不足。首先,缺乏更加有效的效标对各指标的识别效果进行评估。不努力作答的成因复杂,很难用作答表现直接去解释。在研究一中,5种行为仅能说明该被调查者有这样的行为特征,却不能直接说明这样的行为特征完全是由不努力作答引起的,这是存在的局限。其次,根据被调查者自评的准确率可知,不同的被调查者作答认真程度并不相同,目前只是对不努力作答进行了“是”或“否”的区分,却无法评估其不努力作答程度。在后续研究中,对以上两个问题进行深入探讨是有必要的。

6 小结

对不努力作答的常用指标进行梳理,通过一个实际的量表对不努力作答程度以及其消极影响、各指标的具体表现进行了数据分析和探讨,得出以下三个结论:

第一,针对不同的不努力作答行为,不同指标识别效果的并不一致,这反应出不同指标在甄别不同IER行为的效果各有所长。

第二,不努力作答会对数据分析结果产生消极影响,不努力作答的数据会导致信度、效度等指标计算结果变差。

第三,针对心理量表的数据,建议综合采用多种方法和多个甄别指标对不努力作答被试进行识别和清理。