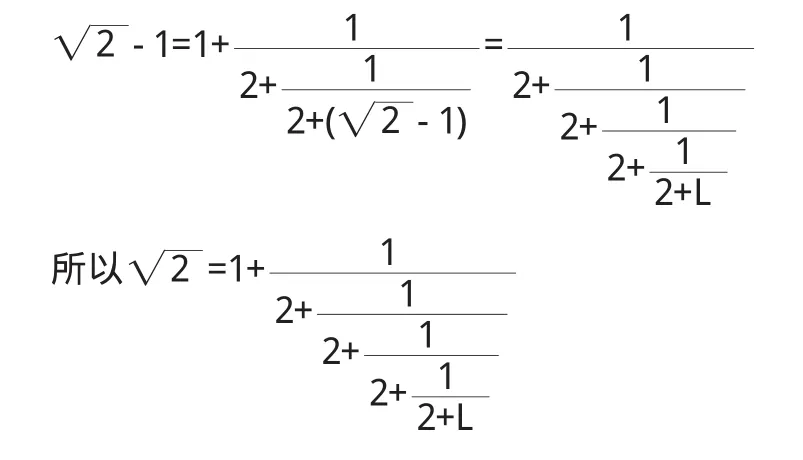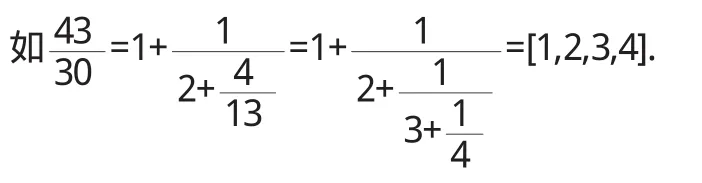论连分数的应用
于海杰
(赤峰学院 初等教育学院,内蒙古 赤峰 024000)
论连分数的应用
于海杰
(赤峰学院 初等教育学院,内蒙古 赤峰 024000)
实数通常用十进制数表示,可写成整数部分与小数部分.实数也可用连分数表示.本文简要介绍连分数的几点应用.
连分数;应用
1 连分数的定义
所谓连分数就是一种特殊类型的繁分数.如
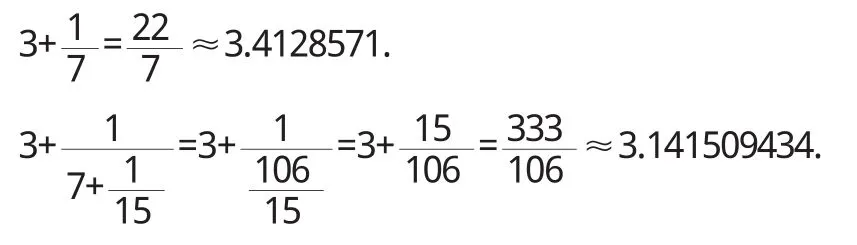
定义 设a0,a1,a2,……是一个无穷实数列,ai>0,i≥1.对于给定的n≥0,我们把表示式
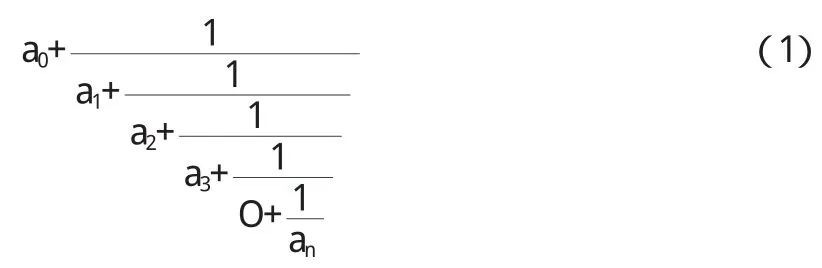
称为有限连分数,通常简写为[a0,a1,a2,……,an].
在(1)式中当n→∞时,我们把相应的表达式

称为无限连分数,通常简写为[a0,a1,a2,……,an,…].
2 连分数与实数的关系
定理(1)有限连分数[a0,a1,a2,……,an]是一个有理数.
(2)任意一个有理数都可以表示为有限连分数.
(3)任意一个无限连分数[a0,a1,a2,……,an,…]是一个无理数.
(4)每一无理数只有唯一一种方法表示成无限简单连分数.
证明略,详见参考文献[1].
3 连分数的截断值
利用分数的连分数表达式的逐次截断值可求出该分数的近似值.
According to the Japanese guidelines on the gastric cancer treatment issued by JGCA (2011)[13], the algorithm of surgical treatment in patients with GC is as follows (Figure 7).
其截断值依次是:
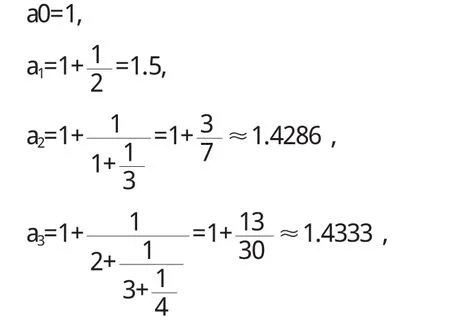
可以发现以下不等式:a0 这说明上述连分数的逐次截断值从左、右两个方向交叉地逐次逼近真值.可以证明,任意一个数的连分数的逐次截断值都有这个渐进逼近性[1],每一个截断值称为渐进分数. 4.1 无理数化为无限连分数 4.2 有理数化为有限连分数 将有理数化为有限连分数,用辗转相除法即可得到. 4.3 连分数在求解一元二次方程方面的应用 例3求x2-3x-1=0的解. 依次得到方程的近似解,而且越往后越精确:3,3.3,L,3.333,3.303L 4.4 利用连分数求最大公约数[3] 例4求61446与18326的最大公约数. 4.5 连分数在历法方面的应用[4] 闰年,是阴历中的一种现象,固定在二月,比平年加一天即29天.我们通常所说的一年365天,其实是个约数,比较准确的应该是365.2422天.那么一年365天就与实际一年少0.2422日,这样四年后就比实际的四年少了近一天,为了弥补这个差值,历法中规定了四年一润,百年少一润. 〔1〕王进明.初等数论[M].北京:人民教育出版社,2007. 〔2〕杨中和.二次无理数的连分数[J].西安文理学院学报(自然科学版),2008(11). 〔3〕袁明豪,等.有限简单连分数的几个应用[J].黄冈师范学院学报,2003(23). 〔4〕徐诚浩.连分数与历法[M].北京:高等教育出版社,2008. O112 A 1673-260X(2014)02-0004-024 简单应用