认知诊断测验的自动组卷方法*
马大付,秦春影,杨建芹,徐新爱,喻晓锋
(1.江西师范大学心理学院,南昌 330022;2.山东省济南市教育教学研究院,济南 250002;3.南昌师范学院数学与统计学院,南昌 330032)
1 前言
测验项目是心理测量学中对被试潜在特质进行间接测量的工具。根据被试在项目上的作答结果,选取合适的模型与分析方法可实现对被试潜在特质的定量化评估(Rupp et al.,2010)。组卷是指从一个已校准的题库中选取一组同时满足统计(如测验长度和精度)与非统计约束(如内容平衡,答案平衡)的项目(Becker et al.,2021;Henson &Douglas,2005)的过程。如不考虑任何约束,从题库中组卷的数量将是巨大的,例如在一个包含20题的题库中选择其中10题进行组卷,共有184756种不同的组卷情况(Finkelman et al.,2009)。而随着题库项目数量的增加和试题管理约束的复杂化,人工组装高质量测验成为一项艰巨的任务(Lin et al.,2019)。自动测验组卷(automated test assembly,ATA;Finkelman et al.,2020)通过将组卷算法与计算机程序相结合,使根据测验需求进行自动组卷成为可能。
认知诊断评估(cognitive diagnosis assessment,CDA;von Davier &Lee,2019)作为新一代的心理测量理论,与项目反应理论(item response theory,IRT)关注被试的连续能力(θ)不同,其更关注对被试离散知识状态(knowledge state,KS)即属性的测量,这使得二者在构建测验的方法上不尽相同。首先,由于θ的连续性,IRT自动测验组卷(IRT-ATA)常采用费舍尔信息量(fisher information,FI)作为测验组卷的方法。测验信息量为测验项目信息量的和(罗照盛,2012),测验信息量越高,测量误差越小,测验信度越高。而KS的离散性不满足FI的对数似然函数具有二阶导数的必要假设(Finkelman et al.,2009),因此基于FI的组卷方法无法直接推广至CD-ATA(Finkelman et al.,2009;Henson &Douglas,2005);其次,二者组卷的复杂程度不同。IRT-ATA与项目参数、被试θ有关,而CD-ATA则受认知诊断模型(cognitive diagnosis model,CDM)、项目q向量、项目参数与KS分布等因素的影响(de la Torre,2011;Song &Wang,2019),并且诊断测验项目q向量之间存在复杂的交互作用(丁树良 等,2010;Lin et al.,2017),这使得即使测验项目的参数相同,q向量的不同组合也会产生不同的诊断结果。最后,即使CD-ATA成功组卷,也不存在精确的数学表达式能够描述测试项目与诊断准确性之间的关系(Lin et al.,2017;Wang et al.,2019),从而无法探知组卷结果的优劣。总之,因认知诊断测量对象的独特性,使得CD-ATA较IRT-ATA而言更加复杂。
为将诊断测验推向实际应用,国内外研究者针对CD-ATA问题提出多种组卷方法。Lin等人(2017)将CD-ATA方法分为:基于指标组卷与基于模拟组卷两类,但却并未对各类组卷方法的发展脉络、组卷思想等进行更深入的探讨。文章通过阅读相关CD-ATA文献,结合国内外最新研究发现CD-ATA方法在整体上有着清晰的发展脉络,不同方法在组卷思想上存在诸多共性之处,且由于技术的发展,当前研究越来越面向实际应用,出现第三类组卷方法。起初,为沿用IRT-ATA使用FI组卷的方式,研究者提出基于信息量指标的组卷方法,并开发多种适用于CDA的信息量指标(汪文义 等,2018;Henson et al.,2008;Henson &Douglas,2005;Song &Wang,2019)。此后,基于作答模拟的方法被提出,该类方法在组卷前模拟一批作答数据,基于该批数据,使用启发式算法(heuristic algorithm)寻求合适的测验项目(Henson &Douglas,2005)。当前,研究者越发关注诊断测验的实际应用,在组卷时考虑更多与实际测验有关的信息,开发基于项目多信息的组卷方法。因此,文章拟对现有的CD-ATA方法进行论述,首先介绍组卷方法的发展脉络及其组卷思想,阐述不同方法之间的联系。其次对比不同类组卷方法之间的组卷思路、方法特征、优缺点,为使用者在方法选用上提供参考;最后,在现有组卷方法的基础上进行研究展望。
2 认知诊断测验自动组卷方法
2.1 基于信息量指标的组卷方法
信息量指标组卷方法试图沿用IRT基于信息量函数的组卷方式,因此定义CDA信息量指标是研究者开发组卷方法时首要解决的问题。根据CDA信息量指标能否直接反映项目的分类准确性,可将其分为间接信息量指标(下称间接指标)与直接信息量指标(下称直接指标)两类。间接指标采用项目对不同KS的区分能力作为项目的信息量,直接指标使用项目的期望分类准确率表示项目的信息量。上述两类指标均采用程序性组卷的方式,组卷时首先选择题库中信息量最高的项目进入测验,而后根据约束条件(如属性最少测量次数)筛选出题库中满足约束的项目,选取剩余题库中最高信息量的项目进入测验,以此类推,直至达到组卷长度。
2.1.1 间接信息量指标
(1)CDI和ADI
相对熵信息量(Kullback-Leibler information,KLI;Chang &Ying,1996)可用于描述两个概率分布的差异而不假设分布连续。项目j上任意两种知识状态αu与αv之间的反应概率分布距离可以描述为:
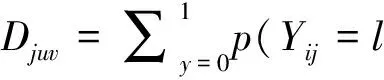
(1)
属性相互独立时,Djuv为一个T*T(T=2K)的D矩阵,K为属性数量。Henson和Douglas(2005)基于D矩阵提出认知诊断指标(cognitive diagnosis index,CDI):
(2)
其中,h(au,av)-1为au与av之间的海明距离倒数。CDIj体现了项目j对所有KS的整体区分能力,项目CDI值越高表示项目的区分能力越强。
Henson等人(2008)认为CDI无法体现项目对单个属性的区分能力,只有当项目考察了某些属性,该项目才在该属性上存在区分能力,且当某些KS对之间的差异较大时,容易对项目的区分能力造成“虚高”的假象。因此可不必考虑差异较大的KS对,仅考虑在单个属性上存在差异的KS对。基于此定义了属性层面的区分度指标(attribute diagnosis index,ADI):
(3)
其中qjk∈{0,1},0表示项目未考察该属性,1表示考察。ADI指标反映了项目在属性层面(attribute-specific)上的区分能力。
测验水平的CDI与ADI可表示为:
(4)
(5)
使用CDI与ADI指标组卷时,通常设置目标函数为Maximize(CDI),Maximize(ADI),即从题库中选择能使CDI与ADI和最大的项目组合,该项目组合有着最大区分能力。Zeng等人(2010)根据可达矩阵能够提高诊断测验准确性的原理,提出在使用CDI编制测验时添加可达矩阵,该方法提高了CDI组卷的诊断准确性。
(2)MCDI和 MADI
Kuo等人(2016)对CDI与ADI展开修正,在原有指标的基础上增加属性层级结构权重与属性最少测量次数权重。校正后的MCDI与MADI(modified CDI;modified ADI)为:
(6)
(7)
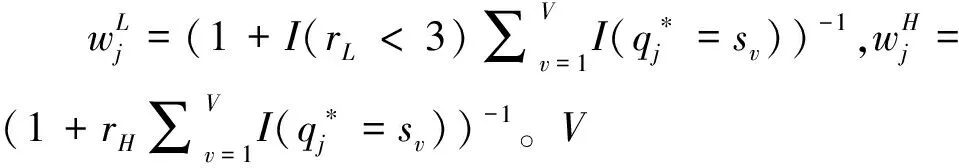
(8)
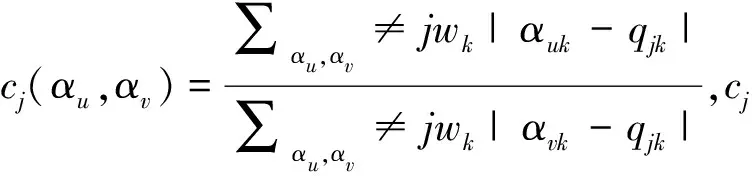
(3)RCDI和 RADI
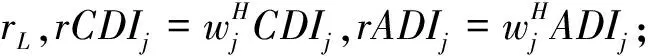
2.1.2 直接信息量指标
基于间接指标的组卷结果仅能表明测验项目具有较高的区分能力和可能具有较高的诊断准确率,却无法直接判断组卷结果的属性或模式判准情况。汪文义等人(2018)以及Song和Wang(2019)提出一种可在无作答数据的情况下对项目各属性分类准确性进行预测的直接指标:期望属性分类准确率指标(expected attribute match rate,EAMR):
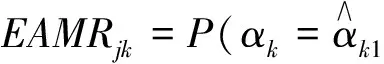
(9)
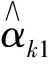
(10)
EAMRjk表示掌握属性k的被试在项目上正确作答并最终分类正确与未掌握属性k的被试在项目上错误作答并最终分类正确的概率之和。当属性k未被项目考察时,项目对该属性的期望正确分类率为0.5。项目j的EAMRj为各属性的EAMRjk之和。
同样的,测验水平的EAMR为:
(11)
2.1.3 信息量指标优化算法组卷
除上述两类信息量指标方法外,Finkelman等人(2010)认为,在定义CDA项目信息量指标后,CD-ATA应回归IRT-ATA使用优化算法的整体性组卷方式,优化算法的组卷结果可被证明是满足条件下的最优信息量指标项目组合。
(1)0-1整数线性规划组卷
0-1整数线性规划法(binary integer liner programming,BILP)常用于在给定目标函数与多个约束条件的情况下,优化目标函数值。Finkelman等人(2010)将BILP用于CD-ATA。以ADI指标为例(也可使用其他指标),设定目标函数:
(12)
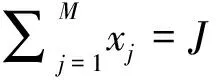
(2)混合整数线性规划组卷
混合整数线性规划方法(Mix Integer Linear Programming,MILP)的目标函数中既包括整数型决定变量,也包括连续型决定变量。Wang等人(2021)将该方法与项目D矩阵相结合,将其用于CD-ATA。该方法首先去除项目D矩阵中对角线为0的元素,后将D矩阵转换为长度为T-1的矩阵,再将其转换为列向量后按行拼接。经上述三步处理,将D矩阵转换为行为T(T-1),列为1的项目列矩阵。将题库中所有项目列向量按列合并为一个大小为行为T(T-1),列为M的题库矩阵:V矩阵。设置目标函数为:
min(f1x+f2y),
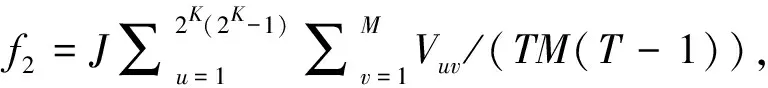
当不考虑f2y部分时,MILP方法与BILP方法类似,两者均是基于项目的KLI,不同的是MILP基于项目的D矩阵,而BILP则是基于项目的CDI值。当考虑f2y部分时,相较于BILP方法,MILP方法保证了对每对KS进行足够的区分度测量,即区分度平衡。
2.1.4 基于信息量指标的组卷方法评价
基于信息量指标的组卷方法的结果与所定义的CDA信息量指标密切相关,由于属性的离散性,现有研究在定义CDA信息量指标时始终沿用一种如何将不同KS充分区分的思路。在得到信息量指标后,根据测验信息量最大化的组卷思想进行确定性组卷,即在确定题库项目、组卷指标、测验要求后,任一基于信息量指标的组卷方法从题库中所选择的项目是确定的。因仅进行一次组卷,而未与其他可能的组卷结果进行比较,这导致其组卷结果未必是全局最优。
2.2 基于作答模拟的组卷方法
该类方法通过事先模拟被试在项目上的作答数据,通过设立目标函数,将CD-ATA问题转换为在已有数据上寻求一组最符合目标函数的项目组合。由于能为诊断目的设立不同的目标函数,因此相较指标组卷方法,作答模拟组卷方法灵活度更高(Finkelman et al.,2009)。
2.2.1 遗传算法组卷
遗传算法(generic algorithm,GA)模拟自然界优胜劣汰的进化过程:具有更强适应能力的个体将在个体竞争中存活,并产生具有更强生存能力的后代。Finkelman等人(2009)将该方法用于CD-ATA。GA将题库中测验项目组合被视为单个个体,通过比较不同个体符合目标函数的程度,选择当前数据下接近最优的测验组合。GA的具体组卷过程包括以下几步:①产生一批包含S组初始项目的测验即父代,每个测验中包含数量为J的项目组合,初始项目组合可随机产生也可通过使用CDI的组卷方式产生;②使用“变异”策略,随机改变每个初始解中的一个项目,产生S*J个子代;③评估包含父代在内的S*(J+1)组解符合目标函数的程度;④根据③步的评估结果,选择最符合目标函数的前S组测验项目组合进入下一轮迭代;⑤重复步骤②-④,直至达到最大迭代次数;⑥选择最后一次迭代中最优项目组合做为最优测验。
为使组卷结果更加符合实际,Finkelman等人(2009)提出三种目标函数:
(13)
(14)
(15)
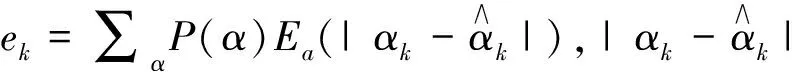
2.2.2 蚁群算法组卷
蚁群算法(ant colony optimization,ACO)与GA类似,均属于求取目标函数的启发式算法。Lin等人(2017)将ACO用于CD-ATA,提出基于蚁群算法的测验构建方法(test construction method based on ant colony optimization,ACO-TC),该方法将CD-ATA视为一种路径优化问题,题库中每一种测验项目的组合均被认为是一条路径,通过建立目标函数,在所有路径中寻求接近最优解的路径。
ACO-TC过程大体上可分为三步:局部组卷、局部信息量更新与全局信息素更新。局部组卷时,单个蚂蚁(a=1,2,…,A)从剩余题库中选择满足条件约束的项目j的后验概率可为:
(16)
其中T为剩余题库中满足约束的项目集合,τj为项目的信息素浓度(初始组卷时设置τ0=1),ηa与γa分别为项目信息量指标与项目满足测验约束程度的权重,为提高组卷过程中的适应性,可设置ηa为多种项目信息量指标的组合。当蚂蚁a完成组卷后对其所选中的项目进行局部信息量更新:
τj=(1-ρ)τj+ρτ0,
(17)
公式(17)中的ρ∈(0,1)表示信息素蒸发速率。当所有蚂蚁均完成组卷后,可设置公式(13)、公式(14)、公式(15)为目标函数,评估所有蚂蚁的组卷结果,最优项目组的目标函数可记为fbest,最差组记为fworst。后对fbest中的项目进行全局信息量更新:
τj=(1-ρ)τj+ρΔτ,
(18)
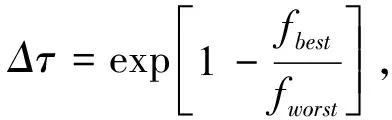
2.2.3 基于作答模拟的组卷方法评价
作答模拟组卷方法依靠自身不断的循环迭代,每一次的组卷结果都建立在上一次组卷结果的基础之上,寻求更优于上一次组卷结果的题目组合,当组卷结果不再变化时,则表示寻得当前组卷方法下的最优题目组合。这种循环迭代的组卷方式,提高了找到全局最优解的可能性。但由于其需要大量的迭代计算,需要耗费的组卷时间也相对更长。
2.3 基于项目多信息的组卷方法
在实际测验中,测验的项目构成、测验形式以及测验的时限要求等都是测验开发者应当考虑的问题。为使组卷结果与实际测验要求更加一致,研究者进一步考虑更多可利用的项目信息,开发得到基于项目多信息的组卷方法。
2.3.1 基于多选项项目的组卷方法
现有研究对诊断数据的处理往往采用二分法(正确作答与错误作答两类),多项选择认知诊断模型(multiple choice CDM,MC-CDM)认为错误选项同样包含着属性的分类信息,这些信息同样可被可用于KS判别(Henson et al.,2018)。Henson等人(2018)将DINA模型下的区分度指标:1-sj-gj,用于MC-CDM,提出一种广义的区分度指标(discrimination index,DI):
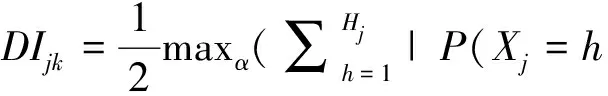
(19)
Hj表示项目j的选项数量,P(Xj=h│α)表示α的被试选择选项h的概率,Pjh(Xj=h|α-k)表示与α仅在第k个属性上存在差异的KS选择选项h的概率。DIjk定义了单个项目对属性k的区分能力。在使用DI组卷时,采用与CDI相同的指标线性求和的方式,测验水平的DI为:
(20)
2.3.2 基于反应时的组卷方法
Finkelman等人(2020)认为,尽管当前CD-ATA已能够获得丰富的信息,但还要保证被试所花的时间是可接受的,许多测验也含有一定的时限要求,因此其将反应时信息融入CD-ATA,作为测验组卷的约束条件,提出反应时组卷(response time assembly,RTA)。基于van der Linden(2006)提出的项目反应时模型:
(21)
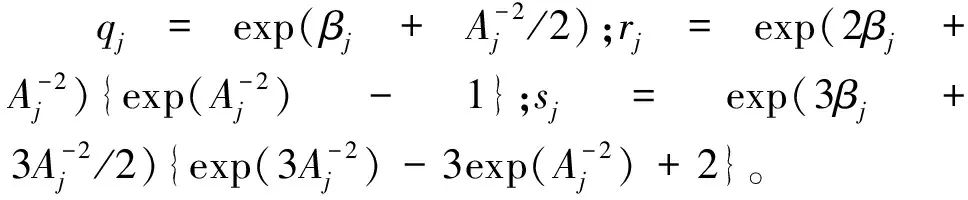
(22)
(23)
(24)
其中ζq,ζr与ζs分别表示q,r与s的目标条件,δs,δs与δs分别表示q,r与s的可容忍残差。在CD-ATA组卷时,RTA方法与BP相同,组卷时将反应时信息作为一种额外的约束条件,使用LP求解器进行求解。
2.3.3 基于项目多信息的组卷方法评价
基于项目多信息的组卷方法在测验形式、测验要求等方面上更加贴合于实际情况,在组卷时考虑更多对测验结果可能产生影响的因素,并将其纳入组卷过程。但其对项目本身的要求更高,如多选项项目组卷方法需知道选择错误选项的概率,反应时组卷方法需知道作答项目的时间分布情况。
3 组卷方法比较与选用
3.1 组卷方法比较
文章已对现有的十多种CD-ATA方法进行介绍。接下来进一步对不同组卷方法进行比较,为实际使用者以及后续研究者在选用方法与开发新方法提供思路。表1详细呈现了不同组卷方法的分类情况、方法特征及优缺点。

表1 不同CD-ATA方法对比
从方法的大类上可以看出:①信息量指标组卷方法沿用IRT-ATA使用FI线性和的组卷思想,根据属性离散的特点,在CDA中寻找Fisher信息量的替代品。在组卷时通常设置满足约束条件的最大测验信息量项目组合,为确定性组卷方法。然而,该类组卷方法忽视了CD-ATA与IRT-ATA的不同,未考虑项目q向量之间复杂的交互作用,缺乏灵活性。②与信息量指标组卷不同的是,作答模拟组卷方法选择项目时是非确定性的,题库中的每个项目都有被选入测验的概率,为概率性组卷方法。通过不断地迭代更新,每次迭代后的结果均优于上一次迭代,最终得到最优项目组合。相较于信息量指标组卷方法,模拟作答组卷在组卷时尝试的项目组合类型更多(信息量指标组卷仅尝试一种项目组合)。但由于其算法复杂,计算量大,导致其组卷效率较低。③项目多信息组卷对项目信息了解程度要求高,且在组卷时部分依赖指标组卷的方法,因此也部分具有指标组卷存在的缺点。
3.2 组卷方法选用
通过对不同方法的比较,文章从组卷精度与组卷效率两种角度,为实际使用者在选用组卷方法上提供建议。
(1)组卷精度,诊断测验的首要目的是为获得较高的诊断精度(Rupp et al.,2010),尽管不同组卷方法存在一定的精度差异,但相较于随机组卷,本文所提及的组卷方法在属性数量较少的情况下均能够获得较高的判准精度。但属性数量较多时,指标组卷方法的判准率将迅速下降(Henson &Douglas,2005;唐小娟 等,2013),此时应当选用模拟组卷方法。另外,当组卷的目的是为了获得特定属性精度的测验时(Finkelman et al.,2009;Lin et al.,2017),指标组卷方法将无法适用,此时仅能通过模拟组卷。
(2)组卷效率,除组卷精度外,组卷效率也是施测人员需要考虑的问题(Finkelman et al.,2009;Lin et al.,2017)。模拟组卷因其在组卷时需不断地迭代更新项目组合,计算要求高,组卷时间长,组卷效率低。其他方法仅需在前期计算项目信息量指标时耗费一定的时间(郭磊 等,2016),实际组卷的时间较短,而且由于指标组卷均属于确定性算法,因此仅需计算一次项目信息量,即可多次运用。因此,如希望在短时间内得到组卷结果,可选择基于指标组卷的方式。
4 研究展望
尽管现有的CD-ATA方法已达十余种,但面对实际测验的多样性,有关组卷方法的研究与应用均有待进一步拓展,文章在已有方法基础上从理论性研究和实际应用角度出发提出几点展望。
融合测验设计,基于信息量指标的组卷方法仅关注于单个项目的q向量与项目参数,未考虑诊断测验的整体性,忽略测验Q向量在诊断测验中起到的重要作用。目前已有部分关于测验构建策略的研究(唐小娟 等,2022),而仅有少数组卷研究探讨过将信息量指标组卷方法与测验构建策略进行融合,融合测验构建策略后的结果也表明,信息量指标组卷方法的组卷精度可获得大幅增长(Kuo et al.,2016;Su &Chu,2021;Zeng et al.,2010)。未来可进一步探讨将更多诊断测验设计与信息量指标组卷方法相互融合,在保证信息量指标组卷效率的基础上,进一步提高其组卷精度。
非参数组卷,当前CD-ATA方法均是在假定项目参数已知的情况下进行,而实际情况中,项目的实际参数是难以获得的。尤其是对于一些具有较复杂的诊断模型而言,准确的项目参数估计依赖于大量被试的作答反应。而当项目参数稳健性难以保证的情况下(Veldkamp et al.,2013),使用非参数组卷方法则势在必行,未来可开发更多非参数组卷方法。
平行测验组卷,平行测验(parallel test)是一种常用的实际测验形式,而文章所介绍组卷方法均只针对于构建单份测验。在查阅文献后,发现当前有关认知诊断平行试卷的构建方法仅有少数研究者(Li et al.,2021;Lin et al.,2019)有过相关探讨。未来也可开发同时能构建多份平行测验的CD-ATA方法。
开发组卷软件,尽管当前已开发了多种CD-ATA方法,但这些方法并不适用于没有编程基础的使用者,这也在一定程度上阻碍了组卷方法的实际应用。目前,有关研究者已将IRT-ATA组卷方法开发为相应的软件与开源R包(Becker et al.,2021;Shao et al.,2020),使用者仅需少量操作便可进行组卷,极大的简化了组卷过程,而CD-ATA中目前仅可通过使用R中的CDM包计算CDI与DI指标(George et al.,2016;Shi et al.,2021),尚未见完整的组卷R包或专业组卷软件,未来可开发相应诊断组卷软件。
开展实证研究,当前CD-ATA的实证研究相对较少。这一方面是由于国内外诊断测验的研究尚处于起步阶段,缺少系统性的测验开发、题库建设的过程,这在一定程度上阻碍了CD-ATA的实际应用。考虑到CDA在教学评估过程中的优良特性、未来可开发系统性的诊断测验题库,开展CD-ATA的实证研究。

