温度对不同预加张力作用下的电容式压力变送器测量精度影响

李富强,陶友瑞，2,郑楠纤,段书用，2

(1.河北工业大学机械工程学院，天津 300401;2.河北工业大学，电气设备可靠性与智能化国家重点实验室，天津 300401)

0 引言

工业过程检测与控制中，压力仪表占现场仪表的三分之一左右[1]。电容式压力变送器作为压力测量与流量测量仪表的核心部件，其工作原理为当外界压力作用于隔离膜片，隔离膜片发生变形引起δ室内的传递介质流动，导致施加预加张力的中心测量膜片在压差作用下产生变形位移，引起固定电极和测量膜片之间距离的变化，从而使二者电容量发生改变，电路控制部分将电容量的变化转换成电压的变化，生成输出信号，利用电学方法间接测量得到压力差值或压力值。同时电容式压力变送器是直接与被测介质接触的现场仪表，常在高温、腐蚀、振动、冲击等环境中工作。由于工艺流程的大型化、复杂化及智能化的未来发展要求，对检测仪表的精度、稳定性、可靠性提出了更高的要求[2]。据相关研究表明，我国自行研发的中高档仪器仪表的性能参数已与国外产品十分接近，但受制于工业性能测试评估体系的缺失，导致影响仪表可靠性的指标尚不明确，无法评估仪表的可靠度，有可能出现故障漏报和误报现象[1]，因此，在综合电容式压力变送器仪表的三大误差影响精度因素的基础上[2]，本文分析温度和测量膜片预加张力对于电容式压力变送器测量精度的影响。对于电容式压力变送器测量精度的温度影响，已经有一系列的相关研究。徐国传[3]分析了电容式压力变送器的综合误差主要由仪表本身的测量精度A，环境温度变化带来的误差T以及静压变化带来的误差S3部分构成。由此可见，环境温度变化对于变送器的测量精度的影响不容忽视。使用电容式差压变送器测量时，需要对温度误差进行补偿或校正，减少其对测量精度的影响。赵东峰[4]说明了电容式压力变送器δ室内的传递介质会随温度变化从而对测量精度产生影响，这是温度误差产生的一个主要因素。杜建生[5]分析了电容式压力变送器实际使用情况下的各类故障，存在由于测量介质温度过高导致膜盒组件靠近测量端侧的δ室内的传递介质膨胀导致仪器仪表损坏的实例。在实际情况中，存在由温度引起的电容式压力变送器的零点漂移误差，并且漂移误差会随温度变化而变化。郑萍等[6]说明了压力变送器如何选择温度电阻，通过温度补偿电路进行温度误差的补偿。由于是通过3个温度点来进行温度电阻的选择，温度电阻的选择方法简单，调节范围有限，很容易因为温度电阻选择不恰当导致压力测量不准确。蒲明辉等[7]针对差动平行极板初始极距不同的问题进行误差分析，得到一种误差校正方法。揣荣岩[8]等分析了电容式双动极板的结构特性，发现其线性范围提高，降低了非线性范围。尽管目前针对电容式压力变送器的温度影响因素的研究众多，但是这些分析与研究结果大多是聚焦于单纯的温度变化及其补偿研究，对于电容式压力变送器内部结构部件耦合温度影响分析涉及不多。事实上，通过电容式压力变送器的工作原理可知，其内部构件测量膜片的预加张力对于温度误差也有十分重要的影响。王思仁[9]通过对电容式压力变送器工作原理的分析得到电容式压力变送器是由测量环节和转换环节构成开环结构设计，虽然结构简单，但是由于开环，各个环节的误差会按照1∶1的关系传递到后级。孟岳[10]分析了电容薄膜真空计的感压膜片的预加张力与位移的关系，其在不同预加张力作用下受到不同压力载荷产生的位移变化是不同的。因此测量膜片结构参数的改变叠加上温度误差，会对整机性能产生不可忽视的影响。

本文在已有研究的基础上，对某电容式压力变送器通过DIC(digital image correlation，数字散斑相关法)实验反求其内部测量膜片的预加张力，然后采用液体热膨胀的流固耦合等效分析方法[11]对不同预加张力条件下的测量膜片的温度-位移进行数值模拟。在此基础上分析测量膜片位移变化和相对基准位移的位移偏移量ε随温度和预加张力的变化规律。

1 计算方法与模型

1.1 计算方法

本文主要研究电容式压力变送器膜盒的测量膜片在不同预加张力条件下，由于膜盒两侧的δ室温度分布不均匀，导致温度较高的δ室内的传递介质产生温度膨胀，分析20～70 ℃的温度变化对其测量精度的影响。利用等效表面载荷的方法并结合液体温度、压强和体积之间的关系，设定在电容式压力变送器膜盒中，温度升高导致的传递介质膨胀对于膜盒的作用是均匀分布的，传递介质为不可压缩流体，不需要考虑传递介质的黏度随温度变化情况以及流动阻力。在隔离膜片和中心测量膜片的弹性变形内，隔离膜片和中心测量膜片的受力决定了其变形的大小，将液体模型的温度膨胀变化等效为压力变化，省去液体分析模型。通过逐渐加大压力来模拟温度升高的效果，控制方程[11]的计算表达式为

(1)

式中：K为液体的体积模量；ρ0为初始温度下液体的密度；p为在容器内壁施加垂直于内壁表面且处处相等的压力；V0与V1分别为变形前和变形后的体积；ρT为各参数代入PVT公式后求得的等效液体的密度。通过对比液体在不同温度下的密度分布[12]，可得到此时等效液体的温度T。

本文中甲基硅油体积模量满足式(2)：

K=ρc2

(2)

式中：ρ为甲基硅油密度；c为甲基硅油体积声速。

1.2 膜盒建模

以某款实际型号的电容式压力变送器为例，通过对其进行结构拆分并结合工作原理分析，其主要由结构部件和电路部件构成。膜盒是其核心结构部件。图1为膜盒工作原理示意图，图2为膜盒结构示意图。膜盒由两侧相同的波纹隔离膜片，中间为施加预加张力的中心测量膜片和2个相同的半杯体构成。其中半杯体由陶瓷体、玻璃体和半杯体壳体组成，三者在具体的膜盒结构中被加工组成一个结构整体，因此在膜盒仿真分析中视为一个整体参与仿真分析。膜盒内部的传递介质为甲基硅油液体，储存在由隔离膜片，半杯体和中心测量膜片三者共同构成的密封的δ室内，δ室容积为2 mL，两侧各一。

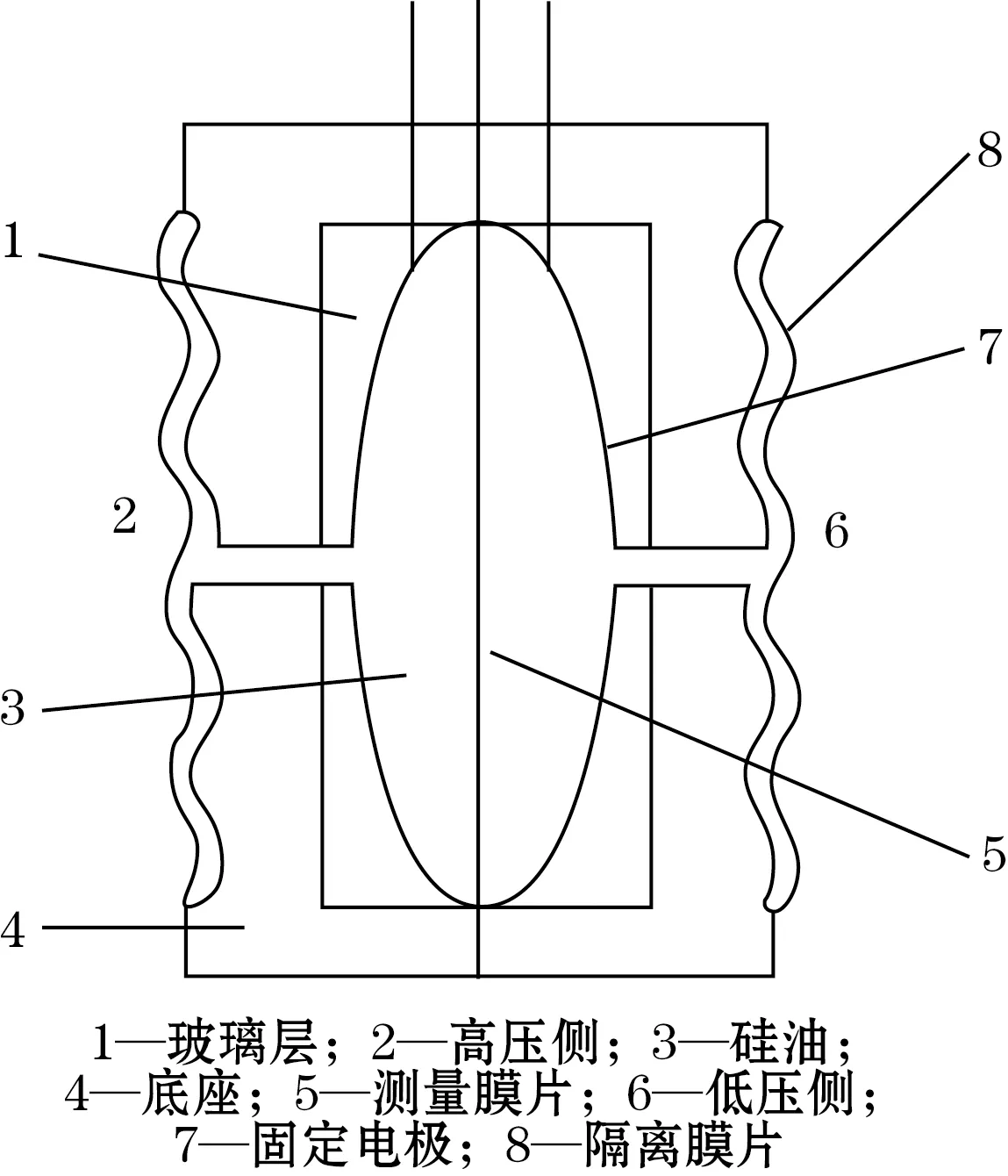
图1 电容式压力变送器膜盒原理示意图

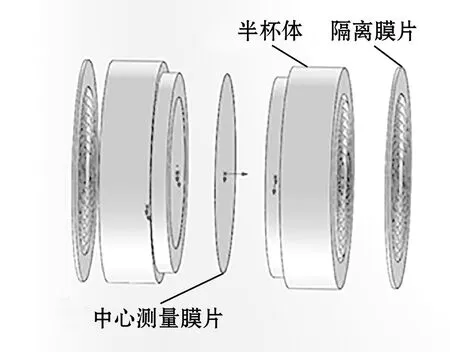
图2 电容式压力变送器膜盒结构示意图

通过对膜盒的结构拆解及工作原理的分析，结合主要研究问题及分析方法，确定主要分析部件为波纹隔离膜片，中心测量膜片以及传递介质。据此对结构进行简化。由于在20～70 ℃条件下，液体的温度变化效果远大于金属部件的温度变化效果，因此将半杯体部分认为是构成液体存储结构的一部分，不参与仿真分析。同时将膜盒结构理想化，不考虑其中金属零部件的结构中材料的缺陷和加工过程等产生的残余应力。

1.3 仿真分析建模

由于利用流固耦合的等效方法分析，流体模型可以进行等效处理，因此对固体结构部分进行建模。表1为膜片材料的力学性能参数表，表2为波纹隔离膜片的型面参数表。波纹隔离膜片的直径为30 mm，厚度为0.05 mm，波纹采用正弦波形，膜片材料为316L钢，该材料具有良好的耐腐蚀性和强度，能有效减小外部测量介质对隔离膜片的危害，延长变送器的使用时间。

表1 膜片材料力学性能参数表

表2 波纹隔离膜片型面参数表

图3为波纹隔离膜片网格划分模型。因为波纹隔离膜片的径向形状是具有高度空间对称的圆形，其径向和轴向的宽厚比很大，采用壳单元来进行有限元分析。将模型划分为5个部分方便网格划分，最大网格大小控制在0.5mm，最后经过统计得到节点数为18 145个、单元数为18 418个的波纹隔离膜片网格划分模型。

图3 波纹隔离膜片网格划分模型

测量膜片的直径为30mm，厚度为0.1mm。膜片材料为结构钢。因为中心测量膜片在膜盒中受到传递介质的保护，不直接接触外界的测量介质，并且结构钢属于常用材料，经济适用性好。结构钢的力学性能参数如表1所示。

图4为中心测量膜片网格划分图。由于中心测量膜片的径向形状是具有高度空间对称的圆形，其径向和轴向的宽厚比很大，利用同样的方法进行处理。采用自动网格划分技术，最大网格大小控制在0.5mm，最后经过统计得到节点数为3 476、单元数为3 401的中心测量膜片网格划分模型。

图4 中心测量膜片网格划分模型

1.4 边界条件设定

由于实际情况下，电容式压力变送器的中心测量膜片具有预加张力。因此参考孟岳[10]分析电容薄膜真空计和任凤琴[13]的热胀式膜片张紧装置原理，在仿真中通过对中心测量膜片施加一个径向位移来等效代替预加张力，利用传递介质热膨胀应力分析的等效方法将温度变化导致的膜盒一侧的δ室内的液体膨胀效果等效为膨胀压力，将膨胀压力作为均布载荷施加到中心测量膜片一侧，另一侧相对取零。同时为了提高计算的精度，减小非线性误差，打开静力学分析模块的大变形功能。

2 预加张力反求

2.1 DIC实验

DIC(digital image correlation)是一种非接触式的用于全场形状、变形、运动测量的方法，它直接处理的对象是具有一定灰度分布的数字图像(散斑图)，通过对比材料或者结构表面在变形前后的散斑图，运用相关算法得到全场位移和应变。该方法对实验环境要求极为宽松，并且具有全场测量、抗干扰能力强、测量精度高等优点。

DIC实验方法：为了模拟膜盒受到外界测量介质的液体压力，采用弹簧、硅橡胶和旋转抓马构成压力施加设备，通过压力计算公式结合弹簧刚度系数等参数计算位移，可以实现旋转抓马的不同位移来模拟液体不同压力的施加情况。对膜盒一侧(设定为A侧)波纹隔离膜片施加模拟压力0.2 MPa，采用DIC设备，分析另一侧(设定为B侧)波纹隔离膜片的变形位移情况。具体实验流程和实验现场如图5、图6、图7所示。

图5 实验流程

图6 实验现场1

图7 实验现场2

2.2 DIC实验结果分析

图8为通过DIC实验得到的B侧波纹隔离膜片的位移变形数据图。图9为通过仿真分析得到的中心测量膜片的变形结果。分析数据得到如下结果：B侧波纹隔离膜片最大位移处为中心处，波纹膜片最大位移约为0.18 mm。

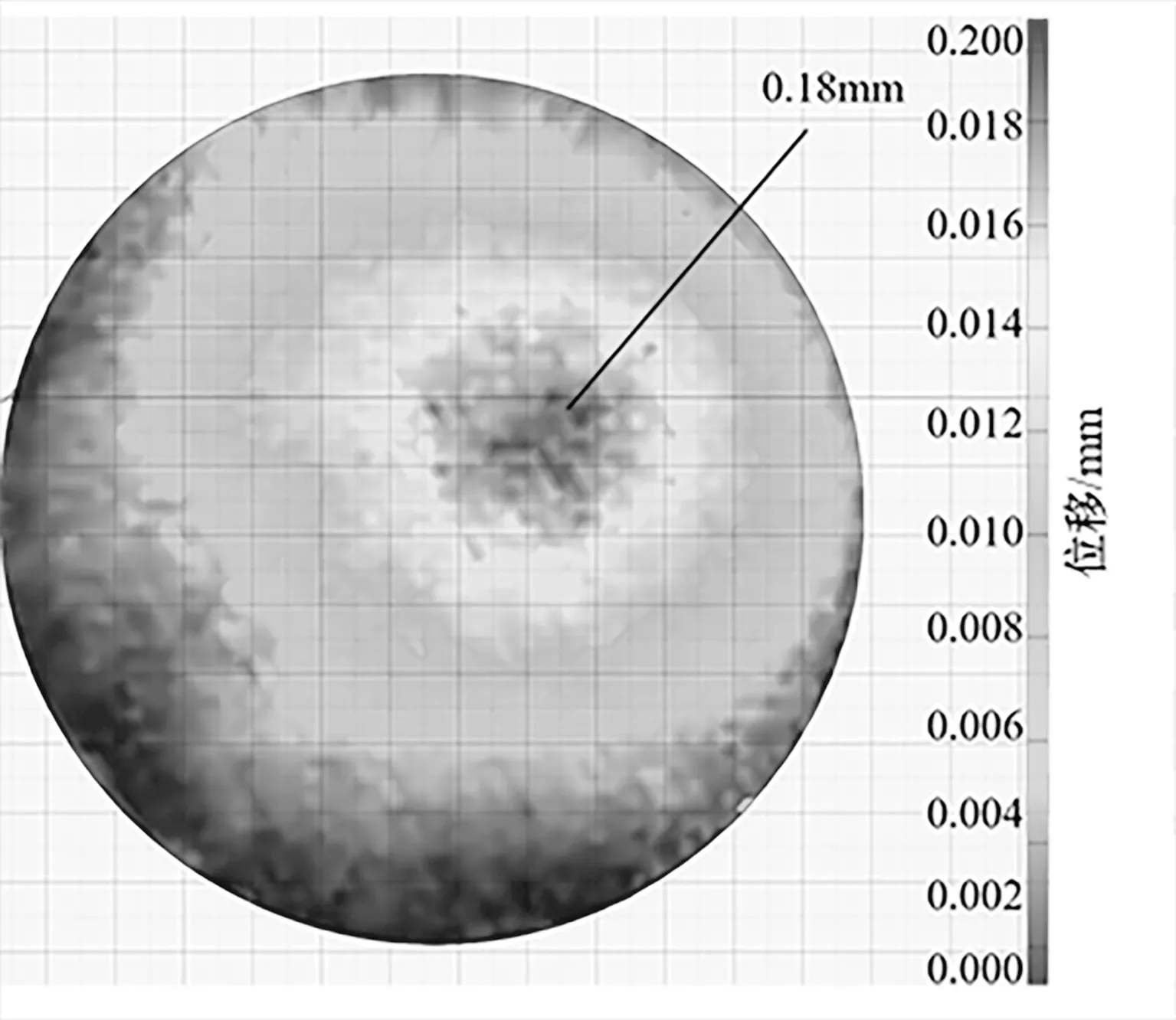
图8 波纹隔离膜片位移变形数据

图9 中心测量膜片预加张力44 MPa时的变形

当A侧隔离膜片的变形导致δ室内的传递介质产生流动，传递介质传递压力使中心测量膜片产生变形，按照同样的作用方式分析可得，压力最终传导到另一侧B侧波纹膜片，使其发生变形。利用传递介质液体的不可压缩性条件，于是B侧波纹隔离膜片变形前后容积变化V1等于中心测量膜片变形前后容积变化V2。采用陈新华[14]提出的容积公式简化计算波纹隔离膜片在小变形条件下的容积变化：

(3)

式中：S为波纹膜片最大变形位移；R为波纹膜片最大变形半径；r为波纹隔离膜片中心硬芯处半径。

利用容积公式简化计算平膜片在小变形条件下的容积变化：

(4)

式中：H为中心测量膜片最大变形位移；R为中心测量膜片最大变形半径。

通过小变形位移计算公式可以得到V1和V2，结合流体不可压缩条件，利用V1=V2，经过计算得施加某预加张力的中心测量膜片在0.2 MPa压力下的位移应该在0.22 mm左右。表3为中心测量膜片在不同预加张力条件下的仿真分析结果，最终得到了在施加给中心测量膜片预加张力44 MPa时，中心最大位移为0.19 mm，符合相关实验结果和分析数据，如图9所示。由此建立了完善的中心测量膜片的参数信息。

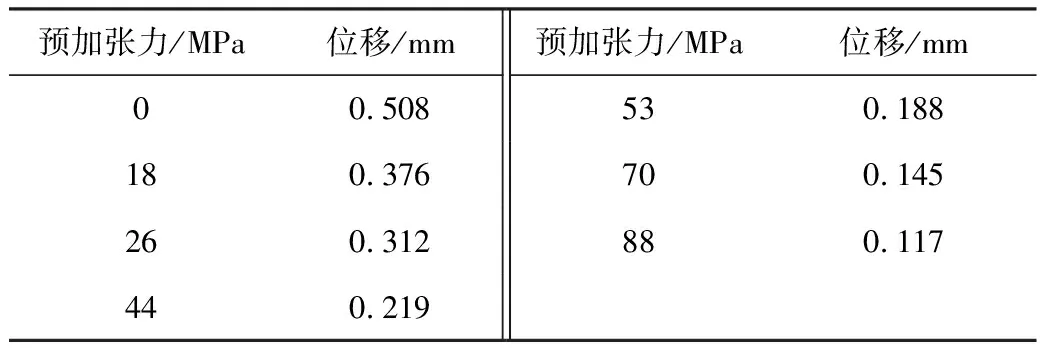
表3 中心测量膜片的不同预加张力仿真分析

3 结果分析

3.1 预加张力为44 MPa时，不同温度下的位移变形分析

利用DIC实验得到中心测量膜片的实际预加张力为44 MPa，结合计算分析方法，通过软件进行仿真，分析一侧δ室内的传递介质在20～70 ℃条件下，另一侧相对温度不变时，传递介质温度变化引起测量膜片的位移变形情况，得到不同温度下的测量膜片中心位移数据。将20 ℃的位移变化设定为0，并列出如表4所示的以10 ℃为增量，20～70 ℃的位移变化表。同时得到拟合公式(5)。

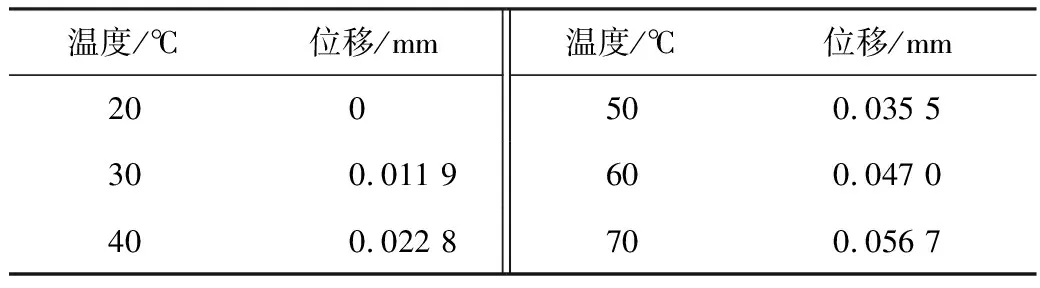
表4 温度-位移偏移变化表

y=1.19×10-3x-0.024

(5)

由表4和式(5)可见，预加张力44 MPa条件下的温度-位移变化成线性关系，斜率为1.19×10-3。以测量膜片位移作为分析度量指标，以预加张力44 MPa，20 ℃条件下的位移作为基准位移，分析温度对位移偏移影响，结合表4数据和式(5)可知，每10 ℃的温度变化，会引起大概1.19%的位移偏移。说明拟合公式的斜率可以作为偏移影响的一种度量，同时说明温度的大范围变化会导致较大的影响。

3.2 不同预加张力、不同温度下的位移变形分析

前文分析的是固定预加张力下、同温度的位移变形，在此基础上，通过调整预加张力的大小，进一步研究预加张力和温度变化对于测量膜片的影响。将预加张力以44 MPa为参考，分别取预加张力为0、18、26、53、70、88 MPa 加以分析，图10与表5分别是在分析一侧δ室内的传递介质在20～70 ℃的条件下对中心测量膜片产生的位移变形后，得到的温度-预加张力-位移图以及拟合数据得到的拟合公式表。同时建立如图11和表6所示，以10 ℃为增量，20～70 ℃的每种预加张力情况下测量膜片位移相对于预加张力44 MPa条件下的基准位移的偏移分布表和偏移分布图。选用位移偏移量ε分析位移精度情况。

表5 温度-预加张力-位移拟合公式

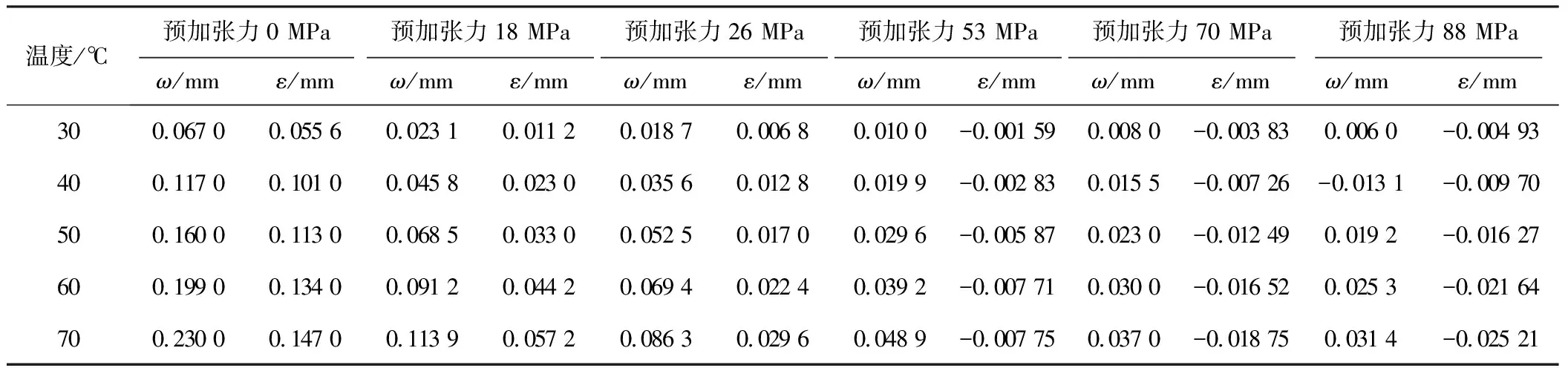
表6 不同预加张力条件下的温度-位移偏移量

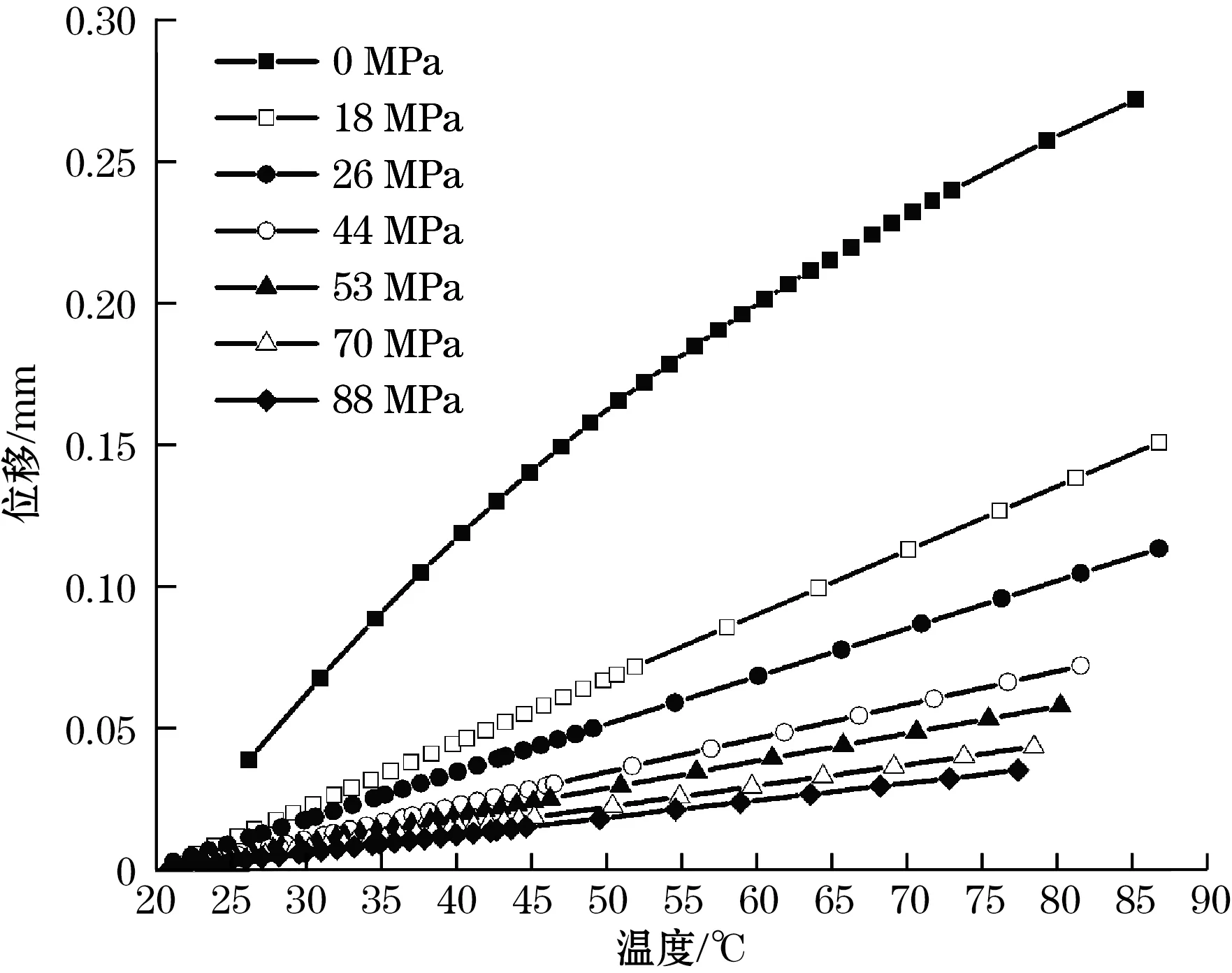
图10 温度-预加张力-位移拟合图

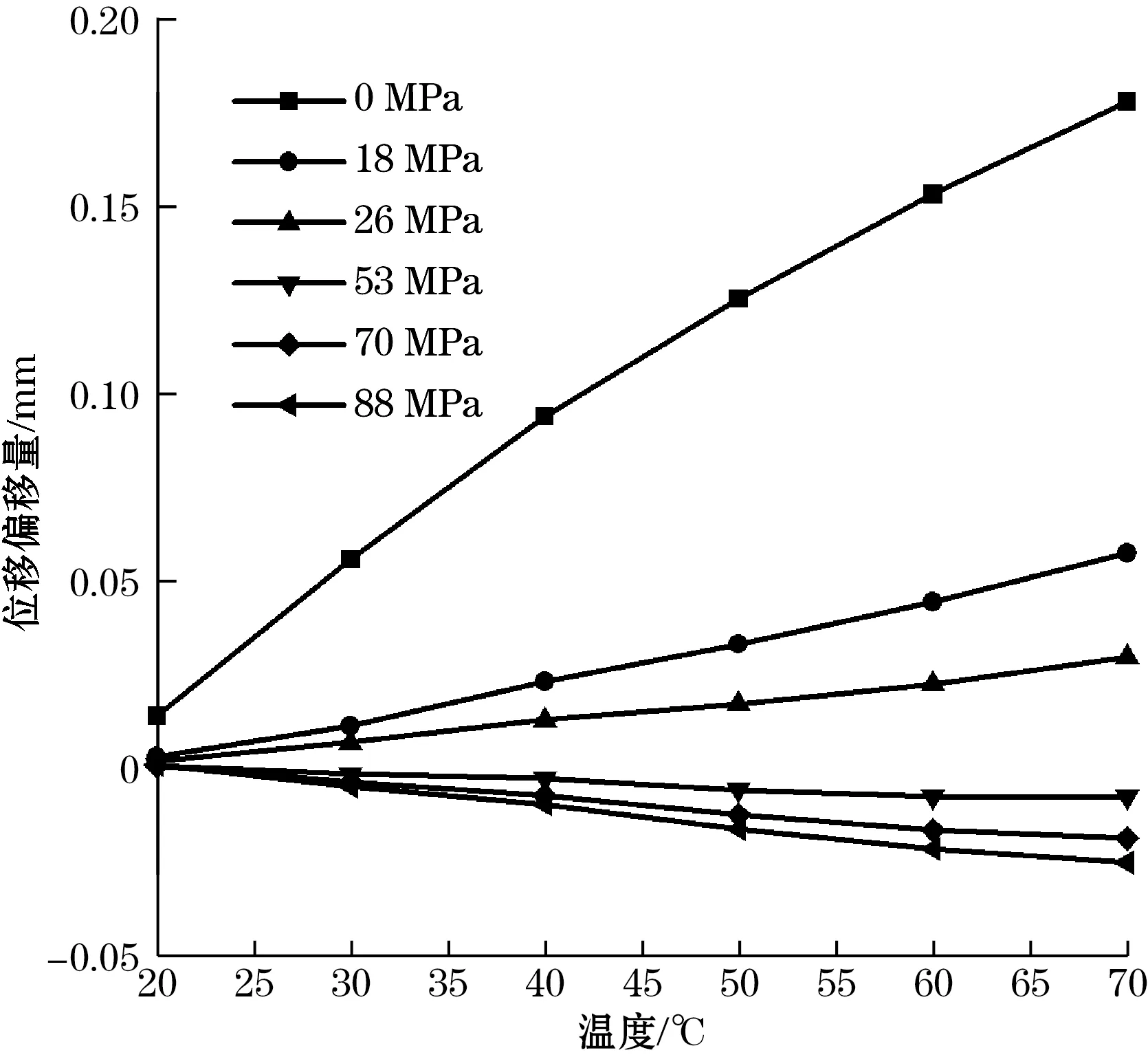
图11 不同预加张力的温度-位移偏移量图

ε=ωt-ω

(6)

式中：ωt为某预加张力条件下某温度对应的位移量；ω为预加张力44 MPa条件下与ωt相同温度对应的位移量。

通过表5和图10可见，预加张力为0MPa的测量膜片的温度-位移变形拟合公式为二次多项式形式，预加张力不为0MPa的测量膜片的温度-位移变形拟合公式都近似为线性关系，二者明显不同，说明给定预加张力可以让测量膜片的温度-位移变形具有线性关系。线性关系对于后续的温度位移偏移的处理十分有利。

由于不同的预加张力对应着不同的线性关系，也对应着不同的线性系数，结合线性系数的数学意义以及实际物理背景，线性系数可以认为是度量给定预加张力情况下测量膜片的温度-位移的一种灵敏度系数。因此预加张力的合理选择在测量膜片的设计和使用中十分重要。

表6和图11说明初始位移偏移相对来说较小，但是随着温度变化的增大，偏移的效果越来越明显，其中无预加张力情况和有预加张力情况在相同温度变化下引起的测量膜片位移变化十分明显。

当给定预加张力时，对温度和位移偏移数据进行分析并拟合，得到温度和位移偏移量的变化是线性关系，相关结果如表7所示，可以认为其中拟合公式的线性系数是温度-位移偏移量的一个度量指标，通过公式推导和数据分析，发现这个度量指标可以认为是上文中提到的给定预加张力与基准预加张力的两个温度-位移的灵敏度系数之差。

表7 温度-预加张力-位移偏移量拟合公式

图12为预加张力与位移偏移量的关系，当给定相同温度时，对预加张力与位移偏移量数据进行分析，发现随着预加张力的增大，位移偏移量随之减小，但是这种位移偏移量变化不是线性关系。当施加预加张力大于基准预加张力后，位移偏移量为负数，说明由于预加张力过大，导致位移变化量相较于基准量降低，实际表现为显示压力数值小于实际压力数值。

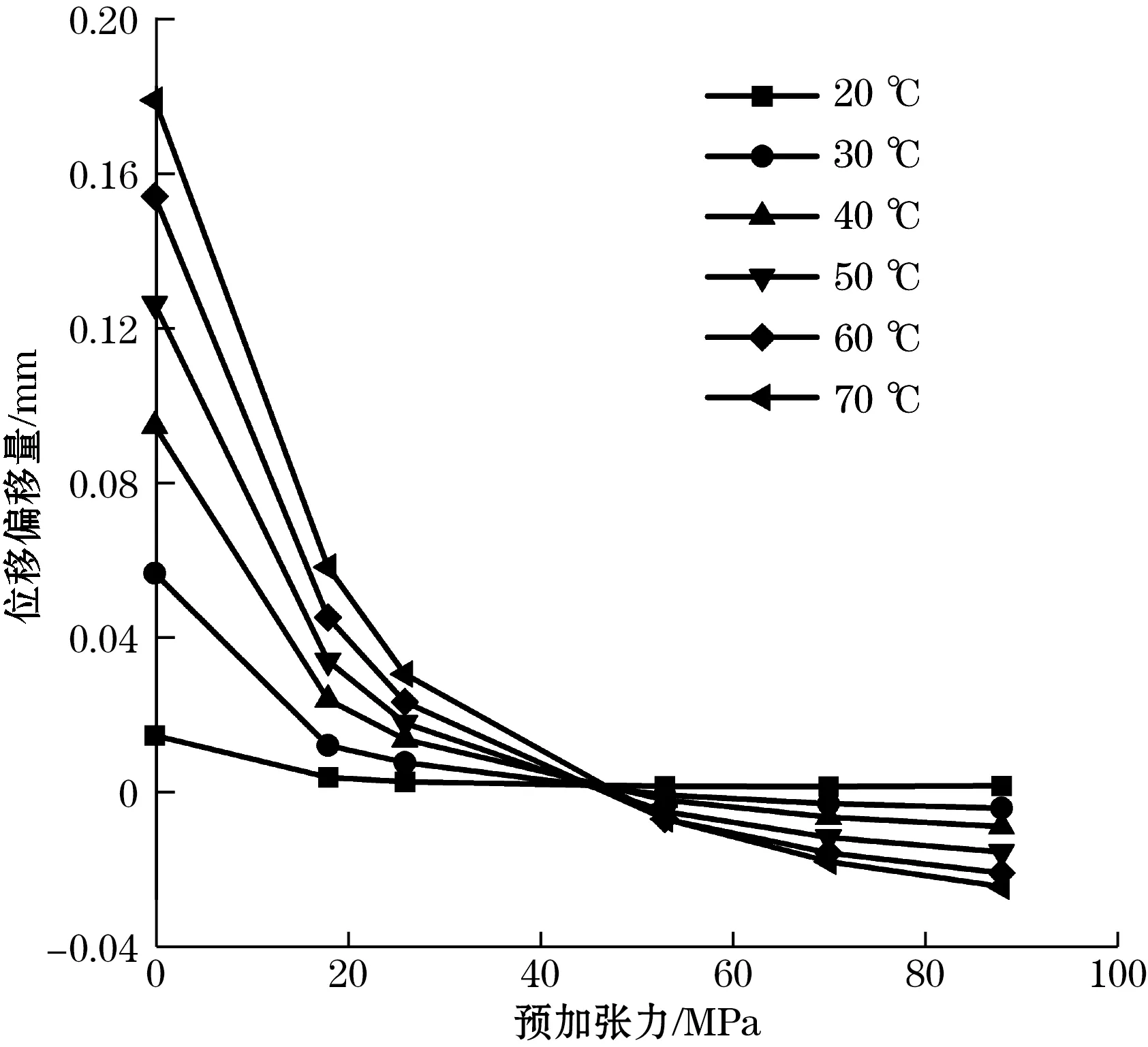
图12 不同温度的预加张力-位移偏移量图

3.3 预加张力与线性系数的分析

图13为预加张力与拟合公式线性灵敏度系数的关系，得到拟合公式为式(7)：

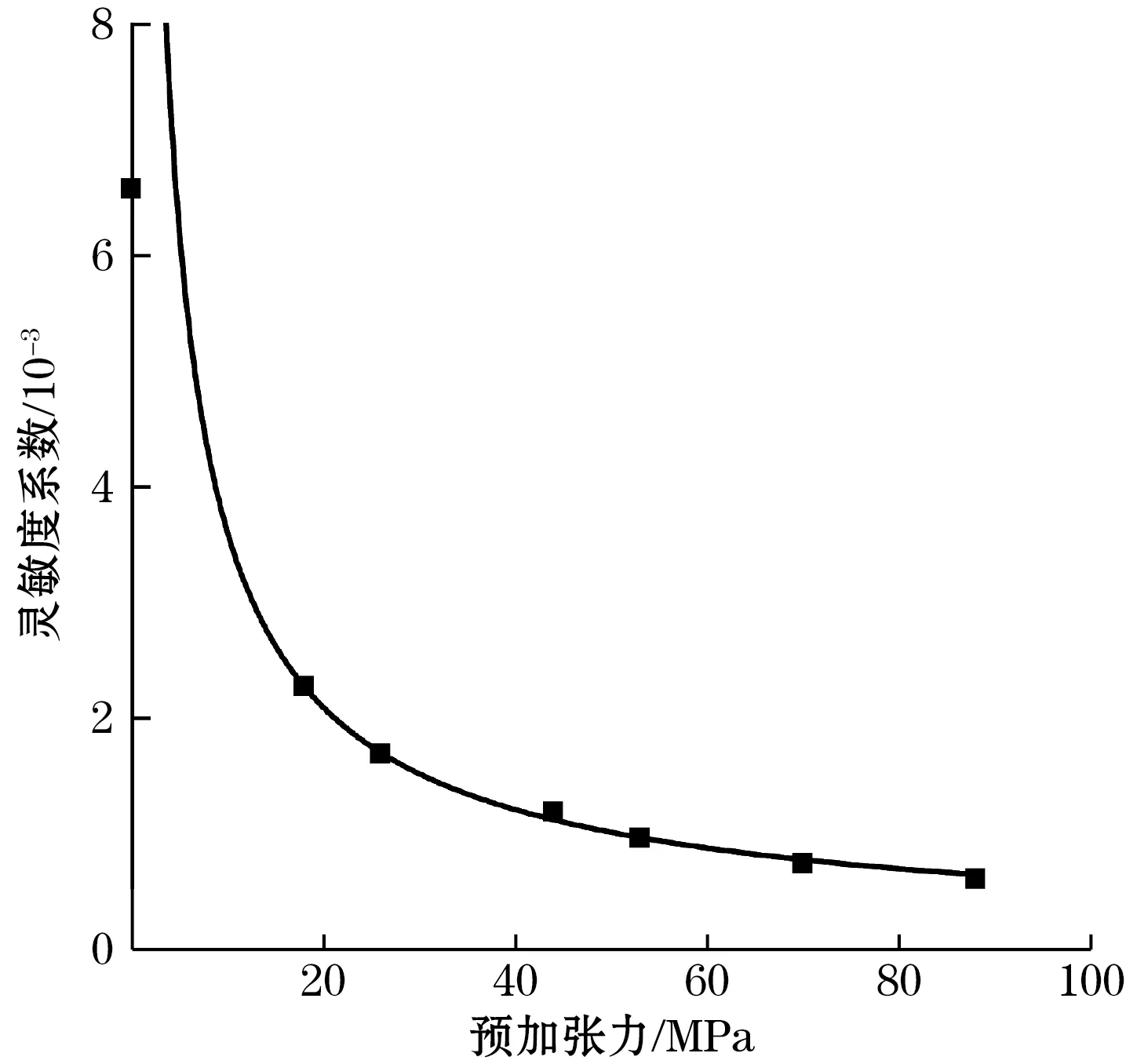
图13 灵敏度系数-预加张力关系图

y=22.6x-0.79

(7)

预加张力与灵敏度系数是一种幂函数关系，随着预加张力的增大，刚开始的灵敏度系数的降低是十分迅速的，但是后面灵敏度系数的降低十分有限，因此不能单纯通过调整预加张力来满足测量膜片对于不同灵敏度要求以及误差控制的要求，还需要其他的控制手段来实现实际使用要求。结合前文中对于给定预加张力情况下的温度-位移和温度-位移偏移量分析，可以得出，预加张力和温度对于位移的影响在于预加张力决定了位移变化的趋势；温度决定了位移变化的大小。

4 结论

本文通过对电容式压力变送器膜盒结构进行温度与预加张力分析，得到如下结论：

(1)无预加张力条件下，温度与测量膜片位移变化为二次曲线关系，有预加张力条件下，温度与测量膜片位移变化为线性关系。良好的线性关系能方便后续的温度-位移变化的处理，并且线性关系的系数可以认为是给定预加张力下的温度-位移变化的灵敏度系数。

(2)随着预加张力的增加，温度影响的位移偏移量ε明显降低。当预加张力固定时，温度与位移偏移量ε还是线性关系，此时的线性关系的系数可以认为是偏移量ε的度量，实际是两个温度-位移变化的灵敏度系数之差。但当温度采取某一定值时，预加张力与位移偏移量ε的关系不是线性关系。

(3)预加张力与线性灵敏度系数的关系为幂函数关系，开始时预加张力的微小改变会引起灵敏度的巨大变化，但是随着预加张力的增加，灵敏度的改变十分有限。预加张力决定了位移偏移量的趋势，温度决定了位移偏移量趋势的大小。

5 结束语

通过研究不同预加张力条件下温度对于位移变化的影响规律，可为以后的膜盒结构优化设计提供一定的参考，为合理选择膜盒预加张力大小以及后续电路环节进行温度补偿电阻的选择和补偿方法的设计提供参考和帮助，有助于降低温度产生的误差，从而提高设备的可靠性。