高频响MEMS石墨烯压力传感器设计

郑士瑜，侯 文，王俊强，范宏斌，吴天金，李孟委

(1.中北大学仪器与电子学院，山西太原 030051；2.中北大学前沿交叉科学研究院，山西太原 030051；3.中北大学信息与通信工程学院，山西太原 030051)

0 引言

爆破冲击波及航空航天发动机等动压测量场合，要求传感器具有高固有频率，耐高温特性，实现高温动态压力的精确测量。应用较广泛的高频响压力传感器主要是压阻式和压电式[1]。其中压电式压力传感器的固有频率高达100～400 kHz，无法满足μs量级与低频段压力信号的精准测量。传统压阻式压力传感器大多使用Si作为压力敏感单元，在超过120 ℃环境下使用时，会由于内部PN结出现漏电而导致传感器性能急剧下降，进而导致失效；被开发的替代品如碳化硅具有耐高温特性，但它们的微加工工艺还不够成熟[2]。石墨烯被认为是一种潜在的压阻材料，除了具有非常高的载流子迁移率外，还可以承受大的应变，石墨烯的电阻率随应变成线性变化，并在700 ℃的温度下保持稳定[3-5]，石墨烯材料已在国内外进行广泛研究[6-8]。

就芯片结构而言，上海交通大学、西安交通大学[9-10]研制的C型结构芯片，工艺简单，当该结构膜厚度较薄时，将造成传感器的非线性急剧增加[11]，在此基础上提出E型硅结构[12]，虽然降低非线性误差，但是以牺牲灵敏度或传感器尺寸为代价，此外，附加的中心质量会增加膜片的加速度灵敏度[13]。本文采用“硅膜+硅十字梁”结构进行设计，硅膜结构提升了结构刚度，另外十字梁结构具有应力集中效应[14]，能够更好地发挥石墨烯材料特性。

1 工作原理

本文提出的高频响石墨烯压力传感器结构如图1(a)所示，芯片结构主要包括上层“膜+凸柱” 与下层“十字梁”，“凸柱”结构恰好压在十字梁中心，利用金属键合技术使传感器芯片与封装外壳、芯片的上下两层紧密结合，完成传感器气密封装。压力介质通过传感器管壳上端开口作用在硅膜上表面，使膜片下方的凸柱带动十字梁结构向下产生位移，十字梁根部的石墨烯敏感膜片发生形变，如图1(b)所示，石墨烯能带结构产生带隙，影响载流子浓度及电子迁移率导致电阻发生改变。为了获得高灵敏度，十字梁上的4条电阻组成惠斯登电桥，处于应变最大区域。因此，由于外部压力作用，惠斯登电桥电路失去平衡，电阻变化转换为电压变化。

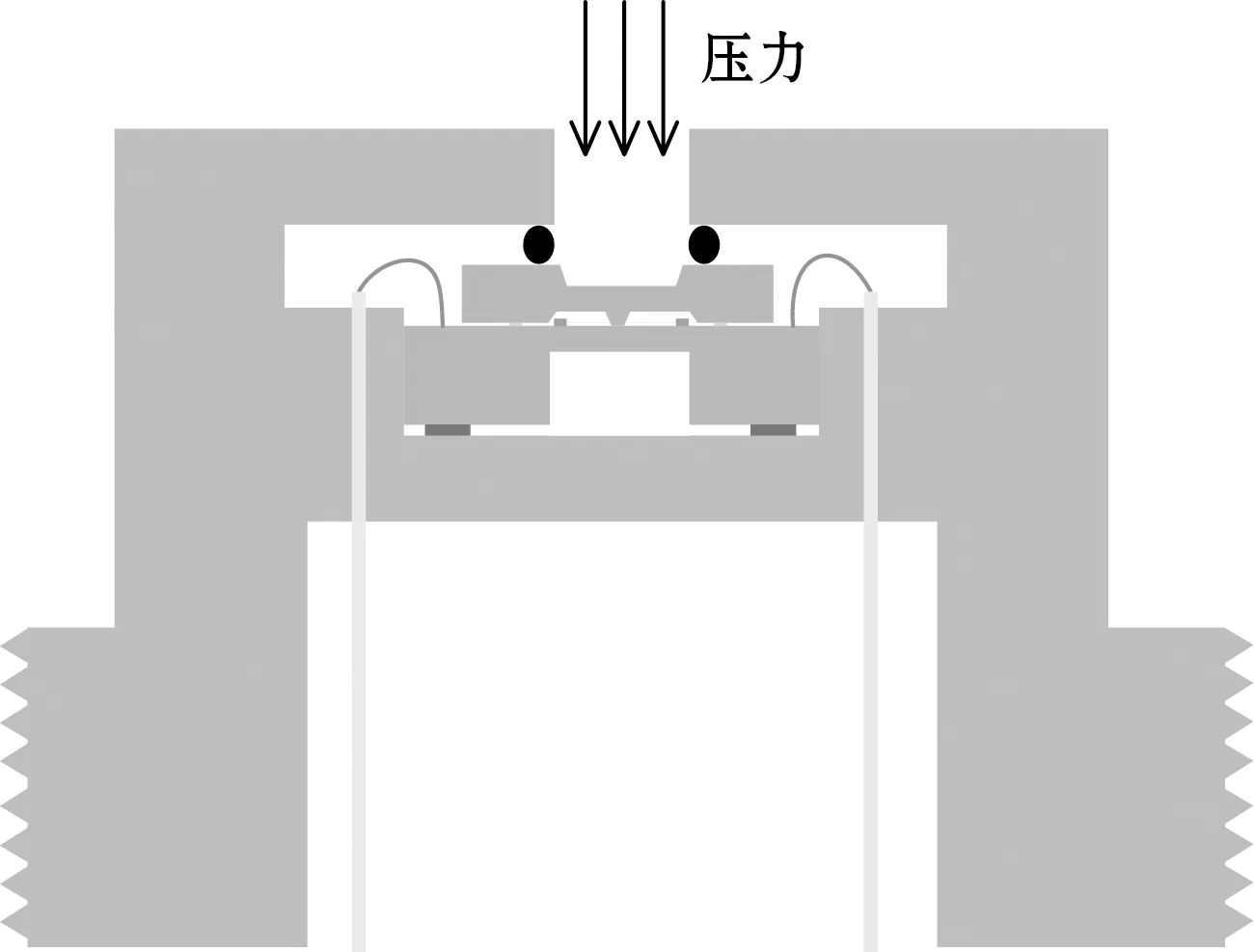
(a)整体结构示意图

1.1 硅的弹性常数

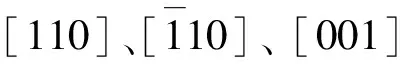
(1)

式中C为材料库中未经变化弹性常数矩阵。

根据广义胡克定律、切应力互等定理、坐标变换(弹性力学)公式，新坐标系下的弹性常数矩阵为C=ACAT，其中A为应力张量坐标变换矩阵，可表示为

(2)

式中：l、m、n为新旧坐标系的方向余弦，用矩阵β表示。

(3)

可得变换后的弹性常数矩阵C＇：

(4)

1.2 芯片主要结构与尺寸参数设计

本文设计压力传感器量程为表压0～60 MPa，芯片最大尺寸为4.5 mm×4.5 mm×0.8 mm。芯片双层结构的实现方法是：分别对2片厚400 μm、(100)晶面的单晶硅片，使用MEMS工艺加工中的湿法腐蚀、DRIE干法刻蚀形成。选用六方氮化硼(h-BN)作为石墨烯的防护层，h-BN已被广泛证实是石墨烯最佳的匹配材料，原因是石墨烯与h-BN垂直堆垛可形成范德华异质结，可以有效屏蔽其他衬底材料高低起伏等引起的声子和电荷散射等干扰[15-17]。石墨烯与h-BN在十字梁根部形成的异质结，与金属电极电学连接。上层、下层与封装外壳之间通过金属密封环形成密封结构，并充入氮气，使石墨烯处于无氧测量的环境中。

1.2.1 强度准则

由于单晶硅材料内部存在缺陷致使应力集中，导致屈服应力显著下降。根据相关文献[18]，在工程中常用的4种强度理论当中，使用Mises理论描述单晶硅的屈服强度，与实际材料的屈服强度最接近，在目前没有明确的描述脆性材料的失效准则，Mises理论无疑是最合适的。Von Mises理论可以简单地表示为：当材料内某一点的等效应力达到某一定值时，该点就进入塑性变形状态，等效应力可由式(5)表示。

(5)

单晶硅的屈服应力为6.0～8.3 GPa[19]，但材料内部缺陷、结构差异性、尺寸效应、MEMS工艺等因素会降低屈服应力，考虑到器件可靠性，设置屈服应力不宜过高。

1.2.2 硅膜结构设计

上层硅膜的设计参数主要包括硅膜的厚度h1、边长a。若假设凸柱为刚体，则可把该模型简化为超静定结构。其中，硅膜与十字梁结构共同承担压力，但硅膜因刚度较大，可承载绝大部分压力，考虑到结构安全性，故硅膜设计优先级要高于十字梁结构。图2为满量程下不同膜厚与边长下的Von Mises应力仿真结果，由图2可知，当边长a一定时，芯片的最大应力与膜厚成反比关系；当膜厚h1一定时，芯片的最大应力与边长成正比关系。

图2 不同膜厚h1下边长与最大应力关系

图3为不同膜厚h1下梁根部应变与边长a的关系。同样地，应变与膜厚h1和边长a的关系、应力与膜厚h1和边长a的关系一致。即应力越大，应变越大。

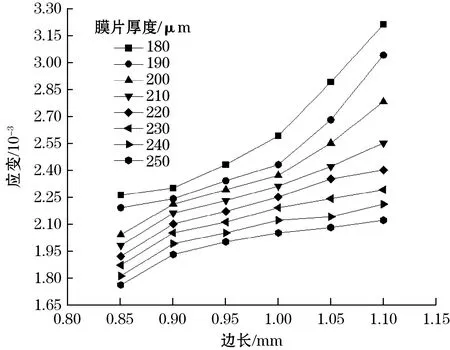
图3 不同膜厚h1下边长与应变的关系

1.2.3 十字梁结构设计

在确定上层硅膜结构尺寸之后，再对十字梁结构进行优化。图4为应力仿真云图。图5为不同梁厚下应力、梁根部应变曲线，由图5可知，随着梁厚h2的增加，最大应力逐渐变小，而应变呈先变大后变小的趋势，出现这种现象的原因是：十字梁越厚，下层结构刚度越强，承载能力越高，能够分担更多的压力，在上层膜片结构不变的情况下，这会导致上层的最大应力降低，而下层的应力增加，故曲线呈下降趋势；十字梁上应力增加，故应变升高，继续升高，也会因整体结构刚度增加导致应变减少，故应变曲线呈先增大后减小的趋势。当梁的厚度为110 μm时，施加60 MPa的压力载荷，此时梁根部应变最大，为0.259%，芯片最大Von Mises应力为890 MPa。

图4 梁厚为110 μm时的应力仿真云图

图5 梁厚h2与最大应力、应变关系曲线

传感器整体的高频测量范围是由谐振频率决定的，而影响谐振频率的主要因素为芯片的固有频率[20]。最后，对芯片进行模态分析，仿真的一阶固有频率为1.34 MHz，且振动方向与被测压力方向平行。

2 传感器工艺设计

2.1 十字梁结构加工工艺流程

(1)对400 μm、(100)硅片进行清洗烘干。

(2)利用光刻掩膜技术磁控溅射技术在硅片表面生长Cr/Au 15/50 nm的电极，在芯片背部溅射Cr/Au 50/200 nm。

(3)利用深硅刻蚀技术，刻蚀出深290 μm方腔结构。

(4)在芯片上表面转移下层BN石墨烯，利用光刻掩膜技术进行图形化；将转移并刻蚀之后的BN芯片上转移石墨烯并刻蚀图案，之后转移第二层BN进行覆盖并刻蚀图案。

(5)将转移好的芯片在BN/Gra/BN敏感结表面生长150 nm SiNx，再对表面进行部分刻蚀露出电极，在刻蚀部位表面再生长一层Cr/Au，将电极抬高。

(6)利用磁控溅射技术、电子束蒸发工艺在上表面形成金属密封环，用于上层结构键合。

(7)利用深硅刻蚀技术形成十字梁。

2.2 上层硅膜与凸柱加工工艺流程

(1)使用稀HF酸清洗硅片去除表面氧化层后，清洗，再使用KOH溶液，腐蚀形成上、下层方腔与凸柱。

(2)在底面进行金属溅射形成密封环。

最后，将分割好的芯片金属键合完成芯片制作。上述所有简化步骤流程如图6所示。

3 石墨烯电阻值设计

总电阻Rt由电极电阻Re，接触电阻Rc与石墨烯薄膜电阻Rg组成，即Rt=2Rc+Re+Rg，Rg可根据薄膜材料电阻计算公式Rg=ρl/W计算，其中ρ为二维材料石墨烯电阻率，l与W分别为长度与宽度，也可以根据方阻计算公式计算。常用的石墨烯电极材料有Ni、Au、Pd、Pt等，也可以是上述材料的两种的组合，接触电阻的大小取决于石墨烯中的狄拉克点能量[21]，并与MEMS工艺、接触金属材料有关，约为几百到几千Ω·μm，通常通过实验测得。本文设计的石墨烯电阻尺寸如图7所示，石墨烯方块电阻取1 109 Ω/□[22]，忽略电极电阻大小，并取接触电阻为90 Ω，粗略计算得到总电阻Rt为5.725 kΩ。

图7 电阻组成示意图

4 结束语

设计了一种膜+梁结构石墨烯高频响压力传感器，在各向异性算法下，对该结构进行了静、动力学仿真研究，一阶固有频率为1.34 MHz，在60 MPa的压力下，最大应力为890 MPa，远小于材料屈服强度，最大应变为0.259%，同时设计了石墨烯的电阻值，对未来石墨烯器件设计提供了一定指导作用。