新型蓄热体结构蓄热过程分析

胡自锋，徐耀祖，段振云，商向东，徐景久

（1沈阳工业大学机械工程学院，辽宁 沈阳 110870；2沈阳华维工程技术有限公司，辽宁 沈阳 110180）

为改善环境问题和节约能源，国家实施了“碳中和、碳达峰”的绿色零碳政策，大力推广“煤改电”，提倡清洁能源利用。固体蓄热技术在实现节能减排和电网的削峰填谷中发挥着重要作用。固体蓄热是一种利用夜间低谷电将电能转化为热能存储于蓄热体中，在需要提供热量时再进行热能释放的蓄热方式[1-3]。

现阶段对固体蓄热技术的研究中，胡思科等[4-5]通过对氧化镁固体蓄热模型的仿真分析，得出在达到稳定状态时，具有圆形孔道的蓄热体较方形孔道的蓄热体蓄热时间要短，且孔数越多时间越短的结论。鞠亮亮等[6]以氧化镁耐火砖作为蓄热单元，对高温耐火砖的孔道形状及排布进行研究，得出不同宽高比和不同长短半轴比值的矩形和椭圆形孔道耐火砖的蓄热性能。徐耀祖等[7-8]对传统蓄热装置的蓄热体结构进行研究，提出一种能提高蓄热量的截面和功率分布复合优化方式。

针对现有固体蓄热技术存在的蓄热体局部受热不均及实际蓄热能力偏低等问题，基于现有理论研究成果，本工作结合实际工程应用对固体蓄热器的蓄热体结构进行设计分析，建立一种新型结构蓄热体，利用ANSYS Workbench模块下的Steady-State Thermal和Transient Thermal对建立的新型结构蓄热体与传统结构蓄热体进行对比研究，得到两种蓄热体结构在相同蓄热时间下的温度分布规律和目标蓄热温度下的实际蓄热能力[9]。

1 蓄热体模型构建

1.1 结构模型

目前市面上大多数固体蓄热器其内部蓄热体结构的搭建均采用一种固定的蓄热砖进行堆砌，砖体结构单一。蓄热体传统结构的砖体结构图及蓄热体结构模型如图1、图2所示，单块MgO砖尺寸230 mm×114 mm×65 mm，蓄热体尺寸L：1.15 m、W：1.38 m、H：1.11 m，蓄热孔尺寸97 mm×65 mm。由于传统结构蓄热体蓄热孔多为MgO 砖堆砌而成的矩形通道，矩形蓄热孔横纵方向对齐排列，但横向蓄热孔与纵向蓄热孔间堆砌的MgO砖层数不同，则电阻丝对蓄热孔周围各层MgO砖的加热距离不等，易导致蓄

图1 砖体传统结构图Fig. 1 Traditional structure of the brick body

图2 蓄热体传统结构模型Fig. 2 Traditional structure model of heat storage

热体温度分布不均，产生较大温度梯度，局部温度过高将会缩短电阻丝使用寿命，增加设备后期维护成本。

考虑到传统结构蓄热体的蓄热孔为堆砌形成，壁面接触会形成热阻，新型砖体蓄热孔采用直接加工成型的方式，消除壁面接触热阻的影响；为解决电阻丝对蓄热孔周围砖体加热距离不等的问题，同时考虑蓄热体结构搭建稳定性，新型砖体采用正六边形结构，圆形蓄热孔位于正六边形中心。砖体结构如图3所示，最小蓄热单元MgO砖截面形状为正六边形，边长95 mm，砖体中心设有直径为65 mm的蓄热孔，用于放置电阻丝加热蓄热体，砖体厚度为230 mm。

图3 砖体结构示意图Fig. 3 Diagram of the brick body structure

本工作提出的新型蓄热体结构砖型排布如图4所示，使用3种不同砖型搭建蓄热体，相邻2种砖层之间错缝排布。搭建完成的蓄热体结构如图5所示，蓄热体顶部与底部分别放置有填充砖与固定板，以保证蓄热体受热稳定性，蓄热体尺寸W：1.33 m、L：1.20 m、H：1.07 m，蓄热孔尺寸1150～65 mm，3种砖型MgO 砖共120 块，由蓄热体结构决定其蓄热孔数量为54。

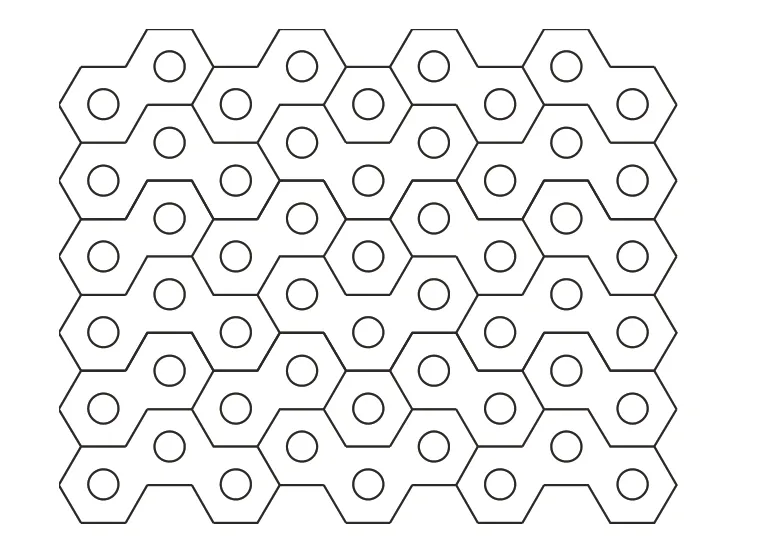
图4 砖型排布图Fig. 4 Layout diagram of brick type

图5 蓄热体结构模型Fig. 5 Heat storage structure model

1.2 数学模型

结合蓄热过程的传热学理论及蓄热体结构特点，对蓄热过程分析模型作如下处理：①忽略蓄热体内部MgO砖间的面接触热损失，蓄热体外壁面作绝热处理，与环境没有热量交换；②忽略辐射换热，用壁面热传导代替；③考虑到蓄热体纵向分布一致性，故取蓄热体模型的1/10进行蓄热分析。

该蓄热体的蓄热过程属于具有内热源Φ̇的三维非稳态导热，考虑物理参数非线性，其微分方程为[10]：

式中，ρ为镁砖密度，kg/m3；c为比热容，J/(kg·K)；t为时间，s；λ为导热系数，W/(m·K)；Φ̇为内热源生成热，W。

由于蓄热介质MgO砖的热物理参数随温度、蓄热时间等影响较大，采用定值处理进行蓄热分析易产生仿真误差，故此处采用非定值仿真分析方法。在非定值处理的各参数中，密度几乎不随固体材料的温度变化而变化，通过Solidworks模型质量属性读取标砖实际体积以及称重法测量得到MgO砖实际密度ρ为2796 kg/m3。MgO 砖比热容、导热系数与温度的关系，通过Origin软件进行二次函数拟合可得[11]：

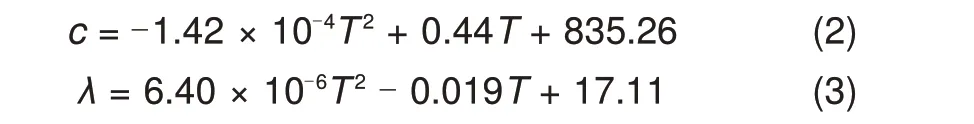
式中，c为比热容，J/(kg·K)；λ为导热系数，W/(m·K)；T为热力学温度，K。

2 蓄热过程对比分析

本工作利用ANSYS Workbench 模块下的Steady-State Thermal和Transient Thermal分析方法对新型结构蓄热体与传统结构蓄热体的蓄热过程进行对比仿真分析。两种蓄热体结构数值模拟对比分析中，设计蓄热时间10 h，蓄热起始温度373 K，蓄热终止温度873 K。根据传热学理论可算出两种蓄热体结构的理论蓄热容量，再通过数值模拟结果，即可对两种蓄热体结构的实际蓄热量、蓄热时间及温度分布情况进行对比分析。

2.1 无关性验证

在对模型进行网格划分时，需要确定计算所用网格的网格数量以及时间步长与计算获得的结果之间无关联性，也就是要进行网格无关性验证和步长独立性验证。两种蓄热体模型对应的网格划分数量及步长划分见表1、表2。

Pancreatic fibrosis is the characteristic feature of chronic pancreatitis and pancreatic ductal adenocarcinoma. Revealing desmoplasia at an early stage can be a useful diagnostic tool.

表1 网格划分Table 1 Grid partitioning

表2 步长划分Table 2 Time step partitioning

通过对蓄热过程的数值模拟，得到两种蓄热体结构在不同网格数及步长下物理模型平均温度随时间的变化曲线如图6所示。

从图6可以看出，不同网格划分数及不同步长设定下，两种物理模型数值模拟结果的平均温度随时间变化曲线基本重合，网格数增加和步长缩短对数值模拟结果影响不大。为提高计算效率，在满足计算精度的情况下，本工作选取传统结构蓄热体网格数72028，新型结构蓄热体网格数183001，时间步长600 s进行蓄热过程数值模拟分析。

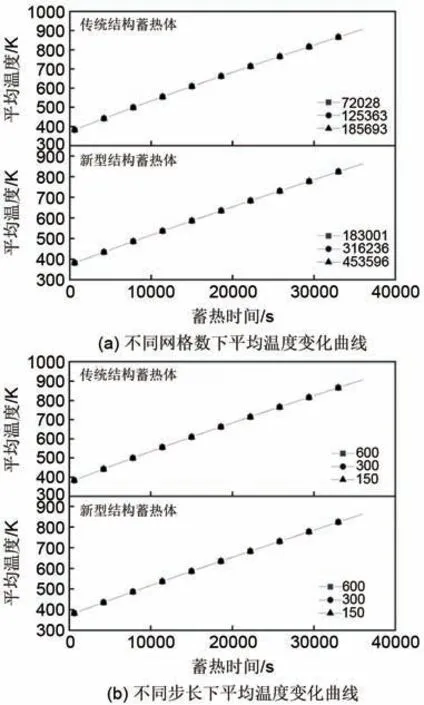
图6 物理模型平均温度变化曲线Fig. 6 Average temperature curve of physical model

2.2 蓄热温度对比分析

蓄热容量指单位体积(或质量)下，蓄热体热储存容量，计算公式为：

式中，Q为蓄热容量，kWh；v为蓄热体积，m3；c为介质比热容，J/(kg·K)；Δk为蓄热温差，K。

设计蓄热时间10 h，蓄热温差500 K，结合蓄热体体积参数，根据式(2)、(4)即可得出两种蓄热体结构的理论蓄热容量及单孔加热功率值。传统结构蓄热体与新型结构蓄热体相关参数对比见表3，其中总砖隙比为：蓄热砖总体积/蓄热孔总体积。

表3 对比分析参数表Table 3 Comparative analysis parameter table

首先对两种蓄热体结构进行定容比较分析，由于两种蓄热体结构不同，则通过公式计算得到的理论蓄热容量不同，但两种蓄热体结构的设计蓄热时间及蓄热温差相等，所以可根据理论蓄热容量计算结果，设定传统与新型蓄热体结构模型的蓄热功率分别为6.26 kW 和5.60 kW，蓄热功率平均分布到各个蓄热孔内热源加热蓄热体。最终得到两种蓄热体模型目标蓄热10 h 时的温度分布情况如图7 所示。KⅠ～KⅥ与K1～K7分别为传统结构蓄热体与新型结构蓄热体分析模型的模拟温度监测点。

从图7 中可以看出，两种蓄热体结构在蓄热10 h后的温度分布云图区别明显，图7(a)中传统结构蓄热体温度分布梯度较大，温度分布以蓄热体中心点为核心呈面性递减，整体温差值为227.0 K；图7(b)中新型结构蓄热体温度分布以横向轴线呈线性递减，整体温差值为107.8 K。

图7 蓄热10 h温度分布对比图Fig. 7 Temperature comparison diagram for a 10-hour heat storage

传统结构蓄热体与新型结构蓄热体不同时间的监测点温度值见表4、表5。其对应的监测点温升曲线如图8所示。

表4 传统结构蓄热体节点时间温度分布Table 4 Node time temperature distribution of conventional structural heat storage body

表5 新型结构蓄热体节点时间温度分布Table 5 Node time temperature distribution of the new structure heat storage body

图8 监测点温升曲线Fig. 8 Temperature rise curve of monitoring points

通过对两种蓄热体模型温度监测点数据分析可知，传统结构蓄热体6个监测点中靠近蓄热体中心区域的KⅡ、KⅢ、KⅤ温度值和温升曲线在蓄热初期重合度较高，随着时间的推移，曲线重合度降低，而处于蓄热体外围区域的KⅠ、KⅣ、KⅥ温度偏差率达到12.3%；新型结构蓄热体7个监测点中整个蓄热体中部的K1～K4、K6点温度值和温升曲线在蓄热全过程基本一致，处于蓄热体外围区域的K5、K7温度偏差率仅为6.6%，相比于传统结构蓄热体，各个监测点的温升趋势更加接近。

图9为蓄热10 h传统结构蓄热体与新型结构蓄热体各温度段的网格节点温度分布占比图。

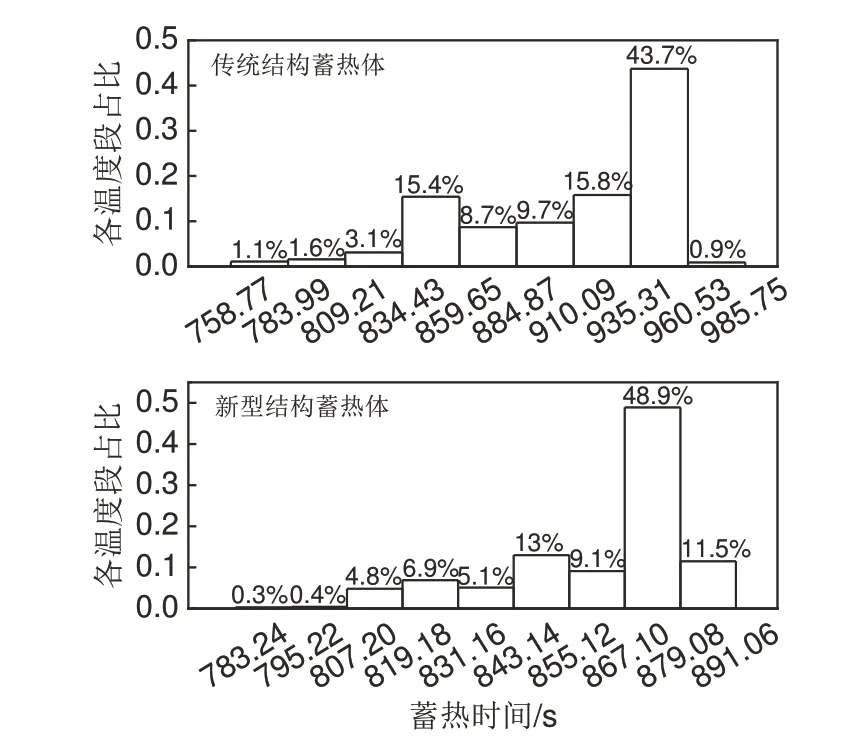
图9 节点温度分布占比图Fig. 9 Proportion diagram of node temperature distribution

由图9可以看出，蓄热10 h时传统结构蓄热体的节点温度在设计蓄热温度873 K附近的859.65～884.87 K区间占比仅为8.7%，而在高温段884.87～985.75 K区间占比达到70.1%，整体温度分布不均，局部温度过高会使温度传感器提前控制电阻丝停止加热，缩短蓄热体蓄热时间，则会影响整个蓄热体的蓄热容量；新型结构蓄热体的节点温度主要集中分布在设计蓄热温度873 K附近的867.10～891.06 K区间内，占比达到60.4%，未形成明显的高温段，整体温度分布更加合理，蓄热体蓄热时间更长，实际蓄热能力更好。

2.3 蓄热容量对比分析

结构改善后的新型结构蓄热体，蓄热孔内电阻丝对MgO砖的加热更加充分，其相应的蓄热时间及理论热容率将得到提升，当蓄热体达到目标蓄热温度时，蓄热体内布置的传感器控制电阻丝停止加热，结束蓄热过程。图10为两种蓄热体结构在相同边界条件下的蓄热过程温升曲线。

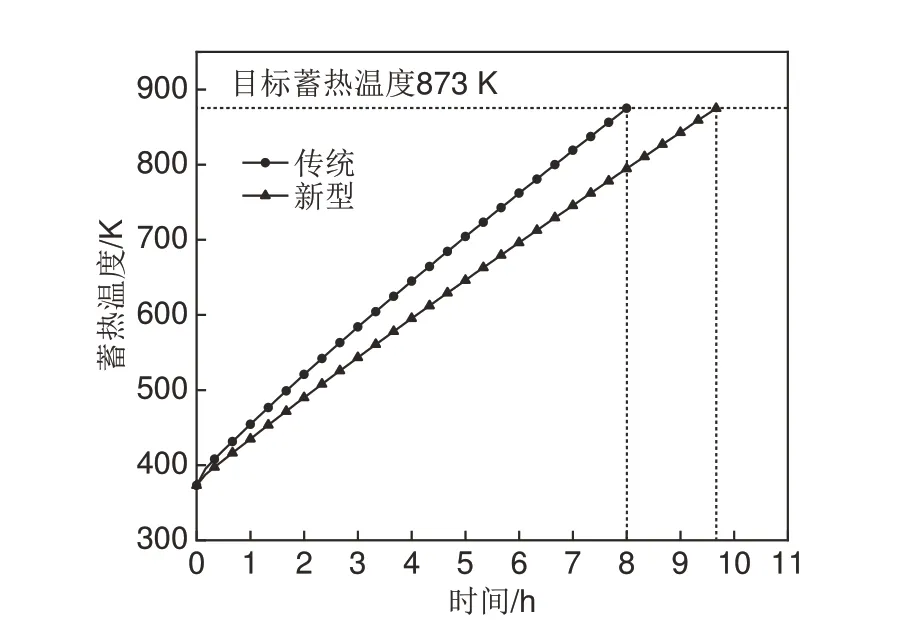
图10 蓄热过程温升曲线Fig. 10 Temperature rise curve of heat storage process

从图10可以看出，在相同目标蓄热温度下，传统结构蓄热体的蓄热时间为8.0 h，而新型结构蓄热体的蓄热时间为9.6 h，结合蓄热过程两种蓄热体模型设定功率值可知，新型结构蓄热体的实际蓄热能力更好。

表6为两种蓄热体结构达到目标蓄热终止温度873 K时的相关参数对比。

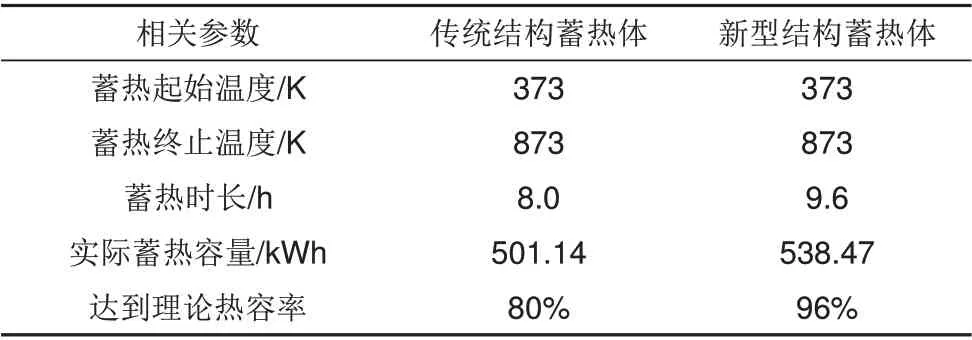
表6 终止温度873 K参数对比Table 6 Comparison of end temperature 873 K parameters

从表6可以看出，达到目标蓄热终止温度873 K时，新型结构蓄热体的实际蓄热容量达到理论蓄热容量的96%，而传统结构蓄热体的实际热容量仅有其理论热容量的80%。结合蓄热体结构参数分析，新型结构蓄热体单位体积蓄热容量提升了20%，即在相同的蓄热容量情况下，体积仅有传统结构蓄热体的83%，能有效减少蓄热体占地面积，提高资源利用率，相应减少用户初安装成本，有利于市场推广。

3 结 论

本工作以碱性耐火材料MgO砖作为蓄热介质，设计一种新型结构蓄热体，通过对两种蓄热体结构在相同蓄热时间下的温度分布规律和目标蓄热温度下的实际蓄热能力进行对比分析，得到以下结论。

（1）目标蓄热时间下，传统结构蓄热体整体温差值为227.0 K，监测点温度偏差率达12.3%，节点温度在高温段占比达70.1%，设计蓄热温度873 K温度段占比仅8.7%；新型结构蓄热体整体温差为107.8 K，监测点温度偏差率为6.6%，节点温度在设计蓄热温度873 K温度段占比60.4%，未形成明显高温段，整体温度分布更加合理。

（2）目标蓄热温度下，新型结构蓄热体的实际蓄热容量达到理论蓄热容量的96%，较传统结构蓄热体提升16%，同时体积仅有传统结构蓄热体的83%，能有效减少蓄热体占地面积，相应降低蓄热成本，有利于市场推广。