基于LBM的多孔介质无机复合相变材料储能特性
崔婷婷,王 燕
(南京工业大学机械与动力工程学院,江苏 南京 211816)
随着社会进步和现代工业的不断发展,能源短缺和环境污染问题开始不断显现。作为巴黎协议的签署国,中国是世界上最大的二氧化碳排放国,目标是在2030 年之前达到二氧化碳排放量的峰值,并力争2060年实现碳中和[1]。相变储能技术是提高能源利用率和节能减排的重要技术手段[2],相变材料(PCM)具备相变潜热大,储热效率高等优点,其中无机水合盐具有热物理性质优异[3]、来源广泛和价格低廉等优点被广泛应用于太阳能储热、绿色建筑、电子设备热管理等领域[4]。
PCM 具有较低的导热系数,目前提高导热系数的方法主要有增加肋片[5]、添加多孔介质[6]、纳米颗粒[7]等,其中多孔介质具有较高的导热系数和较大的传热比表面积,可以显著提高PCM 导热性能和整体传热性能,从而强化传热,因此国内外不少学者对其进行了研究。田伟等[8]、Li 等[9]和Wang等[10]均通过实验对添加金属泡沫的复合相变材料(CPCM)蓄热特性进行探究,结果表明,添加金属泡沫明显提高了CPCM 传热速率,缩短了CPCM熔化时间。在数值模拟方面,格子玻尔兹曼方法(LBM)在含多孔介质的相变储能特性研究分为表征体单元(REV)尺度和孔隙尺度。在REV 尺度上,Liu 等[11]建立了多孔介质中单相和固液相变传热的三维多重弛豫时间(MRT)LBM模型,结果表明,三维双分布函数(DDF)-MRT 多孔介质对流换热模型在空间上具有二阶精度。在孔隙尺度上,贾兴龙等[12]对方腔内填充不同梯度金属骨架结构系统的蓄热特性进行数值模拟研究,结果表明,正梯度骨架结构对相变换热过程的强化效果最好。四参数随机生长法(QSGS)因其简单、灵活和高质量的生成结构等优点,被用来重建骨架微观结构。Huo等[13]建立了PCM/多孔介质电池热管理(BTM)的LBM 模型,研究了瑞利数(Ra)和孔隙度(ε)对BTM 传热过程的影响,结果表明,降低ε会加快熔化速度。Han 等[14]建立熔融CPCM 的LBM 模型,结果表明,金属颗粒的存在提高了PCM 的热性能。焓法模型和温度法模型是研究相变传热过程的两种模型,而焓法模型在界面移动的问题上不需要时刻追踪移动的界面。Jourabian等[15]基于焓的DDF-LBM研究了多孔基质对环形区域冰融化的影响,结果表明,提高多孔基体的导热率或降低多孔基体的ε熔融速率都会增加。Ren等[16]采用焓的浸没边界LBM对金属泡沫增强PCM 熔融过程进行研究,结果表明,存在最佳的泡沫金属ε(0.95)以实现最高潜热储能装置的储能效率。
从上述研究发现,多孔介质增强了PCM 的储能效率。QSGS重构的多孔介质与实际多孔介质的骨架形貌符合性更高,因此目前国内外学者采用QSGS对随机分布多孔介质的相变储能机理进行研究,以往与多孔介质CPCM储能特性相关的数值研究大多为石蜡等有机PCM,基于LBM 在无机水合盐方面的研究较少,且QSGS重构的多孔介质大多数集中在研究其ε和骨架导热系数对相变传热的影响,而在孔隙尺度下探究骨架形貌对PCM 的相变储能影响几乎没有,因此本工作采用QSGS构造多孔介质无机复合相变模型对其相变储能机理进行研究,分析其ε、固相生长核分布概率(Pc)、方向生长概率(Pd)和Ra对相变过程的影响。
1 数值模型及计算方法
1.1 物理模型及控制方程
图1所示为二维方腔随机多孔介质无机CPCM的物理模型,方腔内充满ε为0.90的多孔介质骨架(黑色)和无机水合盐PCM(白色),其物性参数如表1 所示。当时间τ>0 时,无量纲熔化温度Tm=0.40,左壁面为高温壁面,无量纲温度Th=1,右壁面和上下壁面均为绝热壁面,无量纲温度Tc=0,模拟遵循以下假设:①多孔介质和PCM 的热物性参数均视为常数;②液体PCM 假定为不可压缩牛顿流体;③流体在壁面上满足无滑移边界条件;④多孔介质和PCM处于局部非热平衡状态。

表1 PCM和多孔骨架的物性参数[3]Table 1 Physical parameters of PCM and porous framework[3]

图1 物理模型Fig. 1 Physical model
基于以上假设,孔隙尺度内相变过程的连续性方程、动量方程和能量方程如下[14]:

式中,下标f、m 分别代表PCM、多孔骨架,u、T、p分别为液相的流速、温度、压力,Tref为参考温度,v、β、k分别为流体运动黏度、热膨胀系数和导热系数,cp、fl、L分别为定压比热容、PCM的液相体积分数和相变潜热。
在式(3)中,fl、L和T的关系可通过焓法求解,焓的定义为:

1.2 LBM模型
本工作采用DDF 的热LBM 模拟方腔内随机多孔介质无机CPCM的速度和温度场。
速度分布函数演化方程:

式中,τf为无量纲松弛时间,feqi为平衡态分布函数:

式中,τT,f、τT,m为无量纲松弛时间。
孔隙尺度下的多孔介质无机CPCM固液相变过程需要考虑流固耦合传热,本工作将固体的扩散系数设置为流体扩散系数的10 倍,并在固液界面采用反弹格式,固体上的粒子速度分量设置为0。
1.3 模型及网格无关性验证
为了验证LBM 模型的正确性,建立相似模型并与Beckermann 等[17]的实验结果相对比,图2(a)展示了不同时刻固液相界面的位置,从图中可以看出,本工作所建立的数值模型与Beckermann所做实验测试结果吻合较好,最大误差为4.05%,在误差允许范围内,因此可以证明本工作所建模型的可靠性。为进一步验证LBM 模型的准确性,构建Mencinger[18]所用模型并与其模拟结果进行对比,无量纲参数Ra设定为25000,对比结果如图2(b)所示,Nuave和fl的误差分别为1.83%和2.51%,再次验证了本模型的准确性。

图2 模型验证Fig. 2 Model validation
选用50×50、100×100、150×150 三种不同均匀网格进行网格无关性检验。不同网格数量对CPCM熔化过程中液相体积分数随傅里叶数(Fo)变化关系如图3所示。从图中可以看出,不同网格数量对CPCM液相体积分数的影响极小,曲线相差不大,因此综合考虑数值计算中的精度和速度,网格数量选为100×100。
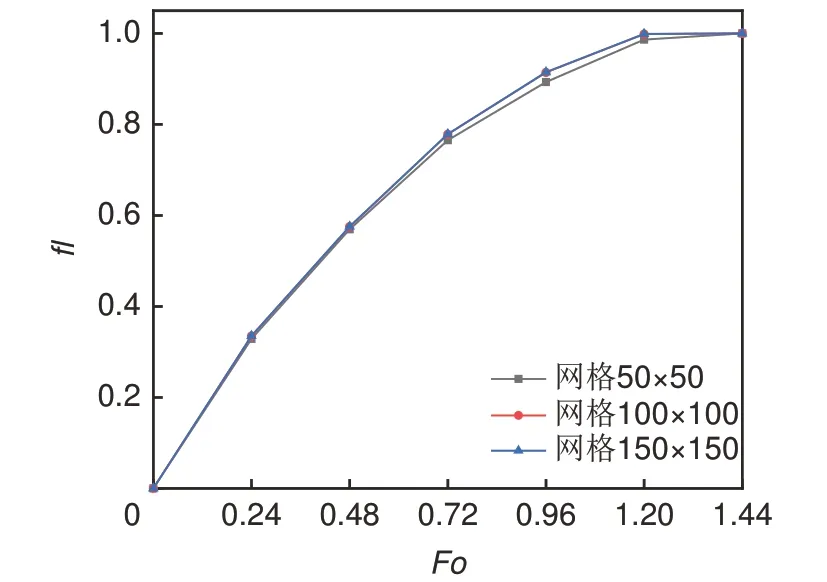
图3 网格独立性验证Fig. 3 Grid independence verification
2 数值模拟结果与分析
2.1 骨架ε的影响
为了研究ε对相变储能特性的影响,构建6 种不同ε(0.95、0.90、0.85、0.80、0.75、0.70)的二维方腔相变模型,在左壁面无量纲温度Th=1 的加热条件下探究ε对CPCM熔化过程的影响。Fo用于表示时间步长。图4展示了Fo=0.72时,ε为0.90、0.80、0.70的CPCM液相分布云图。在图4中,黄色部分表示已熔化的PCM,蓝色部分表示骨架与未熔化的PCM,骨架只导热不会发生相变。从图4中可以看出,随着ε的减小,PCM未熔化区域逐渐减少,这一方面是因为骨架的导热系数大于PCM的导热系数(10倍),使得热量的传导更为迅速,骨架右侧PCM 熔化速度加快,因此整体CPCM 熔化速度加快;另一方面是因为随着ε减小,多孔骨架含量增大,相应的PCM 减少。基于以上分析得出结论,多孔介质骨架的增加有效增强了CPCM的熔化速率。
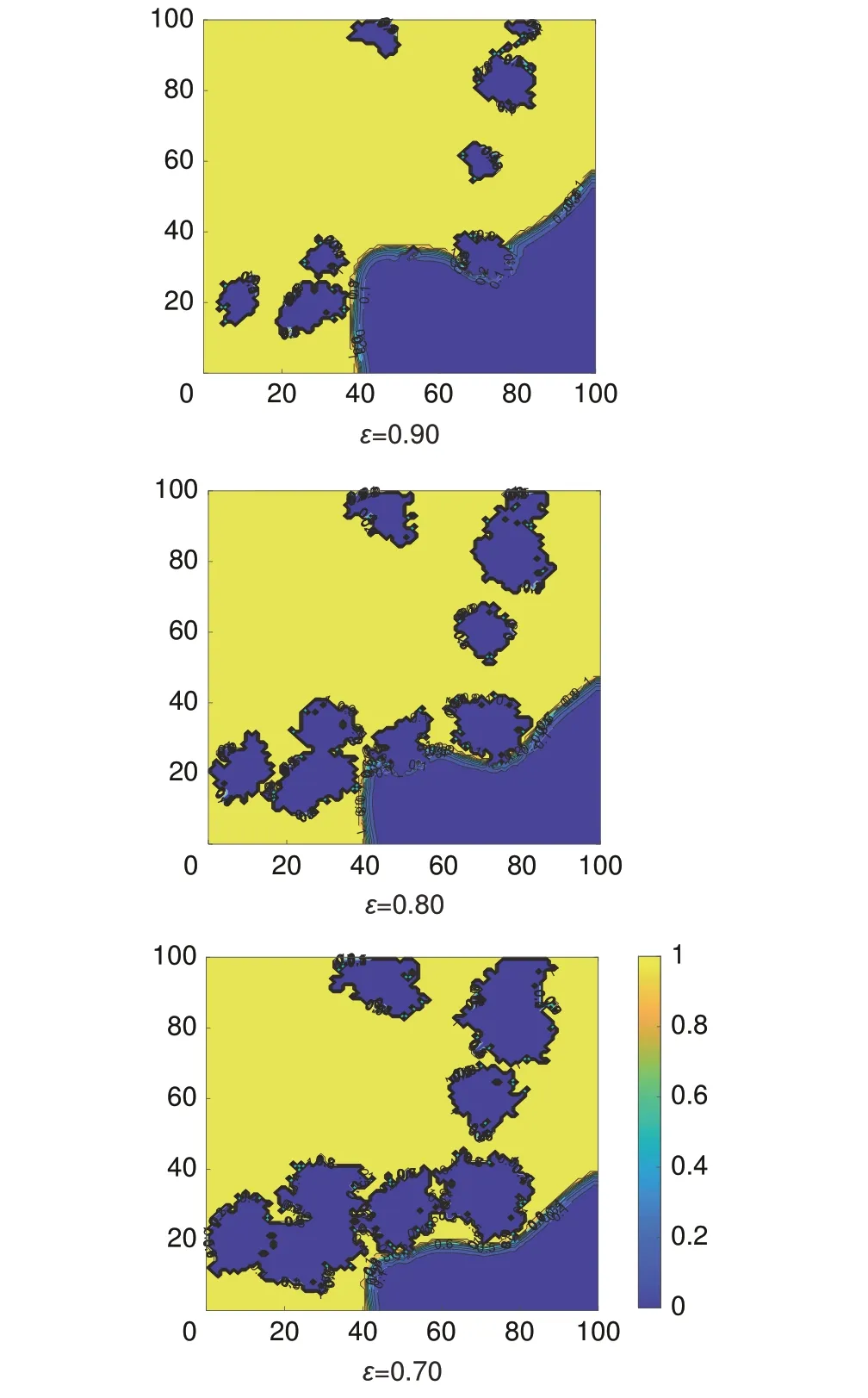
图4 不同ε下的CPCM液相分布云图(Fo=0.72)Fig. 4 Cloud image of CPCM liquid phase distribution under different ε(Fo=0.72)
图5 展示了不同ε下CPCM 的平均温度、液相体积分数与Fo的关系,对比图5(a)中的温度曲线可以看出,当Fo<0.24时,不同ε下的CPCM温度差别不大,这主要是因为,此时左壁面处PCM 刚接触到第一个骨架左侧边缘,骨架参与导热的部分极少,因此对CPCM 温度影响不大。当Fo>0.24 时,不同ε的CPCM 温度变化差别较大,ε=0.70与ε=0.95的CPCM温度提升比与Fo的关系见表2,由表2 可知,当Fo为0.72 时,ε=0.70 与ε=0.95 的CPCM 温度提升比突然增大,这是因为ε=0.70比ε=0.95的CPCM遇到的骨架含量突然增多,热量更快地通过骨架传递到PCM,使得骨架右侧PCM 达到熔化温度,此时主要受随机多孔骨架位置的影响。同时随着ε减小,CPCM 温度上升较快,当Fo=1.20、ε=0.70 时CPCM 的平均温度为0.896,相比ε=0.75、0.80、0.85、0.90、0.95 分别增加了1.82%、4.31%、7.95%、12.28%、14.16%。图5(b)展示了不同ε下液相体积分数随Fo的变化规律,可见随Fo增大,不同ε下的PCM 逐步发生相变,当Fo=0.60 时,ε=0.70 的CPCM 液相体积分数比ε=0.75、0.80、0.85、0.90、0.95分别增加了3.68%、7.20%、11.13%、15.01%、19%,这意味着多孔介质骨架含量对液相体积分数影响较大。当Fo=1.08 时,ε=0.70 的CPCM 首先达到完全熔化阶段,同时还可以发现ε越小,CPCM熔化时间越短,ε=0.70 的CPCM 完全熔化所需的时间比ε=0.80、0.90 缩短了13.59%、23.63%。基于以上分析得出结论,ε对CPCM的平均温度和液相体积分数均影响明显,ε越小,熔化速度越快,CPCM 储热效率越高,同时骨架分布密度对相变过程也有一定影响。
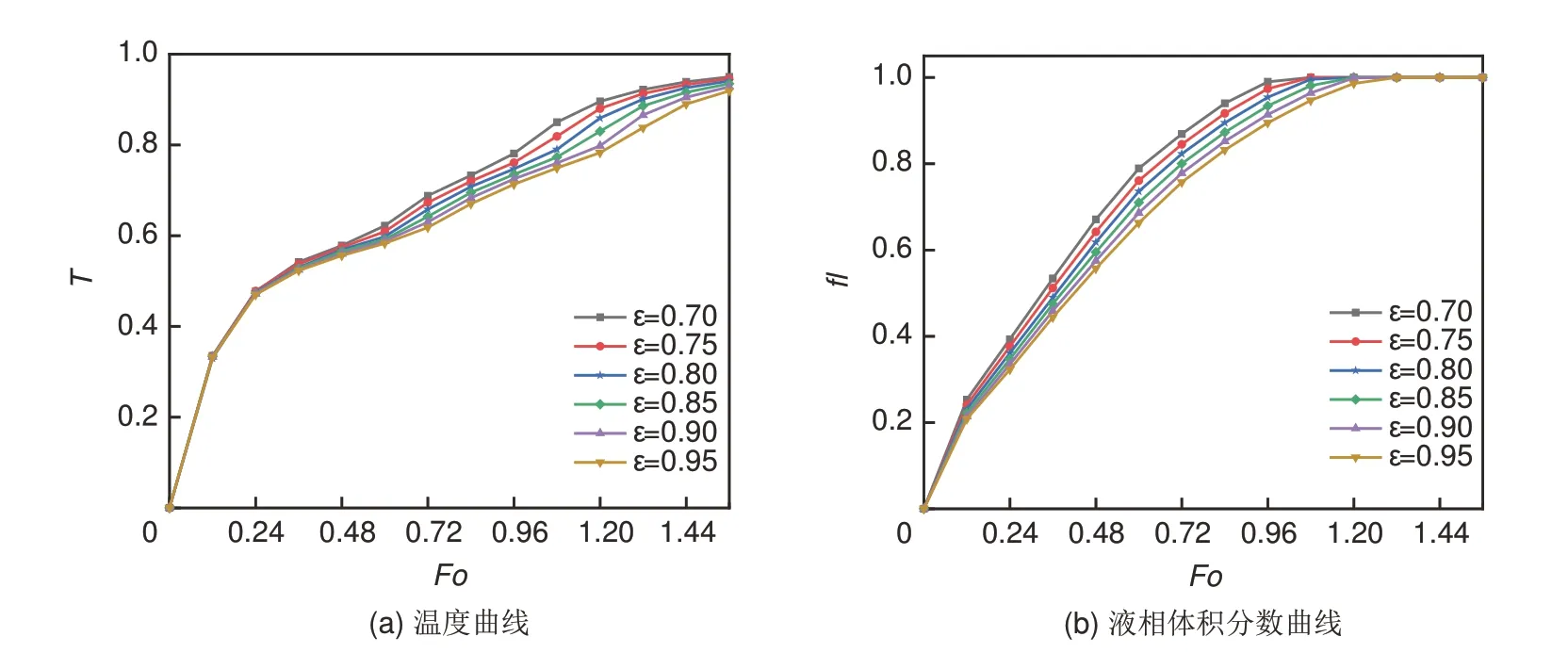
图5 不同ε下CPCM的平均温度、液相体积分数与Fo的关系Fig. 5 Relationship between CPCM average temperature, liquid fraction, and Fo under different ε

表2 ε=0.70与ε=0.95的CPCM平均温度提升比与Fo的关系Table 2 Relationship between average temperature rise ratio of CPCM with ε=0.70 and ε=0.95 and Fo
2.2 骨架形貌Pc及Pd的影响
Pc表示区域内网格节点成为生长核的概率,对随机骨架结构的影响较为显著,Pd表示生长核在周围8个方向上的生长概率,对重建结构的骨架形态影响较小。为了研究Pc、Pd对相变过程的影响,在ε为0.90 的前提下,分别建立3 种不同Pc(0.0001、0.001 和0.01)和3 种 不 同Pd(0.0001、0.001 和0.01)的相变模型。图6展示了Fo=0.96时,不同Pc下的CPCM液相分布云图。从图6中可以看出,Pc越大,重建结构中多孔骨架越微小,分布越均匀,CPCM 液相体积分数增大,Pc=0.01 的液相体积分数相比Pc=0.0001、0.001提高了0.32%、1.36%。

图6 不同Pc下的CPCM液相分布云图(Fo=0.96)Fig. 6 Cloud image of CPCM liquid phase distribution under different Pc (Fo=0.96)
图7分别展示了不同Pc、Pd下的CPCM液相体积分数与Fo的关系,对比图7(a)中的液相体积分数可以看出,3种不同Pc下的CPCM液相体积分数随着Fo的增大而提高,当Fo=1.20时,Pc=0.01最先达到完全熔化阶段,相比Pc=0.001、Pc=0.0001时间缩短了16.03%、19.43%。从图7(b)中的液相体积分数曲线可以看出,Pd=0.0001 的CPCM 的液相体积分数最大,当Fo=0.48 时,Pd=0.0001的液相体积分数为0.5816,相比Pd=0.001、0.01提高了1.13%、3.54%。基于以上分析得出结论,Pc越大,骨架分布越均匀,周围PCM增多,熔化时间缩短,熔化速度加快。Pd越小,熔化速度较快。

图7 液相体积分数与Fo的关系Fig. 7 Relationship between volume fraction of liquid phase and Fo
将图5(b)与图7(a)、(b)进行对比分析可得,Pc、Pd相对于ε对相变储能特性的影响较小,这是因为当ε(0.90)一定时,骨架的分布密度与形貌对相变储能的影响相对较小。
2.3 Ra的影响
为了研究Ra对相变储能的影响,在ε为0.90的前提下,建立了Ra分别为103、104、1.8×104的二维方腔相变模型进行模拟。图8 展示了Fo=0.84 时,Ra为1000、10000、18000 的CPCM 温度分布云图。从图8中可以看出,3种Ra下的等温线均发生弯曲,这是因为自然对流产生的浮升力加速了方腔上部流动与传热强度,使方腔上部PCM的熔化速率大于方腔下部,从而发生弯曲。同时随着Ra增大,方腔内的自然对流作用越强,等温线弯曲程度越大。当Ra=1000 时,靠近左壁面PCM的等温线弯曲较小,意味着此时相变过程的传热方式以导热为主,自然对流的影响很小;当Ra=18000时,等温线弯曲程度很大,意味着此时相变过程的传热方式以自然对流为主。
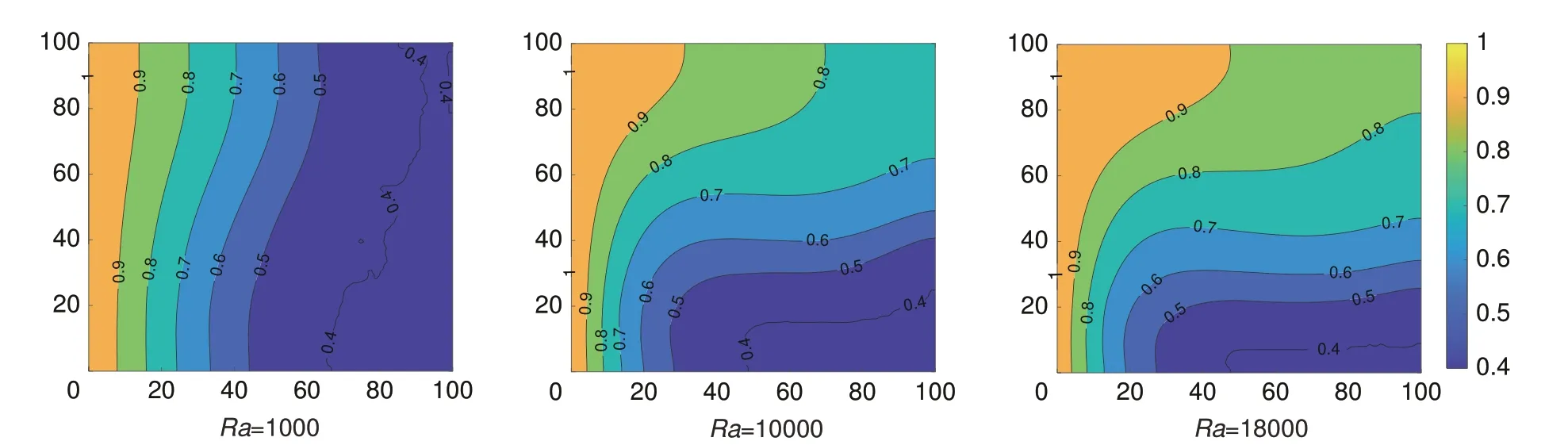
图8 Fo=0.84时不同Ra的温度分布云图(Fo=0.84)Fig. 8 Cloud diagram of temperature distribution of different Ra at Fo=0.84
图9展示了不同Ra下CPCM的平均温度、液相体积分数与Fo的关系,从图9(a)中可以发现,随着Fo增大,Ra=18000的CPCM平均温度越大,当Fo=1.20 时,Ra=18000 的CPCM 温度为0.8801,相比Ra=1000、10000分别提高了27.1%、9.33%。从图9(b)中可以发现,当Fo=0.96时,3种Ra液相体积分数相差最大,此时Ra=18000 的液相体积分数为0.9682,相 比Ra=1000、10000 增 大 了25.57%、5.6%。当Fo=1.08时,Ra=18000的CPCM首先完全熔化,同时Ra=18000所需熔化时间最短,相比Ra=1000、10000减少了41.46%、22.74%。基于以上分析得出结论,Ra越大,自然对流越强,CPCM熔化速度越快,温度上升越快,所需熔化时间越短。

图9 不同Ra下CPCM的平均温度、液相体积分数与Fo的关系Fig. 9 Relationship between CPCM average temperature, liquid volume fraction, and Fo under different Ra
3 结 论
本工作基于焓的LBM 对随机多孔介质无机CPCM储能特性进行研究,探究ε、Pc、Pd、Ra对无机CPCM相变过程的影响,研究结论如下:ε越小,骨架含量越大,CPCM 融化时间越短。ε为0.70 的PCM 完全熔化时间相较于ε为0.90 缩短了23.63%。在 相 同ε(0.90)下,Pc越 大 或Pd越 小,CPCM 熔化速度越快。Ra越大,自然对流强度越大,CPCM 所需熔化时间越短。Ra=18000 所需熔化时间比Ra=1000减少了41.46%。

