2.5D编织复合材料齿轮性能仿真分析

刘舒伟，王旭鹏，，刘峰峰，唐欣尧，张卫亮，薛藤元

(1.西安理工大学 军民融合防护装备设计创新研究中心， 西安 710054； 2.西安理工大学 机械与精密仪器工程学院， 西安 710048)

0 引言

从20世纪60年代开始，众多学者开始了对三维编织复合材料这一新型材料的研究[1]。2.5D作为三维编织复合材料的一种，同样大受关注。在齿轮方面，齿轮的弯曲、接触等性能的研究一直是力学分析的基本要素。国内外众多学者对其力学性能分析展开了广泛且深入的研究。

对于材料方面，杨甜甜[2]对2.5D机织复合材料的细观结构、拉伸弯曲力学性能等进行了试验及有限元研究。李居影等[3]建立了2.5D复合材料单胞模型，仿真分析了材料沿经向拉伸下的弹性性能，并与试验进行了对比分析。而在齿轮方面，王羽达等[4]研究了一对直齿圆柱齿轮啮合时的接触应力和传动误差等的变化。陈龙等[5]构建了能够用于IGA分析的多片拼接NURBS曲面参数化模型。范乃则等[6]采用有限元软件Abaqus计算了城轨列车传动系统不同工况下的应力变化，为齿轮箱的开发应用提供了参考。Ignacio等[7]基于网格细化的多点约束的应用提出了一种能够以低成本获得接触应力和弯曲应力精确结果的有限元模型。裴未迟等[8]基于Abaqus计算了半椭圆形裂纹前缘应力强度因子，并分析强度因子的影响规律。Chavadaki等[9]采用2种合金材料对齿轮弯曲应力和变形进行了详细的分析。Mohsenzadeh等[10]分析了纯聚甲醛和聚甲醛/炭黑纳米材料齿轮的啮合过程。王雁东等[11]针对航空齿轮提出了一种轻量化设计方案。余国达等[12]建立了塑料齿轮啮合温度场有限元数值模型，预测了塑料齿轮的啮合温度，并与实验结果进行对比。赵中轩等[13]分析了弹性体高分子复合材料齿轮的啮合特性，并设计了一种高分子复合材料齿轮磨损量的测量系统。Cerne等[14]制备了碳纤维复合材料与金属齿轮，对其分别采用试验及有限元分析，研究了复合材料齿轮的力学性能，并提出了一种提高齿轮力学性能的方法。Lu等[15]制作了聚合物齿轮，建立了相应的疲劳模型，预估了聚合物齿轮的接触疲劳寿命，并进行了相关疲劳寿命试验，验证了有限元的正确性。Lu等[16]建立了具有lunker缺陷的聚合物齿轮疲劳模型，并进行了耐久性试验。学者们对于齿轮的研究大都集中在它的力学性能上，齿轮本身的材料的研究并不是很多，对于复合材料在齿轮上的应用的研究也较少，因此，针对未来陆上机动平台对轻量化、高效化传动装置的需求，实现碳纤维复合材料齿轮与金属齿轮同等承载下的减重需求，进行2.5D编织复合材料齿轮的力学性能分析。

基于2.5D编织复合材料的结构特点，将纱线截面假设为八边形，建立起便于力学性能分析的单胞模型，在单胞模型的基础上进行其刚度力学性能分析，将2.5D编织复合材料应用到机械齿轮上，基于有限元分析软件Abaqus对齿轮啮合进行静应力分析，以实现齿轮的优化设计。

1 单胞几何模型

三维编织复合材料可以分为三维多向编织复合材料、三维正交编织复合材料和三维角联锁织物复合材料(2.5D编织复合材料)。2.5D编织复合材料主要是采用机织和编织或者半机织半编织的方法成型，经向纱和纬向纱相互缠绕互锁同时厚度方向的纱线以某一确定的角度与经向纱和纬向纱交织起来[17]，这就使2.5D编织复合材料具有良好的层间力学性能、抗剪切性、结构整体性和可设计性。

1.1 材料模型

2.5D编织复合材料按经纱交织深度可分为浅交联和深交联。深交联结构经纱贯穿整个构件厚度，织物变形量大，浅交联结构经纱并不贯穿整个结构厚度，结构的表面损伤并不会使整个结构厚度的经纱都断裂，较好地保持了结构的完整性[18]。浅交联结构最常见的形式为浅交弯联和浅交直联结构。根据纱线的走向和屈曲状态可将纱线分为两类：经纱和纬纱，其中部分复合材料根据实际需要沿经纱方向增加了平直的增强纱系。

选定2.5D经向增强浅交弯联结构为研究对象，如图1，黑点代表的为纬向纱，绕过纬向纱的为经向纱，虚线代表的为经向增强纱，以此种结构建立其材料实体模型[19]。采用三维实体建模软件Creo实现单胞模型的参数化建模。根据参考公式得到单胞几何模型，如图2所示。

图1 经向增强浅交弯联结构示意图

图2 2.5D纱线实体模型示意图

1.2 纤维束弹性性能

2.5D编织复合材料是由纤维束和树脂基体复合而成，纤维束在轴向方向力学性能最强，其他2个方向力学性能相近，故纤维束可被视为横观各向同性材料。基体则各个方向力学性能相近，为各向同性材料。现有文献一般采用如下公式计算纤维束的等效弹性模量[20]。

E11=vsEf1+(1-vs)Em

u12=u13=vsuf12+ (1-vs)um

(1)

式中：E11为纤维束轴向弹性模量；E22和E33为纤维束横向弹性模量；G23为纤维束横向剪切模量；G12和G13为纤维束轴向剪切模量；u23为纤维束横向泊松比；u12和u13为纤维束轴向泊松比；Ef1为纤维轴向弹性模量；Ef2为纤维横向弹性模量；uf12为纤维轴向泊松比；Gf12为纤维轴向剪切模量;Gf23为纤维束横向剪切模量；Em为基体弹性模量；um为基体泊松比；vs为纤维束中的纤维体积含量。

式(1)中组分材料的参数见表1。

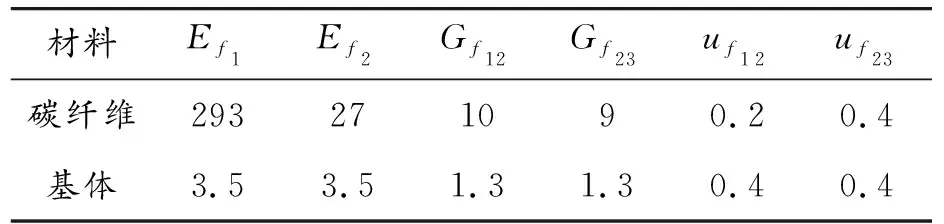
表1 组分材料的弹性性能参数 GPa

纤维体积分数(纱线填充因子)为0.8，计算得到纤维束的弹性性能参数如表2。

表2 纤维束的弹性性能参数 GPa

1.3 单胞模型

2.5D经向增强浅交弯联结构具有周期性。为了节约计算成本，采用单胞模型作为研究对象计算材料的整体力学性能。单胞模型能够通过平移变换得到材料整体结构，单胞分为内部单胞、表面单胞和棱角单胞，而表面和棱角单胞所占比例较小，故本文只研究其内部单胞，其内部单胞模型如图3所示。

图3 内部单胞实体模型示意图

2 材料有限元分析

将通过计算得到的纤维束的弹性力学性能在Abaqus中对单胞进行有限元分析，从而得到材料整体的弹性性能。

2.1 网格划分

首先将通过Creo建好的单胞实体模型转换成中性Stp格式，导入网格划分软件Hypermesh中，对纤维束和基体分别单独划分网格。由于后期要对其施加周期性边界条件，故在划分网格时需划分周期性网格，相对面的网格节点数目要保持一致，并使相对面的节点一一对应以保持力传递的连续性。采用四面体网格划分方法，单元类型为C3D4R，单胞网格模型如图4所示，单胞模型结点总数为40 531，单元总数为216 939。

图4 单胞网格划分模型示意图

2.2 周期性边界条件

单胞模型可以大大减少有限元计算的时间及成本，但单胞模型的力学性能与原材料有一定的差距，所以合理施加边界条件是获得准确力学响应的前提。由于施加周期性边界条件比较复杂，故通过python程序施加多点约束方程，进而施加周期性边界条件，如图5所示，分析步采用静力通用分析步。

图5 单胞周期性边界条件示意图图

2.3 有限元结果

图6为单胞模型施加单向拉伸和剪切载荷后材料应力云图，施加在单胞表面上的位移在内部受到抵抗，在位移的边界表面上产生边界节点应力，通过输出边界节点的应力，用平均应力除以平均应变即可得到这个方向上的弹性模量。

图6 单胞受力应力云图

(3)

为了计算材料3个方向的弹性性能，需要分别对3个方向施加拉伸应力和剪切应力来求解单胞的弹性常数。

基于Abaqus的有限元分析得到材料单胞的各个方向的弹性性能参数，如表3所示。

表3 单胞弹性性能参数 GPa

3 齿轮有限元分析

3.1 模型分析

图7表示为一对外齿直齿轮啮合情况，其重合度大于1，N1、N2为两齿轮基圆公切线的切点，N1N2为理论啮合线。O2为主动轮圆心，O1为从动轮圆心，A、B为主动轮齿顶与从动轮啮合的起点位置，齿轮啮合过程中AD、CB段为双齿啮合区，DC段为单齿啮合区。齿轮传动过程中齿轮的法向载荷不断变化。故齿轮在啮合过程中齿面上产生的接触压力也随着运转不断变化，由赫兹应力接触公式可知：

图7 齿轮啮合示意图

(2)

式中：σH为齿轮所受接触应力(MPa);E1,E2为齿轮1、2材料的弹性模量(MPa)；u1,u2为齿轮1、2的泊松比；L为接触面长度(mm)；R1、R2为齿轮1、2的分度圆半径(mm)；Fn为齿轮所受扭矩(N·m)。

由赫兹公式可知，齿轮所受接触应力与扭矩呈非线性关系。这是由于扭矩的增大，齿轮由于弹性形变，所受力接触面积增大，相应接触应力变小。

3.2 齿轮模型

确定齿轮参数，根据实际齿轮参数在Solidworks中生成一对啮合齿轮，如图8所示，齿轮参数如表4所示。

图8 齿轮啮合模型示意图

表4 齿轮参数

3.3 网格划分

由于计算接触应力所需网格密度较大，为了减少计算成本，只选取6个齿计算啮合过程中齿轮所受接触应力(图9)。将Solidworks中生成的齿轮导入网格划分软件Hypermesh中划分六面体网格(C3D8R)，单个网格越小，网格越密，计算所得的网格精度越高，但随之计算时间更长，计算效率更低，故要适当划分网格密度，本文中网格划分齿轮的节点数为579 474个，单元数为618 249。然后将划分好的网格导入有限元分析软件Abaqus中进行齿轮啮合性能分析。将计算得到的2.5D编织复合材料的弹性常数附加到齿轮的工程常数中，从而计算齿轮的受力情况。

图9 齿轮的啮合过程示意图

3.4 载荷及边界条件

在Abaqus中计算动态齿轮啮合时采用全柔性体的仿真分析方法进行。在齿轮啮合可能接触的面上设置接触对，接触类型为“面-面”接触，同时2个齿轮都只给绕Z轴方向的转动自由度。动态过程中分为2个分析步，分析步类型都采用静力通用分析步，第1个分析步中给右齿轮施加顺时针方向100 N·m的力矩，左齿轮保持不动，模拟齿轮在运动前即将运动的临界过程，在第2个分析步中给左齿轮中心施加顺时针转动位移，计算齿轮啮合过程的应力变化。

3.5 有限元结果

3.5.1弯曲应力分析结果

当施加100 N·m的力矩时，主动轮和从动轮所受弯曲应力分布如图10所示。通过分析可以得到齿轮在齿根所受最大弯曲应力为98.59 MPa。

图10 最大弯曲应力云图

分别计算了50～300 N·m间6个不同扭矩下齿轮所受弯曲应力的大小，并绘制出齿轮的弯曲应力随扭矩变化曲线，如图11。在许用载荷范围内，齿轮的最大弯曲应力与扭矩呈线性变化关系。

图11 弯曲应力-扭矩关系曲线

3.5.2接触应力分析结果

齿轮在运动过程中，相应齿轮不断相互接触啮合。在直齿圆柱齿轮啮合过程中，齿面沿轴线方向的节点受力情况基本相同，故而将三维齿轮简化为二维来分析其受力情况。以从动轮上的一个齿轮作为研究对象，如图12(a)所示。选取单侧从齿顶A到齿根D处的19个节点作为研究对象，分析在啮合过程中不同节点所受应力变化。

图12 单侧节点选取示意图

齿轮的齿廓可以分为双齿啮合区和单齿啮合区，以从动轮的一个齿为参考，齿根和齿顶附近的区域为双齿啮合区域，中间区域为单齿啮合区域，如图12(b)所示。在力学分析中，单齿接触面上的接触应力大于双齿齿面上的接触应力，所以中间的单齿啮合区域被认为是最容易损坏的区域。但是双齿啮合区域由于突然的冲击，其所受载荷非常高，甚至可能大于单齿啮合区域的载荷，因此，齿根和齿顶附近的区域也很容易受到损伤，需加以考虑。

图13为当施加100 N·m的力矩时，齿轮单面从啮入到啮出齿轮所受应力云图，齿轮从D点开始啮入，B点其所受应力达到最大值，然后从A点啮出，形成一个完整的单齿齿面啮合过程。

图13 单齿啮入啮出应力云图

图14为一个齿面上各个节点在啮合过程中所受接触应力的变化情况。由图14可知，该齿面节点在1.2 s齿根开始啮合，在1.7 s时齿顶结束啮合。齿轮的最大接触应力为222.7 MPa，为节点2 171 006所受应力，可知当齿轮啮合程度达到最大时齿轮所受接触应力最大。

图14 单齿啮合接触应力变化曲线

图15为主动轮在一个弧度过程中最大接触应力随时间的变化曲线。由图15可知，当齿轮平稳运行时，齿轮的最大接触应力呈现周期性变化，变化的一个周期约为0.27 s。在周期性变化的同时其最大接触应力基本保持不变。

图15 主动轮最大接触应力随时间的变化曲线

同样，分别计算了50～600 N·m间不同扭矩下齿轮所受接触应力的大小，并绘制出齿轮的最大接触应力随扭矩变化曲线，如图16所示。在许用载荷下，齿轮的最大接触应力与扭矩呈非线性变化关系。

图16 最大接触应力-扭矩变化曲线

4 结论

将2.5D编织复合材料应用到齿轮啮合的静力学分析过程中，分析了不同扭矩下复合材料齿轮的接触应力和弯曲应力的变化规律：

1) 在许用载荷下，齿轮的最大弯曲应力与扭矩呈现线性变化规律；

2)在许用载荷下，齿轮的最大接触应力与扭矩呈非线性变化关系。

本研究为2.5D编织复合材料性能分析及其在齿轮传动系统领域的应用提供了参考。后续将对2.5D编织复合材料齿轮的编织方式和实现进一步研究与探索。