区间图最小连通支配集问题的最优算法

周星宏，李 鹏，王爱法，赵文平

(重庆理工大学 理学院， 重庆 400054)

0 引言

图的支配集理论近年来已成为图论中发展较快的分支之一，在社会网络[1]、自适应网络[2]、统计力学[3]、编码理论[4]、监控系统[5]等领域被广泛应用。支配集中存在许多变形问题，如双重支配集、罗马支配集、连通支配集、最小支配集、永恒支配集等。其中连通支配集因其在无线传感器网络中的重要作用受到学者的广泛研究，详见文献[6-10]。受传统有线网络物理骨干网的启发，学者们提出将虚拟骨干网引入到无线传感器网络的拓扑控制中，以减少网络资源的消耗。因此，将无线传感器网络构造为磁盘图时，虚拟骨干网即是图的连通支配集，并需同时具备以下2个属性：①每个不在虚拟骨干网中的节点可直接与相邻的节点通信；②虚拟骨干网中的所有节点都能在虚拟骨干网内相互通信。为使虚拟骨干网尽可能小，学者们继续研究最小连通支配集(MCDS)。而区间图MCDS问题是该方向的重要课题。

区间图是弦图的一个子类，在信息存储分配和特殊的网络管理等领域有着重要应用，与其相关的支配集问题近年来有如下研究：Braga等[11]证明了对于单位区间图中的永恒支配集问题可在线性时间内解决；Soulignac[12]通过改进算法，提出时间复杂度为O(|E(G)|)的算法来求解单位区间图上的双重支配集问题；Araki等[13]提出可在O(|V(G)|)时间内求出连通单位区间图在给定连续排序下的最小安全支配集；对于区间图的最小支配集问题，Das等[14]提出了一种新的求解支配集的算法，该算法求解的支配集在一定的条件下是最优的；Rinemberg等[15]证明了区间图的永恒支配数和团连通覆盖数是一致的；Lin等[16]证实了区间图的外连通支配集问题可在O(|V(G)|)时间内求解。

将对实线上n个区间的MCDS问题进行研究，分为以下4个部分：首先，介绍相关的基础知识；其次，回顾区间图连通支配集问题求解的相关算法并指出其不适用之处，进而提出求解区间图MCDS的线性算法且进行了理论分析和实例验证；再次，给出该算法的时间和空间复杂度分析；最后，对文章进行总结并提出下一步的研究计划。

1 基本概念

所用的图都是简单图，即有限、无向、无自环、无重边的图。不失一般性，假设每个区间都包含2个端点，且没有2个区间共用一个公共端点。

定义1当u和v是一条边的2个端点时，它们是邻接的且互为邻居。

定义2v在图G中的邻居集合加上v本身称为v的闭邻域，记为NG[v]。

定义3顶点v的度(在无自环图中)是关联边的数目，记为degG(v)。

定义4给定简单无向图G=(V，E)和集合D⊆V，如果V中的每个顶点都属于D或与D中的至少一个顶点相邻，则D称为G的支配集。

定义5支配数γ(G)是G中支配集包含顶点数的最小值。

定义6集合Dc是图G的顶点集V的子集，即Dc⊆V(G)，如果集合Dc是图G的一个支配集，且其导出子图G[D]是连通的，那么称Dc是G的一个连通支配集。

定义7连通支配数γc(G)是G中连通支配集包含顶点数的最小值。

定义8图G为区间图，如果图中每个顶点v与直线上的某个闭区间集I之间一一对应，且2个顶点邻接当且仅当它们对应的区间有非空的交。

定义9若G是区间图，且G存在一个区间表示，使得每个顶点对应的区间长度都一致，则称G为单位区间图。

2 相关算法

由于无线传感器网络中，既没有任何固定的基础设施，也没有任何集中的控制，且随着节点数量的增加，网络性能会受到影响。因此，为了实现高效的路由，可以选择其中一些节点组成一个虚拟骨干网，从相关网络的节点构造一个称为区间图的图模型。2012年，Sudhakaraiah等[17]提出了区间图的连通网络支配集算法，经研究发现Sudhakaraiah等的算法是不适用的，2.1小节中给出了该算法的详细过程，并对其不足之处进行说明。2.2小节中提出了区间图上求解MCDS的最优多项式算法。

2.1 算法回顾

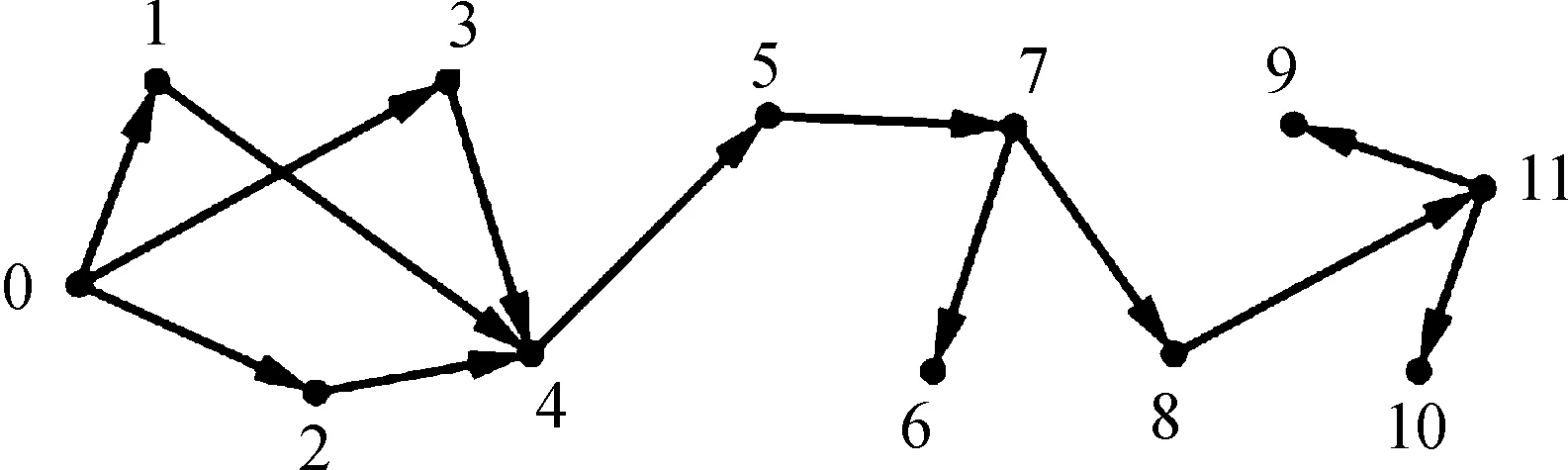
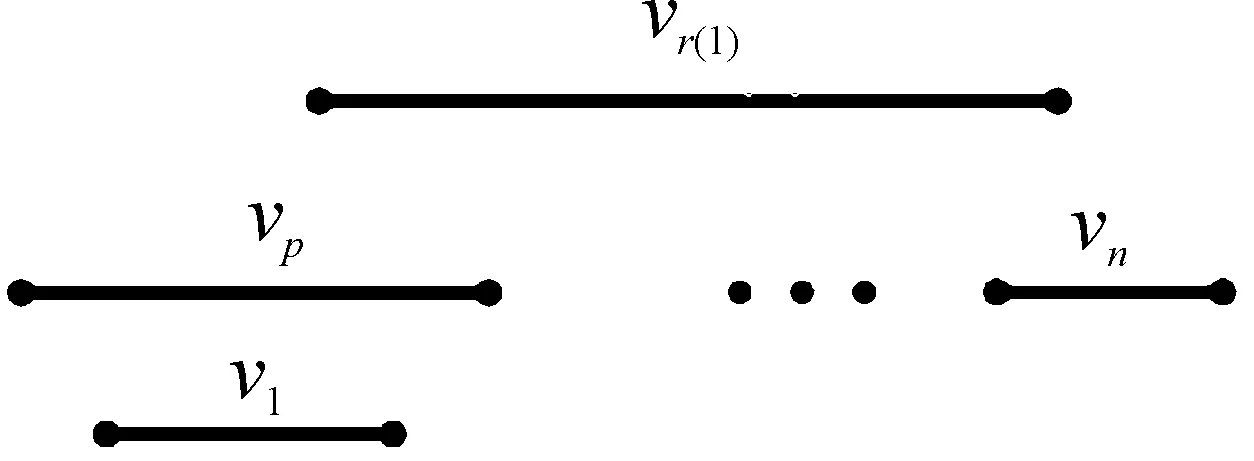
算法1中的符号变量说明：2个区间i=[ai,bi]，j=[aj,bj]，非相交区间NI(i)=j，如果bi

算法1区间图的MCDS算法[17]

Input：interval familyI={1,2,3,…,n}

Output：minimal connected network dominating set of an interval graph from a directed networkD

Step1: fori=1 ton

{p=NI(i)

q=min(i)

R=nbd[p]

S=nbd[q]

Next(i)=min({R}{S})

ifNext(i)=nullthen go to Step1

else

joinitoNext(i) and go to Step1}

Step2: forj=2 ton

{ ifI1is intersect toIjcontained inIj

joinI0toIj,

ifIn+1is intersect toIjcontained inIj

joinIn+1toIj}

Step3: find pathsP1,P2,…,Pkfor somekfrom

node forI0toIn+1

Step4: forj=1 tok

{ if nodes ofPjare connected inG,

MCDS={nodes ofPj} }

Step5: end

例1用算法1求下面区间图G的MCDS。图1和图2均来自参考文献[17]，但顶点2、3的顺序未按右端点排序。

图1 区间图G(例1)

步骤1

nbd[1]={1,2,3}，nbd[2]={1,2,3,4}

nbd[3]={1,2,3,4}，nbd[4]={2,3,4,5,6}

nbd[5]={4,5,6,7}，nbd[6]={4,5,6,7,9}

nbd[7]={5,6,7,8,9}，nbd[8]={7,8,9,10}

nbd[9]={6,7,8,9,10}，nbd[10]={8,9,10}

min(1)=1，min(2)=1，min(3)=1

min(4)=2，min(5)=4，min(6)=4

min(7)=5，min(8)=7，min(9)=6

min(10)=8

NI(1)=4，NI(2)=5，NI(3)=5

NI(4)=7，NI(5)=8，NI(6)=8

NI(7)=10，NI(8)=null，NI(9)=null

NI(10)=null

Next(i)= min({nbd[N(i)]} {nbd[min(i)]})

Next(1)= min({nbd[N(1)]} {nbd[min(1)]})

= min({nbd[4]} {nbd[1]})

= min({2,3,4,5,6} {1,2,3})=4

Next(2)=min({nbd[N(2)]} {nbd[min(2)]})=4

Next(3)=min({nbd[N(3)]} {nbd[min(3)]})=4

Next(4)=min({nbd[N(4)]} {nbd[min(4)]})=5

Next(5)=min({nbd[N(5)]} {nbd[min(5)]})=7

Next(6)=min({nbd[N(6)]} {nbd[min(6)]})=7

Next(7)=min({nbd[N(7)]} {nbd[min(7)]})=8

Next(8)=min({nbd[N(8)]} {nbd[min(8)]})=null

Next(9)=min({nbd[N(9)]} {nbd[min(9)]})=null

Next(10)=min({nbd[N(10)]} {nbd[min(10)]})=null

步骤2如图2所示，把区间图扩大，在首尾扩展2个虚拟区间I0和In+1，然后得到一个定向网络图[17]，如图3所示。其中N={0,1,2,3,4,5,6,7,8,9,10,11}，L=L1∪L2。

图2 区间图G首尾扩展2个虚拟区间I0和In+1

图3 定向网络图D(N，L)

步骤3由图3可以得到3条路径分别为：0-3-4-5-7-8-11；0-2-4-5-7-8-11；0-1-4-5-7-8-11。

步骤4输出结果为{3,4,5,7,8}，{2,4,5,7,8}。

步骤5结束。

但是可以找到D={v2,v4,v6,v9}是区间图G的MCDS。明显地，对于图1的MCDSγc(G)=4≠5，所以，算法1输出的结果不是MCDS，因此Sudhakaraiah等的算法是不适用的。

2.2 区间图MCDS问题的线性算法

以下是提出的区间图MCDS算法。算法中输入的区间图都是连通的。

算法2区间图MCDS问题算法

Input：一个区间图G=(V，E)，顶点集V(G)={v1,v2,…,vn}，每个顶点分别对应区间{I1,I2,…,In}，对于1≤i≤n，有Ii=[ai,bi]，其中ai、bi分别是区间Ii的左右端点。其中b1

Output：G的一个MCDSD

Step1：letj=r(1) andD={vr(1)}//Ir(1)是I1本身或与I1相交的右端点最大的区间

Step2：do ifvr(j)∉NG[vl]∥Ir(j)是Ij本身或与Ij相交的右端点最大的区间，

{j=r(j)， andD=D∪{vj}}

Step3：outputD

Step4：end

例2用算法2求下面区间图G的MCDS。

由图4可知左端点最大的顶点为vl=v13，NG[v13]={v12,v13,v14,v15}，根据算法2可得如下步骤：

图4 区间图G(例2)

步骤1G={v1,v2,v3,…,v15}，v1的邻居有{v2,v3}，其中右端点最大邻居为vr(1)=v3，此时j=r(1)=3，D={v3}。

步骤2由步骤1得vr(1)=v3，且v3∉NG[v13]，j=r(3)=6，即v3的邻居中右端点最大的点为v6，D={v3,v6}；v6∉NG[v13]，j=r(6)=7，即v6的邻居中右端点最大的点为v7，所以D={v3,v6,v7}；v7∉NG[v13]，j=r(7)=9，即v7的邻居中右端点最大的点为v9，所以D={v3,v6,v7,v9}；v9∉NG[v13]，j=r(9)=12，即v9的邻居中右端点最大的点为v12，故D={v3,v6,v7,v9,v12}；v12∈NG[v13]时，算法结束迭代。

步骤3输出D={v3,v6,v7,v9,v12}。

步骤4结束。

综上γc(G)≤5，经验算知，图4的MCDS为D={v3,v6,v7,v9,v12}，故γc(G)=5。

定理1 算法2输出的集合D是区间图G的一个MCDS。

证明令区间图G=(V，E)，其中V(G)={v1,v2,…,vn}，每个顶点分别对应区间{I1,I2,…,In}，对于1≤i≤n，有Ii=[ai,bi]，其中ai、bi分别是区间Ii的左右端点。其中b1

1) 若γc(G)=1，则|D′|=1，设D′={vp}，因为D′能支配G，所以vp能支配v1，即vp∈NG[v1]，如图5所示。可得p≤r(1)，从而NG[vp]⊆NG[vr(1)]，所以{vr(1)}也是G的MCDS。往证，算法2输出的是D={vr(1)}。设vl是区间图G中左端点最大的点，因为vr(1)可以支配G，所以vr(1)∈NG[vl]。由算法2可知，算法停止迭代，进而输出D={vr(1)}。

图5 γc(G)=1时的区间图

2) 当γc(G)≥2时，由前文的假设可知，D′是区间图G的某个MCDS。所以D′可以支配v1，故存在图G中的某个顶点vk∈D′∩NG[v1]。若vr(1)∉D′，由于vr(1)是v1邻居中右端点最大的点，故NG[vk]⊆NG[vr(1)]，如图6所示。用vr(1)替换vk，即D′-vk+vr(1)也是区间图G的MCDS。因此，不妨设vr(1)∈D′，下面考虑：G*=G-v1-v2-…-vr(1)-1，G*还可表示为G*={vr(1),vr(1)+1,…,vn}。此时vr(1)是图G*在Ir(1),Ir(1)+1,…,In中右端点最小的点，且G*中左端点最大的点仍为vl。由数学归纳原理，通过算法继续迭代，可以得到D*=D-vr(1)是G*的一个MCDS。

图6 γc(G)≥2时的区间图

接下来证明D=D*+vr(1)是区间图G的MCDS，按以下步骤：①D是G的支配集；②D是G的连通支配集；③D是G的MCDS。

首先，D*可支配G*={vr(1),vr(1)+1,…,vn}，且vr(1)能支配{v1,v2,…,vr(1)-1}，故D=D*+vr(1)是G的支配集。

其次，正因为γc(G)≥2，从而vr(r(1))存在。由于D*是G*的一个MCDS，可知vr(1)与vr(r(1))邻接，所以D=D*+vr(1)是连通的，易知，γc(G)≤|D|=1+|D*|=1+γc(G*)。

图7 区间图G的一个

因此|D|=1+|D*|=1+γc(G*)=γc(G)，即D是区间图G的MCDS。

综上，由数学归纳原理知定理1成立。

3 时间复杂度和空间复杂度分析

定理2算法2的时间复杂度和空间复杂度都是线性的。

证明设输入的区间图G=(V，E)，顶点为v1,v2,…,vn，每个顶点对应的区间为I1,I2,…,In。在Step1中，找到j=r(1)(Ir(1)是I1本身或与I1相交的右端点最大的区间)，需要的时间是O(degG(v1))；同理，对于Step2中的每个j，找到r(j)(Ir(j)是Ij本身或与Ij相交的右端点最大的区间)，需要的时间是O(degG(vj))，因此整个算法需要的时间为：

其中：m是G的边数，n是G的顶点数。同时，因为每一步只需存储D，而D的顶点数不会超过n，所以该算法的空间复杂度是O(m+n)。由此可见，整个算法的时间和空间复杂度都是线性的。

4 结论

通过对区间图上MCDS问题的研究，设计线性算法。实例验证和理论分析都表明该算法是线性的，时间和空间复杂度均为O(m+n)。综上，此算法对提高无线传感器网络性能方面具有较高的实际应用价值。下一步，将继续研究图的支配集问题，例如区间图k-罗马支配集问题和安全控制集问题。