交错群图的混合故障诊断问题研究
葛姝媛,原 军
(太原科技大学 应用科学学院, 太原 030024)
0 引言
随着高性能计算的快速发展,多处理器系统的规模也在逐渐扩大。为了保证系统能够稳定运行,必须对系统进行故障诊断。在处理器之间发起测试,利用测试结果来判定故障元素的方法称为系统级诊断,是一种主要的诊断措施。PMC模型是Preparata等[1]在1967年建立的第一个系统级诊断模型。这一诊断模型的特点是,由链路连接的每2个处理器都能分配一个测试,并且处理器的状态影响测试结果的可靠性。在这一开创性的工作之后,BGM模型、比较模型等系统级诊断模型相继被提出。大量围绕着PMC模型、BGM模型、比较模型的研究出现,可参考文献[2-7]。
然而,这些诊断模型假定只发生处理器故障,不发生链路故障。实际当系统投入使用时,处理器和链路可能同时发生故障。因此,为了适应这一混合故障环境,Zhu等[8]在2020年建立了基于PMC模型的系统级诊断模型——HPMC模型。在HPMC模型中,任意2个相邻的处理器和处理器之间的链路可以分配一个测试,这三者分别称为测试者、被测试者和测试边。与PMC模型不同的是,测试结果不仅受到测试者和被测试者状态的影响,与测试边的状态也相关。需特别强调:① 与故障处理器关联的链路总是好的;② 当且仅当测试者无故障,测试结果是可靠的。
与此同时,Zhu等提出了HPMC模型下的h-限制点诊断度和r-限制边诊断度。这2种混合故障诊断度是衡量混合故障环境下系统故障诊断能力的重要参数。随后,文献[8-10]分别确定了超立方体、交换超立方体、类超立方体等无三角正则网络的混合故障诊断度。
交错群图是基于交错群的一类含三角正则网络,因具有点传递性、边传递性、哈密尔顿连通性等良好的性质被广泛研究[11-14]。交错群图是构建多处理器系统的网络拓扑结构之一,其故障诊断度能够反映所构建系统的故障诊断能力,在系统的设计和维护中起重要作用。鉴于此,研究了交错群图在HPMC模型下的2种混合故障诊断度。
1 预备
1.1 符号和术语
设G是由边集E(G)和顶点集V(G)构成的简单无向图。若e=uv∈E(G),则称u和v是相邻的,并称e和u、v是关联的。顶点u的度是指G中与u关联的边的数目,记作d(u)。G的最小度为δ(G)=min{d(u)|u∈V(G)}。如果G中每个顶点的度都等于k,则称G是k正则的。对于任意的顶点u,v∈V(G),cn(u,v)指u和v的公共邻点数。
对于任意的顶点u,NG(u)指G中与u相邻的所有顶点,NEG(u)指G中与u关联的所有边。给定一个顶点集X,G中与X相邻的所有顶点用NG(X)=(∪u∈XNG(u))X表示,且G中与X关联的所有边用NEG(X)=(∪u∈XNEG(u))E(G[X])表示。一般地,在没有混淆的情况下,总是将下标省去。

1.2 交错群图
令p=p1p2…pn是{1,2,…,n}中所有元素的一个排列,即pi∈{1,2,…,n}且当i≠j时,pi≠pj。若当j>i时满足pj n维交错群图AGn[11]是顶点集为V(AGn)=An,边集为E(AGn)={pq|q=pgi,3≤i≤n}的简单无向图。显然,当n≥3时,AGn是2n-4正则的。图1(a)和图1(b)分别为交错群图AG3和AG4。 图1 交错群图AG3和AG4 引理1[12,15]设u和v是n维交错群图AGn中的任意2个顶点。当uv∈E(AGn)时,cn(u,v)=1;当uv∉E(AGn)时,cn(u,v)≤2。 首先给出有关混合故障诊断的一些定义和引理。 定义1[8]设F⊂V和S⊂E分别是多处理器系统G(V,E)的顶点子集和边子集。若任意的uv∈S满足u∉F且v∉F,则称(F,S)为一致故障对。 引理2[8]设(F1,S1)和(F2,S2)是多处理器系统G(V,E)中任意2个相异的一致故障对,则(F1,S1)和(F2,S2)在HPMC模型下是可区分的当且仅当下列条件之一成立: 3) 存在e=uv∈E满足e∈S1S2且u∉F2,v∉F2; 4) 存在e=uv∈E满足e∈S2S1且u∉F1,v∉F1。 定义2[8]设G是一个多处理器系统,t、s是2个正整数。则G在HPMC模型下是(t,s)-可诊断的当且仅当任意2个满足|F1|,|F2|≤t,|S1|,|S2|≤s的相异的故障对(F1,S1)和(F2,S2)是可区分的。 接下来给出h-限制点诊断度和r-限制边诊断度的相关性质。 性质3[8]设G是有m条边且最小度为δ(G)的多处理器系统,且设G在PMC模型下的诊断度为t(G),则 这一节将讨论交错群图AGn(n≥3)在HPMC模型下的h-限制点诊断度和r-限制边诊断度。 情形1F1≠F2。 由F1和F2的对称性,不失一般性,假设|F1F2|≥|F2F1|。接下来,讨论以下3种子情形。 子情形1.1 |F1F2|=1且|F2F1|=1。 图2 不可区分的(F1,S1)和(F2,S2)示意图 子情形1.2|F1F2|=1且|F2F1|=0。 设F1F2={u}。与子情形1.1类似,可得|F2|=2n-h-4。结合|F1F2|=1和|F2F1|=0,可得到|F1|=|F1∩F2|+1=|F2|+1=2n-h-3,与|F1|≤2n-h-4矛盾。 子情形1.3 |F1F2|≥2。 又由于当u和v相邻时cn(u,v)=1,当u和v不相邻时cn(u,v)≤2,故|N({u,v})|=|(N(u)∪N(v)){u,v}|≥d(u)+d(v)-3。结合|S2|≤h可得 (d(u)+d(v)-3)-|S2|≥ [(2n-4)+(2n-4)-3]-h=4n-h-11 (1) 因此 |F1∪F2|≥|NF1∪F2({u,v})|+|{u,v}|≥ (4n-h-11)+2≥4n-2h-8≥ |F1|+|F2| (2) 因此 |F1∪F2|≥|NF1∪F2({u,v,w})|+|{u,v,w}|≥ (6n-18-2h)+3=6n-15-2h 结合|F1∪F2|=|F1|+|F2|=4n-2h-8,可得n≤3,与题设n≥4矛盾。 情形2S1≠S2。 图3 不可区分的(F1,S1)和(F2,S2)示意图 d(u)-|NEF1∪F2(u)|=d(u)-|NF1∪F2(u)|≥ 2n-4-1=2n-5 情形1F1≠F2。 由F1和F2的对称性,不失一般性,假设|F1F2|≥|F2F1|。接下来,讨论以下2种子情形。 子情形1.1|F1F2|=1。 子情形1.2|F1F2|=2。 又由于当u和v相邻时cn(u,v)=1,当u和v不相邻时cn(u,v)≤2,故|N({u,v})|=|(N(u)∪N(v)){u,v}|≥d(u)+d(v)-3。结合|S2|≤2n-7可得 因此 |F1∪F2|≥|NF1∪F2({u,v})|+|{u,v}|≥ (2n-4)+2>2+2≥|F1|+|F2| 与|F1|+|F2|≥|F1∪F2|矛盾。 情形2S1≠S2。 确定了交错群图在HPMC模型下的h-限制点诊断度和r-限制边诊断度,主要结果见表1。结果表明了当任意故障边集的边数不超过最小度时,系统可以识别到的最大故障顶点数,以及当任意故障顶点集的顶点数小于最小度时,系统可以识别到的最大故障边数。这些结果更精确地描述了以交错群图为网络底层拓扑结构的多处理器系统的故障诊断能力,为系统的设计和维护提供了新的参考。 表1 交错群图AGn在HPMC模型下的混合故障诊断度 目前关于混合故障诊断问题的结果较少,如何确定一般含三角网络、非正则网络的h-限制点诊断度和r-限制边诊断度,是下一步要解决的问题。此外,未来可围绕互连网络的混合故障诊断算法进行研究。
2 混合故障诊断理论











3 交错群图AGn的混合故障诊断度





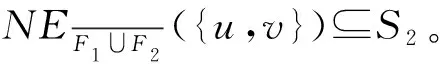

















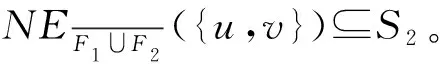



4 结论


