计及多因素聚合储能寿命的微电网容量优化配置

张 莲，赵梦琪，廖宗毅，张尚德，贾 浩，谢文龙，季鸿宇

(1.重庆理工大学 电气与电子工程学院， 重庆 400054; 2.重庆市能源互联网工程技术研究中心， 重庆 400054)

0 引言

当前，扩大新能源的开发利用是解决化石能源问题的必然选择。风能、太阳能的开发技术目前已较为成熟，具有取之不尽的特点，但风光等可再生能源随机性和波动性较大，增加了微电网的配置难度[1]。储能设备能缓解可再生能源出力问题，还能解决用能高峰期的能源消耗问题，达到削峰填谷和改善电网质量的作用[2]。由于储能的造价成本较高，使用寿命相对于其他设备较短，极大制约了微电网的总体经济性，因此如何合理配置风光储的容量显得尤为重要[3]。

目前，国内外专家对风光储容量优化配置进行了大量研究。丁明等[4]以分布式电源的个数作为变量，考虑天气和资源条件对容量配置结果的影响，通过系统运行指标和成本敏感性分析来验证结果的可靠性；窦晓波等[5]提出一种微电网商业运营模式的容量优化配置方法，在满足系统稳定运行和提高系统经济性等方面有较好的效果；胡林静等[6]以场地大小、污染排放量为约束条件，采用多目标免疫粒子群算法进行容量优化配置；为了满足偏远地区的供电需求，高峰等[7]考虑风光出力之间的匹配程度，构建独立的风光储发电系统，以供电可靠性为目标进行优化配置。然而，文献[4-7]都只对风光储的容量进行优化配置，忽略了储能的寿命损耗问题。王磊等[8]考虑了放电次数与放电深度对储能寿命的影响，以储能电站年净收益最大为目标，采用8 760 h生产模拟方法进行求解；文献[9-10]分别提出了固定日循环次数和动态积分的方法对储能寿命损耗问题进行研究；郭明萱等[11]从混合储能的时序互补与储能寿命损耗之间的联系出发，使用固定的充放电策略对储能进行能量管理，验证了充放电策略对储能寿命和容量配置的影响；肖浩等[12]提出了积累损伤的寿命评估方法，量化充放电功率和放电深度对储能寿命的损耗，建立运行规划和寿命评估相结合的双层模型，采用改进粒子群算法计算储能的配置容量。文献[8-12]鲜有考虑放电倍率及温度因素对储能寿命的影响，未对风、光设备进行优化配置。

综上，提出一种考虑多因素聚合储能寿命模型，以投资置换成本量化储能系统的寿命损耗，制定储能控制策略，兼顾投资建设、运行调度以及设备寿命折损等多方面经济性，构建以等年值投资成本和运维成本最小为目标函数的双层优化配置模型，能有效延长储能的使用寿命。最后通过算例仿真分析微电网设备配置结果。

1 储能寿命损耗模型

储能老化表现为使用容量的衰减，一般当使用容量低于额定容量的75%时视为设备报废。研究表明，储能寿命受到温度、放电倍率、放电次数、放电深度等因素的影响。目前普遍用密度函数法、雨流计数法、循环老化和日历老化模型等来计算寿命损耗，但用于规划则过于复杂[13]。

1.1 累积电量寿命模型

累积电量是将每次充放电所对应的储能吞吐量累计起来，当累积电量达到额定吞吐量时，储能设备的使用寿命到达终结。

储能使用后累积的电量为

(1)

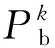
储能积累损耗率为

η=Csum/2NCN×100%

(2)

式中：N为储能循环寿命，CN为储能额定容量。

1.2 多因素聚合寿命模型

1.2.1多因素的影响

1) 温度对寿命的影响

随着温度的变化，储能的老化程度也相应变化。在高温条件下，储能的正负极材料的活性增强，当活性超过上限时，会造成不可逆的损伤，以致影响储能的使用容量；在低温条件下，储能的正负极材料的活性降低，储能的阻抗会升高，导致使用容量下降，从而影响储能的使用寿命[14]。

2) 放电倍率对寿命的影响

放电倍率是指储能在一定时间内释放的容量所对应的电流值，一般额定电流为1C倍率。在不同的倍率下，储能的老化速度不同，随着放电倍率的增加，储能损失容量也不断增大[15]。

3) 放电深度对寿命的影响

放电深度是电池的放电容量和额定容量的比值。随着放电深度的增加，储能的循环次数相应减少，二者呈现反比关系[16]。

1.2.2多因素容量衰退率

储能衰退率为

γsi=Biexp(-a1+a2Ci/RT)(2N·DOD)z

(3)

式中：Ci为不同的放电倍率；Bi、a1、a2及z为不同的放电倍率下所对应的参数；T为热力学温度；R为理想气体常数；DOD为放电深度。

式(3)通常用于固定的循环充放电模式。本文储能运行于不规则放电状态，因此考虑用放电区间内积累吞吐电量来评估储能寿命。

(4)

式中：Ahi为不同的放电倍率条件下的累积吞吐电量，i=1，2，3分别对应不同的放电倍率。

储能实际放电倍率为

(5)

式中：I1c为1倍率下的电流值。

各个大型储能原理上都是由若干小电池串联和并联组合而成，串联和并联会分别增大储能的电压和电流，以此满足大型储能的基本性能。串并联扩容是将大型储能的电量分摊到单体电池上，储能工作由所有单体电池共同完成[17]，因此提出串并联系数，即

lsp=CN1/CN

(6)

式中：CN1为单体电池的额定容量；CN为大型储能的额定容量。

大型储能在运行时，由于无法保证单体电池都工作在同一电压、电流下，造成了储能不均衡现象，因此提出不均衡系数，即

lub=N1/N

(7)

式中：N1为单体电池循环寿命;N为大型储能循环寿命。

考虑多因素的影响，大型储能容量衰退率为

γLi=Biexp(-a1+a2Ci/RT)(lsplubAhi)z

(8)

由储能衰退率可得第i次不规则放电储能损耗成本和使用寿命为：

(9)

Ytime=YγLi/γN

(10)

式中：Ccape设备的总投资成本；Y为运行周期；γN为达到额定使用寿命的衰退率。

2 微电网模型

微网以大电网作为主要能源，风机和光伏为分布式能源。本文中微电网结构由风机(wind turbine，WT)、光伏(photovoltaic，PV)、储能(electrical energy storage，EES)、变换器组成，如图1所示。

1) 风力发电机

风力发电机输出功率与风速有关，其数学模型为

(11)

式中：Pe为时间t内风机额定输出功率，kW；vr、ve、vc分别为切入风速、额定风速、切出风速。

2) 光伏

光伏输出功率受辐照强度、环境温度的影响，其数学模型为

Ppv(t)=PSTCGAC(t){1+k[Tc(t)-Tr]}/GSTC

(12)

式中：PSTC为时间t内光伏的额定输出功率；GAC为时间t内辐照强度；Tc为时间t内太阳能电池板表面温度；Tr为参考温度，取25℃；k为功率温度系数，取值-0.004 7；GSTC为额定辐照强度，取值 1 kW/m2。

3) 电储能

EEES(t)=EEES(t-1)+[Pcha(t)ηcha-Pdis(t)/ηdis]Δt

(13)

式中：EEES(t)为时间t内储能容量；EEES(t-1)为时间t-1内储能容量；Pcha、Pdis和ηcha、ηdis分别为时间t内充放电功率及效率系数；Δt为单位调度时间。

3 微电网容量规划模型

采用双层规划模型，其结构如图2所示，上层为容量规划模型，下层为系统运行模型。

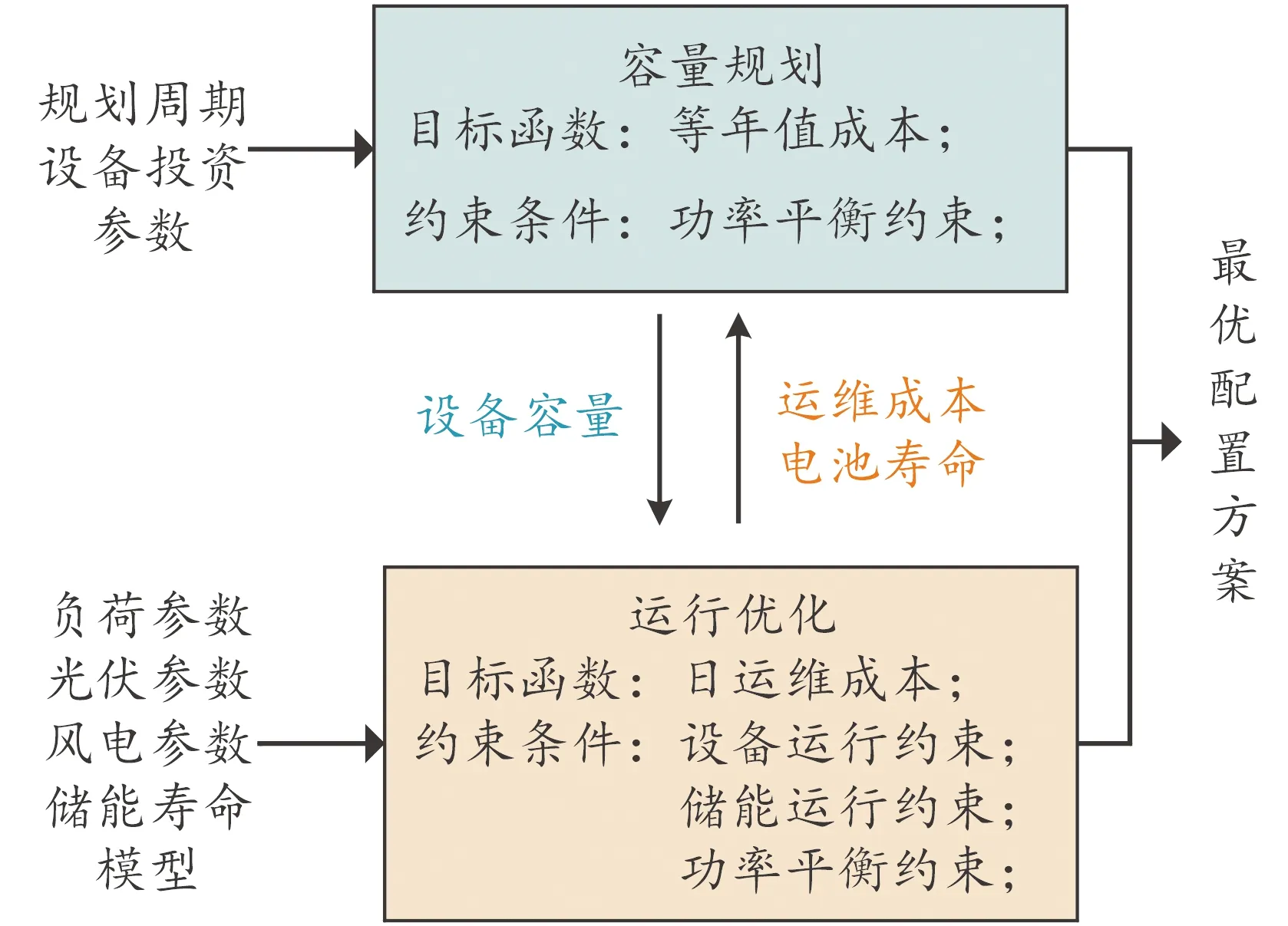
图2 双层规划模型结构示意图

3.1 上层模型

容量规划外层目标为等年值成本最低，可表示为：

minC=(Ccape+Crepe-FRV)rCR+Com+Cline

(14)

设备的建设成本为：

Ccape=Qωcape

(15)

式中：Q为设备的安装容量；ωcape为设备的单位容量成本。

储能的置换成本为：

(16)

储能的设备残值为：

(17)

式中：δFV为储能残值率；γ为贴现率；x=1，2，…，Nrepe+1，代表第x次设备残值回收。

资金回收次数为：

rCR=γ(1+γ)Ya/(1+γ)Ya-1

(18)

设备运行的年维护成本为：

(19)

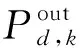
年购电成本为：

(20)

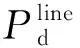
规划周期内储能更换次数为：

Nrepe=Ya/Ytime-1

(21)

式中：Ytime为设备实际使用时间。

受建设场地的限制，电储能投资容量为：

(22)

式中：QESmax为储能安装容量的上限。

3.2 下层模型

容量规划内层目标为日运行成本最低，可表示为：

minc=ces+com+cline

(23)

储能日损耗成本为

(24)

日设备运行维护成本为

(25)

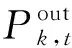
日购电成本为

(26)

3.2.1 功率平衡约束

Pline(t)+Ppv(t)+Pwt(t)=el(t)+Pesbt(t)

(27)

式中：Pline、Ppv、Pwt、el、Pesbt分别为时间t内电网购电功率、光伏消纳的电功率、风机消纳的电功率、电负荷、储能充放电功率。

3.2.2设备运行约束

设备出力约束可表示为：

(28)

rdown≤Pk(t)-Pk(t-1)≤rup

(29)

(30)

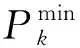
3.2.3储能控制策略

为避免储能设备出现过充和过放现象，对储能单元进行能量控制管理。

储能充放电功率约束为：

(31)

(32)

χcha+χdis=1

(33)

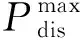
Soc约束为：

Socmin≤Soc(t)≤Socmax

(34)

Soc(t)=(1-μES)Soc(t-1)+

Pcha(t)ηcha/QES-Pdis(t)ηdis/QES

(35)

Soc(t0)=Soc(tN)

(36)

式中：Soc(t)为时间t内储能充电状态状态，Socmax和Socmin为Soc的最大值和最小值；μES为储能的自放电效率；Soc(t-1)为t-1时间内储能充电状态状态；QES为储能的总投资容量；Soc(t0)和Soc(tN)为调度周期初始和末尾的Soc。

储能充放电过程中，储能电压与电流都会发生变化。为了避免储能充放电时出现电流过大和电压过低的现象，提出一种储能能量分区控制策略，将储能充放电区间分为6个阶段，分别为[Soc0-Socmin]、[Socmin-Sochigh]、[Sochigh-Socmax]、[Socmax-Soclow]、[Soclow-Socmin]、[Socmax-Soc1]。在[Socmin-Socmax]区间采用快速充电、慢速充电、快速放电以及慢速放电4种充放电方式。

当储能Soc值处在[Soc0-Socmin]和[Socmax-Soc1]区间时，储能停止工作，进入待充电和待放电状态。

当储能充电时，若Soc值处在[Socmin-Sochigh]区间时，储能将进入快速充电状态；若储能Soc值处在[Sochigh-Socmax]区间，将停止快速充电进入慢速充电状态。

当储能放电时，若Soc值处在[Socmax-Soclow]区间，储能将进入快速放电状态；若储能Soc值处在[Soclow-Socmin]区间，将停止快速放电进入慢速放电状态。

储能控制策略流程如图3。

图3 储能控制策略流程框图

3.3 求解方法

采用粒子群算法对模型进行求解，种群个体规模数和最大迭代数分别为50、99。内层嵌入粒子群算法对设备与储能运行进行求解，简化问题的复杂度，提高模型的求解速度，求解流程如图4所示。

图4 求解流程框图

4 算例分析

4.1 算例配置与配置结果

算例参考文献[7,18-19]，以某地全年风机和光伏出力数据和负荷为依据。考虑风光不确定性，将全年场景划分为夏季(90 d)、过渡季(180 d)、冬季(90 d)。微电网电价设峰、谷、平3个时段，分时电价[20]数据见表1，并配置分布式光伏机组、分布式风机机组及储能对电负荷进行供给。锂离子储能损耗系数参考文献[21]，B1、B2、B3分别为30 330、19 300、12 000，a1为31 700，a2为370.3，R为 8.314，z为0.55。

表1 分时电价

设定规划周期为10 a，贴现率为0.07，储能残值率为6%。各个设备的运行参数如表2所示，设备成本参考文献[22]，见表3。

表2 设备运行参数

表3 设备成本 元·kW-1

本文考虑4种配置方案：

方案1：考虑多因素储能寿命损耗，采用储能控制策略对微电网进行设备容量配置；

方案2：考虑多因素储能寿命损耗，不采用储能控制策略对微电网进行设备容量配置；

方案 3：不考虑多因素储能寿命损耗，采用储能控制策略对微电网进行设备容量配置；

方案 4：不考虑多因素储能寿命损耗，不采用储能控制策略对微电网进行设备容量配置。

分别求解各个方案下的设备配置方案，最优适应度进化曲线见图5，配置结果见表4。

表4 配置结果

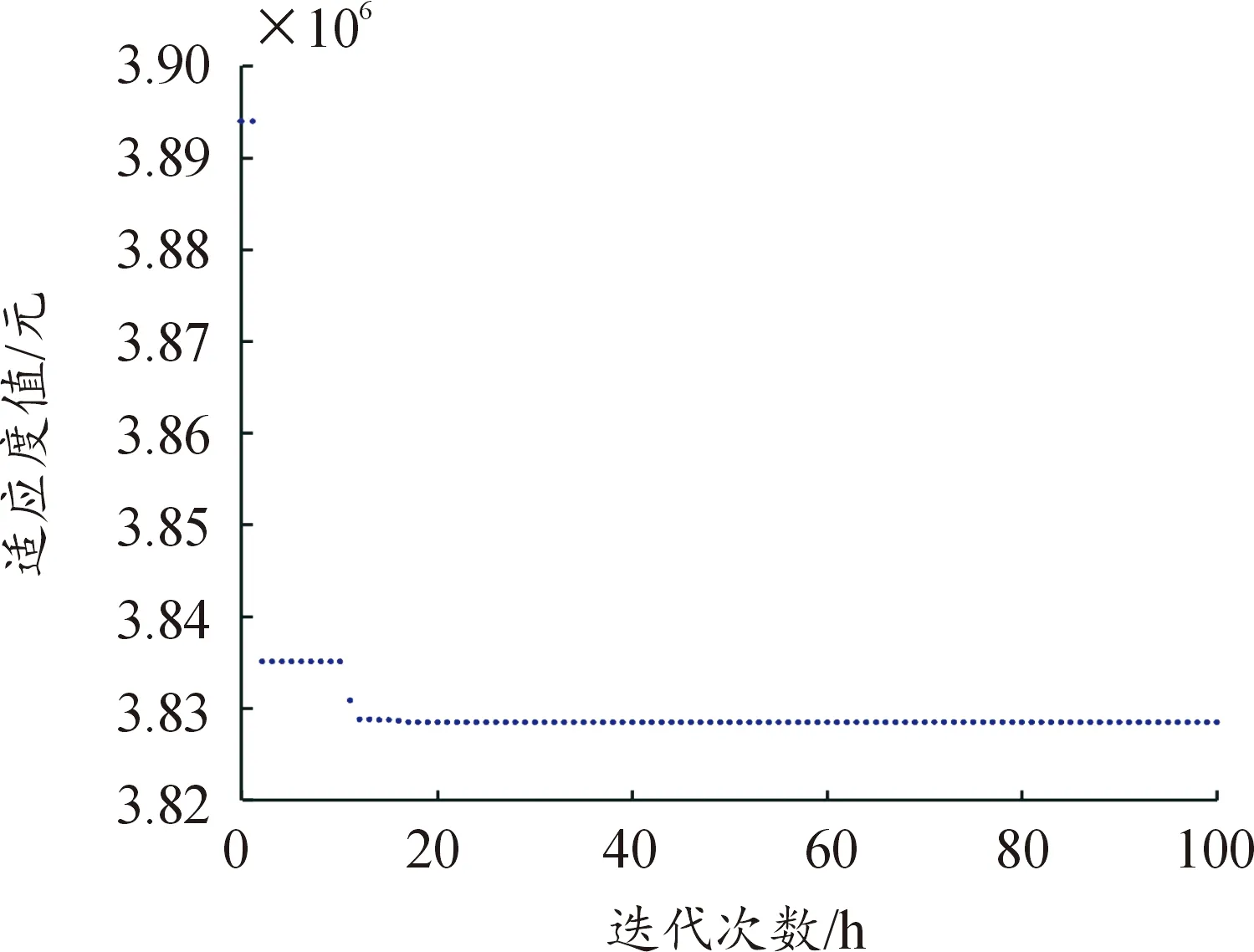
图5 粒子群收敛曲线

各方案储能Soc曲线见图6，储能寿命衰减情况见图7。

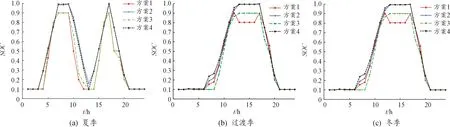
图6 储能Soc曲线

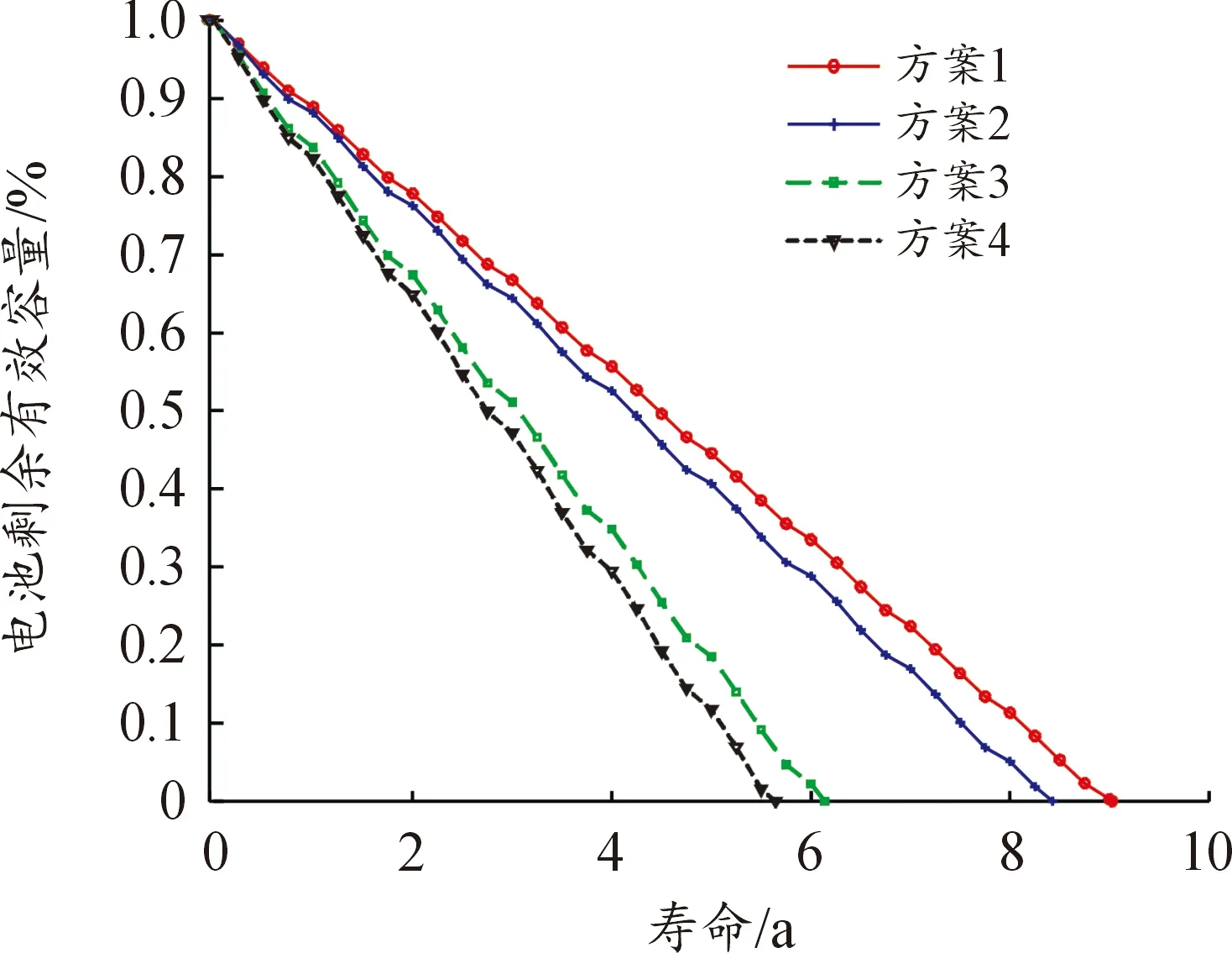
图7 储能寿命衰减曲线

4.2 算例分析

1) 对比配置结果，4个方案的风力发电机的配置容量没有变化，方案2和方案4的储能和光伏配置容量相比方案1和方案3有一定的增幅。从储能Soc曲线来看，对储能实能量管理使方案1和方案3的Soc曲线更平缓，由于方案2和方案4的储能为固定的充放电幅度，使得储能的使用寿命大大减少，储能的经济性降低。从储能的使用寿命来看，方案1储能的使用寿命为9.025 2 a，比方案2提升了7.08%，相比方案3和方案4提升了47.05%～49.32%。由于方案1和方案2考虑了多因素对储能寿命的影响，使得储能的容量配置更加符合微网的使用情况，避免了投入运行后出现储能提前报废的现象。算例分析表明，考虑多因素储能寿命损耗和实施储能能量管理策略可以更合理地配置微电网设备容量，解决了因配置容量过大或过小造成的资源浪费问题。

2) 从经济性来看，虽然方案1的年运行维护费用比其他方案高，但储能置换费用比其他方案少，其中方案4的储能置换费用高达132.30万元。最终方案1的等年值投资成本最少，说明本文所提方法能够提高系统的经济性。

5 结论

考虑多因素聚合的储能寿命，以投资置换成本量化储能系统的寿命损耗，制定储能控制策略，兼顾投资建设、运行调度和设备寿命折损等多方面经济性，构建以等年值投资成本和运维成本最小为目标函数的双层优化配置模型。通过对比4种配置方案，证明本文所提模型及储能控制策略能有效提升微电网规划和运行的全寿命周期经济性，缓解储能衰减，减少因容量配置不合理而造成的经济损失。