面向翻唱歌曲识别的改进相似度网络融合算法

朱东辉，陈 宁

(华东理工大学 信息科学与工程学院， 上海 200237)

0 引言

由于在音乐检索、音乐版权管理和授权、音乐创作辅助等方面的潜在应用，识别特定曲目的不同版本、表演或再现的翻唱歌曲识别(cover song identification,CSI)技术已经成为音乐信息检索(music information retrieval,MIR)领域的一个热门话题[1-2]。与原唱相比，翻唱歌曲可能涉及一些复杂的变化，如音调的转换、音乐整体结构的变化和节奏的变化等。这些变化使CSI成为一项具有挑战性的任务。

目前翻唱歌曲识别的过程涉及2个环节：特征提取和相似度度量。特征提取方法主要分为提取基于传统音频信号处理的手工特征[2-3]和提取基于深度神经网络的高阶特征[4-6]。在相似度度量方面则主要是通过融合来提升性能。根据融合对象的不同，融合方法可以分为对特征的融合和对特征间相似度的融合。例如，Doras等[3]利用一个双分支网络将2个不同特征经过不同的预训练模型进行处理后进行拼接构成一个更好的特征；Fan等[7]对基于声音级轮廓(harmonic pitch class profile,HPCP)[8]特征和基于主旋律(MeLoDy,MLD)[9]特征的相似度矩阵通过相似度网络融合(similarity network fusion,SNF)[10]算法进行融合；Jiang等[11]则是利用网络层不同阶段的特征向量计算互相似度矩阵，通过卷积层对相似度矩阵进行处理和拼接达到融合的效果。尽管基于深度学习的融合方法表现出了不错的性能，但是随着网络的规模和数据量的增大，训练的时间和算力成本也会成倍增加。且在翻唱识别的实际应用场景中由于版权原因往往无法获取足够的数据。因此，类似文献[7]的方法以其较低的计算复杂度仍具有一定的竞争力。

然而，文献[7]基于SNF的算法有以下局限性：第一，由于SNF只能融合方阵，而2个不同长度的歌曲构造的互相似度矩阵为非方阵，于是必须通过引入额外的自相似度矩阵来构造方阵以实现融合，增大了算法的时间复杂度。同时拼接引入的无关矩阵会影响融合矩阵的性能。第二，在传统的SNF中，由表征性能差的音频特征构造的核矩阵的负面影响会在多次迭代过程中逐步放大，从而影响融合效果。

为了解决上述问题，提出改进相似度网络融合(modified similarity network fusion,MSNF)算法。针对问题一，利用自相似度矩阵自建核矩阵从而实现对非方阵的融合，突破了SNF只能融合方阵的限制，避免了由于矩阵拼接和拆分造成的额外计算开销，同时也消除了拼接时所引入的无关矩阵的负面影响；针对问题二，利用SNF对基于不同特征的核矩阵进行融合，避免性能差的核矩阵的负面影响的延伸。本文的主要贡献为：第一，提出了泛化能力更强的MSNF算法，支持对任意尺寸矩阵的融合；第二，MSNF增加了融合的鲁棒性。利用融合核矩阵代替核矩阵，即使性能较差的核矩阵也不会对融合结果造成直接影响。为了验证MSNF的有效性，将MSNF替换文献[7]中所提出的CRP-SNF-MKI中的SNF融合算法。实验结果表明，基于MSNF的改进方法可在提升翻唱识别准确率的同时大幅降低算法时间复杂度。

1 SNF算法

SNF算法[10]被用于对基于不同特征的相似度方阵P进行融合。而S是由P通过K近邻技术得到的稀疏矩阵，仅包含每个节点与K个邻近节点的相似度。在融合过程中，该算法总是以P为初始相似度矩阵，以S为核矩阵，这既是为了捕捉图的局部结构信息，也是为了提高计算效率。

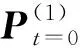
(1)

(2)

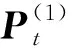
(3)

由于S是P的K近邻图，因此S和P是同样大小的方阵，于是如式(1)(2)所示，S可以通过直接转置的方式在迭代时分别在P左右进行矩阵相乘的运算。这也是SNF算法要求融合的矩阵必须为方阵的原因。而当该算法应用于非方阵的融合时，一个通常的做法是：引入多个无关矩阵对融合的相似度矩阵进行拼接从而构成大的方阵。这也导致了以下问题：一方面，由于P的拼接导致S也随之扩大，因此在进行矩阵乘法时运算量呈指数倍上升；另一方面，S的质量完全由P决定，因此在迭代时当相似度矩阵P质量不高时，整体算法的性能是较差的。针对以上2个问题，对SNF算法进行改进，并应用于翻唱识别任务中。

2 本文算法

翻唱歌曲识别流程如图1所示，虚线框内的部分是所提出的算法。

首先，分别从每个歌曲提取HPCP和MLD特征；其次，根据每个特征构造每个歌曲的递归图(recurrence plot,RP)和任意2个歌曲的交叉递归图(cross recurrence plot,CRP)分别作为自相似度矩阵和互相似度矩阵；然后，利用MSNF对每两首歌曲的2种不同特征进行融合，得到融合的CRP；最后，基于融合后的CRP计算相似度，并利用多核整合(multiple kernel integration,MKI)进一步修改相似度得分，依据最终得分判断是否为翻唱。

2.1 特征提取

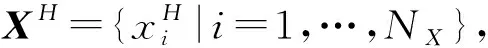
(4)

式中：D表示嵌入的维度，τ表示时间延迟。

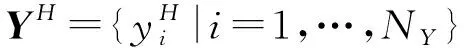
2.2 RP图和CRP图构建

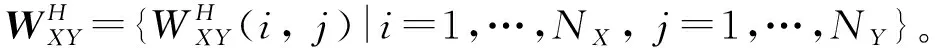
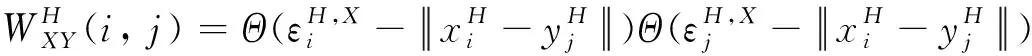
(5)

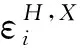
2.3 MSNF

相较于SNF算法，MSNF的改进主要体现在2个方面：基于融合对象不同，分别构造自相似度矩阵作为核矩阵完成非方阵的融合；对基于不同特征的自相似度矩阵进行融合以提高算法鲁棒性。

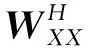
(6)

为了获得局部相似性来代替全局相似性，利用式(7)，通过K近邻技术来得到歌曲X对应的核矩阵，记为QXX={QXX(i,j)|i,j=1,…,NX}。

(7)

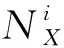
(8)

(9)

式中：×为矩阵的向量积。利用式(10)对二者进一步融合，从而得到PXY={PXY(i,j)|i=1,…,NX,j=1,…,NY}。

(10)

2.4 相似度计算和多核整合

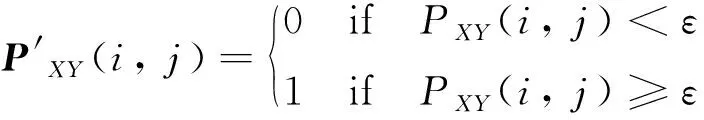
(11)

式中：ε为相似度阈值。然后假设累积矩阵表示为C={C(i,j)|i=1,…,NX,j=1,…,NY}。当i=1,…,NX和j=1,…,NY时初始化矩阵C(i,1)=C(i,2)=C(1,j)=C(2,j)=0，那么累积矩阵C可以由式(12)计算得到。

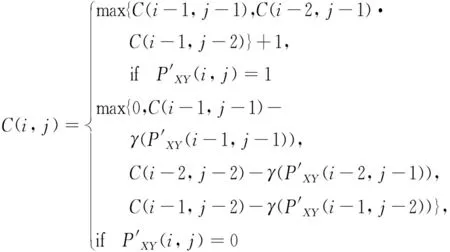
(12)

式中：i=3,…,NX；j=3,…,NY；γ(·)为惩罚函数，可利用式(13)计算。

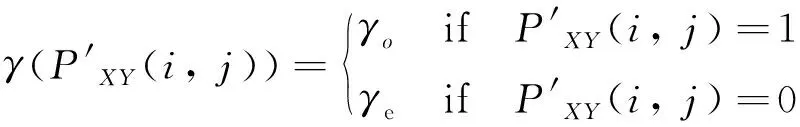
(13)

式中：γo为起始的惩罚系数，设置为5；γe为延伸的惩罚系数，设置为0.5。

将歌曲X和歌曲Y之间的相似度定义为累积矩阵C中所有元素的最大值，即Cmax=max(C(i,j))。最后，利用式(14)对歌曲X，Y之间的相似度进行标准化处理，得到d(x,y)：

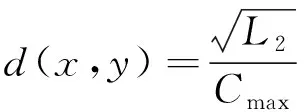
(14)

式中：x和y表示两首不同的歌曲；L2为两首歌曲中较长音频的帧数；d数值越小，表示两首歌曲越相似。为了进一步提高性能，采用SIMLR[13]中的MKI进一步优化得到的相似度得分。

设整个数据集所有歌曲间的互相似度矩阵为S={S(x,y)|x,y=1,…,NSong}，其中NSong表示数据集中的歌曲数。S(x,y)由式(15)优化得到。

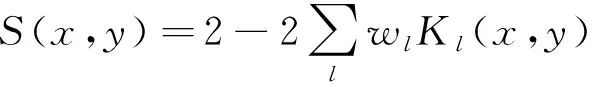
(15)

式中：Kl为高斯核函数，由式(16)计算得到，wl为l个高斯核函数的权重。

(16)

式中：KNN(x)表示歌曲X前n个近邻的集合，σ和n以及整体的优化目标函数同文献[13]一致。

最终，将得到的相似度矩阵S用于翻唱识别任务。

3 实验结果

3.1 数据集介绍

为了验证所提出模型的优越性，本文中采用了3个翻唱数据集，分别为Covers80[14]、 Covers40[1]和Covers273，其中Covers80包含80组翻唱歌曲，每组包含一首原唱和一首翻唱歌曲；Covers40包含40组翻唱歌曲，每组包含一首原唱和九首翻唱歌曲；Covers273是翻唱歌曲公开库Second Hand Song (SHS)的一部分，包含273组翻唱歌曲，每组内包含的翻唱版本数量不定，平均每组3首歌。

3.2 评估指标

为了验证所提出的MSNF算法相比于传统SNF算法的优越性，以及相对于基于单一相似度函数或相似度融合[7]的最新CSI方法的性能提升，采用3个评价指标，即平均准确率均值(mean average precision,MAP)、前10条最相似的音乐信息TOP10和受试者工作特征曲线(receiver operating characteristic curve,ROC)下面积(area under curve,AUC)。这3个评价指标值越大表示算法性能越好。

3.3 识别准确率对比

表1列出了在3个数据集上，本文算法(记为CRP-MSNF-MKI)与其他基于机器学习的翻唱识别算法的准确率。这里，CRP-MSNF-MKI是将文献[7]方法中的SNF模块替换为MSNF得到的。可以看出，本文算法明显优于CRP-SNF-MKI，证明了MSNF改进的有效性。此外，除了在Covers80 数据集上，本文方法的MAP值略低于Early-Late[18]方法外，在3个数据集上，无论采用哪种衡量标准，本文的方法均优于其他方法。而Early-Late方法唯独能够在Covers80 上取得很高的MAP值的主要原因为该模型所融合的特征均为节拍同步特征，而Covers80 数据集中的多数样本均具有鲜明的节拍特征。

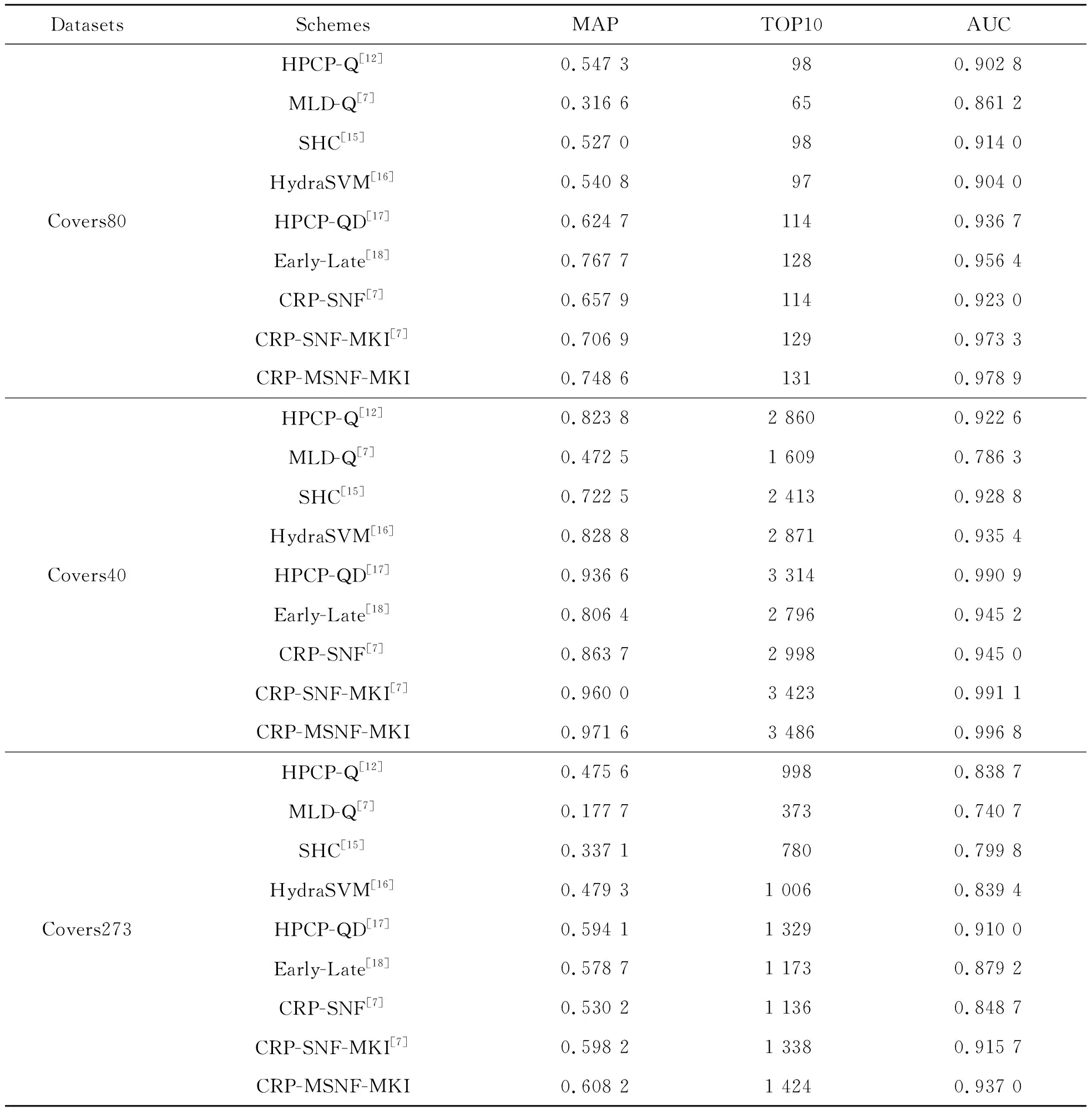
表1 识别准确率

图2显示了在Covers40数据集上，融合前后翻唱歌曲的聚类效果，其中(c)为将(a)(b)所用特征用本文算法进行融合后的聚类效果。可以看出，相比于基于单一特征的相似度模型，CRP-MSNF-MKI模型可以有效提升聚类的效果，集中表现在对(a)中错误分类样本的纠正以及对(b)中某些簇聚合效果的提升。

图2 在Covers40上聚类效果

表2列出了本文的方法和基于深度学习的翻唱识别方法性能参数。可以看出本文的方法优于文献[19]和文献[20]提出的深度学习的方法，但低于文献[6]的方法。然而，由于基于深度学习的方法需要大量的训练数据作为基础。因此，本文的方法仍然具有一定的优势。

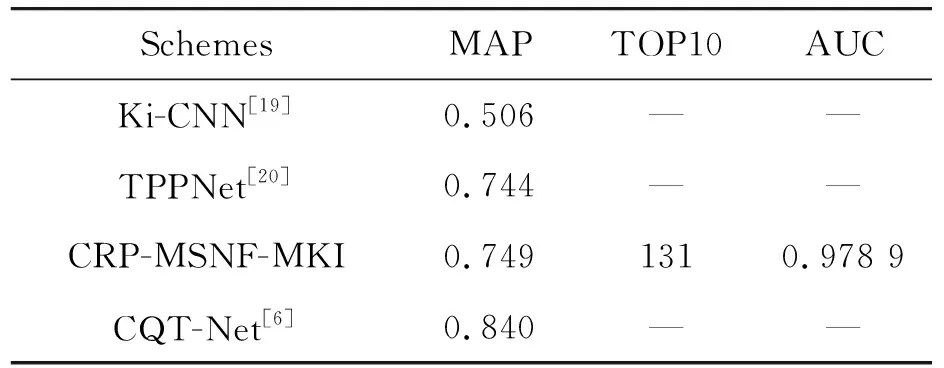
表2 本文方法与深度学习网络在Covers80上的性能参数

3.4 超参数的影响

MSNF采用嵌套融合的方式预先融合了核矩阵，之后再对互相似度矩阵进行融合。为了探究融合超参数对识别准确率的影响，在Covers80上对不同超参数作用下的MAP值进行了对比。如图3所示，其中每个子图的横轴表示核矩阵进行预先SNF的迭代次数t′，纵轴表示邻近帧数k′。整体的横轴表示MSNF迭代次数t，纵轴表示邻近帧数k。

图3 Covers80数据集上MSNF超参数对MAP的影响

通过展示部分参数的数据可以看出：第一，随着MSNF迭代次数的增加，MAP呈现增大的趋势，证明了融合的有效性。第二，对于核矩阵的融合来说，往往只需迭代一次就能达到最好的效果，而多次的迭代反而会使性能有所下降。

3.5 时间复杂度对比

由于本文的MSNF解决了传统SNF只能融合方阵的局限性，使得对于非方阵的融合过程大大简化。而CRP-SNF-MKI[7]为了满足方阵的需求进行了多个矩阵的拼接，对得到的大矩阵进行融合后又进行拆分，所消耗的时间较多。表3对比了在相同实验环境和实验参数下Covers80数据库上基于SNF和基于MSNF融合所消耗的时间。可以看出本文算法的时间复杂度为SNF的1/9。

表3 算法时间

4 结论

针对SNF的缺陷提出改进模型，并将其应用于翻唱歌曲识别任务。实验结果表明，本文方法在识别性能和时间复杂度方面均优于SNF。需要说明的是该融合方法由于解决了只能融合方阵的限制，极大增强了算法的泛化性，因此也适用于其他基于多视图融合的分类任务和检索任务，例如图像分类、癌症亚类识别以及药物分类等。