稀疏表示自编码网络的齿轮平稳型故障特征提取研究

郑 琛，丁 康，何国林,2，蒋 飞，叶 鸣

(1.华南理工大学 机械与汽车工程学院， 广州 510640； 2.人工智能与数字经济广东省实验室， 广州 510640； 3.广州华工机动车检测技术有限公司， 广州 510640)

0 引言

信号特征提取是定轴齿轮故障诊断的基础，在复杂恶劣的工况下实现高精度的特征提取，可以为后续分析提供有力依据，具备重要的工程应用价值。

神经网络因其强大的特征学习能力[1-3]，在故障诊断领域得到了越来越广泛的应用。但神经网络提取的抽象特征不具备可解释性[4]，为提取具备鲁棒性的特征，需要大量样本进行特征学习，实际工程中难以实现。针对该问题，有学者尝试将信号处理方法与神经网络结合，使神经网络部分结构在信号时频特征层面具备可解释性，从而提高特征的敏感性[5-9]。Yang等[5]将优化粒子群算法与小波基函数结合，通过优化小波基函数尺度与时刻参数提取与信号时频特性相关的特征，其编码层在信号时频特征层面具备可解释性，可以提取信号的敏感特征。Qu等[6]在输入层对信号进行短时傅里叶变换与分段频谱特征分析，使编码层特征提取过程具备可解释性，实现了小样本量下的机械健康状态特征提取。Li等[7]用小波函数代替卷积核，使第一层卷积层具备可解释性，从而提高特征的时频敏感性。但以上方法得到的仍是抽象特征量，无法为诊断结果提供物理依据。

信号稀疏表示方法对于故障信号特征具备强大的表征能力。稀疏表示方法通过少量元素在特征空间中重构出目标信号[10-12]，随着齿轮传动系的故障信号特征研究[13-14]与故障模型更新[15-16]，有学者尝试提取故障信号中有物理意义的特征量。Sun等[17]基于齿轮故障模型，改进稀疏表示方法，提高了信号重构的精度。Wang等[18]基于旋转设备机理模型设计字典，通过稀疏分解实现旋转设备的故障分类。Fan等[19]基于齿轮故障响应机理设计小波字典，提取出齿轮故障信号的特征分量。Tang等[20]基于隐成分分析设计稀疏分解方法，提取早期微弱故障特征。何国林[21]使用相关滤波法，通过相关性匹配特征参数构造字典，实现了具备物理意义的平稳型故障特征提取过程。随着研究深入，稀疏表示方法可以提取定轴齿轮平稳型故障信号的特征参数，但该类方法基于相关滤波法得到的解析字典无法自适应优化，存在精度限制，且稀疏表示方法通过故障信号中提取的谐波分量结合人工频谱分析获得平稳型故障特征，无法直接提取平稳型故障特征参数。张明[22]通过分析实验证明传动系中存在偏心设备时，系统响应信号会存在与故障无关的干扰谐波分量，此时稀疏表示方法会提取干扰分量，影响后续频率特征分析。

综上所述，与稀疏表示方法结合可使神经网络特征学习过程具备可解释性，通过神经网络将原始输入映射为本质特征的深度学习能力，可直接提取高精度的平稳型故障特征参数，实现两者优势的互补。在神经网络中，自编码网络可以实现故障信号的特征提取与重构[23-24]，与稀疏表示方法具备相似的算法逻辑，两者具备理论上的通性。本文研究目标为结合定轴齿轮平稳型故障机理模型，基于稀疏表示方法的物理意义赋予自编码网络可解释性，实现定轴齿轮平稳型故障信号的降噪重构，提取平稳型故障响应信号的高精度特征参数。

1 定轴齿轮平稳型故障响应机理、稀疏表示原理及自编码神经网络模型

定轴齿轮发生周布型损伤时，齿轮啮合振动的幅值发生变化，产生平稳调制信号，通过式(1)可以模拟定轴齿轮平稳型故障信号[16]。

cos(2πifzt+φi)+η(t)

(1)

式中:A为对应谐波原子的幅值，φ为对应谐波原子的相位，fz为啮合频率，其对应阶次为i，fn为故障轴转频，故障轴转频阶次为j，η(t)为噪声分量。

对式(1)进行三角函数转化可得式(2)[21]为

(2)

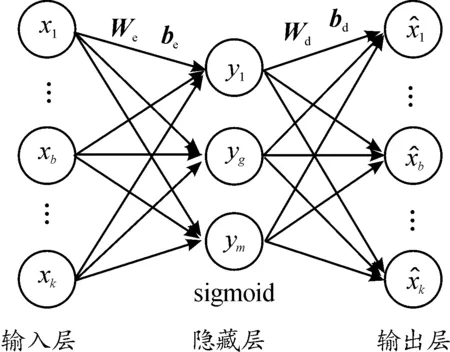
图1 自编码神经网络结构示意图

信号稀疏表示原理[12]如式(3)所示，O为原始信号，D为过完备字典，a为稀疏向量，‖a‖0为0范数，表示a的稀疏程度，ε≤ 0是近似稀疏的容差，信号稀疏表示方法通过最稀疏向量a与过完备字典D在一定精度下重构信号O，实现信号稀疏表示，稀疏表示过程包括字典构造与稀疏向量求解。

(3)

2 稀疏表示理论融合自编码网络

在自编码网络中，将编码过程等效稀疏向量求解，解码过程等效信号重构，解码层权值矩阵Wd等效字典矩阵D，编码向量y等效稀疏向量a。神经网络每一次迭代，都完成了一个字典学习(解码层矩阵更新)、稀疏向量更新(编码层矩阵更新)、信号重构的过程，控制解码层矩阵在适当的特征空间内生成与更新，使自编码网络具备可解释性。将构成平稳型故障信号的谐波原子表示为

dm(t)=cos[2π(ifz±jfn)t+φm]

(4)

通过神经网络算法优化原子特征参数，从而实现直接对平稳型故障本质特征参数(啮合频率fz、故障轴转频fn)进行提取，故障响应可以表示为谐波原子的线性叠加，代入式(2)为

(5)

式中:A为原子幅值向量，dm(t)为某一特征参数下的故障响应信号原子，m为原子阶数，F(fz,fn,φm)是原子在特征参数维度上的函数式同式(4)，解码层矩阵由3组参数生成，具备物理意义。该自编码网络实现了信号稀疏表示过程，命名为稀疏表示自编码网络，其结构如图2所示。

图2 稀疏表示自编码网络结构示意图

根据平稳型故障信号特征，为保证幅值求解范围，编码层不设激活函数。其参数更新图如图3所示，更新变量包括We、be与参数向量组fz、fn、φm，损失函数为均方误差函数，达到一定重构精度时，解码层的特征参数即为该故障系统的特征量，实现了定轴齿轮系平稳型故障信号的降噪重构。

图3 神经网络参数更新图

3 神经网络算法设计与模型搭建

通过链式法则实现特征参数的更新，特征参数偏导公式为

(6)

(7)

(8)

根据链式求导法则，将参数偏导式乘上损失函数对字典原子的偏导式得到式(9)，式中，MSE为损失函数，F为解码层字典矩阵原子，S为对应参数的步长。

(9)

根据原子阶数m、每阶啮合频率及其调制边频总阶数M可以得到求解啮合频率阶次i与调制频率阶次j的公式(10)，其中∥为整除，%为取余。

i=(m-1)∥M+1

j=(m-1)%M-(M-1)/2

(10)

3组参数梯度值差异较大，工程中常见特征参数及其原子对参数偏导梯度的均值数量级见表1，可见数量级存在较大差异，无法通过单一步长使所有参数得到有效优化。针对该特征，将参数按数量级差异分步激活为变量参与更新，分别适配学习率，提高收敛速度。

表1 特征参数数量级表

基于算法优化后的神经网络，根据定轴齿轮平稳型故障特征设计N+1层深度稀疏表示自编码网络如图4所示，进行齿轮平稳型故障信号的降噪重构与高精度的特征提取。

图4 深度稀疏表示自编码网络图

隐层神经元数：从原始信号中截取分析信号xr，输入神经网络做特征提取，根据原子阶数m设定隐藏层神经元数量。将涵盖信号主要故障频率成分的频率范围上界称为最大分析频率fh，为减少计算涉及的频率特征量，将fh取为接近最高故障频率成分的值，根据原始信号频谱确定fh与啮合频率阶数k，fh与k以及参数M存在关系式[21]为

fh=kfz+(M-1)fmin/2

(11)

式中:Mh=(M-1)/2为最大边频阶次，fmin设为系统最小转频，从而使得到的M为最大值，以保证充分提取平稳型故障响应成分，原子阶数m=k×M，在神经网络收敛后，冗余谐波阶次幅值为0。

平稳型故障信号提取：系统可能存在N个平稳型故障源，如一对啮合齿轮就存在两个潜在的平稳型故障源，设定稀疏自编码神经网络层数为N，以保证提取出所有的平稳型故障。为防止提取到无关频率成分，根据系统转频进行决策，对非系统转频成分幅值置0，而后将故障信号残差输入下一层，完成N层平稳型故障特征提取后，隐藏层幅值非0的参数即为平稳型故障特征参数。

剔除干扰谐波分量：在部分设备中齿轮系故障信号会存在干扰谐波[22]。神经网络会将大幅值噪声分量以谐波的形式重构，也会在平稳型故障信号重构过程中引入干扰谐波。在平稳型故障特征提取层中，干扰谐波分量无法通过啮合频率与转频的特征公式重构，保证了故障特征参数提取的精度。

而在信号处理工程中通常需要剔除干扰谐波分量[21]，故增设干扰谐波成分提取层。神经网络如图5所示，该层神经网络谐波原子为公式(12)，变量为干扰谐波频率fm，算法与平稳型故障提取层相同，从而剔除残差信号中的干扰谐波成分，进一步保证输出的重构信号为平稳型故障信号。

图5 干扰谐波成分提取层网络结构图

4 仿真验证

单级定轴齿轮箱特征参数见表2，设定输入轴转频为30 Hz，啮合频率fz为780 Hz，幅值与相位随机生成，采样频率fs设为20 480 Hz，采样时间0.2 s，故障信号有3阶啮合频率，每阶啮合频率受到1阶转频调制，假定输入轴齿轮出现平稳型故障。

表2 仿真定轴齿轮箱参数

为模拟实际工程中机械设备特性产生的干扰，在信号中加入干扰谐波，频率为770、800、1 500 Hz，相位与幅值随机生成，并加入冲击响应成分。为模拟实际工程中的噪声干扰，加以-10 dB的高斯噪声，表达式为

SNR=10log(PS/PN)=-10 dB

(13)

式中：SNR为信噪比，PS为系统响应信号的功率谱，系统响应信号包括平稳型故障响应、冲击型故障响应与机械设备产生的干扰谐波成分，PN为噪声功率谱。实际工程中，-10 dB信噪比的噪声对信号的干扰比多数工况的噪声干扰更严重，通过-10 dB加噪信号的重构与特征提取来验证所提方法在恶劣工况下的抗噪性能。得到故障信号分别如图6、7所示。

使用所提方法提取信号的平稳型故障成分，如频谱图6图(b)与图7(b)所示，故障信号有3阶啮合频率，红色虚线为最大分析频率fh= 2 380 Hz，最小转频为fmin=20.53 Hz，根据式(11)可得M=5，原子阶数m=3×M=15。

图6 无干扰信号及其频谱

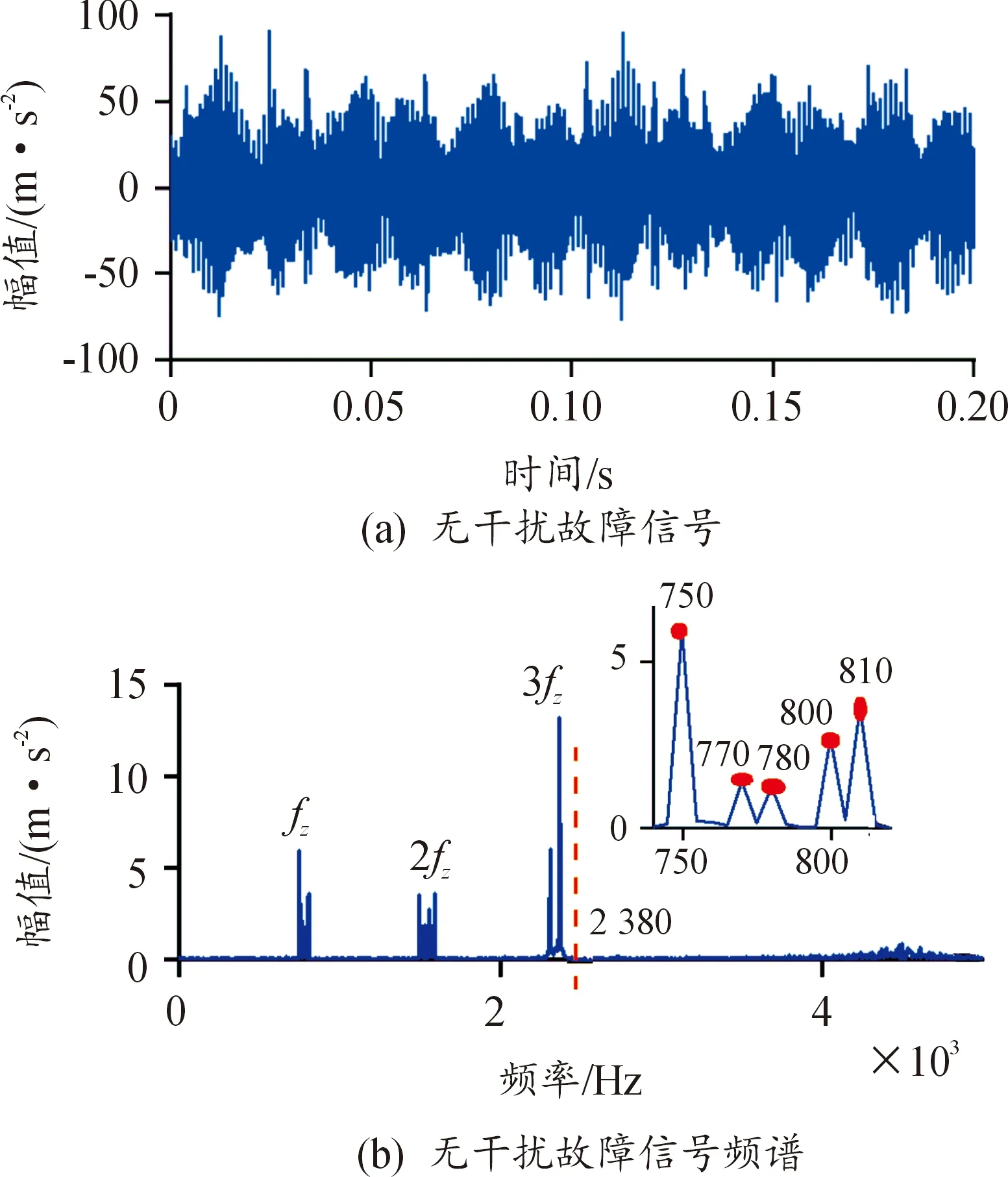
图7 受干扰信号及其频谱

所提方法通过解码层学习定轴齿轮箱平稳型故障特征参数，传统神经网络通过提取信号的抽象特征在分类层实现故障诊断，两者实现的功能存在差异，难以进行对比，而基于相关滤波的稀疏表示方法[21]可以较高精度地提取平稳型故障信号的物理特征参数，与所提方法实现的功能近似，故在以下仿真与实验中将其作为对比方法。对比方法的4组初始参数中频率原子为fc=[0∶0.01∶fh]，相位原子为φc=[-π∶0.01∶π]，啮合频率阶数k与所提方法相同为3阶，最大边频阶次为Mh= (M-1)/2=2。所提方法及对比方法重构信号如图8所示，图8(a)、(b)为所提方法提取的平稳型故障信号，(c)为对比方法的受干扰故障信号重构图，从图中可以看出，所提方法可以分离接近啮合频率的干扰谐波成分，单独提取平稳型故障信号，而对比方法会重构所有的谐波分量，忽略干扰谐波成分，从对比方法提取的特征量中筛选平稳型故障特征，其重构信号如图8(d)。

对图8(a)、(b)、(d)截取时间段(0.100,0.104)得到放大图9，从图中可以看出所提方法在严重干扰下仍然有着较高的重构精度，且重构精度高于频率成分筛选后的对比方法。将所提方法提取的特征参数及其误差均值列入表3。从对比方法获得的特征参数中提取平稳型故障相关参数并计算其平均误差列入表4。通过与原无噪声仿真信号的均方误差体现信号重构精度与整体参数精度。

图8 信号重构图

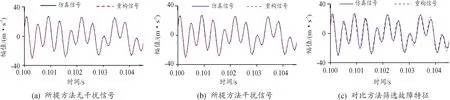
图9 局部信号重构放大图

表3 所提方法特征参数及误差

表4 对比方法筛选后特征参数及误差

从表中可以看出，对比方法提取谐波成分的频率，所提方法直接提取平稳型故障特征参数。对比2种方法故障特征参数的精度，信号重构精度、频率参数精度和相位参数精度都得到了提高。

在信号受干扰仿真中，任意提取一行解码层矩阵原子如图10所示，可见解码层矩阵由各平稳型故障的谐波原子F(fz,fn,φm)构成，神经网络直接提取了定轴齿轮箱的平稳型故障特征参数，其故障信号重构与特征学习过程具备可解释性。

fz= 780.0 Hz, fn= 30.0 Hz, φm=2.79图10 某行解码层矩阵原子图

5 实验验证

单级定轴齿轮箱平稳型故障实验在传动实验台上进行，输入轴转速为800 r/min，输出轴齿轮存在平稳型故障，设置采样频率为51 200 Hz，单级定轴齿轮箱参数见表5，实验设置如图11所示。

表5 实验定轴齿轮箱参数

图11 实验台架图

实验信号如图12(a)所示，截取分析信号段如图12(b)，分析信号频谱如图12(c)所示，信号主要啮合频率阶数为k=8，第8阶啮合频率放大后得到最大分析频率fh=2 590 Hz，最小转频fmin=5.7 Hz，根据式(11)得到每阶啮合频率及其边频总和阶数M=13，原子阶数m=k×M=104。

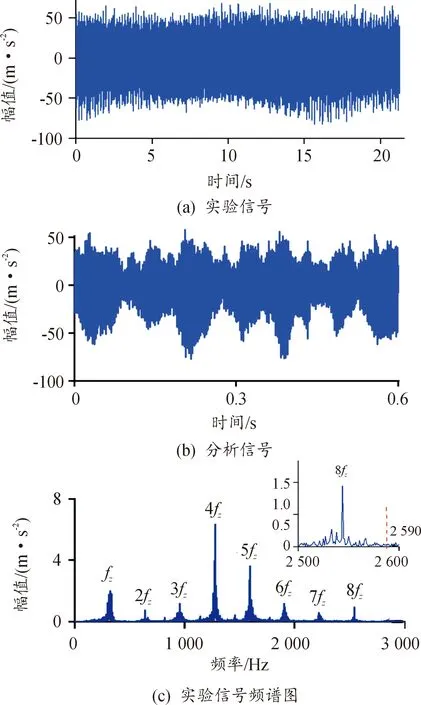
图12 实验信号图

对比方法频率原子为fc=[0∶0.01∶fh]，相位原子为φc=[-π∶0.01∶π]，啮合频率阶数k与所提方法相同为8阶，边频最大阶次为Mh= (M-1)/2=6。所提方法提取的平稳型故障响应信号如图13(a)所示，其整体幅值趋势与分析信号具有较高的拟合度，某行解码层原子如图14所示，神经网络特征学习过程具备可解释性，对比方法重构信号如图13(b)所示。

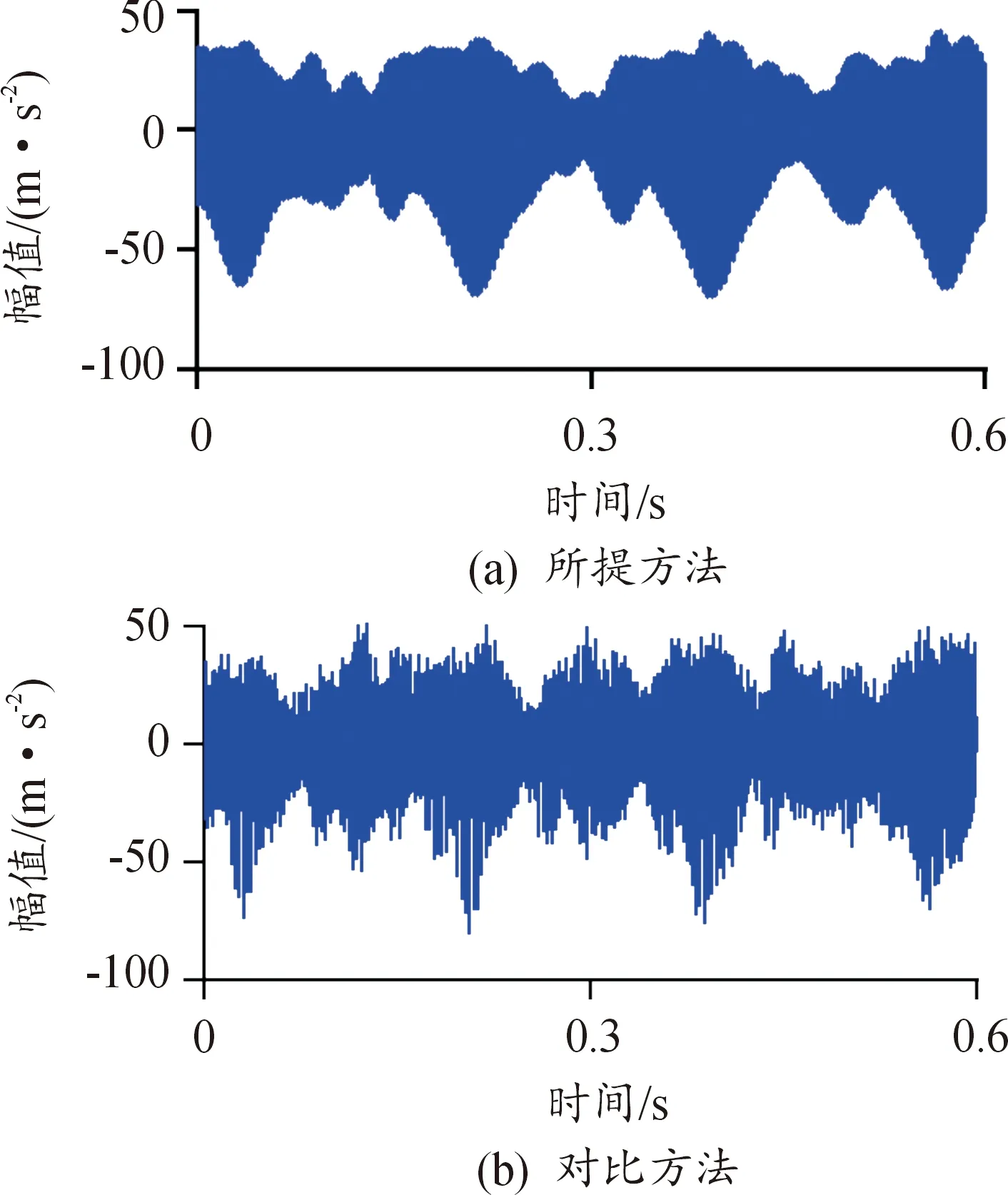
图13 重构信号图

图14 所提方法解码层矩阵原子图

所提方法提取的故障特征参数见表6，可见所提方法直接提取了平稳型故障特征参数，无需进行频谱分析，啮合频率为fz= 319.21 Hz，故障转频为fn= 5.83 Hz，忽略实验本身导致的误差，与故障系统特征频率320 Hz以及5.7 Hz接近，在实际工程中所提方法仍然有效。将对比方法提取的部分平稳型故障频率成分与干扰频率成分列入表7，可见对比方法无法剔除干扰频率成分，计算所有故障特征转频的均值为5.42 Hz，所提方法故障特征参数精度较对比方法有较大提升。

表6 所提方法特征参数及误差

表7 对比方法部分特征参数及误差

6 结论

1) 将自编码网络编码层等效稀疏向量求解，解码层等效字典学习，通过平稳型故障特征参数控制解码层变量的更新，设计了具备可解释性的稀疏表示自编码网络，用于提取定轴齿轮系平稳型故障特征参数。

2) 基于平稳型故障特征参数设计了优化算法，优化了信号重构与参数学习流程，基于平稳型故障系统特征搭建了深度稀疏表示自编码网络，实现了定轴齿轮平稳型故障信号高精度的降噪重构与特征参数提取。

3) 用所提方法对定轴齿轮箱平稳型故障进行了仿真分析，结果表明神经网络学习过程具备可解释性，提取了高精度的特征参数，分离了与啮合频率成分接近的干扰谐波成分，实现了齿轮平稳型故障信号的降噪重构，精度较对比方法有大幅度提高。通过定轴齿轮箱平稳型故障实验与对比证明了该方法的有效性。