履带车辆制动器扭振信号瞬时频率特征提取方法研究

周铖，罗杨，魏江，曹宏瑞，2，兰海，张万昊

(1.西安交通大学 机械工程学院，陕西 西安 710049;2.西安交通大学 机械制造系统工程国家重点实验室，陕西 西安 710049;3.中国北方车辆研究所，北京 100072)

0 引言

履带车辆因其良好的机动性能在现代军事、农业及建筑业都发挥着关键性作用［1-2］。随着我国综合国力的提升，科学技术以及军事力量也有极大的发展，为保证履带车辆在运输和战斗过程中具有更高的机动性能，履带车辆发动机也向高速大功率方向发展［3］，对于工况复杂的履带车辆而言，其制动器的扭振现象愈加显著。

发动机是履带车辆的核心，除提供动力外，也是扭振的激励源［4-5］。当发动机产生扭振后经过一系列的传动装置最终将激励传递到制动器，从而使得制动器发生扭振。制动器发生扭振对其可靠性是一个潜在的极大威胁，在很大程度上扭振会造成制动器制动效果降低甚至失效，从而引发事故。因此对制动器扭振的研究在履带车辆的研究中尤为重要，对其参数的测试不仅可以为制动器的内部尺寸设计提供参数，降低制动器的扭振幅值，并且能为履带车辆制动器中制动片的更换提供参考，保证履带车辆制动器在工作过程中的可靠性。

目前，测量扭振的方法还在不断发展的过程中，对于扭振信号的获取精度、有效的数据分析方法和扭振监测的实时性都需进一步得到提高［6-7］，尤其针对处于复杂恶劣、空间狭小结构紧凑的环境中的旋转部件。本文就某型履带车辆制动器的测试环境恶劣、工况复杂、干扰强等特点，展开了对履带车辆制动器扭振瞬时频率特征提取的研究，采用脉冲时序计数法［8-10］的扭振信号获取方法，研究基于参数优化变分模态分解(VMD) 的扭振信号瞬时频率特征提取方法，通过采用优化的VMD 算法实现对扭振信号的分解降噪以及重构，采用零点插值计算扭振信号两脉冲之间的时间间隔，完成对扭振信号瞬时转速波动信号的计算，而后采用频谱分析，提取扭振信号的瞬时频率特征。

1 扭振信号瞬时转速获取方法

1.1 扭振信号的测量原理

脉冲时序计数法扭振测量技术是利用安装在轴上的等分齿轮结构，通过非接触式磁电、光等传感器产生相应的脉冲信号［11］。码盘或等分齿轮每转过一定角度就会产生一个脉冲，测得两个脉冲间隔时间，就可获得两脉冲之间的平均角速度，进而获得扭转角和角速度差。当转轴不发生扭振时，转轴的瞬时速度等于其平均速度，传感器经过等分齿轮时输出的脉冲为等间隔的［12］;当转轴发生扭振时，相当于在转轴平均速度上叠加了转速波动，则传感器输出的脉冲为不等间隔的。

假设等分齿轮齿数为Z 个，则每个齿的分度Δθ 为

或用弧度制(rad) 表示Δθ 为

根据传感器输出波形可采用高频A/D 采样法［13］或高频计数法［14］求出转过第i 齿时的脉冲信号的周期Ti(s)，则转过第i 齿(i=1，2，3，…，Z) 时的瞬时转速ni为

由此可得转轴转过一周的平均转速为

则等分齿轮转过第i 齿的扭振瞬时转速波动为

1.2 扭振信号瞬时转速的提取

由1.1 节计算公式可知，扭振测量的关键是获取扭振信号周期和计算瞬时转速，瞬时转速的提取主要采用零点插值法［15-16］。

零点插值法是指通过线性插值的方式找到原始信号波形与零线的交点序列{p1，p2，…，pZ}，如图1所示。

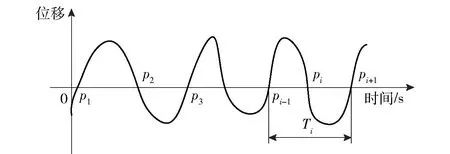
图1 零点法求瞬时转速示意图Fig.1 Diagram of instantaneous speed by the zero point method

分析图2 所示的信号片段，可知单个齿经过所产生的信号为pi-1至pi+1段。

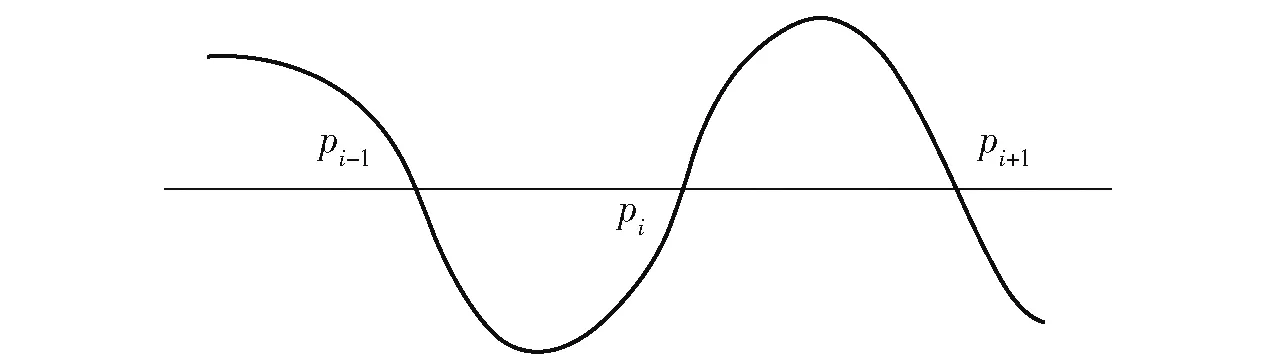
图2 线性插值零点法计算瞬时转速Fig.2 Calculation of instantaneous speed by the zero point linear interpolation method

转过第i 齿经历的时间为

式中:T 为采样卡采样周期。

第i 齿的瞬时转速为

2 参数优化VMD

2.1 VMD 算法基本原理

VMD 是一种非递归、自适应分解算法，每个本征模式分量(IMF) 分量的带宽和中心频率利用迭代确定［17］，由K 个IMF 组成的模态函数uk(t) (k=1，2，…，K) 的具体步骤如下:

1) 通过Hilbert 变换，得到各模态函数uk(t) 的解析信号，获得uk(t)的单边频谱uk(t)，δ(t) 为Dirichlet 函数，* 为卷积符号。

2) 进行频率混合，对各模态函数uk(t) 的解析信号混合一个预先估计中心频率{ω1，ω2，…，ωK}表示各IMF 分量的频率中心。将各模态的频谱变换到基频带

3) 通过高斯平滑解调信号获得每段带宽，即L2范数梯度的平方根。构造出约束的变分模型为

式中:{uk}={ u1，u2，…，uK} 表示分解得到的K 个IMF 分量;∂t为对函数求时间的偏导数;x(t) 为分解的主信号。

为求解上述约束的变分模型的最优解，引入惩罚因子α 构造增广Lagrange 函数为

式中:λ 为Lagrange 乘子;α 为惩罚参数;〈·〉表示内积运算;λ(t) 用来保持约束条件的严格性。

将上述Lageange 函数从时域转换到频域，并进行极值求解，可获得迭代n +1 次过程中模态分量在频域中的表达式，即

4) 使用交替方向乘子算法(ADMM)［18］进行约束变分模型的最优解的求取，将原始信号将被分解为K 个窄带IMF 分量。

具体算法如下:

3) 根据如式(13) 更新λn+1:

式中:τ 为正则系数。

2.2 参数优化VMD

由PSO 算法［19-21］的原理可知，PSO 能够根据适应度函数的最值作为优化准则来寻找VMD 算法的最优参数组合。利用PSO 搜寻VMD 算法的影响参数时，需确定一个适应度函数，粒子每次更新位置时计算一次适应度值，通过对比新粒子适应度值进行更新。本文基于扭振信号的特点采用能量熵［22］作为PSO 的适应度函数搜寻VMD 最优参数组合［Kopt，αopt］。

能量熵Lp为

式中:Lp(k) 表示第k 个IMF 分量的能量熵;pk表示第k 个单分量IMF 能量的归一化形式;E(k) 表示第k 个单分量IMF 的能量。

基于PSO 优化VMD 参数组合的主要操作步骤如下:

1) 定义粒子的位置和速度范围。设粒子群个体的位置对应VMD 算法参数［K，α］的一个候选解;初始化所有粒子位置和速度，并在设定范围内选取随机值，通过计算确定目标函数。

2) 确定PSO 算法的适应度函数，在不同位置对扭振信号进行VMD 运算，并采用式(14) 和式(15) 计算各IMF 的能量熵;

3) 根据式(16) 计算最小能量熵为局部极小值min Lp(k)，即VMD 的最优参数组合［Kopt，αopt］的一个候选解;

4) 比较不同位置的适应度函数值局部极小值min Lp(k)，并对个体局部极值和群体全局极值进行更新;

5) 对粒子的速度和位置进行更新。转至步骤2，直至达到预设迭代次数，输出最佳适应度函数值min Lp和粒子位置［Kopt，αopt］。

3 扭振信号处理流程

由扭振信号的测量方法可知，扭振的获取是一种间接测量法，获取的扭振信号中包含大量的噪声，故而必须采用一定的手段或方法进行降噪。本文采用VMD 算法对原始扭振信号进行分解降噪，并利用PSO 算法搜寻VMD 算法最优参数组合，由此提出基于PSO-VMD 的扭振信号处理方法，具体实现步骤如下:

1) 初始化PSO 算法的相关参数。PSO 算法设定的各项参数如表1 所示。

表1 PSO 各项参数Table 1 PSO parameters

种群数量m 反映了计算时需要的粒子的数目，m 过小，PSO 计算速度快但易于过早收敛，过大，寻优效率降低，通常设置为［10 -100］，Nmax为算法最大迭代次数。

种群维度D 一般用于反映优化的参数个数，本文主要优化VMD 算法的分解个数K 和惩罚因子α两个参数，故而设置为2。

学习因子c1和c2反映了粒子间的学习能力，c1表示自我经验、c2表示种群经验。一般c1和c2取固定常数，并且取c1和c2相等，早期的研究中通常将取值规定为2［19-21］。

惯性权重可调节PSO 算法局部和全局搜索能力，Shi 发现，当w 在0.9～0.4 线性变化时PSO 算法优化能力更好，即采用线性递减策略:

2) PSO 搜寻VMD 算法的参数组合。以VMD算法中的分解个数K 和惩罚因子α 目标函数，以能量熵为适应度函数进行优化，得到最优参数组合［Kopt，αopt］。

3) 将最优参数组合［Kopt，αopt］重新代入到VMD 算法中完成扭振信号的分解，得到Kopt个IMF分量;

4) 计算各IMF 与原始扭振信号的相关系数rK，并取相关系数rK最大(或较大) 对应的IMF 进行扭振信号的重构;

相关系数用来描述经VMD 后得到的各IMF 与原始扭振信号的关联程度，通过计算各IMF 与原始信号自相关系数将其归一化处理［23］，其表达式为

式中: N0为扭振信号y(t) 对应的原始信号个数;为第k 个IMF 的自相关系数;Ry(k) 为扭振信号y(t) 的自相关系数。rK越大表示第K 个IMF与原始信号的相关性越大，含有的转频信息也越丰富。

5) 将重构后的扭振信号进行零点插值，提取扭振瞬时转速波动，最后对扭振瞬时转速波动进行频谱分析，得到扭振瞬时频谱特征。

以上扭振信号处理流程如图3 所示。

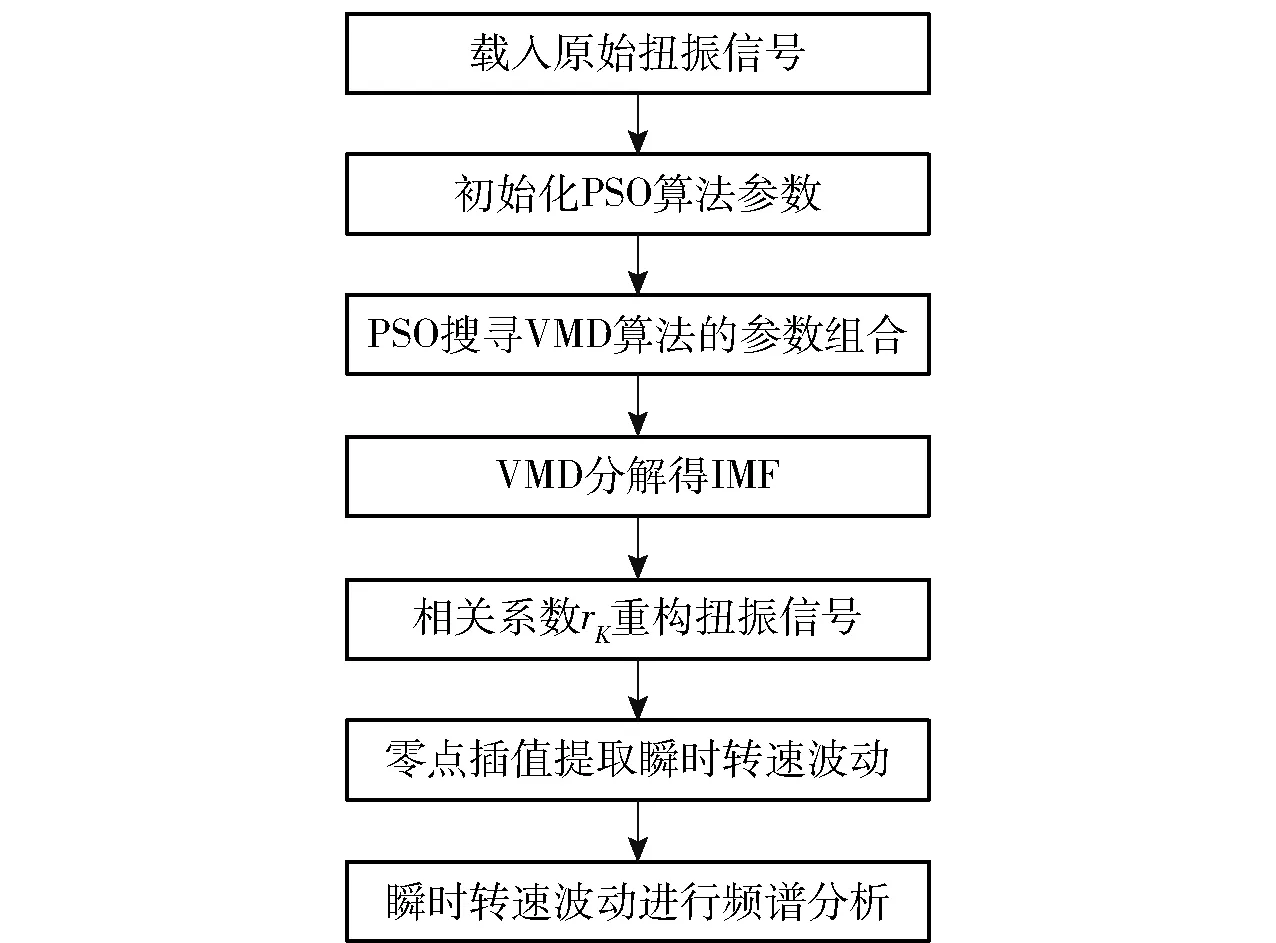
图3 算法流程图Fig.3 Flow chart of the algorithm

4 实验分析

为了验证所提方法的有效性，搭建如图4 所示的扭振频率可调的扭振实验样机进行实验。现场测试中采用加工有100 齿的等分齿轮，安装在实验样机的合适位置(见图4(b))，美国Lion 公司的CPL290 电容式位移传感器采集扭振数据。通过亿恒8 通道ECON MI-7008 数据采集仪记录，采样频率为20 480 Hz，采样时间为2 s，设定实验台转速为600 r/min、扭振频率为50 Hz。采集的扭振信号时域波形如图5 所示。

图4 扭振实验样机Fig.4 Torsional vibration experimental prototype

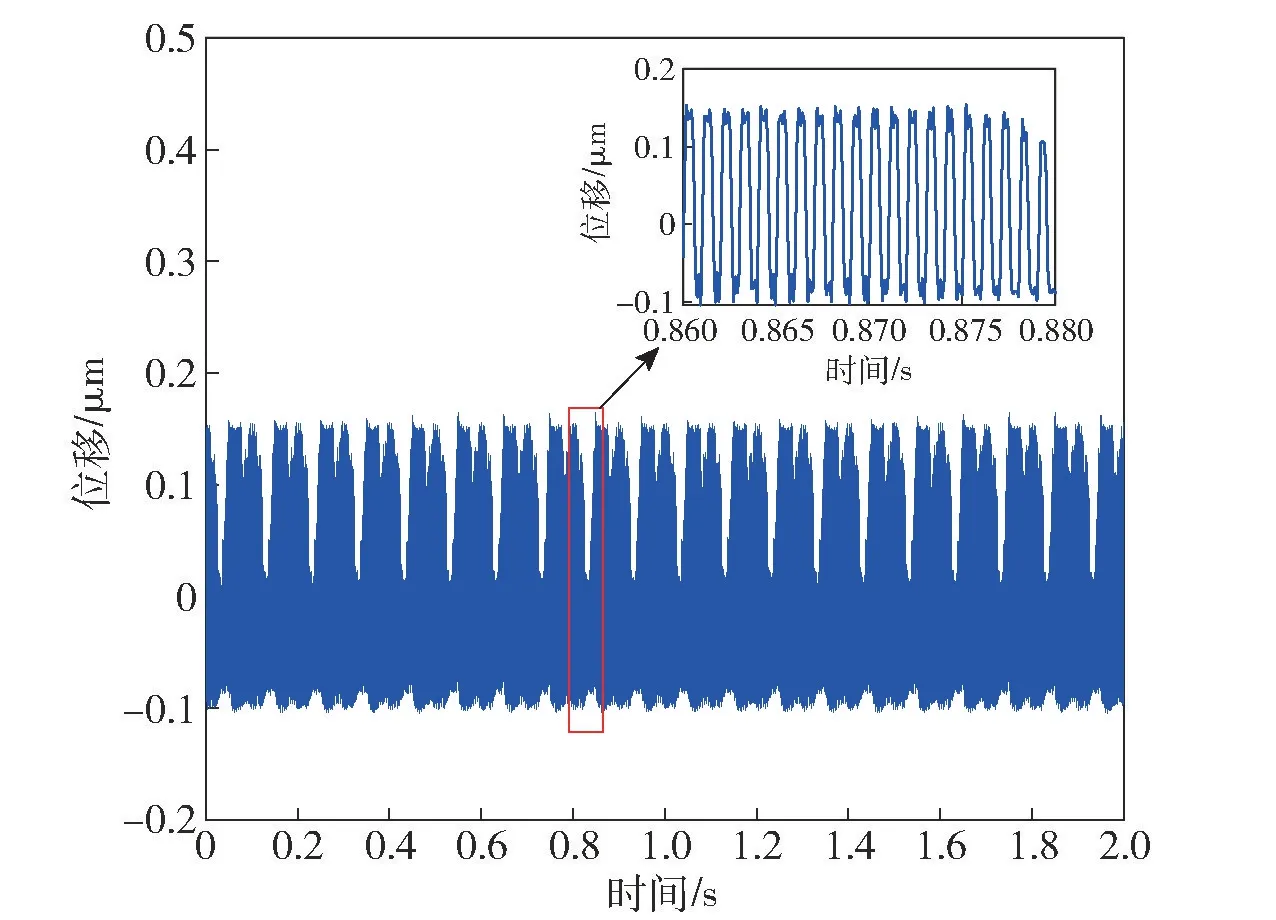
图5 扭振信号时域图Fig.5 Time domain diagram of torsional vibration signals

如图5 所示为扭振试验样机转速为600 r/min、扭振频率为50 Hz 的扭振信号时域波形图以及扭振信号的局部放大图。从时域图中可明显观察到采集到的等分齿轮上信号具有很强的周期性，经过计算每一个周期内共有100 个脉冲信号(类正弦信号)，对应等分齿轮的齿数，说明采集到的扭振信号是正确的。

图6 为扭振信号的频谱分析，从频谱的低频部分可得到扭振转速600 r/min 的转频10 Hz，从高频部分可得到等分齿轮齿的通过频率1 000 Hz，且存在10 Hz 的边频带，从而说明采集的扭振数据的正确性。但是从频谱图中无法得知50 Hz 的来源，说明采用简单的频谱分析并不能有效提取出扭振频率。

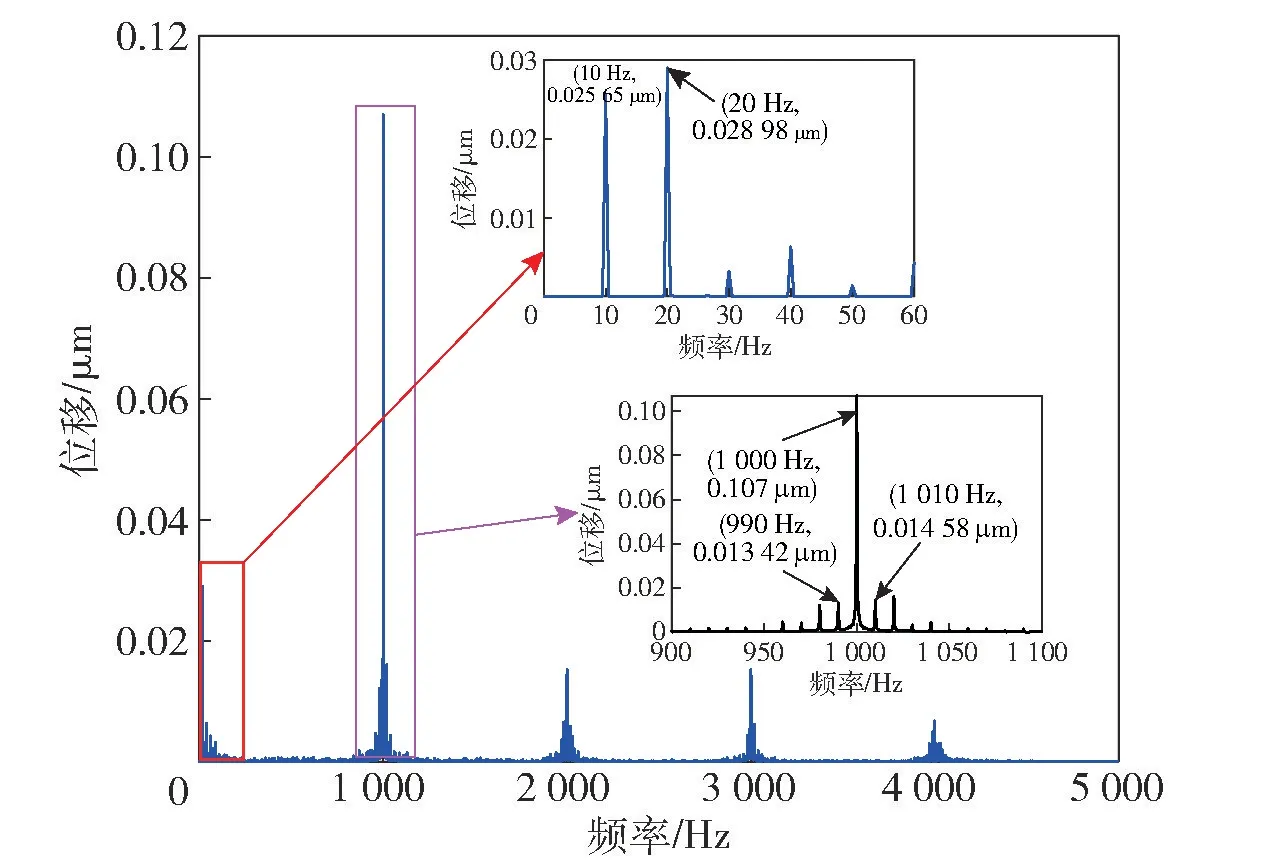
图6 扭振信号频谱分析图Fig.6 Spectrum analysis of torsional vibration signals

采用PSO 优化VMD 参数，得到如图7 所示的适应度函数变化曲线，从图7 中可得，PSO 迭代1 000 次，粒子群适应度函数值最后达到了收敛，完成收敛时粒子群的迭代次数为331，对应VMD 参数组合为［K，α］=［5，300］，将优化得到的最优参数代入VMD 中对扭振信号进行分解，得到5 个单分量IMF，如图8 所示。

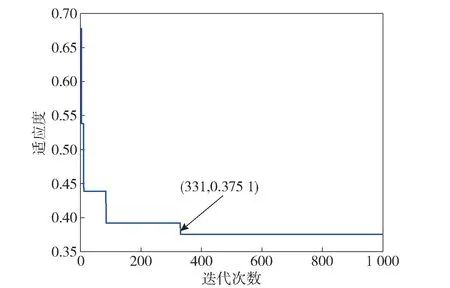
图7 适应度函数曲线Fig.7 Curve of fitness function

从图8 中可以发现经过参数优化后的VMD 能够将扭振信号完全分离。

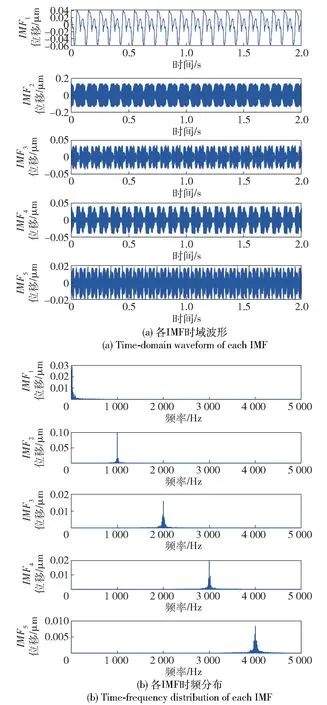
图8 VMD 各IMFFig.8 Decomposition of each IMF by VMD

计算VMD 的5 个IMF 与扭振信号的相关系数rK，结果如表2 所示，选择相关系数最大的IMF2重构扭振信号，IMF2时域图和频谱分析如图9 所示。从图9 中可以得到等分齿轮的工频以及以转轴转频10 Hz 的边频带。对重构的位移信号采用式(6) 的零点插值法求取单齿经过的时间间隔，并用式(7)求解瞬时转速，进而利用式(5) 求解得到如图10 所示的瞬时转速波动数据。对瞬时转速波动信号做频谱分析得到如图11 所示的转速波动频率即为扭振频率。

图9 IMF2时域波形及频谱Fig.9 IMF2 Time domain waveform and spectrum

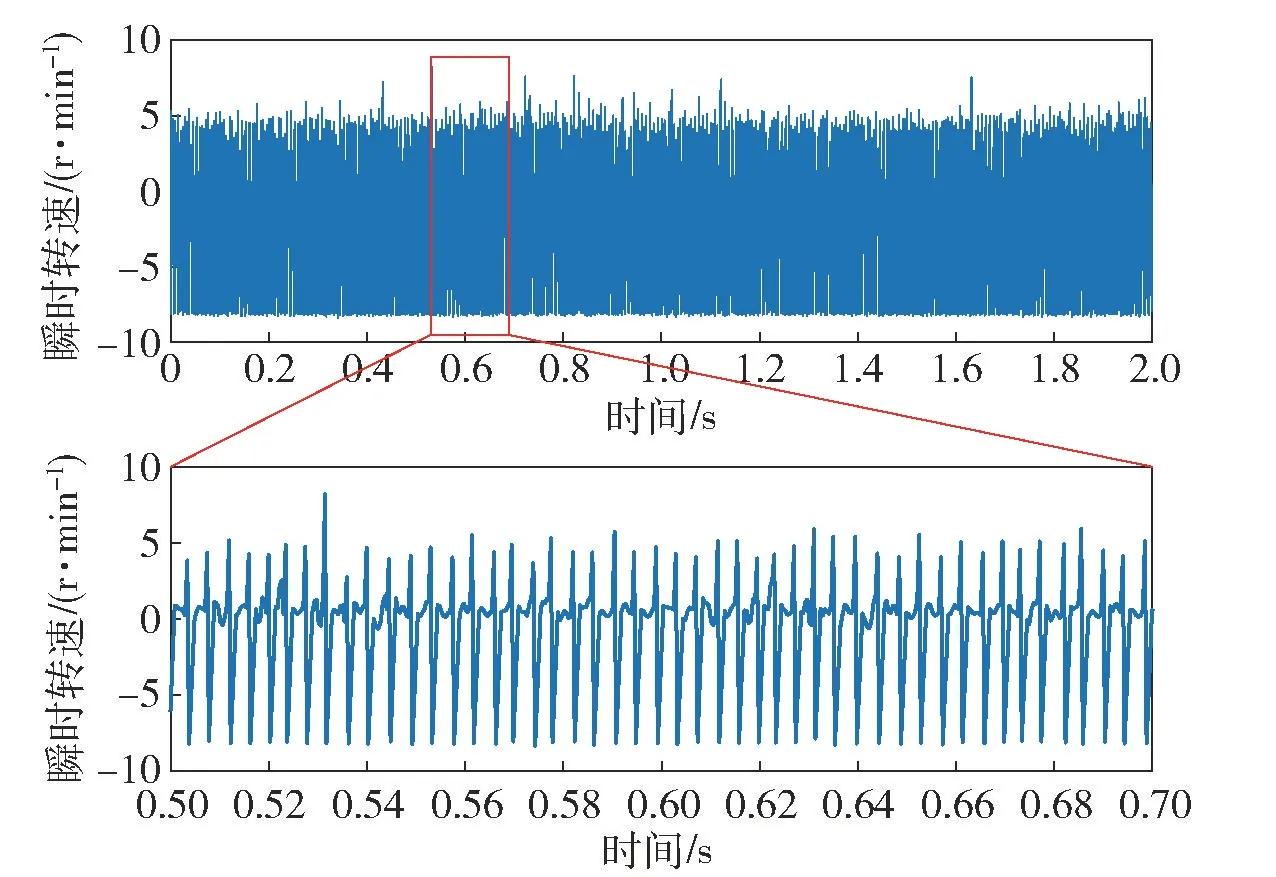
图10 瞬时转速波动Fig.10 Instantaneous speed fluctuation

表2 各IMF 分量相关系数Table 2 Correlation coefficients of IMF components

从图11 频谱分析局部放大图中可以清楚地看到50.02 Hz 的扭振频率及其倍频，同时在扭振倍频两侧存在10 Hz 的边频带，从而证明所提算法能够实现对扭振信号频率的提取，且在考虑频谱分辨率的情况下可以认为扭振提取误差应小于1%。

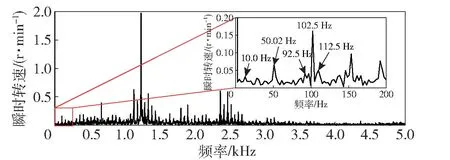
图11 瞬时转速波动的频谱分析Fig.11 Spectrum analysis of instantaneous speed fluctuation

为了进一步验证本算法的优越性，现对未经优化的扭振信号和经集合经验模态分解(EEMD) 分解［24］的扭振信号进行分析，分析结果分别如图12和图13 所示。

从图12(a) 可看出扭振瞬时转速波动信号毫无规律，从图12(b) 扭振瞬时转速波动信号的频谱局部放大可看出，在频谱图中并未找到转轴转频10 Hz分量，虽然找到了50.02 Hz 成分，但是在其二倍频处并未找到以10 Hz 为间隔的边频带，并不能说明此50.05 Hz 是否就是所要寻找的扭振瞬时频率特征。

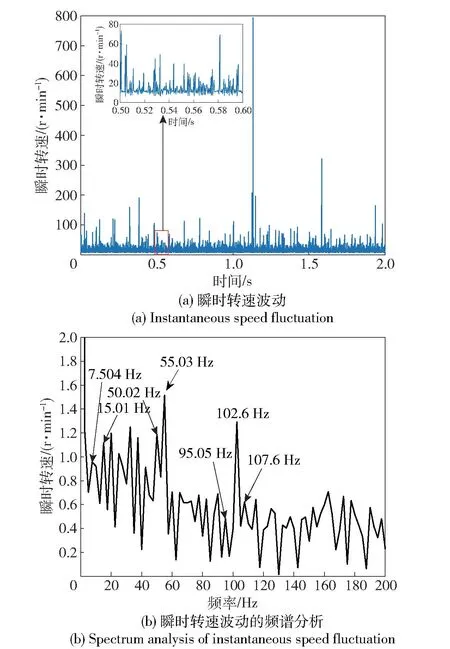
图12 未经优化的扭振信号分析结果Fig.12 Results of unoptimized torsional vibration signals

采用EEMD 对扭振信号进行分解，经过分解发现，前5 个IMF 基本能反映扭振信号的模态，而后求解前5 个IMF 与原始信号的相关系数，选择相关系数最大的IMF2重构扭振信号。

从图13(d) 扭振瞬时转速波动信号的频谱局部放大可看出，在频谱图中虽然找到了50.024 4 Hz 的扭振频率，但是并未找到转轴转频10 Hz 分量，同时也无法找到扭振频率的倍频及以10 Hz 为边频带的成分，从而证明了所提的算法的分解效果更佳。同时又分别对经VMD 分解得到的其他IMF 进行了同样的分析，经过分析发现均无法得到扭振频率特征，充分证明了选择IMF2进行分析的合理性，同时进一步验证了所提算法的有效性。而对于各瞬时转速波动图中所产生的突变成分可能是由于被测转轴质量的不平衡或传感器不严格对中所导致，将在后续的工作中作进一步分析。

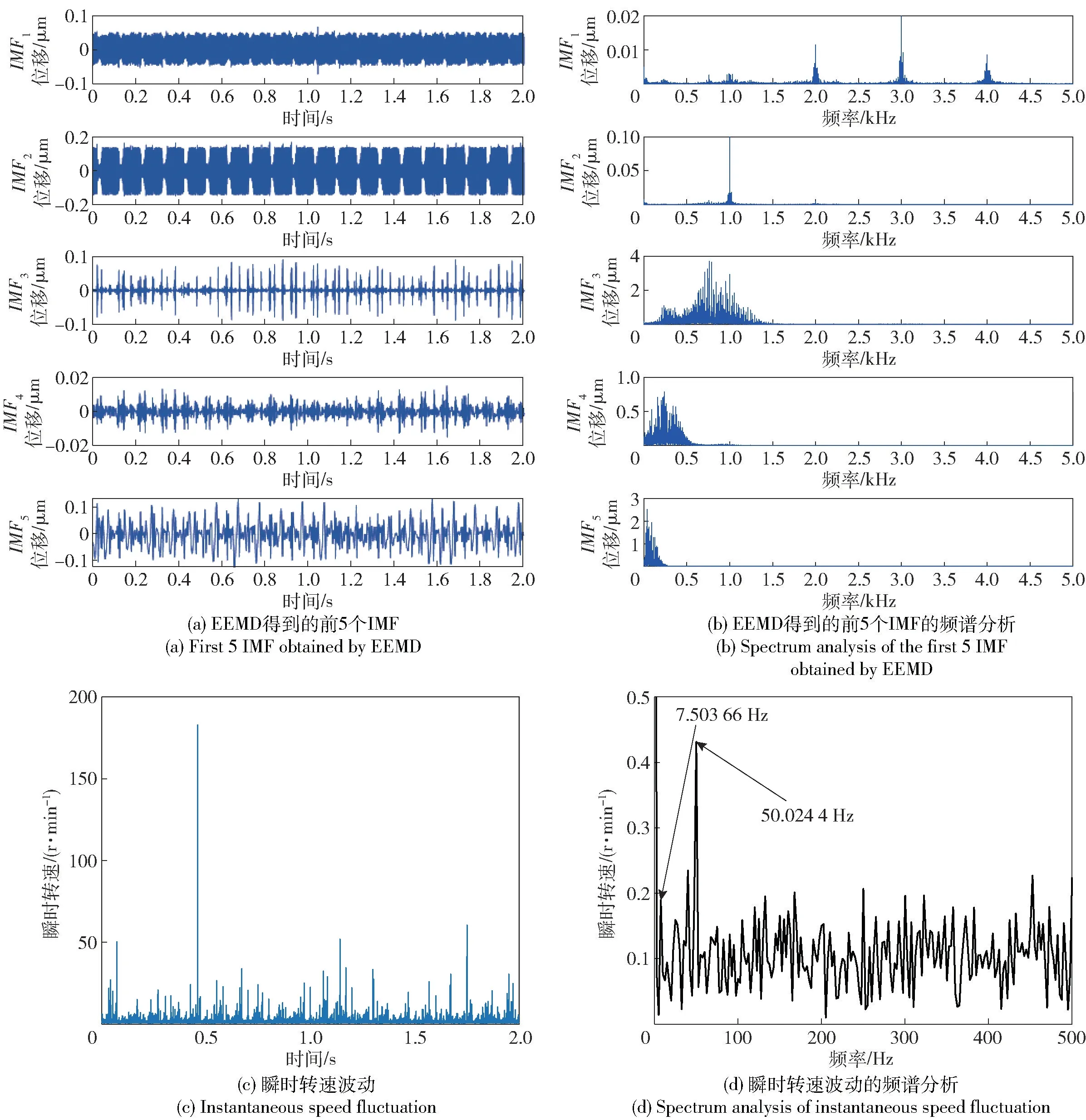
图13 经EEMD 的扭振信号分析结果Fig.13 Analysis results of torsional vibration signal decomposed by EEMD

5 结论

本文提出了一种使用粒子群参数优化的VMD和零点线性插值法的扭振特征频率提取方法。得出主要结论如下:

1) 所提的方法关键在于设置信号能量熵为粒子群参数优化的适应度函数，为VMD 算法提供分解个数 和惩罚因子的最优参数组合。在最优参数组合下，VMD 算法能够准确提取原信号中转频信息最丰富的分量，因而使所提方法具有独特优越性。

2) 对最优分量信号使用零点线性插值法能够更为准确地还原轴系瞬时转速波动信号，即扭振信号，其频谱能够准确体现扭振特征频率。

3) 惯性载荷扭振实验结果表明: 在转速为600 r/min、扭振激励频率为50 Hz 的条件下，对采样频率为20 480 Hz 的位移信号使用所提方法能精确提取扭振瞬时频率特征，误差小于1%。