深海着陆车路径规划及跟踪控制方法

周球，周悦，孙洪鸣，郭威，吴凯，兰彦军

(1.上海海洋大学 工程学院，上海 201306;2.中国科学院 深海科学与工程研究所，海南 三亚 572000;3.中国科学院大学，北京 100049)

0 引言

深海作为人类亟待探索的重要资源宝库，蕴藏着丰富的生物资源和化学能源，尤其是研究生活在深海热液和冷泉区的噬压、噬氧以及化能合成微生物等特殊的生命现象，对探索地球地质演化和生命起源具有重要的意义［1-2］。深海着陆车(DSLV) 作为一种将履带底盘与传统水下机器人相结合的新型水下装备，具备大范围移动考察、定点精细化和长周期自主作业的能力［2］，可完成对海底资源的自主探测。

DSLV 要求在自携带能源有限条件下实现长距离作业，为此需要规划较短参考路径以节省能耗、提高作业范围。同时，为实时、高效跟踪规划的路径，需要采用合适的跟踪算法。模型预测控制(MPC)算法由于可以根据车辆当前状态量信息计算得到预测时域内的状态量信息、实现对目标函数的在线滚动优化等优点，逐步引起学术界重视［3-5］。文献［6］基于轮胎非线性特性影响，提出考虑轮胎侧向力计算误差的自适应MPC 算法，提高了未知工况下路径跟踪控制的性能;文献［7］综合考虑动静态障碍物和人类驾驶行为，提出了一种用于车辆轨迹跟踪控制的线性时变MPC 控制方案，提高了路径跟踪控制的稳定性;文献［8］基于级联控制策略和MPC 算法设计了自主水下航行器(AUV) 控制器，减少了路径跟踪时舵角饱和现象;文献［9］结合经验公式和和神经网络算法调整MPC 的预瞄步数和步长，降低了跟踪误差。上述方案均在不同方面提高了路径跟踪的性能，但未考虑到目标函数中固定的权重矩阵无法同时兼顾稳定性和跟踪精度，难以在跟踪误差不断变化的情况下取得最佳跟踪效果。

根据海底具体环境，本文提出一种变参数蚁群优化(VACO) 算法和根据跟踪距离误差进行自适应权重调节的模型预测控制(AWMPC) 算法，进行DSLV 自主路径规划与跟踪，降低了规划路径长度，提高了路径跟踪的精度。

1 DSLV 运动学模型

本文研制的DSLV 采用双电机后驱方式，通过差动方式控制DSLV 前进、后退、转向运动。双侧电机驱动示意图如图1 所示。

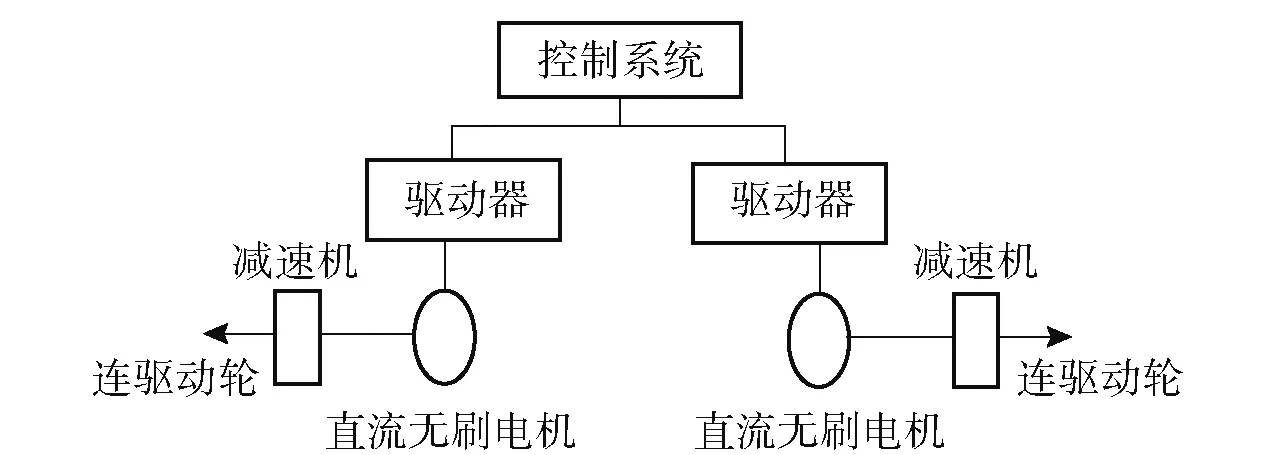
图1 双侧电机驱动示意图Fig.1 Schematic diagram of the dual motor drive

在笛卡尔坐标系OXYZ 下，令xc、yc分别为DSLV 几何中心点的横坐标和纵坐标，φ 为方向角，vl和vr分别为左右履带线速度，v 为爬行速度，d 为左右履带的中心距，D 为车身宽度，rd为驱动轮半径，rl和rr为左右履带瞬时转向半径，oc为瞬心，ω 为转向角速度。其差速运动示意图如图2 所示。

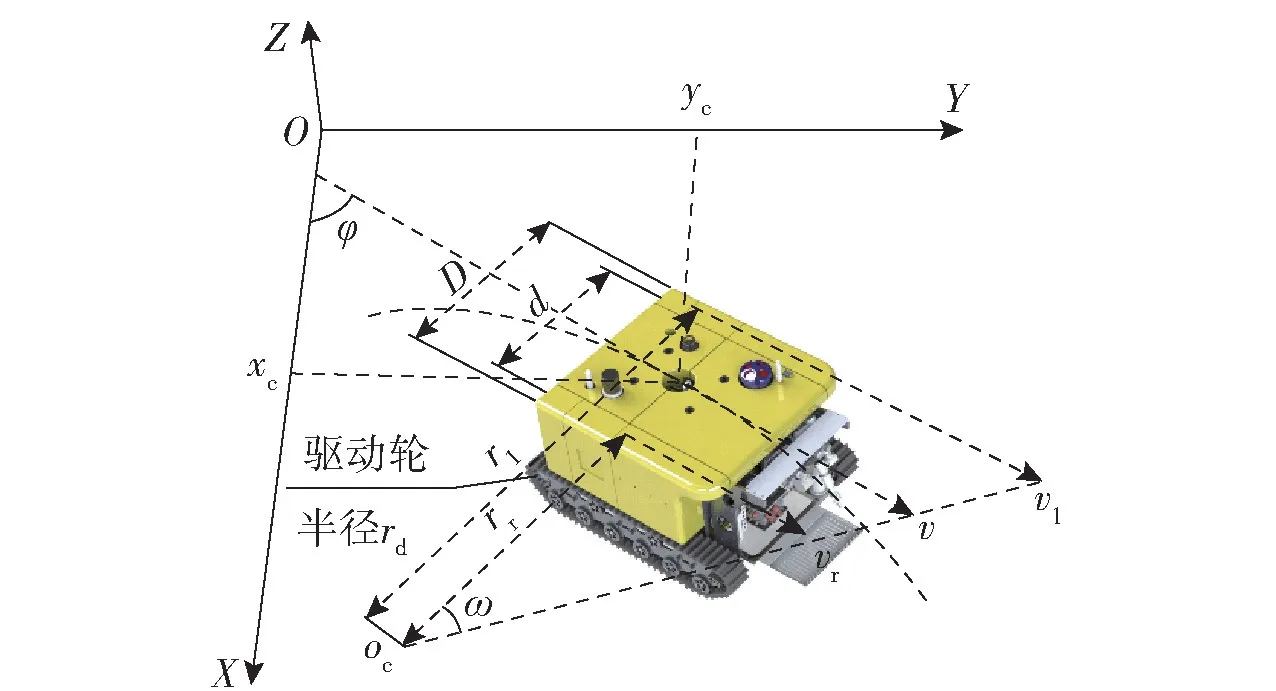
图2 DSLV 差速运动示意图Fig.2 Diagram of DSLV differential motion

据“深海勇士”号和“奋斗者”号载人潜水器的作业经验，较平坦的深海海底主要分为沙质底和泥质底两种，除马里亚纳海沟外，其他海域这两种底质潜水器沉降不大。项目组设计的DSLV 在海底的负浮力质量约为50 kg，为应对DSLV 着底时受到的冲击力，对履带结构的张紧轮支架进行了改进［10］。为此，DSLV 选择在较为平坦的沙质底作业，且爬行速度较慢(约为0.5 m/s)，忽略Z 轴方向的运动，并假设DSLV 质心与几何中心重合［11］，则由图2 可得

式中:vx和vy分别为DSLV 在x 轴和y 轴的速度分量;sl、sr分别为DSLV 左右两侧履带的滑转率;ωl和ωr分别为DSLV 左右两侧驱动轮角速度。

DSLV 在做转向运动时，由于左右履带的瞬心相同，瞬时圆周运动的角速度ω 相同，旋转半径不同，则d 可表示为

进而可得

选取状态量ξ=［xcycφ］T，控制量u=［v ω］T，构建其运动学模型为

其一般形式可表示为

2 DSLV 路径规划与跟踪控制

DSLV 路径规划与跟踪控制是根据海底信息，在两个作业点之间采用VACO 算法规划出符合行驶条件的最短路径，经过4 阶B 样条曲线平滑后作为参考路径;将实际状态量ξ 与参考状态量ξr输入到AWMPC 控制器中，并根据跟踪距离误差E 的大小对目标函数的控制量误差增量权重矩阵R 进行自适应调整，通过求解目标函数得出最优控制序列ΔU*，并将第一个时刻的控制增量输入AWMPC 控制器中［12］。通过实时控制DSLV 的爬行速度和角速度，使之平稳、安全的跟踪规划的路径。系统总体设计框架如图3 所示。

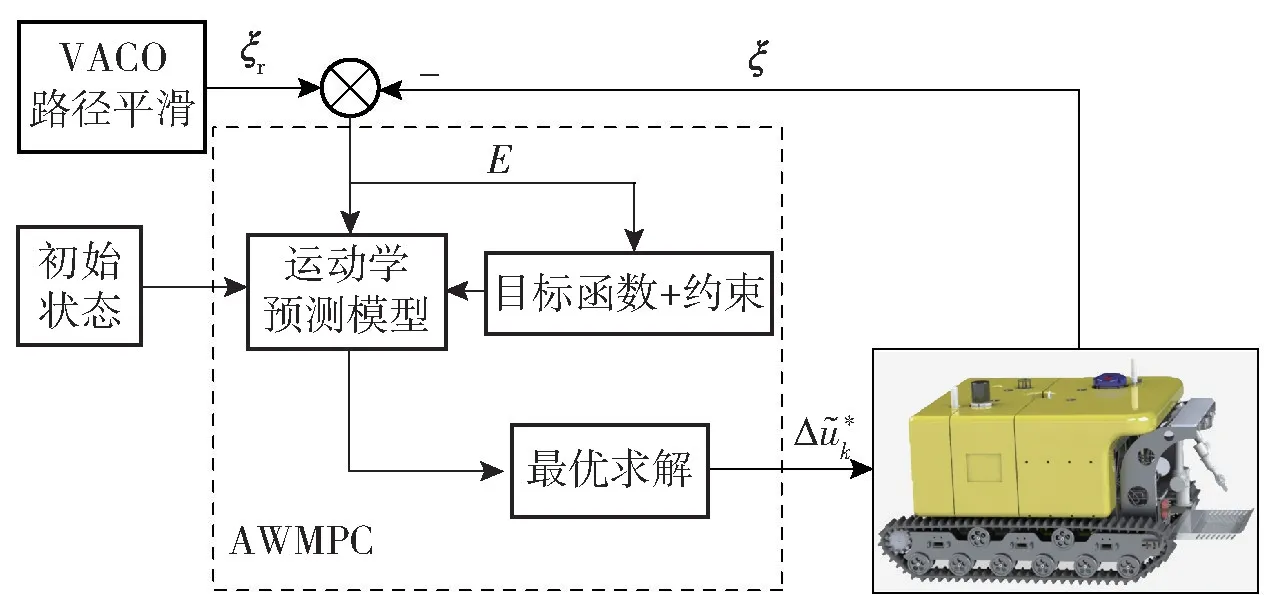
图3 VACO-AWMPC 总体设计框架Fig.3 Overall design framework of VACO-AWMPC

2.1 VACO 路径规划

蚁群优化(ACO)算法具有鲁棒性强和分布式计算的特点［13-14］，在进行路径规划时，蚂蚁∂在t 时刻从点i 转移到点j 的概率为

式中: ∂={1，2，3，…，σ}，σ 为蚁群数量;τij(t) 表示蚂蚁在t 时刻从点i 到点j 路径上残留的信息素浓度;μij(t)=1/dij为启发函数，表示蚂蚁从点i 到点j的期望程度，dij为点i 到点j 的距离;α 为残留信息素的重要程度;β 为启发函数的重要程度;Ω∂为蚂蚁∂在t 时刻从点i 允许到达点的集合。考虑到μij(t)的取值使得ACO 在路径规划时转移概率差异不大，在寻优过程中需要较多次迭代，本文将启发函数μij(t) 的取值修改为(1/dij)2，增大不同步长的信息素差异，以提高ACO 的寻优效率。

信息素更新公式如下:

式中:ρ 为挥发因子，取(0，1) 之间的常数;Δτij表示本次迭代中所有蚂蚁在点i 到点j 路径上释放的信息素浓度之和;表示蚂蚁∂在点i 到点j 的路径上释放的信息素浓度;G 为信息素增加强度系数;L∂为本次循环中蚂蚁∂走过的路径总长度。

由于信息素挥发因子ρ 的大小决定了蚁群在寻找最短路径的过程中信息素挥发的快慢程度，针对ACO 中ρ 恒定，无法兼顾收敛速度和易陷入局部最优解的问题，本文提出将反正切函数进行平移、伸缩和翻转变换后替代ACO 中的恒值ρ。由于反正切函数经过翻转后随自变量的增加而减小。在算法迭代次初期，ρ 较大，前面蚂蚁留下的信息素会很快挥发，后续蚂蚁受到前面蚂蚁留下信息素的影响较小，会以更高的概率选择未走过的路径，能够扩大搜索范围，降低陷入局部最短路径的概率。在算法迭代后期，ρ 较小，前面蚂蚁留下的信息素挥发较慢，后续蚂蚁受到前面蚂蚁留下信息素的影响较大，使得算法以更快的速度收敛，减少找到最短路径所需的迭代次数，VACO 中挥发因子ρ 为

式中: e 为纵坐标平移系数;a 为纵坐标放大倍数;ζ 为迭代次数;b 为横坐标平移系数;c 为横坐标缩放比例。VACO 中ρ 的值能够随着ζ 的变化进行动态调整，使得算法能够较快收敛且不易陷入局部最优。

路径规划与路径长度、所需时间、可行性、及安全性等多种因素有关。由于深海着陆车在海底作业时自身携带能源有限，需要在安全的前提下重点考虑降低规划路径的长度以节省能耗，而安全性通过与障碍间预留安全距离来保证，其他因素不做考虑。为获取最短路径，设路径规划目标函数为

式中:Lz为第z 次迭代的最短路径长度，Lz=min L∂，其中为目标点，MO为规划路径的起始点;γ 为算法迭代次数。

2.2 MPC 算法

MPC 是将DSLV 的运动学模型经过线性化、离散化后递推得到预测模型，然后在k 时刻通过求解带约束条件的目标函数得到最优控制序列ΔU*，并将控制序列的第一个控制增量输入控制器中，然后至k+1 时刻，重复上述过程，滚动完成路径跟踪过程［15-16］，MPC 路径跟踪控制示意图如图4 所示。图4 中: 令Np为预测时域，Nc为控制时域(Np≥Nc)，ξmax和ξmin为状态量约束为控制增量约束。

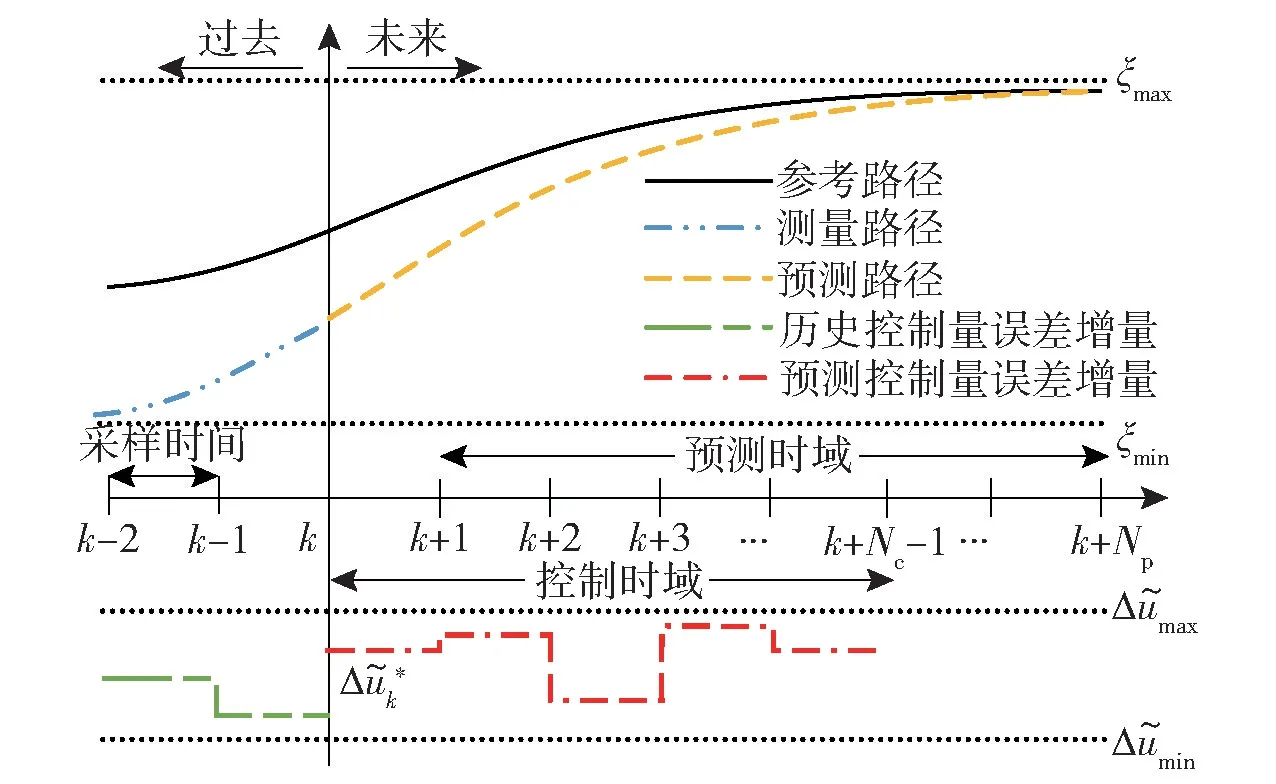
图4 MPC 路径跟踪示意图Fig.4 Schematic diagram of MPC path tracking

2.2.1 非线性模型线性化

由式(2) 可知，DSLV 运动学模型是一个典型的非线性系统，考虑到线性模型具有易于求解、计算速度快等优点［17-18］，将式(3) 进行线性化，使用Taylor公式将式(3) 在VACO 规划的参考路径上某点r 处进行1 阶Taylor 展开并忽略高阶项［19-20］，可得

2.2.2 离散化

采用Forward Euler 方法对式(11) 进行离散化，设采样时间为T，则式(11) 可表示为

由式(12) 移项可得离散化线性时变模型为

为了使DSLV 平稳运行，需对控制量误差增量进行约束，为此引入控制量误差增量，构建增广状态量如下:

则由式(13)、式(14) 得

2.2.3 预测模型

令Np为预测时域，Nc为控制时域(Np≥Nc)，则预测时域内的状态量误差为

2.2.4 目标函数

本文建立的跟踪目标函数为

式中:第1 项为状态误差，表示路径跟踪能力，其中Q1为状态误差加权矩阵为单个状态误差加权矩阵;第2 项为输出控制增量，表示系统的能量消耗，其中R1为控制增量加权矩阵，R1=R⊗为单个控制增量加权矩阵。

考虑到两个权重参数的相对性，为简化起见，本文取Q1为固定参数的主对角线矩阵。考虑到恒定矩阵R 无法兼顾不同跟踪距离误差情况下的跟踪性能，本文提出根据跟踪距离误差对R 进行自适应调节，即当跟踪距离误差E 小于阈值L 时，R 能够随着E 增大而增大;否则，若初始时刻DSLV 不在规划路径上，则此时E 会比较大，将会使R 很大，可能造成系统难以收敛，跟踪失效。为此，根据系统控制输出能力和提高稳定性的需求，对R 进行限幅，即当E大于设定阈值L 时，将其设为一个固定值。R 调节公式如下:

式中:a1、b1、L 均为常数;e 为自然常数。

为便于计算机求解，将式(18) 变换为如下二次规划问题:

式中:H=ΘTQ1Θ+R1;g=ETQ1Θ，E=ψh(k) 。

对于控制量误差及其增量，有如下递推式:

考虑到DSLV 由左右两侧电机通过驱动轮带动履带进行运动，在设计跟踪目标函数时为防止控制量剧烈变化引起系统的机械冲击以及跟踪过程中偏离参考控制量［21］，为此加入控制量误差增量约束和控制量误差约束。设控制量误差增量约束的上下限分别为ΔUmax和ΔUmin，控制量误差约束的上下限分别为Umax和Umin，控制量和控制增量约束分别为同理。

2.2.5 反馈机制

根据式(20) 进行求解后，得到如下控制增量序列:

在每一个控制周期内，实时获取参考路径与DSLV 状态量信息，然后重复上述过程，实现对规划路径的有效跟踪。

3 算法仿真与分析

DSLV 在复杂海底通过定制的深海相机和MD750D 前视声纳系统获得海底环境信息，并借助定制的深海电机驱动履带进行差速运动，然后通过Evologics 超短基线结合Waterlink A50 型多普勒和电机配备的模拟霍尔传感器计算自己的位置信息和速度，基于美国霍尼韦尔公司生产的HMR3200 型电子罗盘获取方向角信息，结合VACO-AWMPC 算法完成路径规划与跟踪。

在路径跟踪时，采用栅格图法构建海底环境的二维简化模型。为便于计算将DSLV 视作质点，考虑到DSLV 容易因自身体积与障碍物发生碰撞，为此根据DSLV 物理尺寸与预留安全距离之和来膨胀障碍物［22］，即障碍物膨胀增量为DSLV 车身宽度一半与安全距离之和，以简化路径规划时的计算量。

为验证VACO 的有效性，将ACO 的寻优效果作为对照组，在含有静态障碍物30 m ×30 m 区域进行仿真实验，设置路径规划的起始坐标点为Mo(0.5，29.5)，目标坐标点为Me(29.5，0.5)，预留安全距离为1 m，取G=10，σ=50，α=1，β=7，γ=100，ρ=0.3。VACO 中ρ 的取值和μij(t) 的取值如2.1 节所示，其中参数a、b、c、e 取值分别为0.15、30、10、0.5，其余同ACO。某次路径规划试验结果对比如图5 所示，为不失一般性，分别对ACO 与VACO 进行30 次仿真实验，实验结果的平均值如表1 所示。

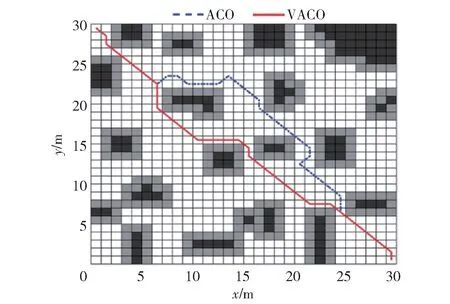
图5 路径规划结果对比Fig.5 Comparison of path planning results

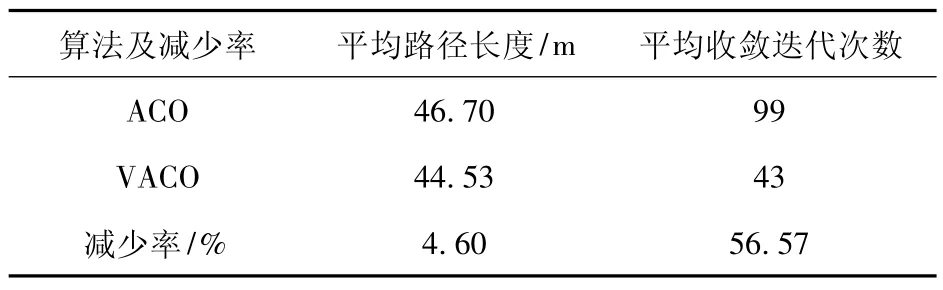
表1 仿真实验结果平均值对比Table 1 Comparison of mean values of simulation results

由图5 与表1 可见，采用VACO 规划的路径长度明显降低，收敛所需的迭代次数更少，路径长度和收敛时迭代次数分别降低4.60%和56.57%。

考虑到VACO 规划的路径在转向处角度较大，不利于DSLV 在路径跟踪过程中的平稳运行，对蚁群算法规划的路径进行4 阶B 样条曲线平滑处理作为参考路径［23］。设平滑后参考路径上某点坐标为(xr，yr)，其下一个采样点坐标为(xr+1，yr+1)，根据公式arctan ［(yr+1-yr)/(xr+1-xr) ］计算参考点(xr，yr) 处的参考方向角。

设给定的 DSLV 初始状态量 ξo=［0m 28 m π/3 m］T，按照平滑处理后的规划路径及参考位置方向角，进行DSLV 跟踪控制。预测模型参数及约束列于表2 中。

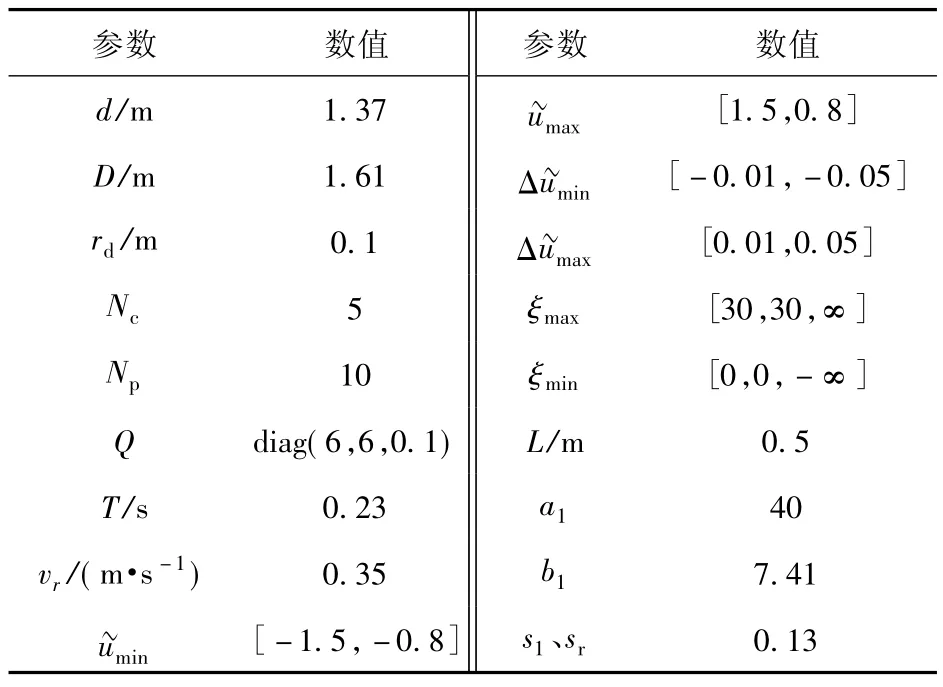
表2 预测模型参数及配置Table 2 Parameters and configuration of the predictive model

当采用MPC 算法时R 为固定矩阵，取8I2×2;当采用AWMPC 算法时自适应权重矩阵R 取值见式(19)，分别对两种情况进行仿真实验。为便于观察，对仿真结果进行了局部放大，路径跟踪仿真实验结果如图6～图10 所示。

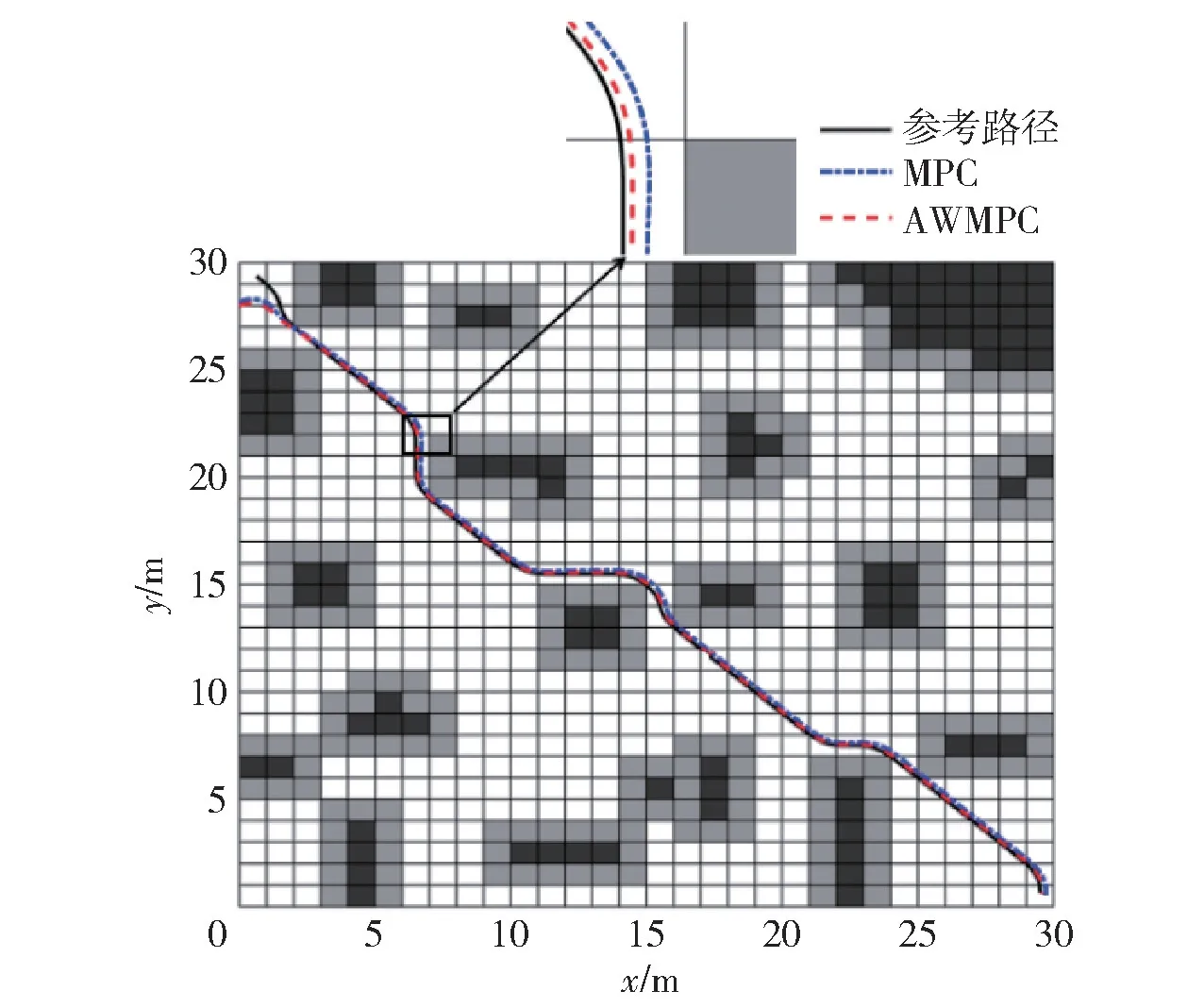
图6 路径跟踪结果对比Fig.6 Comparison of path tracking results

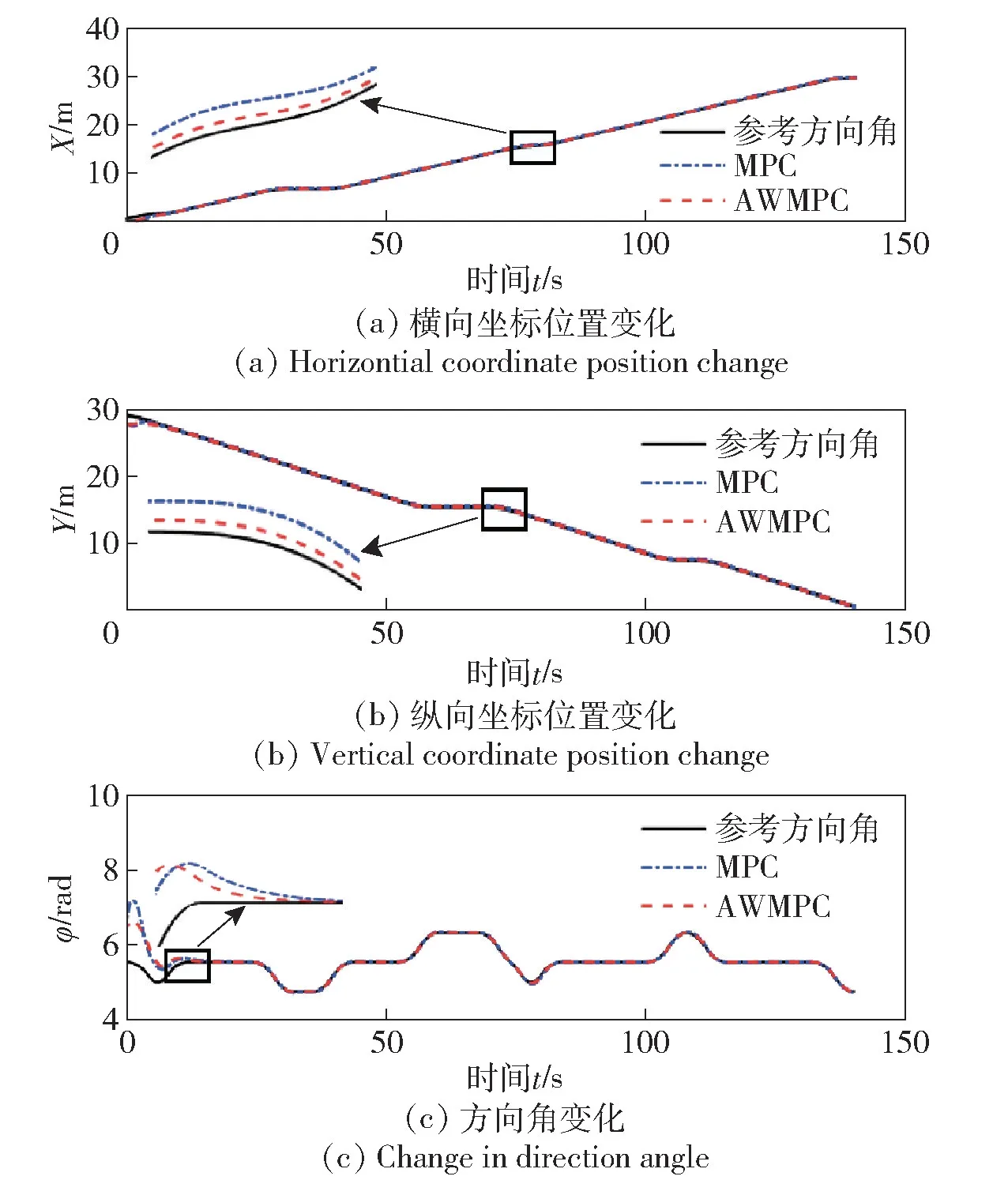
图7 状态量跟踪控制效果对比Fig.7 Comparison of state quantity tracking control effects

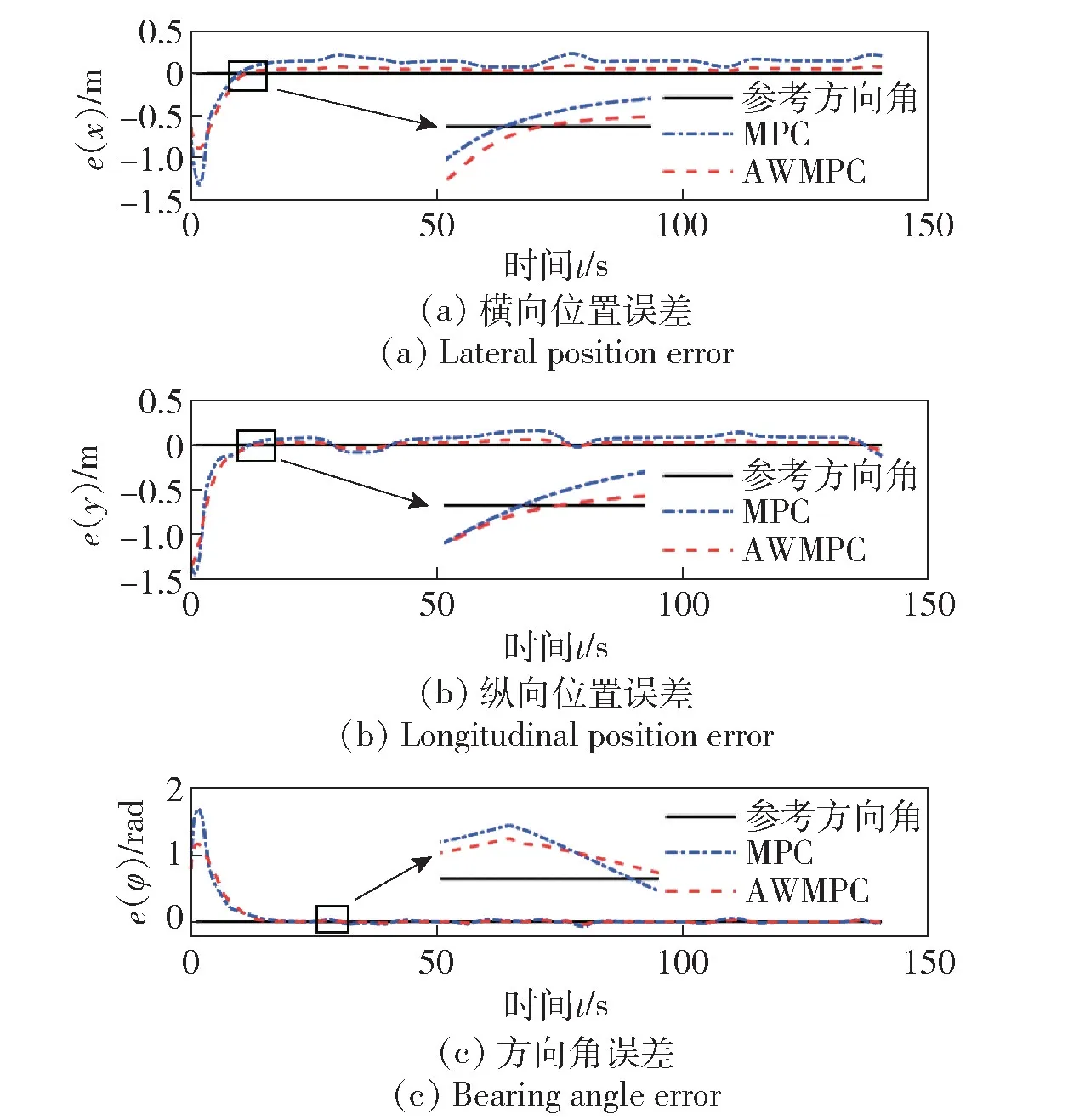
图8 状态量误差变化对比Fig.8 Comparison of state quantity error change

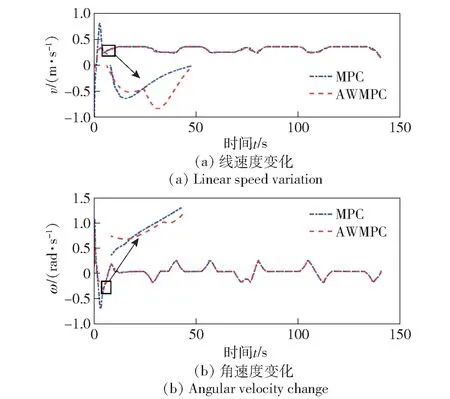
图9 控制量变化效果对比Fig.9 Comparison of control quantity change effect

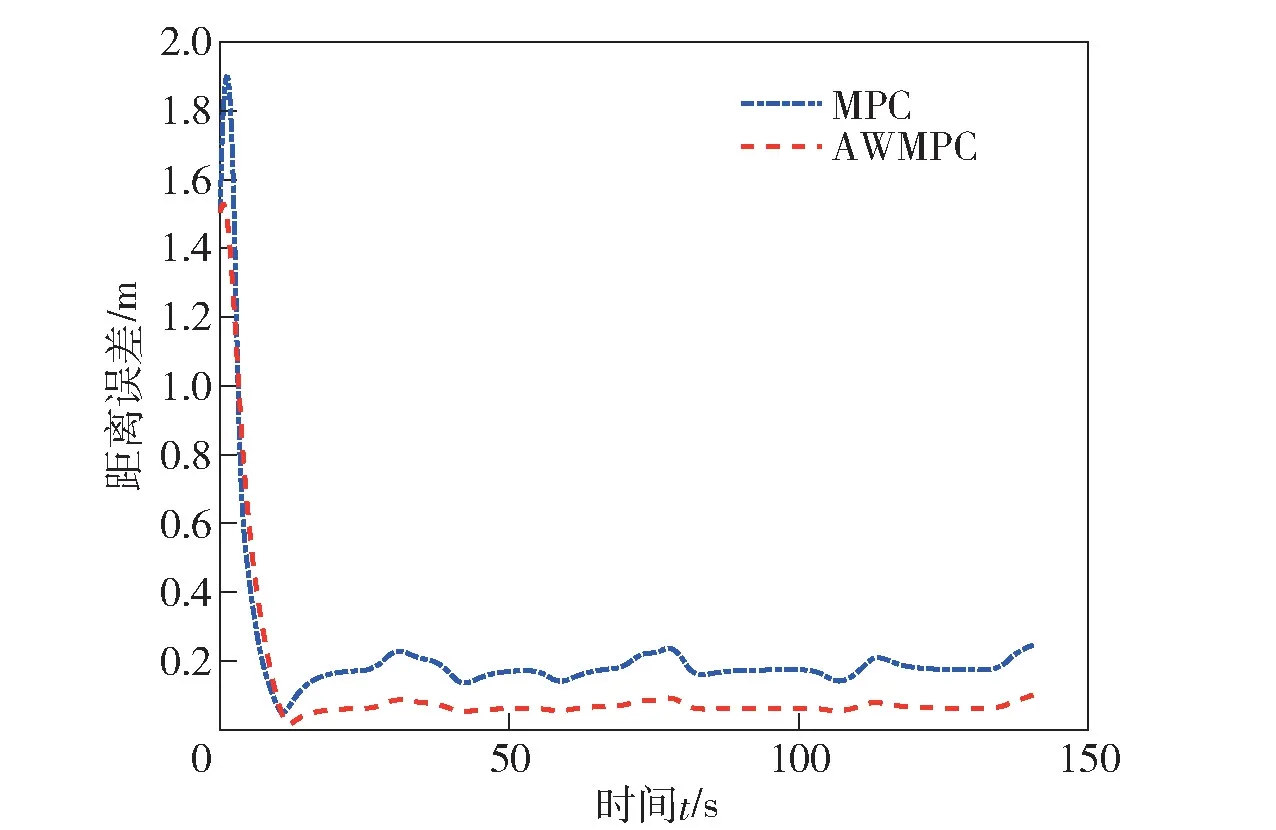
图10 跟踪距离误差对比Fig.10 Comparison of tracking distance error

由图6 可见，起始时刻DSLV 并不在规划路径上，DSLV 开始运行后，逐渐向规划路径靠近，最终都能达到较好的跟踪效果，但采用AWMPC 算法跟踪精度明显更高。

由图7 和图8 可见，采用AWMPC 算法跟踪路径时横向、纵向位置误差以及方向角跟踪误差更小。

由图9 可以看出，DSLV 在转向时速度会出现波动，但完成转向后会迅速恢复稳定，采用AWMPC算法在自适应权重矩阵R 切换初期出现了线速度和角速度波动，但始终保持在可接受范围内。

由图10 可见，采用AWMPC 算法的跟踪距离误差更低。在包含起始位置误差的情况下，两种方式下平均跟踪距离误差分别为0.215 9 m 和0.113 1 m，降低47.6%。

4 结论

本文用反正切函数取代ACO 中信息素挥发因子ρ，同时考虑控制系统约束构建AWMPC 系统，对跟踪目标函数中权重矩阵R 进行自适应调节。并对DSLV 采用VACO 和AWMPC 算法进行路径规划和跟踪效果进行了仿真实验。得出主要结论如下:

1) 通过用反正切函数取代ACO 中信息素挥发因子ρ，使VACO 中的信息素挥发因子能够随着迭代次数的变化进行调整，达到了降低规划路径长度和更快收敛的目的。

2) 通过修改跟踪目标函数中权重矩阵R，使矩阵R 随着跟踪距离误差的变化进行自适应调整，提高了路径跟踪的稳定性和跟踪精度。

3) 通过结合VACO 和AWMPC 算法，使得DSLV 能够在复杂海底环境下安全、高效、自主地进行路径规划及跟踪。

本文的研究方法为DSLV 及相关深海智能装备路径规划与跟踪实现提供了理论支撑。但研究过程中对履带滑转进行了简化处理，后续将考虑采用黑箱建模方法对复杂三维海底环境下的滑转率进行实时估计，提高运动模型的精确性;在路径跟综过程中，仍存在一定的稳态误差，后续工作将针对该部分进行更为深入的研究，进一步完善DSLV 的跟踪控制系统设计。