多轮分布式驱动车辆可重构集成协调控制方法

李斐然，张雨甜，魏超，胡纪滨，吴维

(北京理工大学 机械与车辆学院，北京 100081)

0 引言

随着轮式车辆在军用领域的技术革新与发展，多轮分布式独立电驱动车辆以其优越的机动性、灵活性，在战术车辆中逐步占有重要战略地位［1］，同时要求车辆底盘主动控制系统对驾驶意图具有精确的响应和高效的执行能力。分布式驱动平台是一种典型过驱动系统［2］，其包含的执行器数目一般明显多于被控目标变量数，可重构的控制分配方法对于这一冗余系统的性能提升有着重要意义。其可保证在不同目标优先级及执行器约束下的控制模型和控制律的普遍适用［3］，实现主动执行机构的重新配置，从而充分发挥分布式驱动控制系统的潜质。

随着军用车辆技术中车辆底盘主动执行器及其控制系统的数目与复杂程度的急剧增加，通常学者们采用集成协调控制方法来应对，以降低各控制方法间功能重叠、干涉所带来的不利影响。其中，运动控制器的灵敏度、跟踪精度等更受关注［4］，但较少将轮胎力分配中的复杂可能性集成到总体控制架构。

此外，分布式驱动车辆的驱动力分配方法主要可概括为基于规则的分配、基于优化的分配两大类。文献［5］针对轨迹跟踪问题综合对比了上述方法，结果表明规则分配更简单易行，优化分配更便于优化目标调节。文献［6］采用的基于规则的按比例分配方法，虽然简便易行，但通常无法将执行器的复杂饱和限制考虑在内，故其分配精度不足以满足控制需求。基于优化的求解在引入优化目标的同时，将饱和限制作为约束条件［7］，分配精度可接受但运算量增加。文献［8］采用的二次规划法(QP) 为典型的非线性优化控制方法，虽然能够加快收敛性，但对初始解依赖性较强且实时性差。文献［9］采用KKT条件结合拉格朗日乘子法做优化求解，但这一方法采用离线计算，存在许多应用条件限制。为降低优化问题带来的计算量显著增加，文献［10］采用伪逆法作为典型的线性优化方法进行解算，简便易行，但对于执行器的位置和速率限制考虑不够全面，因而给出的分配值存在无法由实际执行机构产生、分配效率较低的可能。再分配加权伪逆(RWPI) 法在伪逆法基础上，利用矩阵零空间特性对分配结果进行二次调节，综合考虑了分配器饱和约束问题，同时仍可发挥其在计算量、精度及实时性方面的优势，该方法在航空、船舶和机器人等领域的运动平台控制问题上得到了有效应用［11］。

本文引入执行器重构矩阵搭建了多轮分布式驱动特种车辆动力学模型，并在集成协调控制架构中，利用自适应滑模控制器实现广义控制力质心矢量的精准生成，建立质心矢量与车轮子矢量映射模型。又将分配控制凝练为一个考虑主动执行器饱和限制的再分配加权伪逆求解问题，获得每个车轮处的车轮子矢量，最终完成执行指令的解析，并对该控制方法进行了验证。

1 车辆系统动力学可重构模型

本文选取三轴双轨车辆纵向、横向和横摆三种关键运动，建立非线性耦合动力学模型，如图1 所示。

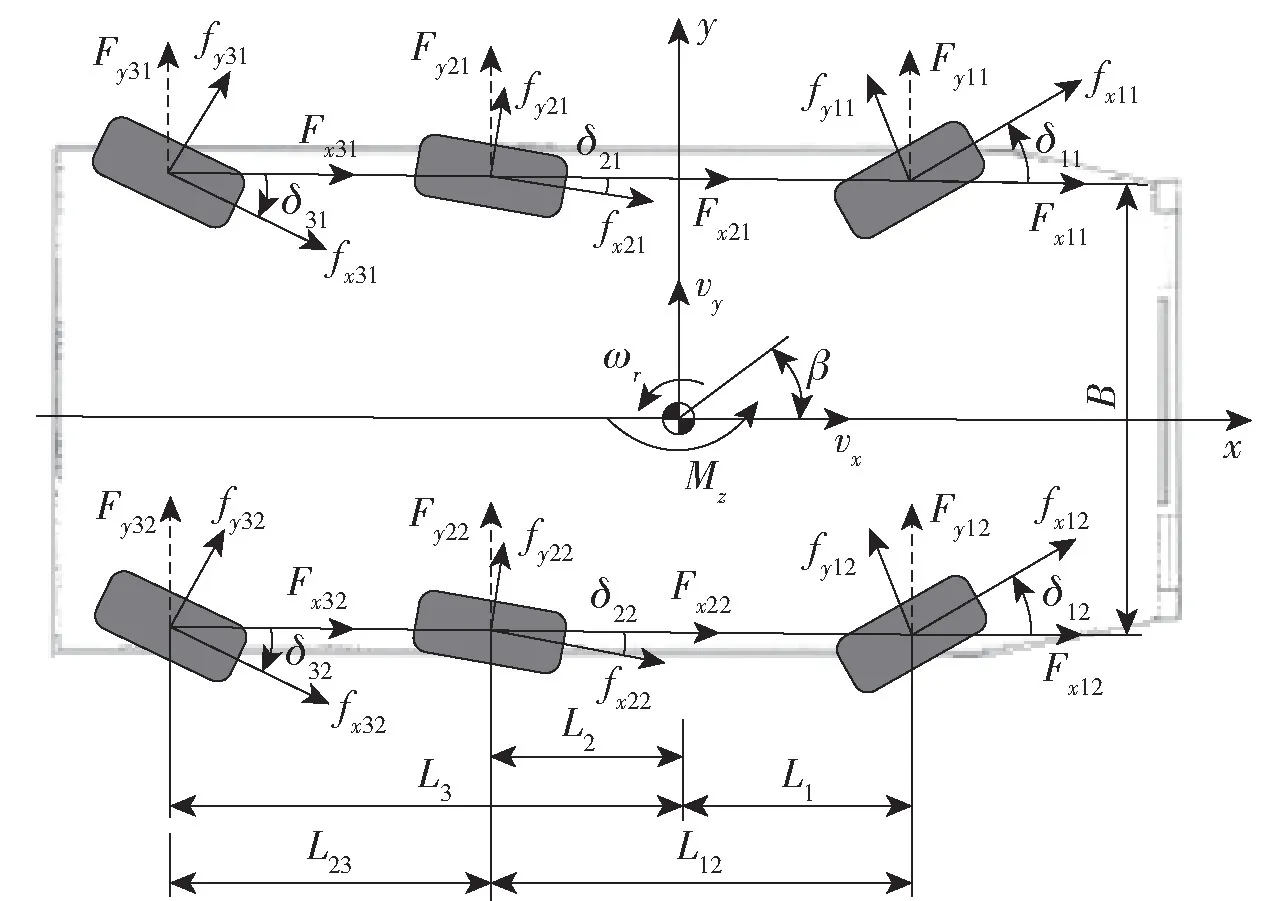
图1 整车动力学模型Fig.1 Dynamic model of the whole vehicle

式中:m 为整车质量;u、v 为纵向、侧向速度;ωz为横摆角速度;Fx为纵向力;Fy为横向力;Mz为横摆力矩。定义广义控制力矢量FCG为质心处广义力和力矩:

定义车轮子矢量(WFV) 为由行驶指令产生的轮胎力fij，以及主动执行机构产生的补偿作用力Δfij的合力，令各车轮子矢量沿x 轴、y 轴分解得到的轮胎力Fxij、Fyij构成子矢量分量矩阵FWij(i 表示轴，j 表示左右侧) 。车轮子矢量与分量之间的映射关系描述如下:

式中:ΓWij为WFV 到子矢量分量的映射矩阵，

δij为各车轮转角;Θij为主动执行器调用矩阵，由布尔因子ϑxij、ϑyij组成，决定第ij 个车轮的驱动、转向等相应执行机构的主动调用状态为停用或使用，进而实现主动执行器配置方案的主动或被动重构;fxij、fyij分别为沿车轮与垂直于车轮的轮胎力。随后，质心广义控制力矢量与Fxij、Fyij之间的关系可表示为

式中:Li为各轴到质心间距离;B 为轴距。

在这一数理描述基础上，建立车身质心广义控制力矢量到车轮子矢量式(5) 的映射模型如下:

式中:ΘA为布尔系数组成的轴端车轮子矢量调用矩阵，其取值可满足模型对不同类型车轮配置方案的需求，实现变结构情况下的适配［12］;NCG为映射矩阵:

2 集成控制器设计

为简化集中控制器的设计难度，本文采用自顶向下的分层控制结构［13］。上层运动控制器实现运动效果跟随，下层采用控制分配器完成目标直接力到各车轮子系统间的解算，控制框图见图2。图2中，xdes(t) 为当前时刻的运动控制目标，e(t) 为当前误差。

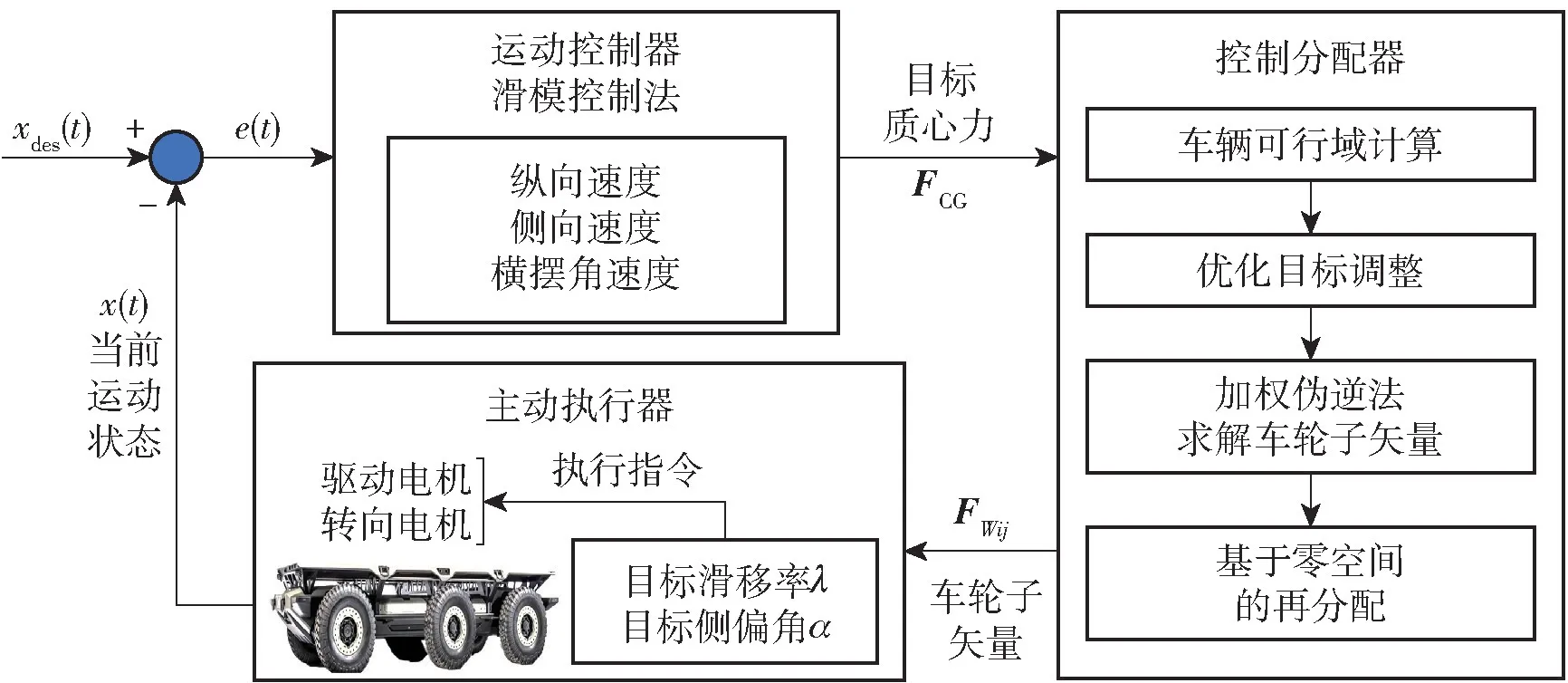
图2 集成协调控制框图Fig.2 Flow chart of integrated coordination control

2.1 运动控制器设计

对于上层运动控制器，定义［x1，x2，x3］T=［u，v，ωz］T为状态向量，xnd为理想的运动控制目标，可通过对目标工况下的转向、制动或油门输入信号解算得到，下标n 表示第n 个状态向量。

利用滑模控制器可求对目标准确跟踪的质心矢量［12］。与实际相比，存在扰动等无法建模项，考虑随有效载荷变化的参数进行不确定性建模:

式中:Mn为不确定参数;Δn为干扰项，对其上下界做约束如下:

Iz表示转动惯量的变化范围，D 为干扰项的界。

考虑到目标控制力矩与控制量之间的直接联系，将直接力控制系统的实际输出与期望值的跟踪误差定义为滑模面。系统趋近过程的轨迹对于系统稳定性控制的动态品质有着重要影响，滑模控制的目标是使设计的曲面sn(t) 保持在零附近，可以通过选择满足滑动条件的等速趋近律来实现，并用不连续控制项对系统扰动进行补偿，得到控制律如下:

式中:kn为约束参数，表征系统抑制干扰的能力，其取值对控制效果及速度存在影响，因此设计参数自适应律使其一直处于理想值，

式中:rn为正常数。为减少滑模过程中可能引起的抖振现象，用边界厚度为Φ 的线性饱和函数来替代符号函数:

综合上述各式，鲁棒自适应滑模控制率为

2.2 控制分配器设计

控制分配器将完成目标质心矢量到车轮子矢量的分配。首先对可行域进行建立:

在底盘坐标系Owxwywzw中将广义执行器的物理限制转化为对轮胎力的约束条件，以应用于优化分配算法中，如图3 所示。约束条件包括:考虑电机驱动的特性与转矩极限约束;车轮转角受其悬架系统与转向系统工作范围的约束，并将侧偏角与侧向力近似处理为线性关系。此外，考虑轮胎纯纵滑(不考虑侧偏角影响，α=0 rad) 及纯侧偏(不考虑滑移率影响，λ=0) 工况下，其纵向轮胎力与侧向轮胎力的峰值限制，建立纵滑-侧偏联合工况下车轮子矢量受到的摩擦圆约束作为车轮附着范围，通过式(21) 来描述。

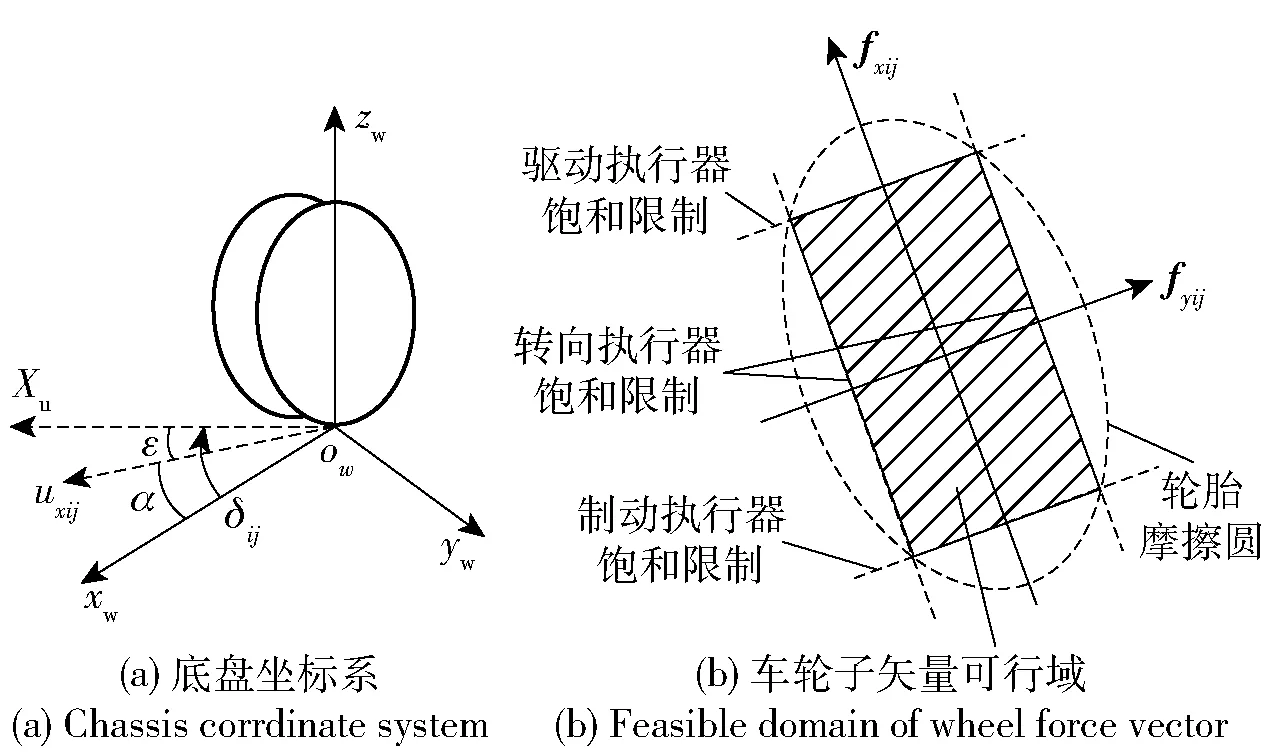
图3 车轮子矢量可行域Fig.3 Feasible region of WFV

式中:μp，ij为各车轮的摩擦系数。

以上建立了执行器及轮胎的饱和幅值限制对车轮子矢量的不等式约束条件，共同构成了车轮子矢量在轮胎力分配中的可行域:

2.2.1 基于矩阵零空间的再分配加权伪逆算法

在分配优化问题中，将期望质心矢量作为虚拟控制输入v(t)=FCG，结合既定主动执行器调用矩阵设置Θij，在相应的约束条件范围内寻找满足优化函数的执行机构控制输入向量u(t)=FW。

考虑控制实时性、分配结果期望性能指标，利用L2范数可自主考虑控制变量的符号保持特性，将混合优化目标函数设计如下:

根据文献［14］可将优化问题转换为等价形式:

式中:Wu1、Wu2为等效权重系数矩阵。

在需要进一步调整车轮子矢量分配策略的情况下，主动执行器调用配置和调用优先级可通过模型重构控制实现;此外，分配目标的优先级也可由分配算法目标函数中的权重矩阵调节。

2.2.2 再分配加权伪逆算法求解

易知，对于凸优化问题，局部最优解即为全局最优解，采用加权伪逆法，令拉格朗日乘子为λ=［λ1λ2… λn］T，并定义控制分配优化问题式(25) 的拉格朗日函数为

根据多元函数的极值条件得初始伪逆解:

式中:E、D 为解得的参数矩阵。但初始分配值仅考虑了等式约束条件，无法考虑执行器作动幅度和速率等限制。采用基于零空间特性的再分配伪逆算法［15］可对分配结果进行二次调节，使初始分配值在修正后重新落入执行机构的可行域内，从而实现高效的分配，且更便于工程实现。

首先，将初始分配值矩阵uu，k+1按照执行器的饱和约束条件进行分块，k +1 表示下一时刻。不满足条件的初始分配元素构成的行子块为uu，k+1(1)，反之行子块为uu，k+1(2)，相应正交基同样进行分块，并分别对其修正。将矩阵定义为通过相应元素的不等式约束条件进行上下界修正后的行子块:

由控制效率矩阵零空间的定义可得，对于控制效率矩阵H，其零空间的任意向量x 可由其正交基S 表示，K 为待调节的参数矩阵:

同时，根据零空间的特性，修正后的分配值也满足等式约束，即

为了系统地解算具有更好的实时性，采用链式分配法则进行求解。矩阵代入初始分配值:

在调节参数矩阵时，若只需考虑控制实时性的要求，其通常选取右逆矩阵来求解参数K，则相应控制变量调节为

若调节后控制变量满足执行器饱和约束条件，则为车轮子矢量的控制分配可行解;否则，继续应用上述链式求解步骤再次修正，直到得到控制分配问题的可行解，算法结束。

整体求解流程如图4 所示。

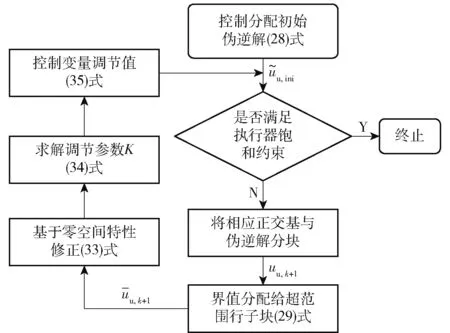
图4 再分配伪逆算法流程图Fig.4 Schematic diagram of RWPI

通过上述步骤，即可完成从质心处的直接力矢量到各车轮子矢量的优化控制分配，得到满足质心运动控制所需子矢量控制组合:

2.3 主动执行器设计

2.2 节得到的RWPI 解式(36) 即为一个包含车轮纵向力、侧向力的子矢量矩阵FW=［fxij，k+1，fyij，k+1］T，采用轮胎力解析逆模型［16］方法将纵向轮胎力、侧向轮胎力的控制目标映射成为对应的轮胎目标滑移率λd和目标侧偏角αd。选取控制精度高的经典控制算法来实现对于驱动电机和转向电机的精准控制。

结合车辆运动状态参数信息可以将对应轮胎的目标侧偏角［17］转换为转向执行器操纵指令δd:

结合车轮当前转角信息，主动转角控制量为

式中:δk为各车轮当前转角信息。

根据车轮旋转动力学模型，可得分布式车辆各轮的电机转矩Te与滑移率之间的关系如下:

式中:a1、a2、a3为参数。

考虑到轮胎-路面系统具有较强的非线性特性，且包含有时滞、载荷变化等不确定因素，因而选择鲁棒性较好的滑模控制方法对轮胎滑移率进行控制。选取滑模面sλ=τ1eλ和指数趋近律如下:

式中:τ1为调节系数;kλ、kp为约束参数。

结合式(39)，可得到滑移率控制下驱动转矩输出计算式:

综上，即完成了从优化分配算法输出的车轮子矢量到主动执行器的执行指令生成环节。

3 结果验证

本文基于一台6 ×6 分布式驱动全轮转向原理样车进行试验验证，并依据实车全部参数配置在MATLAB/Simulink 环境中搭建了虚拟样机进行仿真分析，其详细参数如表1 所示。

表1 车辆系统参数Table 1 Vehicle system parameters

3.1 仿真分析

为了分析控制算法在转向工况下的效果，提高测试工况中控制难度，将路面条件设计为μ=0.35的湿滑路面，进行初始车速30 km/h 的变速蛇形转向工况仿真计算。车速经过14 s 加速到70 km/h，前轮转向角预设周期为10 s，振幅为0.25 rad 的正弦波。并采用常用的基于规则的分配(RB)、二次规划优化分配(QP) 方法作为对照。

由图5 可以看出，三种被测方法均能够对车辆的稳定性进行有效控制，但由于分配方式的不同，其运动状态跟踪效果存在明显差异。由质心侧偏角作为侧向运动跟踪状态反馈，RWPI 法最大跟踪误差分别为速度1.66 km/h、质心侧偏角0.067 7 rad、横摆角速度0.267 rad/s，较其他两种方法降低了30%～60%，在3 种测试方法中最为精准稳定。

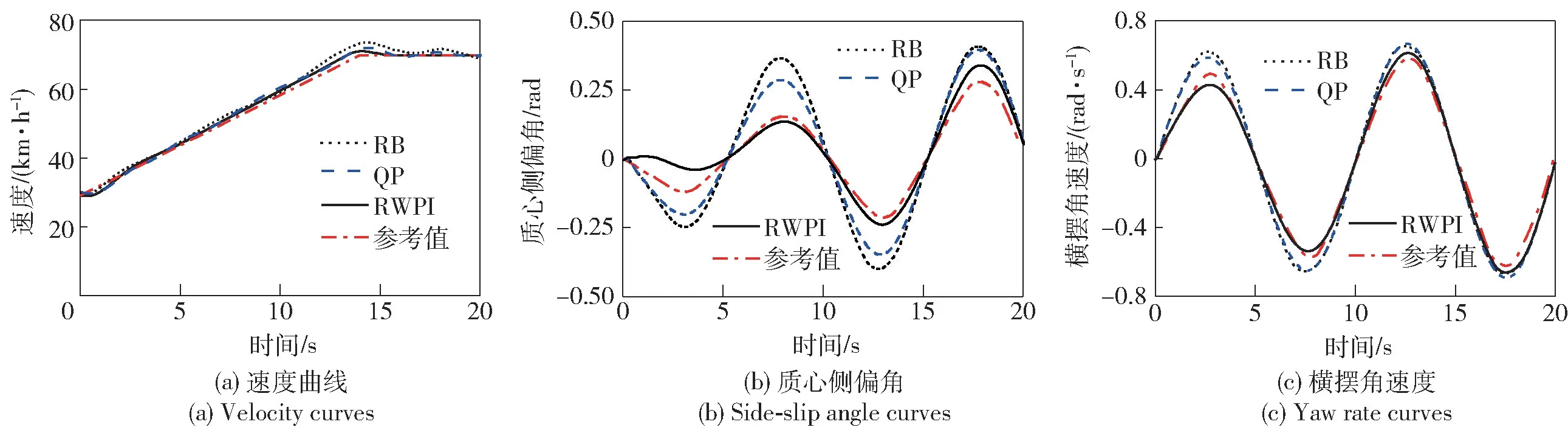
图5 加速蛇形工况实验结果Fig.5 Results of slalom test

图6 为3 种方法控制下各轮纵向轮胎力与横向轮胎力仿真结果。由图6 可以看出，基于规则的分配方法虽然计算简单，但未将执行器约束考虑在内，因此变化幅值最大。QP 算法与RWPI 算法获得的纵向轮胎力大小相近，变化趋势较为一致。侧向轮胎力中RWPI 法在各个车轮出的轮胎力变化幅度最小，因此在蛇形转向过程中产生的质心侧偏角及横摆角速度较小，车辆的稳定性得到了有效控制。

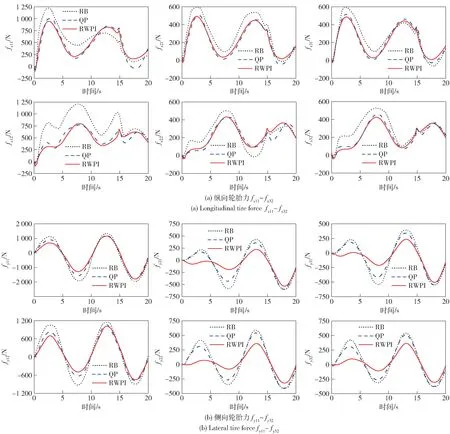
图6 加速蛇形工况轮胎力Fig.6 Tire force of slalom test

图7 体现了低附着工况下的分配控制器作用效果。分配后的轮胎力在质心处的合力可以更清晰地看出，通过对车轮子矢量的协调控制实现了对质心力目标的跟踪，其中RWPI 算法对质心力的跟踪误差均为最小，QP 算法得到的纵向力跟踪效果同RWPI 法较为接近，但侧向力及横摆力矩相差较大，RB 算法跟踪的各项跟踪误差均为最大。

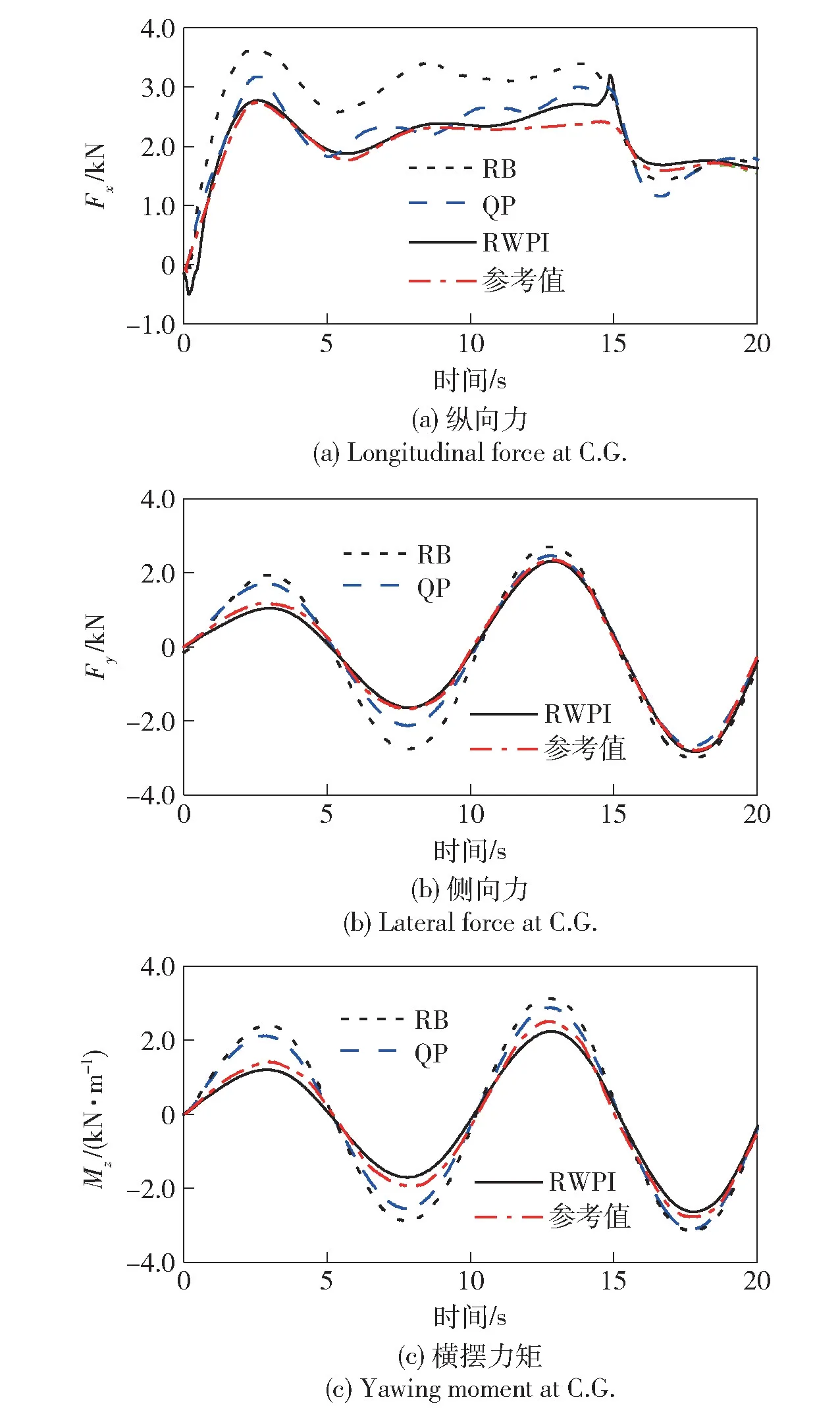
图7 加速蛇形工况质心力Fig.7 Results of forces at C.G.

3.2 试验验证

为验证控制策略在实际应用场景中的效果，试验选取了单移线工况，采用图8 所示三轴试验车辆在干燥的沥青路面条件下对上述方法进行试验验证，模型选用全轮转向全轮驱动模式，并与基于规则的平均分配算法(RB) 控制效果相对比。试验条件:车速为30 km/h，车轮输入最大转角为0.4 rad。试验结果由传感器采集，如图9 所示。

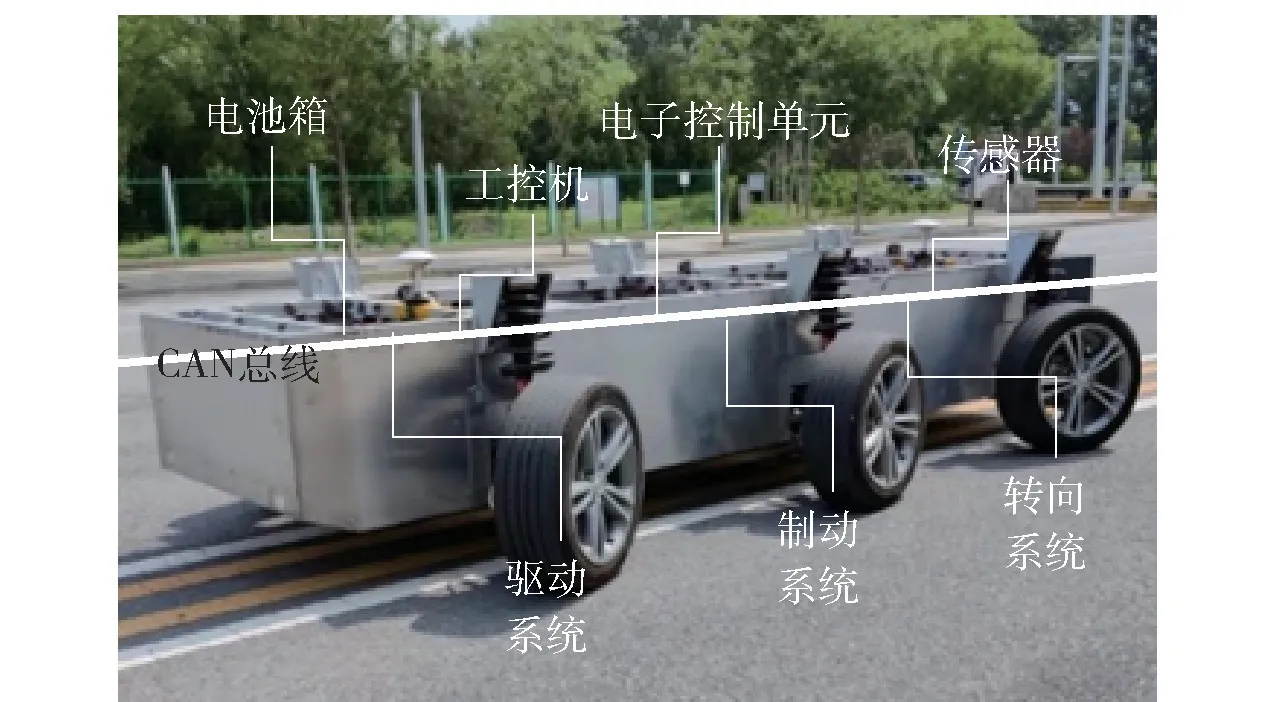
图8 原理样机Fig.8 Picture of prototype

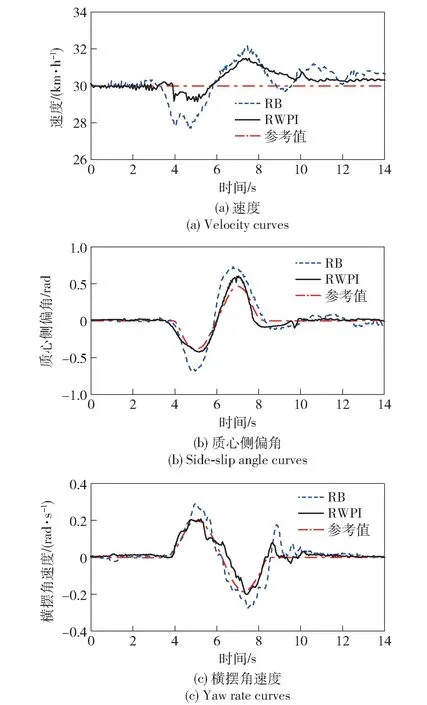
图9 单移线工况试验结果Fig.9 Results of single lane change test

从图9 中可以看出:在单移线的试验过程中，分配控制后的车辆稳定性优于RB 控制的工况，车速、横摆角速度以及质心侧偏角的峰值都明显降低，其中车速峰值降低35%，稳定时终值较RB 控制工况降低25%;RWPI 的横摆角速度峰值相较于RB 控制工况降低了25%;质心侧偏角峰值最多减小了40%，在转向过程中达到了良好的控制效果。车辆动力学参数的变化与前文分析相吻合，验证了本文所提出的控制策略。

执行器主动转矩分配的结果如图10 所示，从中可以看出RWPI 算法作为控制分配器时，在单移线试验过程中将主动执行器充分利用，合理调配，根据执行器潜力在可行域内进行理想的分配，并成功实现对整车的稳定控制效果。图10 中，Tij表示各电机转矩，i 表示轴，j 表示左右侧。

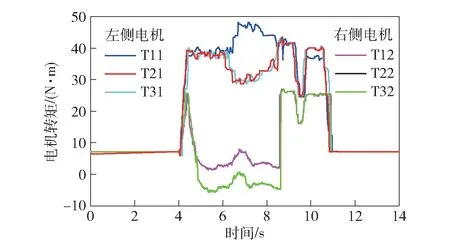
图10 主动转矩试验结果Fig.10 Results of torque after distribution

4 结论

本文以多轮分布式独立电驱动车辆作为研究对象，考虑过驱动系统的冗余问题，设计了可重构的控制分配策略。得出主要结论如下:

1) 建立了车轮子矢量与质心力之间的联系，引入可重构因子实现变结构，适用于多种模式的车辆运动工况。

2) 分配控制器通过考虑了参数不确定性的滑模控制器生成质心力控制目标，实现对运动目标的跟踪效果。进而通过加权伪逆算法对车轮子矢量进行求解，其权重系数可以对优化目标进行调节，最后基于零空间理论，采用链式分配法则对伪逆解再分配，最终得到控制分配的可行解。

3) 为验证分配控制器有效性，在典型工况下分别进行了仿真验证和实车试验，结果均达到了效果预期。控制分配方法能够对目标进行有效跟随，并对车辆行驶稳定性具有改善作用。

4) 下一步研究可以在约束设计方面，对所提出的分配算法的有效约束问题进行进一步优化，对力矩的约束范围进行补充分析。