多作动器协同的特种车辆行车调平控制方法

张聪，刘爽，姜思远，刘世纪

(1.燕山大学 电气工程学院，河北 秦皇岛 066004;2.河北省工业计算机控制工程重点实验室，燕山 大学，河北 秦皇岛 066004)

0 引言

特种装备车辆需要具备在行驶中调平车身姿态的能力，为车载专用装置正常运行提供平稳的支撑条件。当前普遍采用的支腿式驻车调平方式无法满足特种车辆行车调平的使用需求。例如，防空作战领域的新宠——激光武器作战车，在追击无人机等目标时需要保持车身水平，便于车载高能激光武器将激光光束锁定目标某一点持续照射，实现能量攻击。又如，千吨级的大火箭活动发射平台［1］，在将长征五号等大型运载火箭垂直转运至发射区的过程中，需要时刻保持水平，以确保运载火箭绝对安全。再如，举高消防机器人，跟随火势实施机动举高喷水作业时，需要底盘始终保持水平，防止高举臂架的机器人发生倾倒。还有，高地隙喷雾机［2-3］，在山坡作业时需要实时保持车身水平，既防止侧翻，又避免对农作物造成损伤。可见，特种车辆的行车调平技术是国防军事、航天发射、应急救援、农业生产等关系国计民生重要领域的共同需求。

通过对悬架系统施加主动控制实现特种车辆的行车调平是最为直接和有效的方法。1954 年美国GM 公司Erspiel-Labrosse 在悬架设计中首先提出了主动悬架的概念。主动悬架通过作动器产生主动控制力，可以在较大带宽范围内等效任意刚度和阻尼特性，作动器伸缩完全可控，使得车身位置和姿态完全可控，是用作特种车辆行车调平执行机构的不二之选。通用车辆的主动悬架控制技术已经发展多年，并已逐步趋于成熟，主要是利用其等效任意刚度和阻尼特性的特点，提升车辆的驾乘舒适性［4-6］和操控稳定性［7-8］。如果考虑节能因素，可变阻尼的半主动悬架控制技术［9-11］则更加符合通用车辆的使用需求。然而，与通用车辆主动悬架控制专注于行驶过程中的舒适平稳极为不同，特种车辆行车调平更为注重行驶过程中车身姿态的保持。显然，作动器伸缩完全可控的特性使得主动悬架更加适合用于解决特种车辆的行车调平问题。

现有主动悬架行车调平方法，普遍基于整车垂向动力学模型［12-13］，结合各种先进的控制理论［14-20］解决行车调平中的各种问题。文献［12］基于双环自抗扰解耦技术和分数阶PID 力跟踪控制器，实现车身位姿的稳定控制，解决行车调平中通道耦合及作动器抗扰伺服控制问题。文献［13］提出基于位移控制的主动悬架系统控制策略，实现高机动性应急救援车辆的位姿稳定控制，避免以力为被控量的液压伺服控制易在冲击作用下发生突变的问题。文献［14］考虑主动悬架具有硬约束的情况，提出一种自适应反推控制策略，使车身的垂向和俯仰运动在预定时间内保持恒定，进而提高乘坐舒适性。文献［15］提出加入悬架挠度积分作用的最优控制器，得到各个作动器的期望控制力，同时调控车身位姿保持恒定，很好地抑制了转弯和制动过程中的车身姿态变化，而且在行驶舒适性和道路友好性方面都有很好的表现。文献［16］研制了一种新型的并联主动杆悬架，设计鲁棒控制方案，在最小化俯仰角和侧倾角的同时，提高了车辆的驾乘舒适性和操控稳定性。文献［18］研究了事件触发H∞主动悬架控制方法，实现车身位姿稳定控制。

整体而言，上述行车调平控制方法的研究思路都是基于整车垂向动力学模型，设计以调控车身俯仰角、侧倾角和身质心铅垂高(车身质心空间绝对垂向位移) 为目的控制器。参考文献［11 -12，21 -22］，给出7 自由度整车模型示意如图1 所示，在原有被动悬架基础上，对应车轮增加4 路独立作动器施加主动控制力Fc，1、Fc，2、Fc，3和Fc，4，θ 和φ 分别表示车身俯仰角和侧倾角，la和lb分别表示前轴、后轴到质心的距离，lc和ld分别表示车轴左侧和右侧到质心的垂直距离，一般情况lc=ld=1/2轴长。

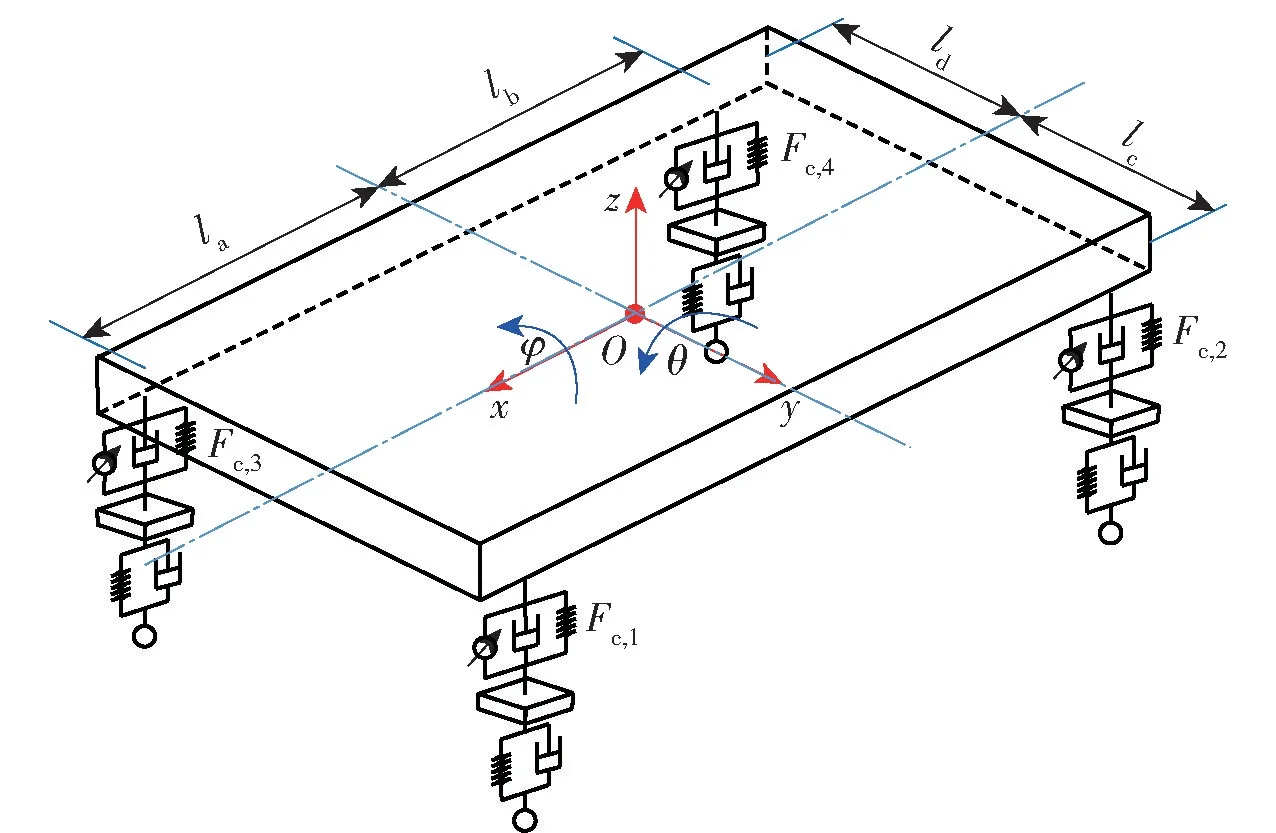
图1 7 自由度整车模型示意图Fig.1 7-DOF vehicle model

归纳以上参考文献中的整车建模过程，可将7 自由度整车垂向动力学模型抽象为如式(1) 所示的状态空间方程形式:

式中:X=［zs，θ，φ］T为被控状态，zs、θ 和φ 分别为车身质心铅垂高、俯仰角和侧倾角;Fc=［Fc，1，Fc，2，表示Bc的右逆矩阵Fc，3，Fc，4］T表示控制输入，为与4 个车轮相对应的作动器的直接输出力;Bc为控制增益，Bc=表示簧载质量，Jy表示俯仰转动惯量，Jx表示侧倾转动惯量;Fx=［fx1，fx2，fx3］T表示控制力以外的合力，包括弹性力、阻尼力、重力和通道间耦合力等。

在模型精确，且不考虑垂向动力学与纵向及侧向通道间耦合情况，参考文献［11 -12，22］，归纳当前整车型行车调平控制算法的基本形式如式(2)所示:

此类方法存在以下两方面的问题:

1) 模型形式不利于控制器的设计和实现。其一，模型式(1) 为四入三出的超静定形式，由于系统输入数量大于被控状态的数量，在算法式(2) 执行过程中，需要求解Bc的右逆矩阵，十分麻烦。其二，直接以X=［zs，θ，ϕ］T为被控状态，需要对位移和姿台的混合调控，参数整定相对困难。

2) 将车身质心铅垂高zs作为被控量，算法式(2) 必须假设其可精确测量。然而，生产实际中无法通过外部标定等方式对车辆的空间坐标进行测量，车身铅垂高无法精准获取。因此，对车身质心铅垂高的依赖是制约行车调平实现的突出技术瓶颈。

鉴于此，本文在磁浮列车悬架系统多点协作［23］和多无人机协作搬运［24］等实例的启发下，基于多智能体一致性协同控制思想［25-26］，提出多作动器协同控制的新思路，进而给出切实可行的特种车辆的行车调平新方法。本文的主要贡献为:

1) 针对问题1，将整车垂向模型分解为由作动器驱动的带有相互耦合特性的多智能体悬架节点，建立悬架节点动力学模型。将基于超静定整车垂向动力学模型的位姿混合控制问题，转换为基于全驱型悬架节点动力学模型的单纯位移控制问题。

2) 针对问题2，构建基于悬架动行程的趋势引导动态基准和基准误差，摆脱调平算法对车身质心铅垂高的依赖。

3) 提出基于动态基准误差的多作动器协同行车调平方法，实现特种车辆的行车调平，提升调平精度。

需要指出，本文提出的多作动器协同方法，专指悬架节点之间的协作行为。这与现有研究中悬架系统与转向系统［27］、制动系统［28］、车身稳定系统［29］等的协调设计，以及将转向、制动、发动机等系统划分为多个智能体［30-31］进行协调设计的思想和方法均不相同。

1 系统建模

本文特种车辆的主动悬架系统如图2 所示，其采用液压作动器直接代替弹簧阻尼被动悬架系统，通过控制液压顶杆伸缩，可使车身位置和姿态完全可控。

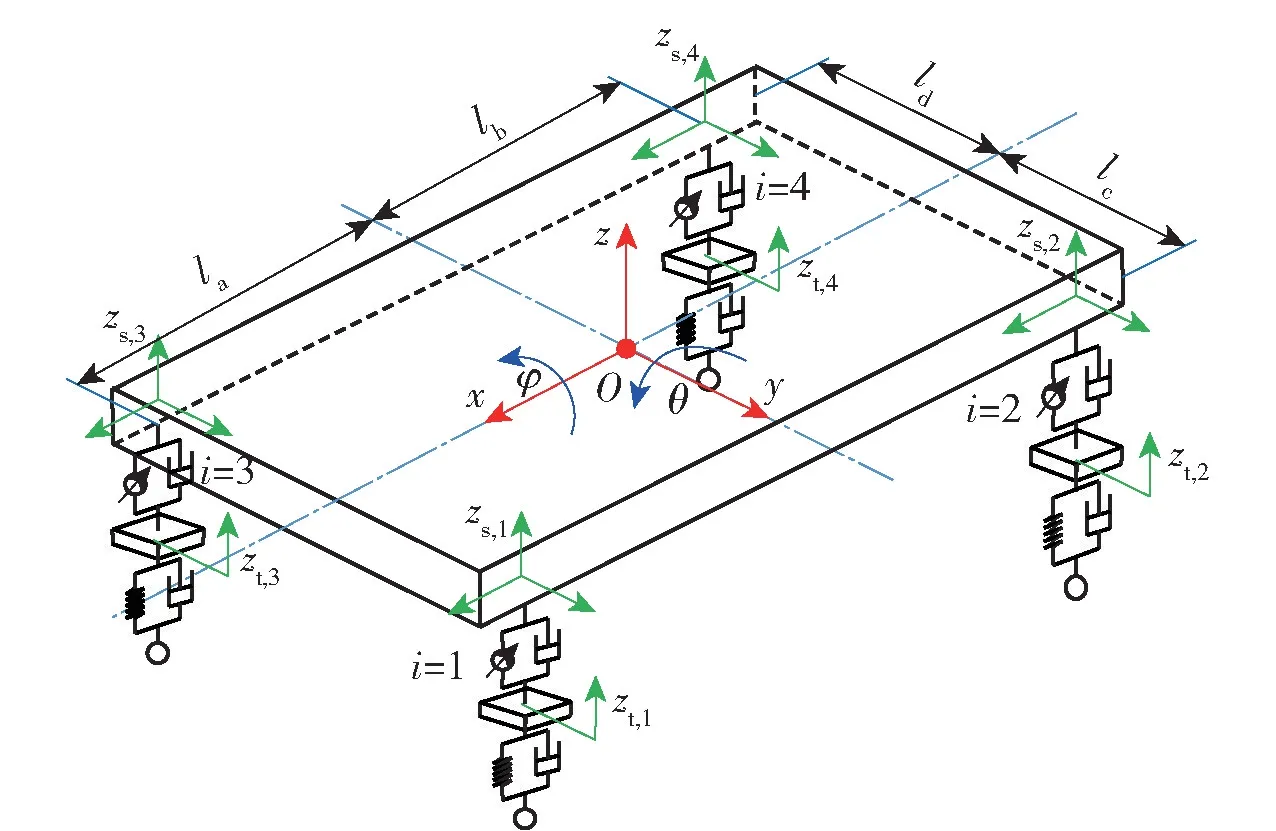
图2 独立驱动的液压主动悬架系统示意图Fig.2 Independent hydraulic active suspension system

区别于传统四轮车辆直接以簧载部分位姿的3 个变量及非簧载部分垂向位移的4 个变量为系统状态的7 自由度整车动力学模型的建立方式，本文按照车轮数量将整车划分为相对独立的悬架节点i(i=1，2，3，4)，将悬架节点簧载部分及非簧载部分的垂向位移作为系统状态，建立系统模型;建模时又区别于传统多智能体节点间相互独立的情况，需要考虑悬架节点间固有的耦合作用。悬架节点i 的动力学模型，如式(3) 所示:

式中:下标i=1，2，3，4，依次表示左前、左后、右前和右后4 个悬架节点;针对悬架节点i，zs，i表示簧载部分的垂向位移;ms，i表示等效簧载质量;mt，i表示等效非簧载质量;Gs，i=-ms，ig 表示等效重力，g 为重力加速度表示作动器等效阻尼力，cs表示作动器等效阻尼系数;Ft，i=kt(zr，i-zt，i) +分别表示轮胎等效弹性力和阻尼力，kt和ct分别表示轮胎等效刚度和等效阻尼系数，zt，i表示非簧载部分的垂向位移，zr，i表示所受路面激励的垂向幅值;Fcp，i表示节点间的耦合力，主要体现为作动器合力间耦合、重力耦合及角动态耦合。

2 多作动器协同控制方法设计

2.1 设计思路

在特种车辆行驶中，如果所有悬架节点簧载部分的铅垂高能够时刻保持一致，并跟踪同一基准，就能实现行车调平，这即是多作动器协同实现行车调平的基本思想。悬架节点动力学模型式(4) 的建立为系统特性分析和调平方法设计奠定了基础。同时也反映出多作动器协同行车调平控制与多智能体一致性协同控制的区别。多智能体协同一致性一般研究的是相互独立个体之间的协同控制问题，因此，其侧重于解析不同信息传递机制与控制之间的相互作用规律。多作动器协同行车调平控制研究的是固连于车身的悬架节点间的协同控制问题，悬架节点间必然存在耦合作用，在悬架节点动力学模型式(4)中表现为耦合项Fcp，i。另外，由于车辆具备完善的总线信息交互机制，在行车调平控制时，可选用全部悬架节点间两两连通的连通性最强的拓扑进行多作动器协同算法设计。因此，多作动器协同行车调平控制研究更需要关注的是处理好各个悬架节点间之间的受力耦合。悬架节点之间存在的耦合作用是悬架节点系统与多智能体系统之间的本质区别。只要解除耦合，便可将多智能体一致性协同控制的相关理论［25］移植到行车调平的方法设计中。

2.2 动态基准误差

构建不依赖车身质心铅垂高的动态基准误差是实现行车调平协同控制的前提。与整车型行车调平方法中将基准状态设为常值的做法不同，本文基于各个作动器的动行程设计实时动态调整的趋势引导动态基准及基准误差。

首先，构建动态基准如式(4) 所示:

式中:下角标m 表示导数阶次，m=0，1;nl表示作动器压缩的悬架节点数量之和;nk表示作动器伸展的悬架节点数量之和;Ωl表示所有作动器压缩悬架节点的集合;Ωk表示所有作动器伸展悬架节点的集合;为一常数，表示预设行程中位偏移量，用以根据路面情况调解作动器上下行程范围。

其表示相对于车辆静止时各个作动器的平衡中位，所有压缩作动器对应的非簧载部分运动状态的平均值与所有伸展作动器对应的非簧载部分运动状态的平均值之和再除以2。

特别地，全部作动器处于压缩状态时nk=0、nl=n，全部作动器处于伸展状态时nk=n、nl=0，n表示悬架节点总数量，h=hl+nk。此时，动态基准通过式(5) 进行计算

作动器的压缩伸展如图3 所示。式(4) 和式(5) 表征了全部作动器的整体运动趋势，称为基于动行程的趋势引导动态基准，其可确保动态基准不会超出行程范围。动态基准的上下边界由式(5)限定，上下界分别为作动器的压缩极限和伸展极限。当作动器全部完全压缩，得到动态基准上限;当作动器全部伸展时，得到动态基准下限。其他情况时，动态基准将介于悬架行程范围内。

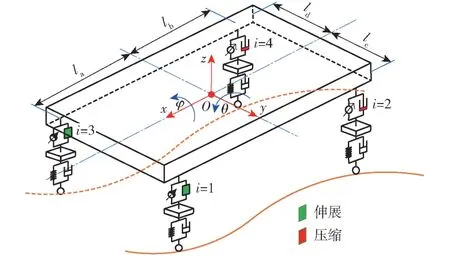
图3 作动器压缩伸展示意图Fig.3 Actuator compression and extension

其次，构建动态基准误差。式(4) 和式(5) 需要根据非簧载部分的空间垂向运动状态计算得到，这在实际中无法实现。幸运的是，本文算法并不需要直接计算动态基准式(4) 和式(5)，真正需要计算的是悬架节点i 簧载部分的运动状态与动态基准之间的差值，即，如式(7) 所示:

特别地，全部作动器处于压缩状态时nk=0、nl=n，全部作动器处于伸展状态时nk=n、nl=0。此时，悬架节点i 簧载部分的垂向状态与动态基准状态之间差值的需要通过式(8) 进行计算:

不失一般性地以悬架节点1 为例，通过计算可以得到悬架节点1 和其他节点之间的簧载部分的铅锤位移差和速度差分别如式(11) 和式(12) 所示:

如此，得益于动态基准式(4) 和式(5) 的巧妙设计，悬架节点i 与动态基准之间的垂向状态差值式(7) 和式(8) 的获取摆脱了对铅垂高的依赖。

2.3 协同调平算法

多作动器协同算法是实现车身位姿稳定调节的核心。按照本文设计思路，基于文献［26］的定理5.8，考虑所有悬架节点均能获取基准状态信息，且各个节点两两连通的情况，针对悬架节点i，设计多作动器协同算法，如式(13) 所示。即可保证所有悬架节点簧载部分的垂向位移和垂向速度分别趋于一致，进而实现整车的行车调平控制。显而易见，算法式(13) 不仅考虑了各个节点的动态基准状态误差，而且考虑了节点间的状态误差，这更有利于各个节点的运动趋于一致:

式中:通过-Fcp，i解耦合，通过-Fs，i-Gs，i进行反馈线性化，将系统等效为双积分动力标准模型，其余项为针对双积分标准型动力系统的一致性协议;zs，i-zs，0和·zs，i-·zs，0分别表示悬架节点i 簧载部分与动态基准之间的位置和速度差;zs，i-zs，j和·zs，i-·zs，j分别表示悬架节点i 簧载部分与其连通节点之间的位置和速度差;γ 表示算法中位置偏差和速度偏差的权重分配，选取0 ＜γ ＜1;a0反映算法中i 节点的状态与动态基准间误差所占权重，选取a0＞0，每个节点都能获取基准信息;ai，j反映算法中节点间相对状态误差所占权重，鉴于车辆的结构对称性和完善的总线信息交互机制，可选取ai，j为相等的正常数，保证所有悬架节点间为两两连通的无向连通拓扑。

算法式(13) 中，悬架节点之间的垂向状态之差可以依据几何关系式(9) 和式(10) 计算得到，不再赘述。

如此，通过动态基准误差的巧妙选取及悬架节点间固有的几何关系，算法式(13) 摆脱了对簧载部分铅垂高测量值的依赖，这正是多作动器协同算法突破现有整车型行车调平方法技术瓶颈的关键点。

2.4 稳定性分析

车辆的主动悬架系统模型包含簧载部分和非簧载部分的动力学，上述多作动器协同算法式(13) 基于悬架节点簧载部分的动力学而设计，定理5.8［26］可以确保簧载部分闭环系统的稳定性和渐进一致性。因此，在此只需要讨论非簧载部分的零动态稳定性，以确保整个主动悬架系统的闭环稳定性。

分析非簧载部分的零动态稳定性时，需将簧载部分的系统输出置零，即令zs，i=·zs，i=0。此时，Fc，i=-Gs，i，则非簧载部分的动态如式(14) 所示:

写成状态空间形式为

式中:Pi是方程的正定解，Qi为一正定矩阵。

对Vi求导并进行整合和缩放，可得

式中: σmin(Qi) 表示Qi的最小奇异值;σmax(Pi) 则表示Pi的最大奇异值;‖Di‖≤Δi∈R。

由于Pi正定，由式(16) 可得

式(22) 表明只要Zt，i(0) 和Δi都有界，则Zt，i是最终一致有界的。而Zt，i(0) 和Δi有界分别表示Zt，i的初始状态有界及路面激励有界，这显然是符合现实情况的。因此，非簧载部分系统零动态稳定。进而，整个主动悬架系统闭环稳定。

3 联合仿真与结果分析

利用Carsim 与Simulink 软件联合仿真验证本文提出的多作动器协同算法式(13) 的有效性，并与被动悬架情况及整车型行车调平算法式(2) 进行对比。算法式(13) 中的参数设定为a0=100，ai，j=100，γ=0.2，算法式(2) 中的参数设定为K=diag{100，100，100}，γ=0.2。

联合仿真中直接选用汽车系统仿真软件Carsim样例车型“D-Class，SUV: 4WD，Ext，Rr.Twin Clutch Ctrl”，整车主要参数: 质量1 430 kg，轴距2 660 mm，轴长1 565 mm。悬架参数:被动悬架弹簧刚度系数为130 N/mm，阻尼系数为6 N/(mm/s)，设计行程范围为±100 mm;主动悬架采用作动器直接替换被动弹簧，保留被动阻尼，阻尼系数为6 N/(mm/s)，设计行程范围为±100 mm。仿真情形设置如下: 分别以10 km/h、20 km/h、30 km/h 的中低速驶过凹凸路面，如图4 所示。即过程中左侧前后车轮依次通过高8 cm 的凸起，右侧车轮依次通过深度为8 cm 的凹坑。

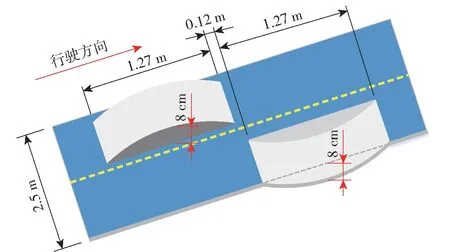
图4 路面激励示意图Fig.4 Concave-convex road excitation

10 km/h 情况的仿真结果如图5～图9 所示。图5 表明，相对于整车型调平算法，本文算法更好地实现了车辆行车调平的目标，车辆的俯仰角和侧倾角明显更小。其主要原因在于在本文提出的多作动器协同算法的作用下，各个悬架节点间簧载部分的位移和速度呈现出明显的一致特性而整车型算法式(2) 的各个节点呈现出杂乱无章状态，如图6 和图7 所示。动态行程如图8 所示，在本文提出的多作动器协同算法作用下，各作动器呈现出明显的协作特性。图9 给出两种主动悬架算法的输出控制力曲线，一方面，表明控制力均在2 000～5 000 N 的合理的范围之内，作动器足以提供所需控制力;另一方面，控制力变化平缓，未出现高频突变，作动器足以及时响应。

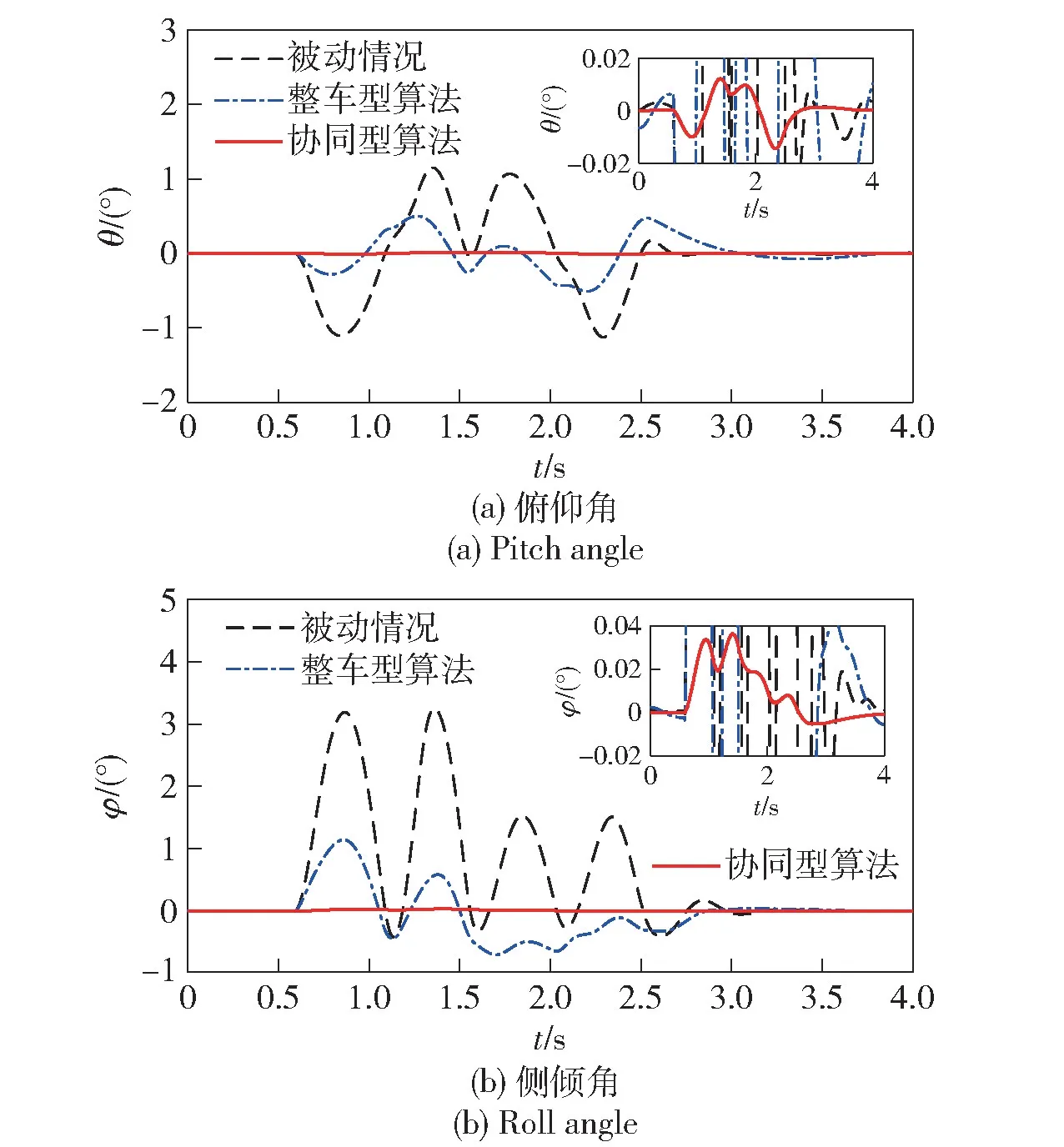
图5 俯仰角和侧倾角Fig.5 Pitch angle and roll angle

图6 悬架节点铅垂高Fig.6 Vertical height of suspension node

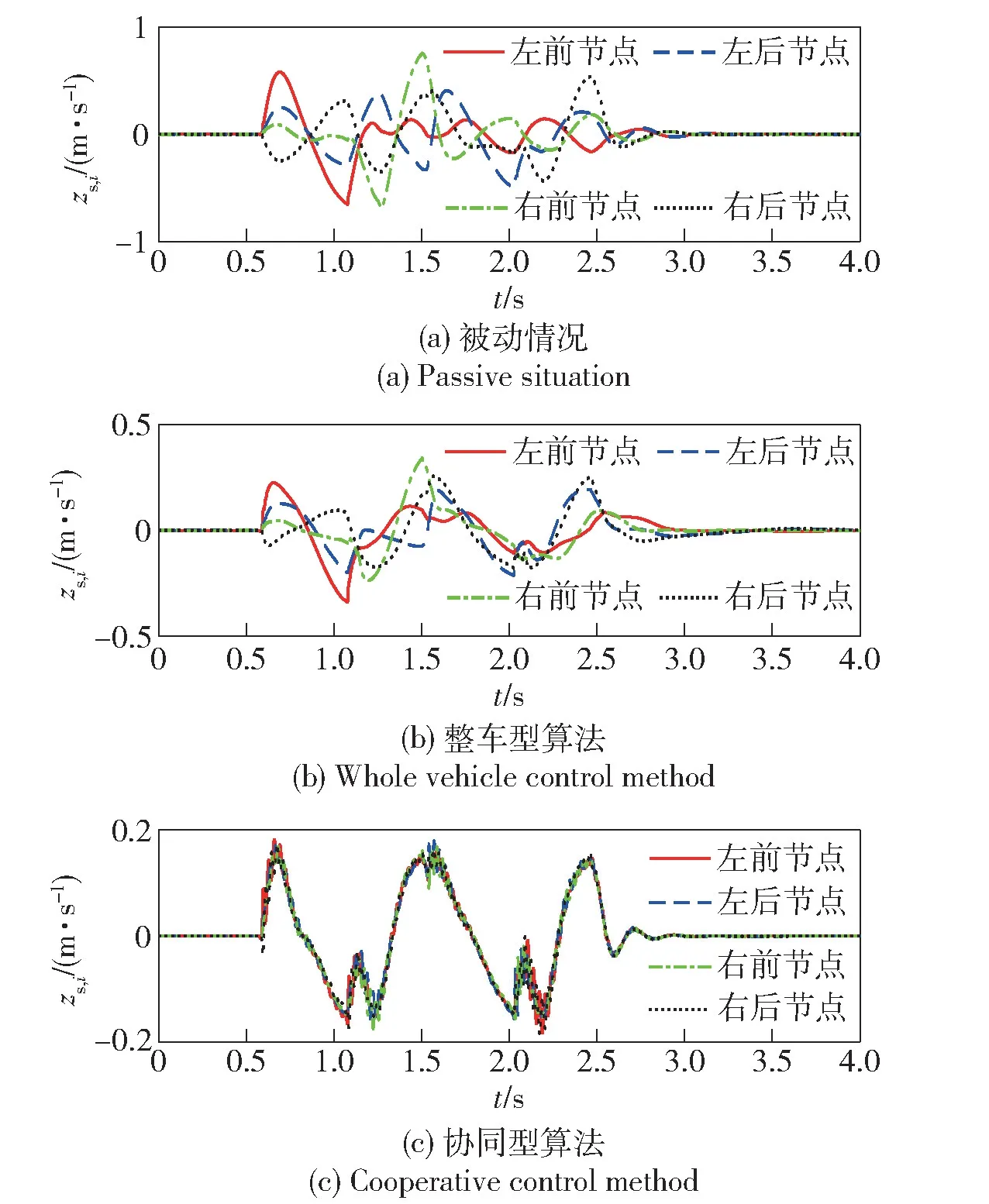
图7 悬架节点铅锤速度Fig.7 Vertical velocity of suspension node

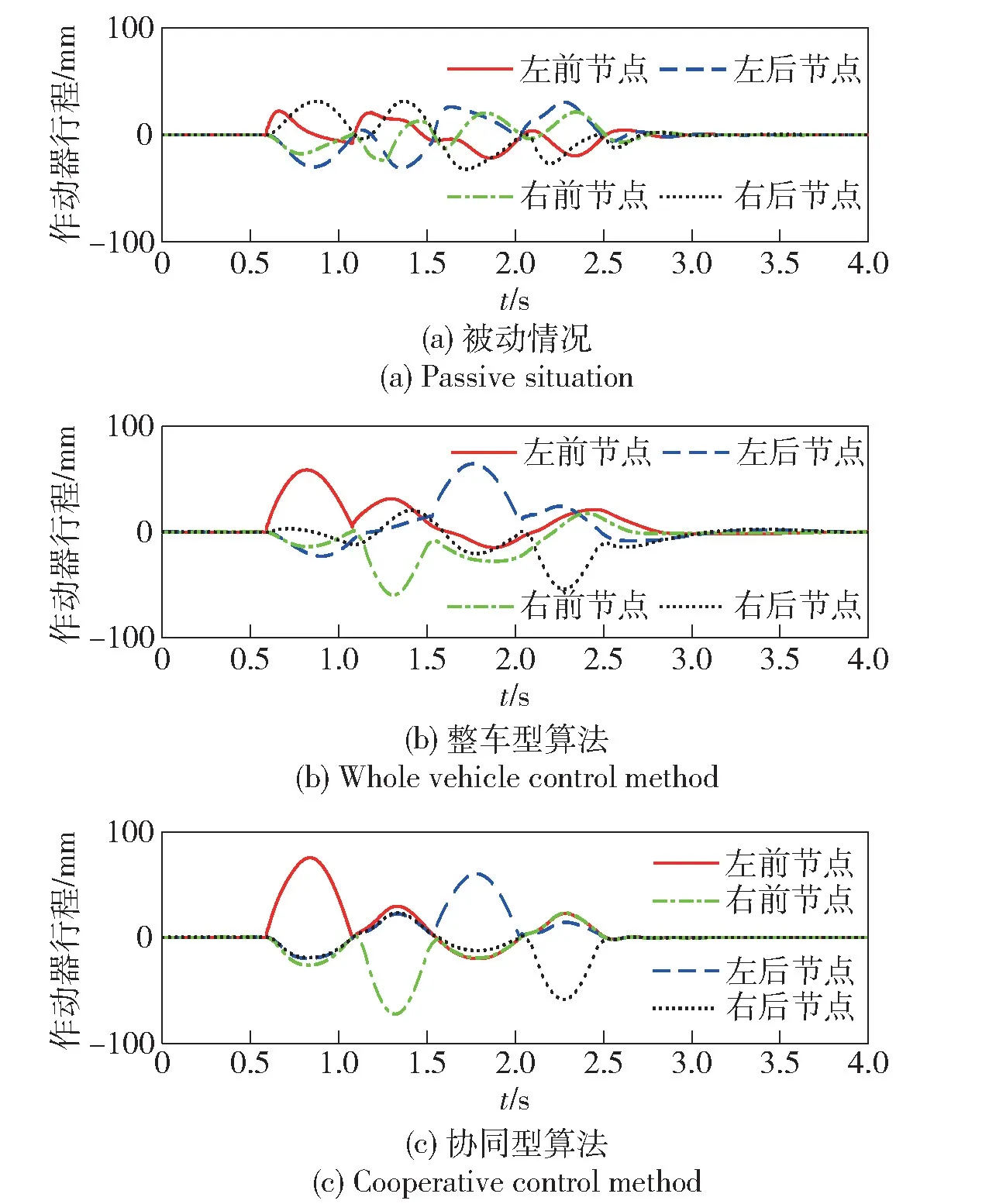
图8 作动器行程Fig.8 Suspension working space

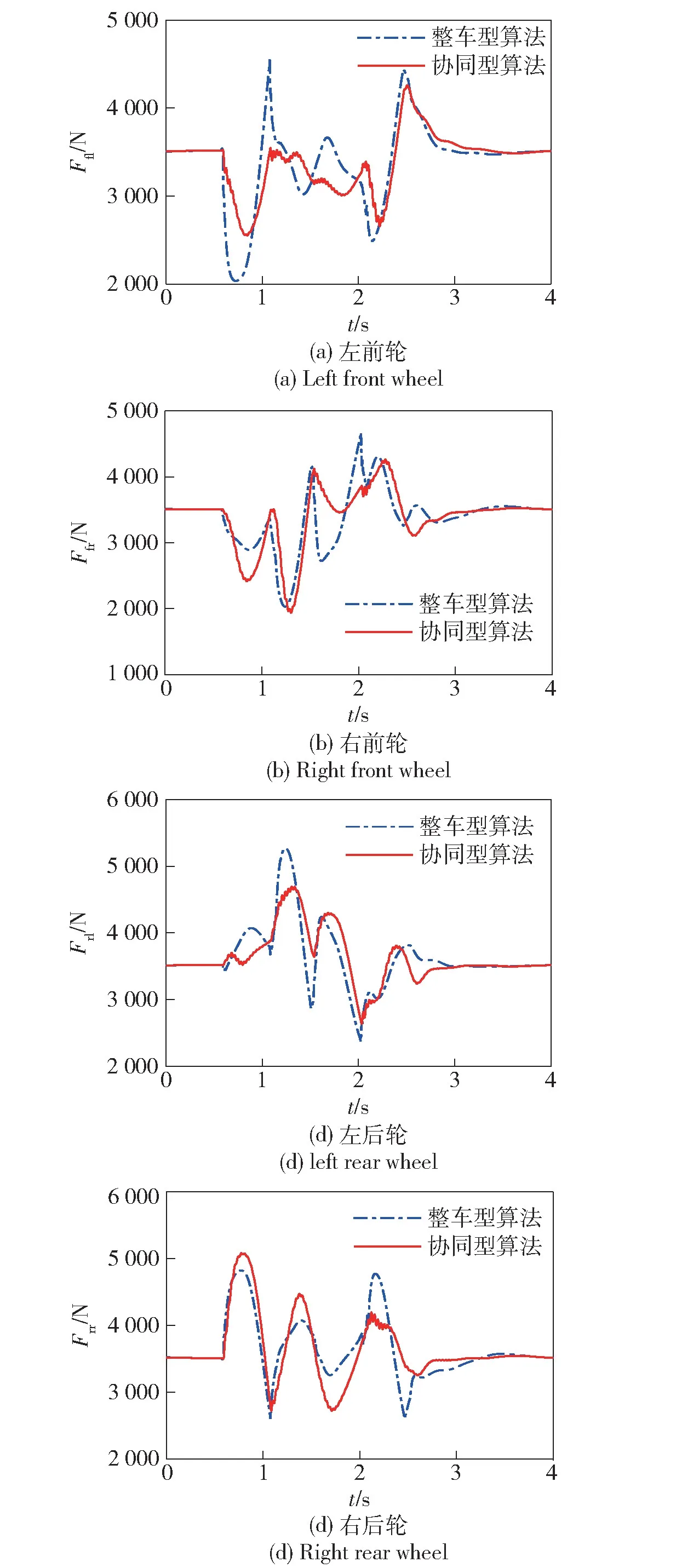
图9 控制力Fig.9 Control force

20 km/h、30 km/h 情况仿真结果与10 km/h 情况的基本类似，鉴于篇幅不再列出具体仿真结果图。对3 种情况的姿态角均方根进行统计，如图10 所示，可见在各种情况下，协同算法式(13) 均表现出更好的调平特性，控制精度提高了1～2 个数量级。如此，协同算法更适用于特种车辆追求高精度行车调平的特殊工况。另附有仿真动画，可以更为直观地呈现出车身位姿变化情况。仿真动画详见百度网盘:https:∥pan.baidu.com/s/1nquk0MpPeij8yUgWOOscug?pwd=HELP。

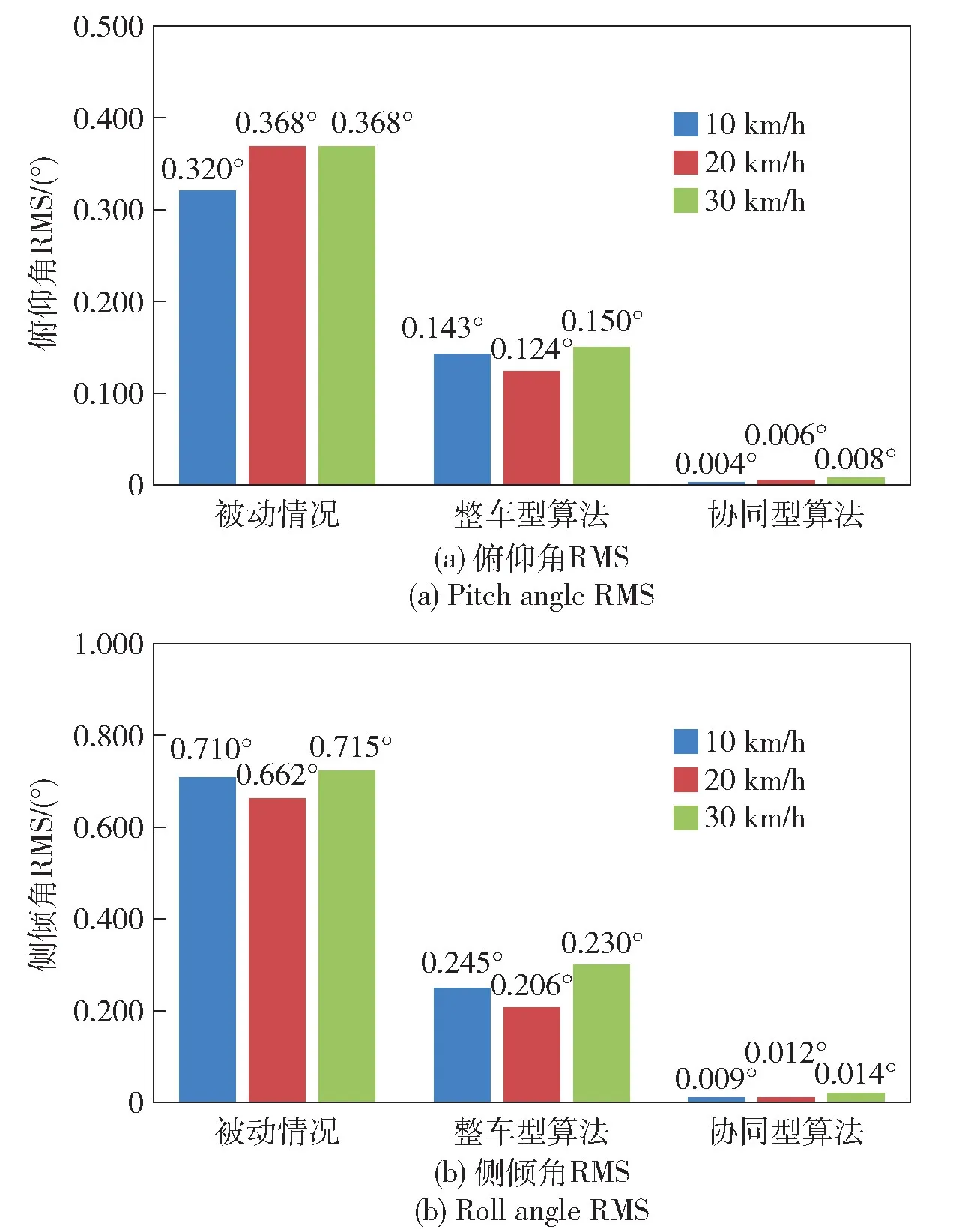
图10 俯仰角和侧倾角均方根统计Fig.10 RMS of pitch angle and roll angle

4 结论

本文所提出的多作动器协同控制方法，为特种车辆的行车调平问题提供了全新的解决思路和切实可行的具体方法，是协同控制思想在主动悬架控制研究领域的创新拓展。相对于现有整车型调平控制方法而言，多作动器协同方法将行驶中整车的位姿控制问题转化为单纯的相对位置控制问题，系统设计思路更加清晰，控制方法实现更加简单，并且突破了对车身铅垂高依赖的技术瓶颈，得到了更好地控制效果。基于本文提出的多作动器协同控制思路，后续可以针对主动悬架系统中非线性、时滞性、不确定性、预设性能、状态约束等各种常见问题开展进一步研究工作。