公铁平层宽幅钢箱梁桥面车致局部振动研究

何佳骏 谭伟 徐昕宇 李永乐

1.中国市政工程西南设计研究总院，成都 610213；2.中铁二院工程集团有限责任公司，成都 610031；3.西南交通大学 土木工程学院，成都 610031

公铁平层布置形式因具有承载能力良好、用钢量少、施工方便、外观优美等优点，逐渐应用到各种大跨度桥梁中。然而，这种形式一方面加剧了公路与铁路车辆之间的相互干扰，另一方面桥梁宽度的增加使得桥面板横向刚度下降，更容易发生局部振动。这使列车通过桥梁时引起桥面板局部振动，传递至公路车道后给其带来额外的路面不平度，增加了公路车辆的响应。这种响应与列车引起的桥梁整体振动叠加，会威胁桥上行车安全。

文献［1-2］对各种类型的桥梁进行了车-桥耦合振动分析。文献［3］对基于板壳单元桥梁模型的车-桥耦合振动分析主要分为两方面，一方面是提出简化方法使桥梁自由度下降，另一方面是建立精细化板壳单元模型研究局部振动的影响。铁路方面，文献［4］以荆岳铁路洞庭湖大桥为研究对象，基于自主研发的桥梁结构精细化三维有限元模型和31 个自由度的列车模型，研究桥梁整体和局部动力响应。文献［5］以沪通长江大桥为背景，通过提出的等效正交异性板法建立了精细化的车-桥耦合振动模型，分析列车引起的局部振动在跨中截面上的分布和对主桁架动力响应的影响。文献［6］基于板壳单元有限元模型，建立精细化列车-桥耦合振动模型，以上海崇明越江通道长江桥为背景，对比分析了杆梁单元与板壳单元模型列车-桥系统响应的差异。文献［7］测量了意大利高速铁路上的一座钢混组合梁在车致振动下的加速度，对比数值模型发现共振对桥面局部瞬态响应有促进作用。公路方面，文献［8］通过编制的车-桥耦合振动计算程序分析混凝土箱梁桥的局部振动问题，研究桥梁局部放大系数与总体动力放大系数。文献［9］以武汉市连续钢箱梁桥为背景，通过建立精细化有限元模型分析桥面局部振动，并与杆梁单元计算结果对比。

上述研究表明，桥面的局部振动可能会增大桥梁结构的动力系数，且会干扰车辆与桥面接触点周围桥面板的响应。由于公铁平层布置桥梁相关的工程案例较少，关于宽幅桥面板局部振动的研究也相对较少。因此，本文通过建立局部板壳桥梁有限元模型，分析列车通过桥梁时引起的局部振动在桥面板上的分布以及对公路车道的影响。

1 仿真算例

1.1 工程概况

在建宜宾临港长江桥为大跨度公铁平层布置双索面斜拉桥，跨径布置为（72.5+203+522+203+72.5）m。左右两个桥塔对主梁的约束并不相同，左侧桥塔耦合了主梁的纵桥向位移，右侧桥塔并未耦合。主梁宽63.9 m，桥面共设置4 线铁路以及双向6 车道，两侧悬臂端设置人行道以及非机动车道，见图1。

图1 桥梁总体布置和主梁横截面

1.2 桥梁局部板壳有限元模型及验证

车-桥耦合计算中常采用杆梁单元模型，即主梁、桥墩、桥塔采用梁单元模拟，斜拉索采用杆单元模拟。杆梁单元模型中梁单元的截面变形始终满足平截面假定，无法考虑桥面板局部变形的影响。对于宽幅钢箱梁桥面而言，较大的桥面宽度削弱了桥面板的支撑刚度，使其在车辆荷载作用下可能会发生明显的变形，且这种变形可能会引起其他车道的额外路面不平度。如果引入全桥板壳单元模型进行车-桥耦合振动计算，在分离迭代时桥面板单元过多会导致收敛时间较长，影响计算效率［10-11］。

为考虑桥面板的局部振动并提高车桥耦合振动计算效率，本文提出了一种主梁关键梁段局部采用板壳单元有限元模型的方法。建模方法如下：根据桥梁设计图纸建立桥梁的杆梁单元模型；根据主梁截面的参数，在关键位置附近选取一定长度的梁段建立板壳单元模型；采用刚臂连接同里程位置的板壳单元与梁单元节点形成刚性域。采用ANSYS 软件建立桥梁板壳有限元模型，选取跨中附近120 m 长度的梁段建立了板壳单元模型，计算时未考虑桥面系对振动的影响。桥面系对振动的传递有削减作用，因此本文计算结果会更保守。

为验证局部板壳模型的正确性，同步建立桥梁的杆梁单元模型，对比分析两种模型的静动力特性。杆梁单元模型与局部板壳模型跨中竖向位移分别为0.501 8、0.495 5 m，两个模型自振特性对比见表1。可知，两个模型跨中竖向位移误差在1%左右，自振频率误差在5%以内，说明桥梁局部板壳模型能够准确反映桥梁静动力特性，可以用于车致局部振动计算。

表1 杆梁单元模型与局部板壳模型自振特性对比

1.3 加载及求解

采用移动荷载模拟列车过桥，选择宜宾临港长江桥设计车辆CRH3型列车的参数。CRH3型列车单节车辆长度为24.78 m，共有2 个转向架，每个转向架包含2对轮对。列车编组参考实际编组：（动+拖+动+动+动+动+拖+动）×2，共16 节。CRH3型列车车辆定距、轮对轴距、车辆全长分别为8.69、2.50、24.78 m；转向架、轮对、车体质量分别为3.2、2.4、48.0 t。将移动荷载直接作用于桥面板可忽略桥面系对于系统减隔震的影响，计算结果更保守。

根据质量参数，计算得到单个车轮与轨道的集中荷载。根据TB 10002—2017《铁路桥涵设计规范》确定桥梁结构的冲击系数。

基于ANSYS 瞬态分析模块求解列车移动荷载过桥过程的响应，使用ANSYS命令流提取需要的后处理结果。列车每前进0.2 m求解一次。

2 计算结果及分析

2.1 局部振动响应横桥向分布

列车位于线路2 以300 km/h 的车速通过桥梁时，选取跨中以及跨中左右各20 m 截面讨论桥面竖向、横向响应最大值横桥向分布，分别见图2 和图3。图中，x为纵桥向位置，x=60 m 为主跨跨中，x＜ 60 m 为靠近左侧桥塔的截面；y为横桥向位置，y=0为桥梁中心线，线路1 和线路2 位于y＞ 0 的区域。P为曲线峰值。

图2 桥面竖向响应最大值横桥向分布

图3 桥面横向响应最大值横桥向分布

由图2 可知：①列车移动荷载仅在接触位置3 m以内引起了桥面明显的局部弯曲，额外的振动幅值约为1 mm，这一现象与文献［5］的计算结果接近。桥面板在横向发生明显的弯曲，与平截面假定对比，部分区域下挠约1 mm，原因是列车引起的局部振动以及桥梁过宽导致桥面板的刚度较小，导致在自重作用下发生截面内竖向弯曲。越靠近左侧桥塔，截面受到的约束越强，因此截面的扭转幅度更小，靠近列车侧的桥面板（y=10～ 30 m）局部弯曲更加明显，反之亦然。②列车移动荷载作用位置桥面板的速度显著增加，但在8 m 以内速度幅值迅速衰减。三个截面的峰值竖向速度接近，最大速度与距离跨中的位置相关。③加速度规律与速度相似，截面最大加速度出现在车轮接触位置，且加速度随节点位置远离车轮而迅速衰减。各截面最大加速度几乎相同，约为101 m/s2。与速度相比，加速度在-10 m ＜y＜0，8 m ＜y＜15 m 存在较缓的下降平台。

由图3 可知：①桥面板节点的横向位移基本沿桥轴线呈对称分布，但靠近列车的半区响应稍大，原因是桥面的横向位移来源于主梁扭转导致的移动竖向荷载的水平分量，列车荷载作用侧荷载效应更明显。在靠近桥梁中心线的列车作用位置的另外半区（-12 m ＜y＜0），节点的最大值出现了明显的波动，虽然幅度较小，但会影响该区域铁路车辆的轨道不平顺。②横向响应速度与竖向响应速度的规律类似，不同的是，横向响应速度在车轮接触位置的峰值P2、P3两侧，出现了额外的峰值P1和P4。加速度也有类似现象。速度与加速度响应整体沿桥梁中心线呈对称分布。速度在各截面的差异更加明显，加速度节点响应更大。

2.2 局部振动响应纵桥向分布

为分析列车移动荷载过桥对桥面板节点跨向的影响，列车位于线路2 以300 km/h 通过桥梁时提取6 个车道各项响应的最大值。为了避免杆梁单元与板壳单元连接处端部效应对计算结果的影响，仅提取主跨跨中左右各20 m 的梁段进行讨论。竖向、横向响应最大值纵桥向分布分别见图4和图5。

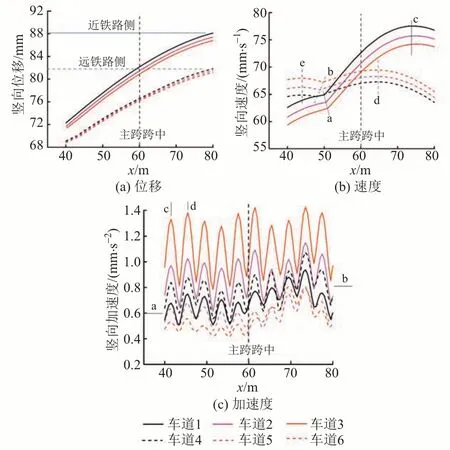
图4 桥面竖向响应最大值纵桥向分布

图5 桥面横向响应最大值纵桥向分布

由图4 可知：①近铁路侧与远铁路侧车道的节点最大位移随纵桥向位置的变化规律类似，均是越靠近左侧桥塔，位移越小。左右两侧车道之间存在较为明显的差异，近铁路侧的车道整体位移较大，与远铁路侧车道位移差从3 mm 增至6 mm，且近铁路侧3 个车道之间的位移差更大。近铁路侧与远铁路侧最大位移的车道不同，近铁路侧是处于外侧的车道1，远铁路侧则是处于内侧的车道4，这一现象是由桥梁的扭转引起的。②车道1—车道3 的速度最大值随纵桥向距离的变化规律相似，车道4—车道6 也有类似的现象，且主跨跨中和左侧桥塔均会对最大竖向速度造成影响。近铁路侧车道随x的增加整体呈上升趋势，仅在c 处存在一个峰值；远铁路侧车道则是在跨中左右两侧d、e处各存在一个峰值。另外，竖向速度随x的变化存在斜率不连续的位置（a、b 处）。这是由桥梁自身振动速度与列车强迫振动速度叠加导致的。越靠近铁路侧的车道竖向速度越大，且出现的位置离跨中越远。③跨中左右两侧的加速度变化比较均衡，加速度随x的变化存在明显的波动且跨中右侧的平衡位置稍高于左侧。各车道峰值出现的位置基本相同，两个波峰间的距离约为4 m，这与主梁横隔板的间距相等。c、d 位置处于两个横隔板的中间，可以认为竖向加速度主要是由列车引起的振动以及横隔板的位置确定。整体而言，越靠近列车线路的车道加速度越大。

由图5 可知：①虽然桥面板各车道横向位移的最大值较小，但车道之间存在较为明显的差距。近铁路侧公路车道间的差别（y1）比远铁路侧（y2）更小，这可能是移动荷载在桥面上的水平分量挤压桥面板造成的，该现象在靠近左侧桥塔的位置更明显。②近铁路侧车道之间的差别很明显，而远铁路侧车道随x的变化规律比较接近。对于近铁路侧车道而言，更靠近列车的车道2以及车道3在跨中两侧均含有2个峰值（车道2 为P2、P3，车道3 为P4、P5），随着车道位置远离列车，两个峰值的位置逐渐接近，最终合成一个（车道1 的P1）。③横向加速度与竖向加速度类似，横向加速度随x的变化具有明显的波动，但波动的平衡位置基本没有变动，越靠近列车的车道，横向加速度越大。

综上，移动荷载引起的竖向响应比横向响应更显著，且距离移动荷载越近，桥面板节点振动越明显。

2.3 列车引起的局部振动对汽车车道的影响

为了进一步分析列车过桥引起的局部振动对附近车道的影响，在列车位于线路1 以300 km/h 通过桥梁时，提取跨中列车轨道处以及车道3 中心节点的竖向响应进行对比，由于速度与加速度变化较为剧烈，仅分析位移，见图6。

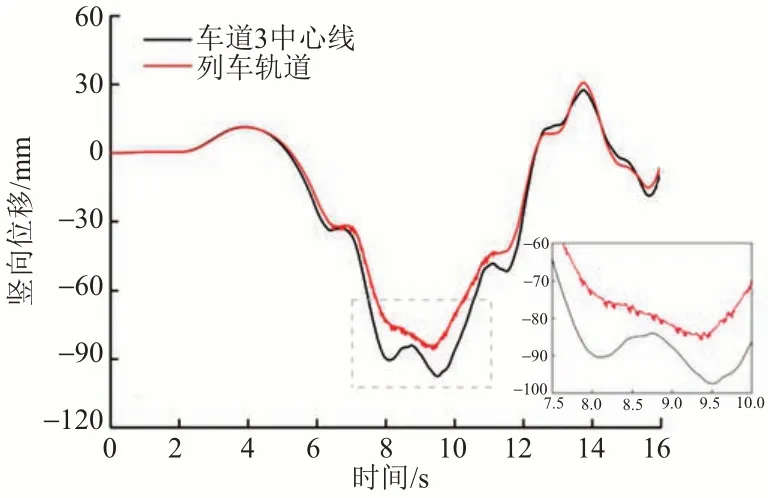
图6 列车轨道与车道3中心线竖向位移时程对比

由图6 可知，车道3 中心线与列车轨道的整体响应趋势接近，这是由桥梁的振动特点决定的。车道3中心线的响应变化比列车轨道的响应变化更快，原因是列车荷载引起的下挠会影响周围的桥面板节点，使得车道3 中心线的响应变化会稍快。在7～ 11 s 时列车荷载直接作用的节点存在剧烈的小幅波动，此时列车正通过跨中，且车道3 中心线有2 个极小值，列车轨道只有1个极小值，原因是桥梁较宽，扭转会引起额外的竖向位移，并与桥梁整体竖向位移叠加。

通过快速傅里叶变换对比车道3中心线以及列车轨道节点竖向响应的频谱，见图7。

图7 车道3中心线与列车轨道功率谱密度对比

由图7 可知：①在车道3 中心线上几乎观察不到桥面板局部振动代表的高频部分。列车轨道节点在30～ 50 Hz仍存在较高的能量，这是由桥面板局部振动引起的，但车道3中心线在10 Hz后已观察不到明显的能量。②车道3中心线与列车轨道均能够观察到与桥梁整体振动相关的低频。车道3中心线与列车轨道仅在桥梁一阶扭转频率的能量上存在明显差异，这是因为两者距离桥梁中心线距离不同，位于更外侧的车道3 中心线具有更强的能量。综上，认为列车荷载引起的局部振动对公路车辆的影响有限。

3 结论

1）列车通过桥梁时，桥梁节点变形与平截面假定相比约有1 mm的误差。

2）列车荷载作用下桥面存在局部振动的情况，竖向响应影响范围约为列车中心线附近5 m 的区域，影响区域的响应较大；横向响应影响范围约为30 m，但影响区域节点响应较小。

3）桥塔的纵向约束、截面与跨中的相对位置以及与横隔板的距离均会影响截面竖向响应的最大值。远离具有纵向约束的桥塔、靠近跨中均会使竖向位移和速度的最大响应增加。远离横隔板会使竖向加速度增加。

4）最靠近列车的车道响应中并未观察到明显的高频成分，且低频部分列车轨道与车道中心线唯一有明显差距的成分来自桥梁的扭转。因此，可以认为荷载列车引起的局部振动对公路车道的影响有限。