基于客货分离的十车道高速公路车道管理适用条件研究

熊文磊，庄稼丰，马天奕

(中交第二公路勘察设计研究院有限公司，湖北 武汉 430056)

伴随我国经济快速发展和综合国力不断提升，各地的交通需求也在飞速增长，交通的再发展已引发了高速公路改扩建的高潮,使得车道数增加、横断面加宽，车辆行驶环境变得更为复杂，这一变化趋势要求我们进一步研究超多车道高速公路的交通运行状态，因地制宜，寻求科学合理的车道管理方案。

国内外已在高速公路车道管理方面进行了大量研究和实践。美国新泽西收费公路拓宽为双向十二车道后，将内侧车道专供小型车行驶，外侧车道供小型车及大型车行驶，大型车优先，并将该路段的立交改造成为客货分离匝道；I-710公路、5号州际公路等货运频繁公路均采用了设置货车专用道的车道管理方式[1]。国内高速公路管理方式的划分依据归纳起来主要有4 种：行驶速度、车型大小、客货车、出口顺序[2]。曹广斌[3]针对某条八车道高速公路的特定交通环境，对比分析了各车道管理方案的优劣；钟小明等[4]针对客货混行车道管理出现的问题，对客货混行、单车道通行、客货分道、错时通行等4种车道管理方式的优缺点和适用条件进行了深入分析；万兵[5]依托西宁至互助公路改扩建工程，应用VISSIM交通仿真软件研究在不同货车混入率的交通状况下，双向六车道高速公路客货分离的自然流量与货车混入率标准。

针对十车道高速公路复杂的交通环境，对车道管理方案的要求更为精细。为了选取合理的车道管理方案，确保扩建后双向十车道高速公路的安全、高效运行，本文以客车、货车为划分依据对4种车道管理方案(无货车禁行车道、左侧一条车道禁行货车、左侧两条车道禁行货车、左侧三条车道禁行货车)进行分析，采用交通模拟仿真技术，通过试验分析交通量、交通组成(货车比例)双重因素对不同车道管理方案带来的影响，提出基于客货分离的十车道高速公路车道管理适用条件，为超多车道高速公路车道管理策略制定提供理论支撑。

1 客货分离必要性

行车安全和效率是评价高速公路交通运行状态的两大核心，而车辆的运行速度是影响二者的关键因素。不同性能、结构的车辆在道路上行驶存在一定的速度差异，是引发交通事故的原因之一[6]。大货车相对于小汽车而言，车型较大且动力性能较低，在行驶的过程中一般表现出速度低、灵活度小以及时空资源消耗大等特征。因此，大车在高速公路上的随意行驶不仅会降低道路的通行能力，其跟驰和超车等行为也会带来较大的安全隐患[7]。

1.1 行车速度影响分析

货车与小客车在外观尺寸、最大动力性能、总质量等参数方面存在较大差异，由实际运营经验可知，两者之间的运行速度也存在较大差异。本研究以广东省某高速车速统计数据为例，对货车与小客车的行车速度进行对比分析，具体数据见表1。

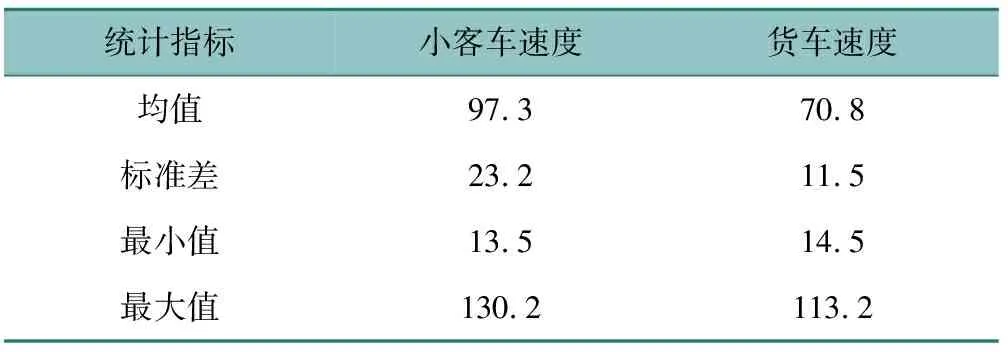
表1 广东省某高速不同车型车速统计表Table 1 Speed statistics of different vehicle types in an expressway in Guangdong Province 单位：km·h-1

从调研数据可知，货车行驶速度与小客车行驶速度之间存在较大差异，小客车整体运行速度高于货车运行速度，且小客车车速标准差较大，表明小客车运行速度不平稳，离散度较高。若不采取车道管理措施，所有车辆在各车道自由混行，跟驰过程中货车的屏障作用会降低小客车的整体运行速度，超车过程中将进一步造成小客车行驶速度离散度增大，行车舒适度及道路安全水平均不理想。

1.2 路段通行能力影响分析

针对客货混行的整体式通行能力，魏雪延等[8]在《公路路线设计规范》(JTG D20—2017)的基础上，考虑内外侧车道间换道影响，提出了更为精细的计算方法，引入fOL表示外侧车道修正系数，fIL表示内侧车道修正系数。具体单向通行能力计算模型表达为

C=CD·fHV·fp·[2fOL+(N-2)·fIL]

,

(1)

式中CD为单车道设计通行能力，N为单向车道数，fp为驾驶人总体特征修正系数，fHV为交通组成修正系数。

针对客货分离式通行能力，因客车与货车分车道行驶，互相影响较小，可单独计算客车道通行能力与货车通行能力，两者之和即为该管理模式下的高速公路通行能力[9]。具体单向通行能力计算模型表达为：

,

(2)

,

(3)

C=Cp+Cf

,

(4)

式中：上标p表示客车道相关参数，上标f表示货车道相关参数。

魏军[10]研究基于VISSIM仿真平台对12车道高速公路各参数进行标定，其中假定fHV=0.65，该研究最终得出两种车道管理方式的通行能力对比如图1所示。

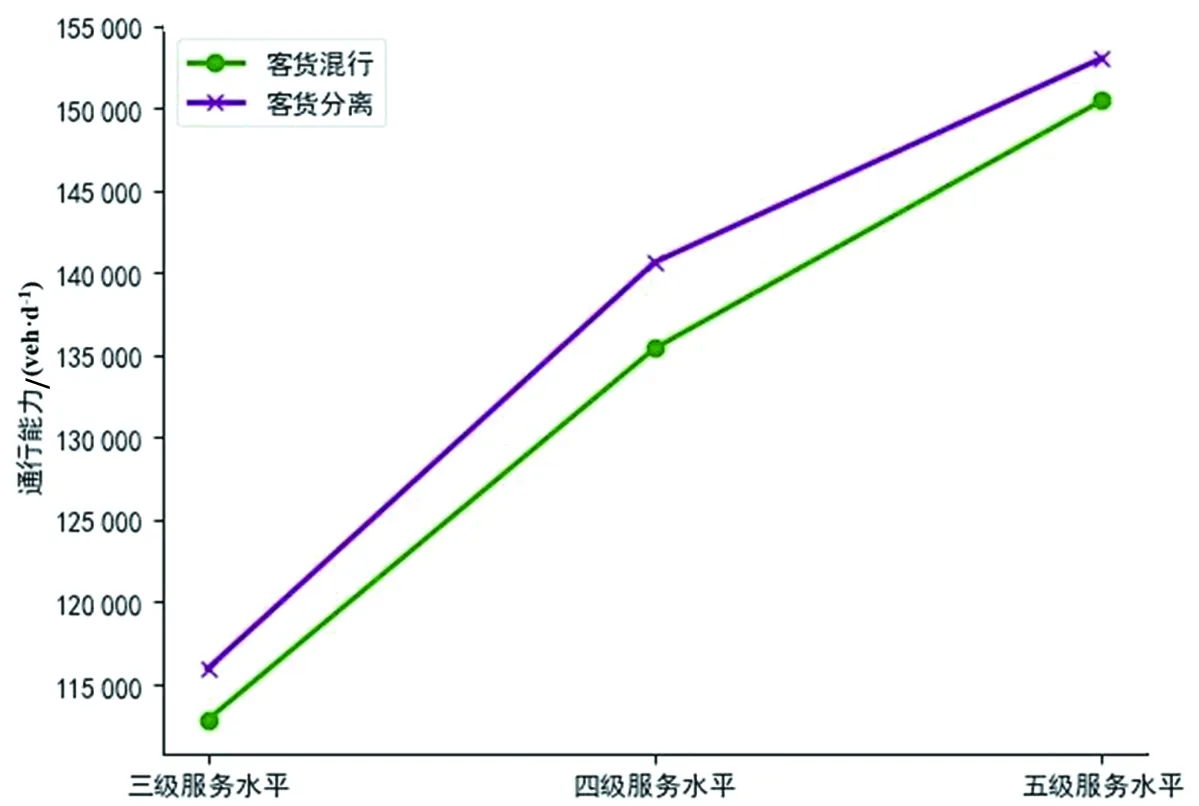
图1 不同车道管理形式下通行能力对比结果Fig.1 Comparison results of traffic capacities with different lane-management forms

由图1可知，针对货车混入率较高的情况，实施客货分离的车道管理方式可以在一定程度上提升路段通行能力。

1.3 行车安全影响分析

裴玉龙等[11]通过对成渝高速、石太高速等高速公路的事故统计数据分析发现，高速公路事故率与行车速度标准差存在极强的数学关系，高速公路行车速度分布离散程度越高，相应的事故率越高。两者的数学关系模型为：

P=9.583 9e0.055 3Δv，

(5)

式中P为事故率(次/(108·车辆数·km))，Δv为车速标准差(km/h)。

由上式可知，高速公路车速标准差与事故率的关系符合指数函数特征，车速标准差的增加将造成事故率指数级增长。因此实施部分车道禁行货车的车道管理方式可有效降低高速公路事故率，对高速公路行车安全具有积极改善意义。

2 基于全面试验设计的交通仿真模型

以客货分离为原则的十车道高速公路车道管理方案可分为无货车禁行车道(不禁行)、左侧一条车道禁行货车(左一禁行)、左侧两条车道禁行货车(左二禁行)、左侧三条车道禁行货车(左三禁行)，4种车道管理方案如图2所示。

图2 基于客货分离的四种车道管理方案示意图Fig.2 Schematic of four lane-management schemes based on passenger and freight separation

为了进一步明确实际工程应用中不同车道管理方案的选择依据，需从运行车速、行车安全、通行能力等方面研究不同车道管理方案的适用条件。受现实条件限制，无法对高速公路不同车道管理方案开展实地测试，故采用虚拟仿真技术验证不同交通条件下的车道管理方案效果。目前主流的交通微观仿真软件为VISSIM，是一种基于时间间隔和驾驶行为的仿真建模工具[12]，其跟驰、换道等驾驶行为采用刺激-反应模型，能够模拟许多城市内和非城市内的交通状况，在同类软件中处于领先地位，本研究试验过程借助VISSIM仿真平台完成。

2.1 评价指标选取

本文主要从行车速度、路段通行能力、行车安全性等方面选取评价指标，作为车道管理策略后评价的重要参数。

平均车速取平均行程速度，可以评价道路的畅通程度，用以衡量交通管理措施的实施效果。对行程速度的调查需要用到行程时间的测定，在仿真模拟时可以借助软件得出，在实际工程中可以借助高速公路收费数据对车辆行程时间的统计数据进行测算，公式如下:

,

(6)

式中vi为第i辆车的行程速度(km/h)，ti为第i辆车的行程时间(h)，s为路段的长度(km)。

(2)通行能力C

通行能力直接反映道路所能承受的交通负荷强度，是车道管理方案后评估的基本参数，本文中关于VISSIM对通行能力的测定方法采用了美国德克萨斯州交通运输协会研究成果[13]，认为高速公路通行能力的取值为拥挤状态下作业区的小时流量。在构建的道路仿真模型作业区后端设置检测点，交通量输入为2 200 pcu/(h·车道数)，将拥挤状态中该检测点的检测数据作为作业区的通行能力值[14]。

(3)冲突数

本文以VISSIM交通仿真中的仿真车辆为对象，利用SSAM软件得出的仿真冲突数作为行车安全评价指标。仿真冲突是指仿真模型中两辆车在相互冲突的轨迹上运行，由于其中一辆车或者两辆车同时采取了避险行为而没有发生仿真事故的事件[15]。运行已搭建好的VISSIM仿真模型，输出仿真车辆轨迹文件，并导入到仿真冲突分析软件SSAM中，即可获得仿真模型中的冲突信息。

2.2 基于VISSIM仿真的全面试验设计

仿真试验拟采取全面试验设计方案，首先根据表2所示交通量、交通组成的取值组合成数量较多的方案，针对不同的取值组合采取四种车道管理方案进行仿真试验，输出路段通行能力、平均车速、冲突数等相应数据，对比不同方案的平均运行车速、路段通行能力以及交通冲突数等指标，分析高速公路路段的运行安全与效率。

表2 全面试验下的双重因素取值表Table 2 Values of double factors with the comprehensive test

值得说明的是，针对试验中各种方案的仿真过程，影响因素中的交通量直接在车辆输入编辑模块设置，仿真时的车辆组成参数由期望车速和大货车比例共同构成，仿真路段长度为2 km。由于微观仿真软件VISSIM中不同的随机种子将改变车辆的达到规律，为了避免随机种子对仿真结果造成的偶然性，仿真时每种试验方案重复运行10次，开展数据分析时采用10次仿真结果的平均值。

2.3 模型参数标定与有效性验证

模型参数标定是指根据仿真对象的交通运行特征对模型中的参数进行调整，达到能够准确模拟仿真对象的实际交通特征的目的。为了验证搭建的VISSIM仿真模型能否客观反映仿真对象的实际交通特征，还需要对模型参数的有效性进行验证。

当前仿真模型参数标定工作已有大量的研究人员开展系列研究，周晨静等[16]以快速路为仿真对象，在Wiedemann99跟车模型默认参数的基础上，以天津市某快速路实测数据为基准，应用遗传算法得到了一定数量的参数标定结果，本研究的仿真试验均采用该参数标定结果，见表3。

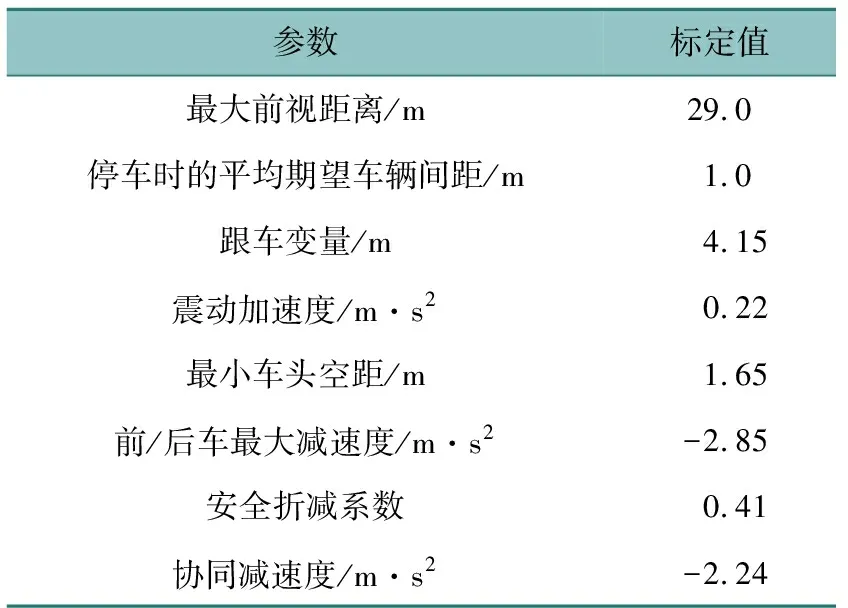
表3 仿真模型参数标定结果Table 3 Calibration results of simulation model parameters

本文获取广东省某高速公路100 m长的实际运营数据，选取道路交通量和车均延误作为校核指标，通过对比仿真模型输出与路段实测的校核指标准确率来反映模型参数的有效性。如表4所示，结果表明，在道路交通量和车均延误两个方面，仿真模型输出的准确率分别为90.2%和91.4%，认为仿真模型能够准确反映仿真对象的实际交通运行状况。

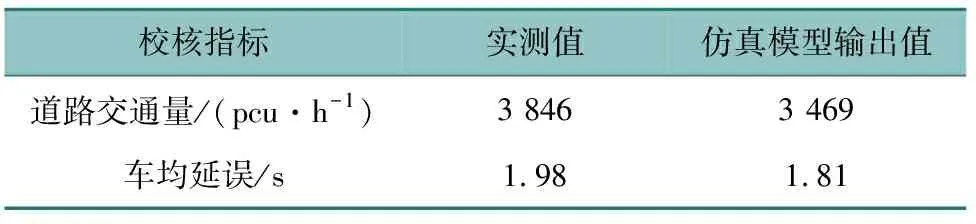
表4 仿真与实测的校核指标结果Table 4 Check index results of simulation and measurement

2.4 仿真结果

共开展117×10组仿真试验，仿真试验结果记录的指标有平均运行车速、道路通行能力及冲突数，以上指标可以较为全面地反映高速公路路段运行效率与运行安全的状况，仿真试验结果数据见OSID科学数据与内容。

以交通量800 pcu/(h·车道数)，货车比例5%条件下仿真结果为例，该交通条件下采取无货车禁行车道(不禁行)的车道管理方式，相较于其他三种车道管理方式，其平均运行车速最高，但冲突数也最高，即各车道管理方案既有优点又有不足，单独对比三个评价指标无法有效评价各车道管理方案的实际效果。因此，为便于综合评价不同车道管理方案下的路段运行水平，需构建车道管理方案的综合评价方法。

3 车道管理适用条件分析

3.1 基于主成分分析法的车道管理方案综合评价方法

利用VISSIM仿真软件，设置多种不同道路交通环境，获取相应道路运行参数，为解决多指标问题对方案评价的影响，需构建车道管理方案的综合评价方法。由于仿真试验记录的不同指标之间存在一定的相关性，如平均运行车速与道路通行能力存在相关性，所以为了化繁为简，抓住关键，解决指标间信息重叠的问题，考虑采用主成分分析法构建车道管理方案综合评价方法。

主成分分析法适用于分析对象的各变量之间存在相关性或变量较多，难以把握变量之间关系的多元统计分析方法。基于主成分分析法的车道管理方案综合评价方法实现过程如下：

①将评价指标平均车速x1、通行能力x2、冲突次数x3的数据标准化。数据标准化可以消除因为指标量纲不同以及数据数值相差过大带来的影响。

,

(7)

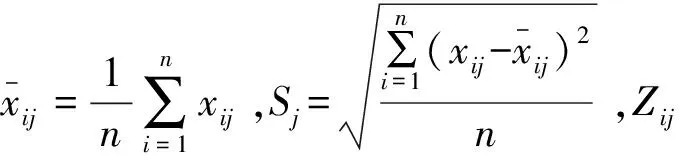
②求出标准化数据的协方差矩阵。

③计算特征根与相应的标准正交特征向量。求出协方差矩阵的特征值，并使其按从大到小的顺序排列：

λ1≥λ2≥λ3≥0

。

(8)

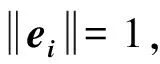
④计算主成分方差贡献率和累积方差贡献率。详见表5。

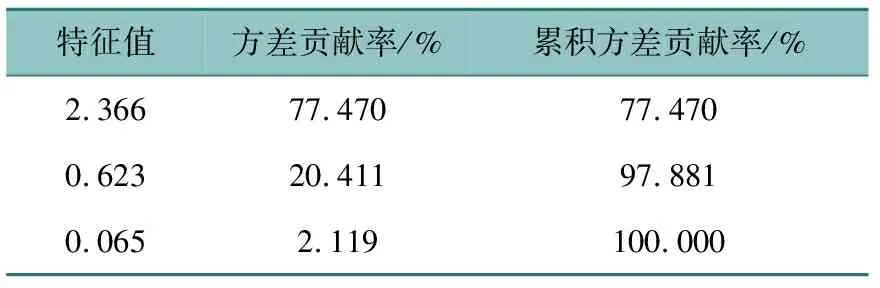
表5 特征值及方差贡献率Table 5 Eigenvalue and variance contribution

⑤确定主成分及表达式。由表6可知，前两个主成分的方差贡献率达到了97%，因此选取前两个主成分即可较好地代替原始指标进行分析。

对应第一个特征值2.366的特征向量为(-0.412，-0.314，0.384),

F1=-0.0.412Z1-0.314Z2+0.384Z3，

(9)

式中Z1、Z2、Z3分别为标准化后的运行车速、通行能力与冲突数，下同。

对应第二个特征值0.623的特征向量为(0.297，-1.095，-0.562),

F2=0.297Z1-1.095Z2-0.562Z3

。

(10)

根据方差解释率对选取的2个主成分进行加权求和即可得到综合得分计算公式：

。

(11)

⑥将计算所得的主成分值进行标准化处理，根据式(11)算出最终车道管理方案综合得分。

3.2 基于综合评分的车道管理方案推荐

根据文中构建的车道管理方案评价方法，对不同交通量与货车比例组合条件下的四种车道管理方案进行综合评价，部分评分结果见表6，全部评分见OSID科学数据与内容。其中，车道管理方案评价得分最高者为相应交通条件下的最优方案。对所有评分结果进行归纳总结，最终得出不同交通量及货车比例下的最优车道管理方案，具体如表7所示。

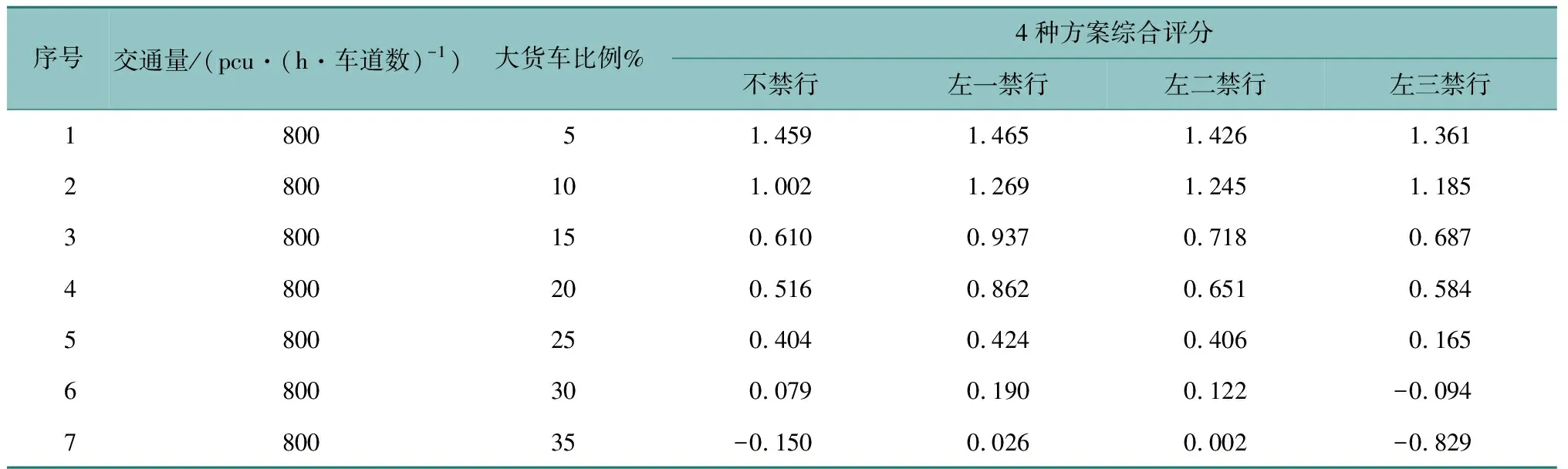
表6 全面试验条件下的不同车道方案综合得分(部分)Table 6 Comprehensive scores of different lane schemes with comprehensive test (part)

表7 不同车道管理方案适用条件Table 7 Conditions applicable for different lane-management schemes

4 结论

通过对交通量及货车比例双重因素影响下的试验仿真结果数据进行分析，综合考虑行车安全、行车速度及路段通行能力等指标变化，根据文中提出的车道管理方案综合评价方法，对117×10组仿真试验数据进行综合评分计算，针对整体式十车道高速公路，得出如下结论：

(1)当交通量≤1 000 pcu/(h·车道数)时，宜在左侧一条车道禁行货车；

(2)当交通量>1 000 pcu/(h·车道数)且货车比例≤30%时，宜在左侧三条车道禁行货车；

(3)当交通量>1 000 pcu/(h·车道数)且货车比例>30%时，宜在左侧两条车道禁行货车。

文中结论依据交通仿真试验结果数据分析得出，可为十车道高速公路运营期的车道管理方案选择提供必要参考。同时，因仿真软件环境与实际行车环境存在一定差异性，因此，需结合各项目实际情况酌情调整。