基于滚动时域控制的轨道交通车站单站限流策略研究

赵庆亮，冯晓斌，吴枫,王一多

(1.北京化工大学 a.经济管理学院;b.数理学院,北京 100029;2.西安交通大学 软件学院，陕西 西安 710049)

城市轨道交通作为城市公共交通的重要组成部分，不仅缓解了城市地面的交通压力，而且对环境保护有着突出的贡献。然而随着城市人口的逐年增加，车站的大客流拥挤情况时常发生，在某一时段车站集中到达的客流量会很大程度地超过车站正常客运设施或客运组织所能承担的流量[1]。客流需求与运输能力的矛盾逐步凸显，部分车站出现乘客滞留站台情况，导致乘客的出行等待时间持续增加[2]。地铁站的拥堵问题不仅对乘客造成困扰，也对列车的运行安全带来很大压力。

针对上述问题很多学者进行了相关研究，孙晟凯等[3]通过构建客流与列车动态交互模型,提出综合评价指数来量化不同客流管控效果。赵鹏等[4]使用线性规划构建车站和时段之间的协调控制模型，通过不同约束进行求解。陈慧等[5]针对车站的大客流拥堵问题，引入客流控制系数，构建系统动力学车站流量模型。Shi等[6]、Yuan等[7]使用整数规划模型优化列车时刻表，以最大程度减少相关车站的乘客候车时间，并设计算法模拟。Xu等[8]提出了一种将连续平均法与遗传算法相结合的算法来求解多站客流分配模型。

另有学者提出使用线路联合调控的方式来限制客流、均衡负载。刘晓华等[9]提出联合客流控制的构想，在高峰时期通过限制上游车站的进入人数来增加负载车站的旅客容量。Xu等[10]、陈锦渠等[11]通过开发基于仿真的统一算法研究了在不确定运力需求时的限流策略，进而为乘客制定出行方案提供依据。Shi等[12]引入了乘客累计风险的概念，通过多线路协同的客流控制来最小化乘客在拥挤情况下的风险。孟凡婷[13]通过构建基于不同评价准则的优化模型,来生成系统最优的客流协同控制策略,从而实现均衡资源配置。

现有研究基本从历史数据入手，并且只是通过单方面优化算法来提高客流运算效率，不能真正地根据站内时间推进考虑客流量的动态变化进行限流优化。因此，本文针对短时大客流引起的站内拥挤问题，通过对乘客出行过程的分析，结合站内安全水平和乘客满意度来构建限流优化模型。同时，提出了基于滚动时域控制的算法，以乘客总延误时间最小为目标，不断计算局部最优限流方案，通过滚动计算得到整体最优解，从而更好地减少站台人数超限次数，有效缩短乘客出行总延误时间。

1 城市轨道交通单站限流优化模型构建

在城市轨道交通网络中，车站作为基本的运载单元，主要由乘客、站台、进站闸机、出站闸机、列车等要素组成，其中站台、进站闸机、出站闸机等固定车站设施属于静态要素，乘客、列车属于流动要素。本文忽略乘客进站前的安检环节、入站闸机进入站台的通道和部分换乘车站的客流流入，将业务流程简化为：乘客通过进站闸机进入车站→乘客进入站台等候列车→列车抵达车站→车内乘客下车进入站台→站台乘客进入车内→乘客从站台前往出站闸机→乘客通过出站闸机离开车站。

1.1 模型条件假设

在现实中，乘客的行为和列车的状态存在很多不可控因素，为了简化模型，减少不可控因素影响及计算复杂度，提高模型的普遍适用性，本文提出如下假设：

(1)列车运行状态正常，严格按照时刻表进行发车，无突发事件或者晚点。

(2)为了线路的安全运营，列车的最大载客流量为定值，即满载率和最大额定载客量的乘积。车内乘客达到最大载客量后乘客停止上车。

(3)乘客到达站台后均匀分布在各车门附近，即乘客进入车厢的概率一定，不存在不同车门位置的上车乘客堆积的问题。

(4)本模型简化换乘车站对于单条线路的影响，只讨论单线车站的情况，换乘流入、流出客流分别被视为本站进入、流出客流。

(5)忽略出站客流对于车站的影响，出站乘客可以被认为是不受任何阻碍的离开车站，对于站台和通道的影响微乎其微。

(6)为简化计算，入站客流的速度被认为是常数，即入站乘客以一定的速度进入车站。不存在短时间内大量乘客进入车站导致的客流峰值。

(7)排除由于乘客主观因素或是突发事件等造成的影响通行效率的相关因素。

1.2 目标函数

在高峰期时，部分瓶颈节点的运力基本都已经饱和，站台上开始出现乘客滞留的现象，等待时间包括乘客在站台上的等待时间和因为限流措施导致的在站外或是其他引流位置等待的时间，即：

Tdelay=Tplatform+Tqueue，

(1)

式中Tdelay为总乘客等待时间，Tplatform为乘客在站台上等待时间，Tqueue为乘客在其他引流位置的等待时间。

乘客在站台上的等待时间又可分为乘客正常的候车时间和由于列车容量限制无法上车而需要等待下一趟列车的等待时间。公式如下：

(2)

式中,Δt为列车发车间隔时间，在列车发车间隔确定以及乘客到达呈均匀分布时，乘客的平均等待时间为列车发车间隔的一半；Qpt1为由于列车未到站而导致站台上等待的人数；Qpt2为由于列车满员而没有上车的人数。

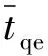
(3)

同时，需要对不同区域的等待时间设置等待系数。对车站管理部门来说，为降低安全事故风险，希望站台内的乘客数量能够保持低于满载的状态，即乘客滞留在站外，而不是在站台上等待。对于乘客来说，由于当天天气等各方面因素的影响，在站外排队会大大降低满意度。因此，本模型针对限流区域的等待时间和因列车满载而需要等待后续列车的等待时间设置了不同的补偿系数θ1和θ2。

Tdelay=θ1Tplatform+θ2Tqueue

。

(4)

根据以上分析，将模型设置的公式(1)～(4)进行联立，可得该模型的目标函数为:

(5)

该模型以乘客总延误时间最小为目标，通过控制车站内的限流人数和站台人数，改善站点内各处拥挤的情况。随着限流策略影响到的乘客人数增加，乘客在站外的等候时间会加长，但是进站乘客和站点内部的乘客会减少，出现乘客未能上车的几率就会下降，同时也能为下游车站留出运力富余的空间。

1.3 模型约束条件

本文提出的单站限流模型是根据车站的实际情况，发现制约车站承载能力的服务设施主要是站台和列车，其余的设施如进站通道等对于车站内客流流速影响有限。因此，本模型的约束条件主要集中在站台和列车的承载能力及限流区域情况。

1.3.1 站台容量约束

在一段时间内站台的承载人数并不是无限的，在不考虑下车人数对于站台的影响后，站台上的人数需要符合以下约束。

(6)

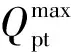
在车站正常运行时，站台上的人数变化存在两种状态，一种是列车未到站，乘客在站台上等待列车；另一种是列车到站，乘客进行上下车行为。为辅助说明，本模型引入变量T(t)来说明站台的状态：当T(t)=1时，说明列车正停靠在车站内，乘客正在上下车；当T(t)=0时，列车未抵达该车站，站台上乘客正在候车。其中，t=0,1,2，…，N，对应全天列车编次。

(7)

(1)列车未到达车站时站台上的乘客人数

在列车未到达车站时，站台上的乘客数量由原本由于列车满员没有上车的乘客加上从进站闸机进入站台的新乘客，公式如下：

∃T(t)=0，

Qpt(t)=Qpt2(t-1)+ΔQpt1(t)，

(8)

式中Qpt(t)为t时刻的站台上人数，ΔQpt1(t)为t时刻通过限流区域进入进站闸机后到达站台的人数。

(2)列车停靠车站时站台上的乘客人数

在列车到达车站后，原本站台上等待的乘客开始上车，直到站台清空或是列车满载，同时，通过限流措施的乘客继续进入站台，公式如下：

∃T(t)=1，

Qpt(t)=Qpt2(t-1)+ΔQpt1(t)-Qin(t)，

(9)

式中，Qin(t)为从站台进入车厢的乘客人数。

每次列车发车后还需要计算一次站台上留存的乘客人数，即在列车发车时，站台总人数减去上车的人数，在列车运力满足该站点的客流需求的时候，站台的留存人数为0，所有乘客都能够上车，具体公式如下：

∃T(t)=1，

Qpt2=Qpt(t)-Qin(t)。

(10)

1.3.2 列车容量约束

在列车的正常运营过程中，乘客的数量一般不会达到列车容量，站台上乘客都能上车，但在高峰时段内，可能存在本站上车的人数过多而导致列车满载的情况，此时站台上候车乘客需要等待下一趟列车，直到列车的运力有剩余为止。因此，在t时刻能够上车的乘客数量即为站台人数和列车剩余运力的最小值：

(11)

式中Qpt(t)为站台上人数，T(t)为此时列车状态，θmax为列车的满载率，C为列车的最大载客人数，Qtrain(t)为t时刻列车内人数。

由于管理部门一般不会让列车满载，而是将车内乘客控制在一定比率下，防止安全事故的发生，因此列车内的乘客上限即为：

(12)

列车内的乘客数量为线路中上游车站上车的累计净人数，减去本站下车的人数，其人数之差应该不大于列车内的乘客上限。即：

(13)

(14)

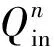
1.3.3 限流区域约束

由于进站口采用了限流的方式来控制客流，在t时刻会有一些在原本条件下能够进入车站的乘客未能进入车站，这样的乘客即为被限流的乘客。进站的乘客就被抽象为进站人数加上某时刻之前被限流的人数，最后减去被限流的乘客人数，

ΔQpt1(t)=Qe(t)+Qqe(t-1)-Qqe(t)，

(15)

式中ΔQpt1(t)为通过限流措施到达站台的人数，Qe(t)为t时刻到达车站的人数，Qqe(t)为t时刻被限流的乘客人数。

同时限流人数也不能大于此时在进站口等待的总人数，

Qqe≤Qe(t)+Qqe(t-1)

。

(16)

2 基于滚动时域控制的限流模型计算方法

由于城市地铁系统的客流数据具有时变性，传统的静态数据计算不能即时地反应和处理车站调度与控制上的问题。本文以乘客总延误时间最小为目标，引入滚动时域控制的思想[14-15]，每个时间段中的系统状态都通过求解一个带约束的优化问题来固定，对每个细分时段都进行优化计算，并将得到的结果作为参数带入下一次计算，不断迭代决策，最终得到动态的优化限流方案。

2.1 算法流程

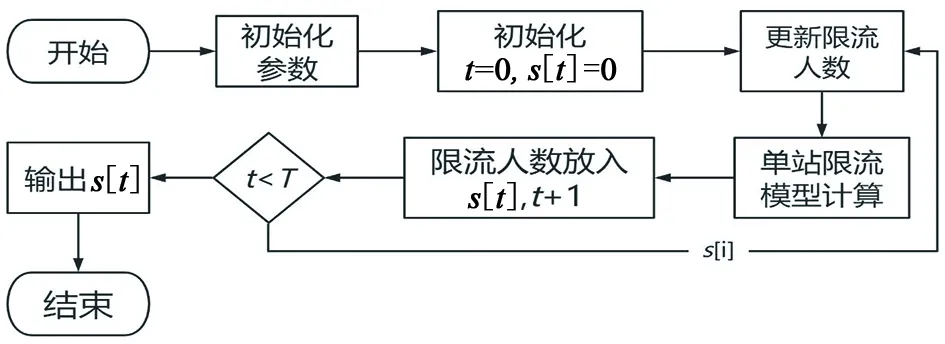
图1 算法流程图Fig.1 Algorithm flowchart

将整个需要限流时段的总时间设为T，将总时间分成多个等长的决策时段TD，系统开始迭代的时刻为t0。算法开始工作后，需要计算每个决策时段中的限流乘客人数，即[t0,t0+TD]时段中的限流策略，此时需要将模型的参数如站台容量、乘客流量等输入模型进行计算，模型会得出该时段中的最优解，并自动判断此时是否需要限流。完成初次迭代后，系统会将得到的结果保存在滚动系数s[t]变量中，并使用得到的策略来计算下一时段[t0+TD,t0+2TD]的系统状态。不断重复上述过程，直到所有的决策时段中的滚动变量都被计算完毕，输出车站在整个限流时段中的限流策略。算法的流程图见图1。

本文主要使用Python中的Scipy库和Numpy库来进行单站限流优化模型的实现，可以方便解决非线性和线性规划问题(支持全局最优解和局部最优解)，寻根和曲线拟合，通过Scipy库中minimize函数来寻找全局最优解，并将最优解放入限流策略中，不断迭代计算过程，得到最终结果。

2.2 模型参数选择

本文设置上午7:00为限流开始时间，在合理假设的情况下设定相关参数如下：

(1)列车到站的时间不存在晚点的情况，每辆列车到站的时间间隔为3 min。开始时刻为一趟列车刚好离开该站的下一时刻。

(2)列车的最大载客人数为500人/列。

(3)为了控制列车内人数，保证线路的正常运营和乘客体验，列车满载率控制在0.9。

(4)到达车站时，列车的满载率控制在0.4～0.6。本模型只讨论单线车站的情况，换乘流入客流被视为本站进入客流，换出客流被视为本站流出客流，以列车内最小和最大限制容量为标准，到达站台时列车上的人数根据列车对应满载率在系统中生成。

(5)乘客到达车站是一个连续均匀到达的过程。为简化计算，可近似认为到达车站人数为固定值，为100人/min，初始时段进入人数也为如此。

表1 相关参数表Table 1 Related parameters

对乘客在站外因限流而等待时间的惩罚系数θ1设置为1.1，在站台等待时间的惩罚系数θ2设置为1.2。

2.3 系统计算结果与分析

将上文中设置完成的参数导入程序进行计算，并将结果进行对比，即仅考虑站台最大容量限制的限流策略，在站台人数达到最大承载数量时，将后面进入的乘客引导进入限流区域，减缓进站时间，等效于停止站外旅客进入站内，减缓站内拥挤。计算两种策略的优化函数值和不同时段的站台内人数。

在假设案例中，系统求解出的结果为[t,1]的稀疏矩阵，不利于展示，本文将其分为6个时段，每个时段10 min。结果如图2所示。

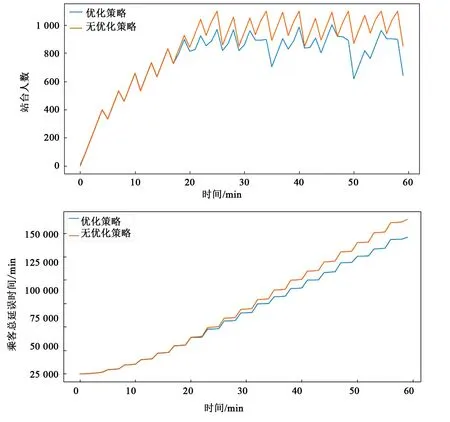
图2 两种策略下站台人数和乘客总体延误时间Fig.2 Number of people on a platform and the total delay time of passengers under the two strategies

因此，通过计算模型及结果分析，可以得到在使用优化限流策略前后的指标数据对比，见表2。

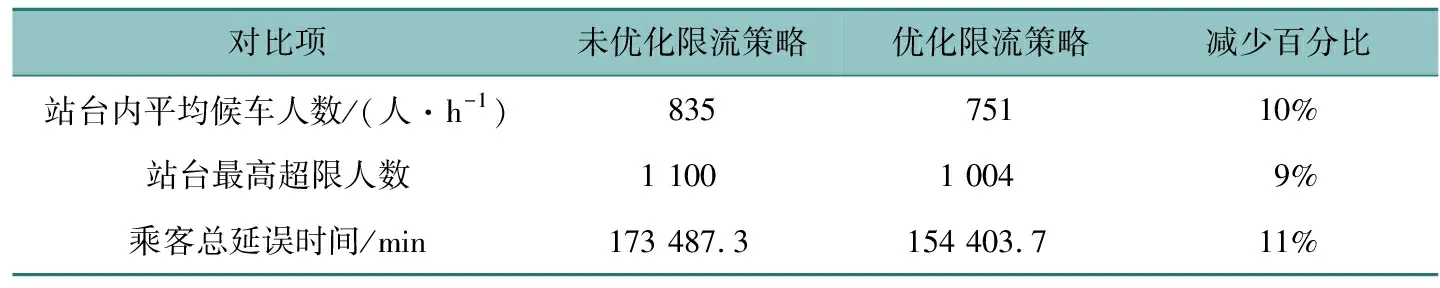
表2 限流前后指标对比Table 2 Comparison of indicators before and after traffic restriction

因而，通过图2和表2中的结果分析可以得出，采用动态限流策略后，乘客总延误时间从173 487.3 min降低到了154 403.7 min，减少约11%。并且看到，在20 min左右两策略出现分歧，正是站台人数达到阈值、车站运行处于拥挤的时间点。之后随着时间的推移，优化效果更佳，说明策略在车站处于拥挤状态时具有良好效果。

另外，动态限流策略也有效降低了站台内的候车人数，从平均835人/h降低到751人/h，降低了约10%。同时，策略也减少了站台超限人数的时刻，站台人数超限的情况由19次降低到了1次，而且超限人数从最高的1 100人下降到了1 004人，说明该策略能够有效减少站台拥挤的情况，并减少了大量因为列车满员而无法上车并在站台上继续等待的乘客，提高了乘客满意度。

从限流人数来看，动态优化后的限流人数明显增加，并且在人数未达到阈值时也进行了小规模的限流，延迟了站内乘客数量高峰的出现。在限流时段较长的情况下，被限流的乘客也只是延缓了进入站台的时间，而动态优化策略更早地进行站外限流，在后续的阶段仍可正常进站乘车。

3 结论

本文针对轨道交通网络的高负载节点存在的站台拥挤问题，在考虑站内安全问题和乘客满意度的两个角度下，建立数学模型优化乘客的平均等待时间，并基于滚动时域控制设计了限流模型的计算方法。实验结果表明，使用该动态限流策略，可使站台的最高超限人数减少约9%，保证了站台的安全性；另外有效降低了出行乘客的总延误时间约11%，并且能够在客流高峰时期有效减少站台的超限次数，即站台人数超过站台容量限制的次数在逐渐减少。因此，该模型和算法的有效性可以得到很好地证实，能够为城市轨道交通限流提供有效参考。

本文中模型简化了换乘车站对于单条线路的影响，未考虑到换乘客流的到达规律。在未来应当从单站限流优化拓展到多站协同限流优化方案，结合乘客画像充分考虑换乘客流的特点并加入至模型，以提出更具有普遍意义的多目标优化方案。