深度教学理念下实数指数幂教学之探究

李晶晶 李 芹 陆立伟

(1.江苏省盐城市特殊教育中等专业学校 224000；2.江苏省盐城特殊教育学校 224000)

当今社会正处于知识爆炸的年代，我们汲取知识的速度往往难以赶上知识更替的频率，这就要求我们要学会学习，学会深度学习，用有限的时间获取最大限量的知识.“深度教学”要求我们必须超越具体知识和技能，深入到思维的层面实现思维品质的提升，帮助学生学会学习，进行有效地学习.因而，数学教师在数学课堂教学中，应当借助设置阶梯型、体验型、合作型、反思型等能够让学生走向“最近发展区”的问题，激发学生理解数学知识、求证数学结论的好奇心，提升学生数学认知水平，促进学生数学高阶思维的提升与发展.

在具体的教学中，我发现中职《数学》(第一册)中第四章第1节《实数指数幂》的教材内容比较琐碎和复杂，使用起来不够方便.对此，我特地做了一些思考和研究，认为从知识的拓展与重建方面入手，或许更有助于知识的学习和理解.下面作简单说明.

1 由简到繁捋求知路，类比拓展见新思维

深度教学不是拔高教学难度，而是引导学生充分思考、发展学习能力的教学.深度教学的实现离不开学生的参与.授课时教师要立足于深度教学的内涵和特点，以学生为中心，引入数学思想方法，渗透数学文化内容，通过迁移经验让学生深入理解基础知识，掌握学习方法，激发学习兴趣，提高学习效果.

处于中职学段的学生都有着“数的拓展”的学习经历，如图1所示，重新整理一下如图2所示.经过拓展以后，学生的认知结构中关于数的知识框架如图3所示.

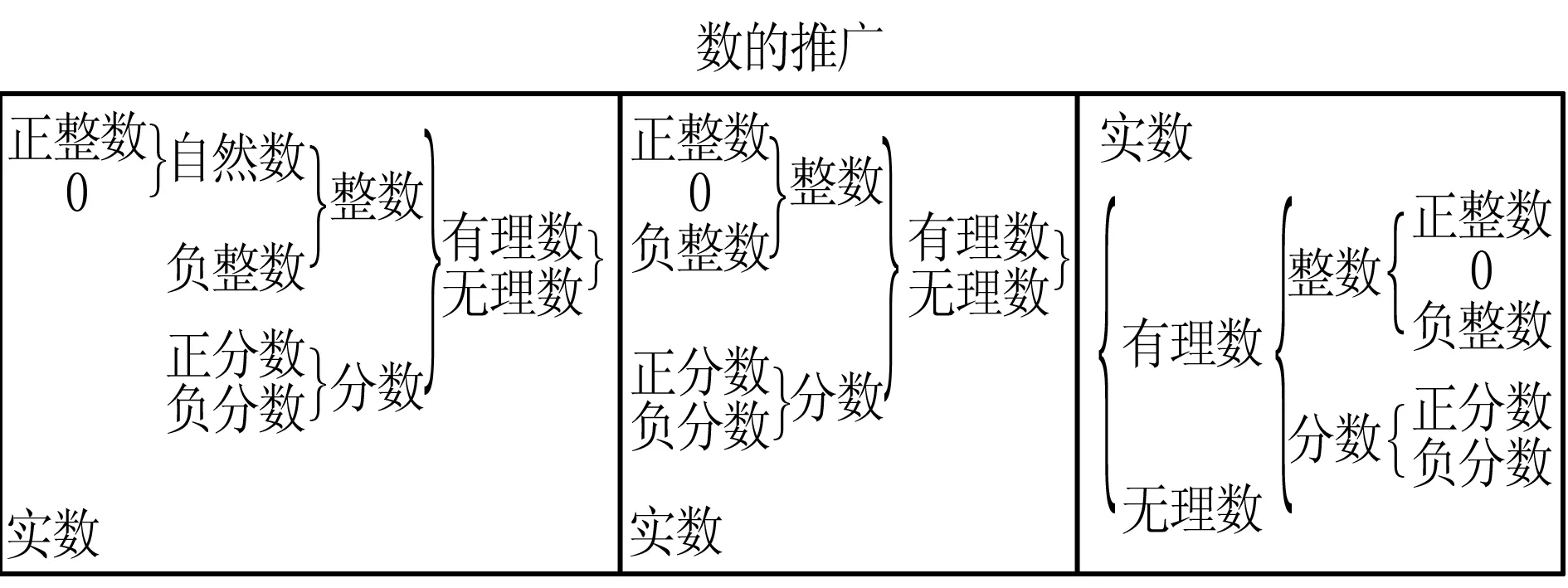
图1 图2 图3

关于指数幂，中职学生的数学学习基础是整数指数幂，部分基础薄弱的学生的现有数学学习基础只是正整数指数幂.鉴于上面“数的拓展”，结合学生的现有数学基础，数学教师可以尝试引导学生利用类比迁移的方法将(正)整数指数幂进行推广或拓展为分数指数幂乃至有理数指数幂，进而推广拓展到实数指数幂，如图4所示.

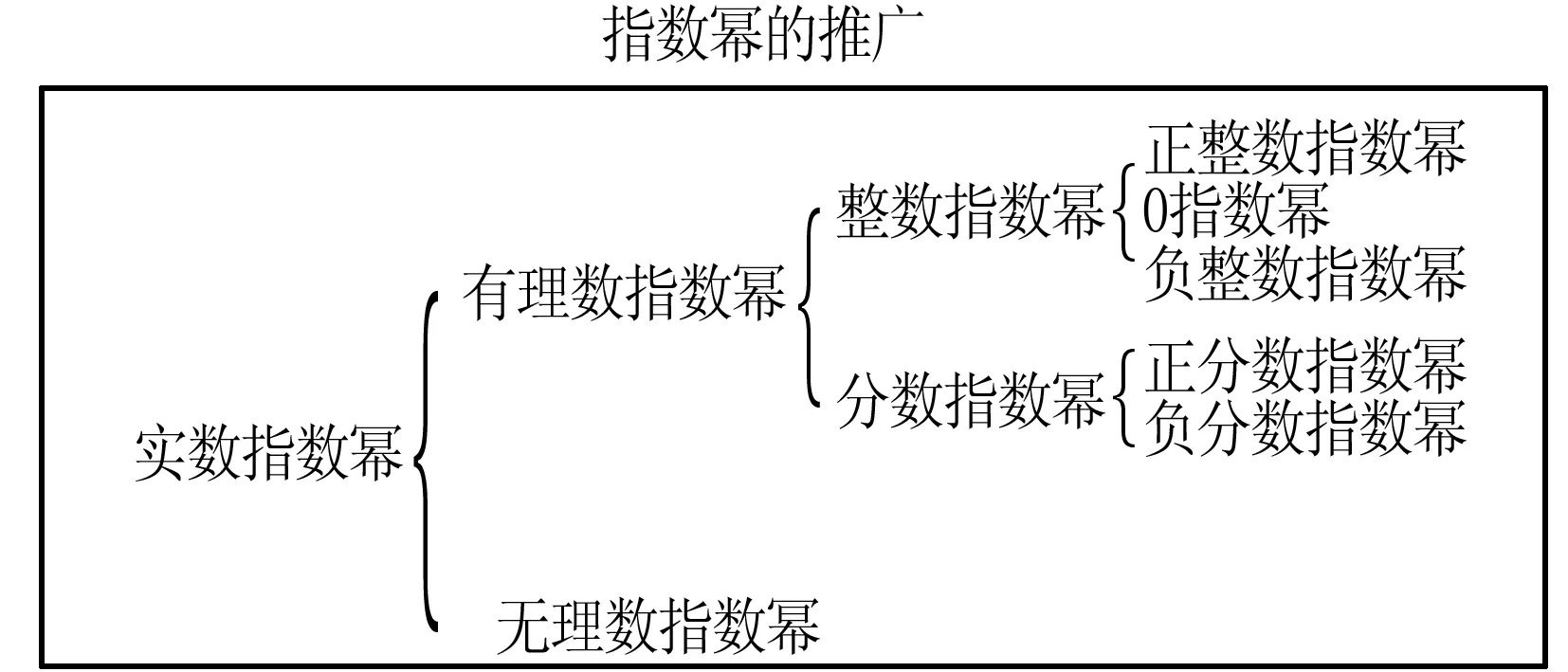
图4

2 精准复习固旧知识，深度学习练新体会

首先，引导学生回忆整数指数幂的运算规则.

2.1 整数指数幂运算规则(分类记忆)

am·an=am+n

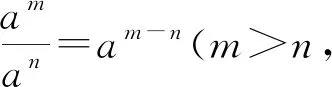
(am)n=amn

(ab)m=am·bm

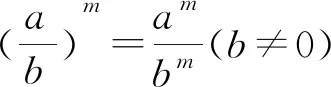
大部分学生可能只能回忆起前两个公式，后面三个公式可能会有点混乱.此时，数学老师可以引导学生给公式起名并分类，引导学生仔细观察，充分归类.采用分类记忆法重新构建整数指数幂知识树，见表1.

表1

2.2 整数指数幂(深度复习)

深度教学不仅仅是要求学生记住公式，还要让学生懂得公式的来龙去脉，懂得如何推导公式，哪怕有一天公式忘记了，能够根据公式推导原理随时推导公式.

为了研究的方便，此处将整数指数幂分为指数为正整数、0、负整数的指数幂，并分别取名为“正整数指数幂”“零指数幂”和“负整数指数幂”.下面从深度教学的角度逐一讲解.

2.2.1 正整数指数幂

2.2.2 零指数幂

零指数幂即a0=1，此项可以省略不研究，或者直接归结到“正整数指数幂”行列.

2.2.3 负整数指数幂

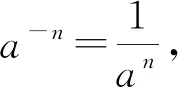
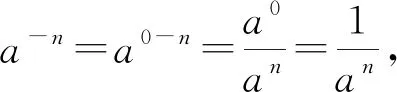
(负整数指数“转化为” 正整数指数)

3 类比迁移探新问题，深度教学化新认知

根据数的拓展知识，复习完整数指数幂，自然而然就会想到分数指数幂.采用同样的方法，以指数的正负进行分类，将指数幂分为指数为正、负的指数幂，并命名为“正分数指数幂”和“负分数指数幂”，如下所示.

3.1 分数指数幂

对于正分数指数幂和负分数指数幂的学习，我们同样不能只满足于记忆公式，而是要懂得公式的来源与推导过程.接下来我们逐一推导.

3.2 正分数指数幂

【公式推导】

推导依据：幂的乘方运算

思想方法：转化思想、整体思想、设元思想

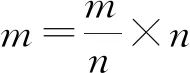
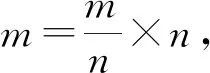
【反思】授人以鱼不如授人以渔，要教会学生学会思考，学会用已有知识解决未知问题，即化未知为已知.帮助学生建立起知识树，懂得知识原理，懂得溯源，懂得使用的数学思想方法，学会归纳总结，实现有意义学习.

3.3 负分数指数幂

【公式推导】

推导依据：同底数幂相除

思想方法：转化思想、整体思想、设元思想、发散思维

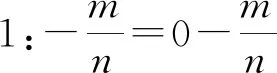
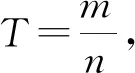
4 整合归纳建知识树，新旧衔接强干枝叶

4.1 有理数指数幂与实数指数幂

通过上面的探究学习，我们可以很容易地将整数指数幂拓展到有理数指数幂，如图5所示.

图5

在有理数指数幂的基础上做进一步的推广与拓展，将得到实数指数幂，如图6所示.

4.2 实数指数幂运算规则

对整数指数幂运算规则作进一步推广，将得到实数指数幂运算规则，并重新做归纳分类，如表2.

表2

总之，教师应该充分利用学生的现有学习基础，利用联系、迁移、转化等方法，尽可能创造“最近发展区”，充分调动学生的学习积极性，帮助学生学会化未知为已知，用已有的知识解决未知的问题.引导学生构建自己的知识树，拓展知识、丰富知识，在教师深度教学的基础上实现学生的深度学习.