高中数学解题中化归思想的应用
张侠飞
(安徽省亳州市第三十二中学 236800)
1 化归思想之换元转化
换元转化是非常常用的化归方法.在遇到数学式较为复杂,不易找到数学式之间的内在联系时常使用换元转化.通过换元转化可使数学式子变得简洁,更容易构建与其他数学知识点之间的内在联系,帮助学习者尽快地找到解题思路.实践表明,换元转化的方法较多,主要分为整体换元、三角换元、均值换元等,其中前两种换元方法应用广泛,尤其在解答三角函数类的习题中可获得意想不到的效果.但需要注意部分习题并不能直接判断是否需要进行换元转化,需运用所学数学知识对已知条件进行整理,在整理过程中应具备换元转化意识.换元转化的关键在于保证换元前后取值范围的一致性,这一点应引起足够重视.
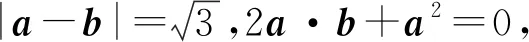
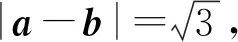
2 化归思想之构造转化
运用化归思想解题的方法多种多样,其中构造转化是化归思想的重要代表.构造转化指基于对相关参数关系的本质理解,运用所学数学知识构建新的逻辑关系,化陌生为熟悉,从而更好地运用所学知识解决问题.由此可知构造转化的难点在于:其一,如何通过构造将新的问题转化为熟悉的问题.解题时需认真观察所给数学式子的特点,找到共同点,为构造做准备.同时,积极联系熟悉的知识点,建立与所学数学知识的联系,完成构造.其二,构造后的处理.构造的目的在于更好地处理问题,因此,构造后应明确如何处理构造出的新关系.
例2已知a=e0.1-1,b=sin0.1,c=ln1.1,则( ).
A.a 数形转化是高中数学解题中较为常用的化归方法.众所周知,数和形在本质上具有统一性,通过数形之间的转化可创造性地解决数学问题.研究发现,数形转化常被用于解答函数零点、方程根的个数以及与分段函数相关的恒成立问题.运用数形转化解题时应注意把握以下关键环节:其一,如何画出正确的函数图像.其二,如何分析出关键位置.找到图像的关键位置是解题的关键,尤其在难以直观判断出相关位置时应大胆设出参数,运用所学求出对应参数. 图1 直接转化是解答高中数学习题时又一常用的化归方法.因高中数学习题情境以及考查的知识点不同,因此,运用直接转化解题的难度存在一定差别.部分习题运用所学知识或解题经验即可完成由陌生到熟悉的转化.而部分习题则需学习者具备较强的抽象、概括能力.为确保能运用直接转化顺利解答相关习题,一方面,要保证转化的等价性.另一方面,转化时最容易在参数取值范围上出错,尤其涉及到不等式问题时很多学习者常将不等式的符号搞错,因此,转化时应保证推理的严谨性,严格按照不等式性质进行推理. 坐标转化常用于解答高中数学中较为复杂的图形类问题,尤其用于解答立体几何习题可获得显著效果.为保证转化后运算的高效性,构建合理的空间直角坐标系是关键.一般情况下应注重运用已知条件中的垂直关系构建空间直角坐标系.针对未给出垂直关系的情况,还应运用几何图形性质做出相关辅助线.另外,完成空间直角坐标系的构建后应注重运用几何图形性质、三角函数、正弦定理、余弦定理等求出相关线段长度,以确定对应点的空间坐标,并灵活运用向量运算,求出最终结果. 例5如图2,已知三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC和△BCD均为等腰直角三角形,其中∠BAC=∠BCD=90°,BC=2,点P为线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ和AC成30°的角,则线段PA长的取值范围为____. 图2 图3
3 化归思想之数形转化
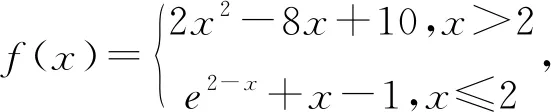



4 化归思想之直接转化


5 化归思想之坐标转化