考虑水化学损伤的岩石真三轴蠕变本构模型1)
陈有亮 陈奇键 肖鹏 杜 曦† 王苏然*
* (上海理工大学环境与建筑学院土木工程系,上海 200093)
† (亚琛工业大学工程地质与水文地质系,德国亚琛52064)
** (东南大学交通学院,南京 210096)
†† (新南威尔士大学土木与环境工程学院,澳大利亚悉尼 2052)
*** (同济大学地下建筑与工程系,上海 200093)
引言
岩石流变是岩石力学性质随时间变化的行为,包括蠕变、松弛、弹性后效等流变特性,与岩石工程的长期稳定性和安全息息相关,大量工程实践与理论研究表明[1-3],许多岩石工程的破坏与失稳都是发生在工程运营期间,由于岩石流变而导致的工程破坏与所带来的财产生命损失往往十分重大,因此,研究岩石的流变本构模型对实际工程的稳定与安全具有重要的理论意义.近年来,在岩石蠕变本构模型的推导与建立方面已经取得了不少阶段性的成果:刘东燕等[4]对重庆地区的砂岩进行了不同围压下的蠕变试验,将优化后的Kelvin 与Burgers 模型串联,得到可体现加速蠕变特征的非线性蠕变模型,基于试验数据,采用1 stOpt 软件的全局优化算法,进行模型参数识别后得到合理的结果.刘文博等[5]对取自阜新恒大煤矿深部的围岩开展了室内三轴蠕变试验,分析岩石的蠕变变形规律,并基于经典的蠕变元件,得到一种能反应非线性加速蠕变阶段的本构模型,并用试验数据进行了验证.张向东等[6]通过引入西原体和Kachanov 损伤模型,建立能描述加速蠕变阶段的损伤蠕变模型,并进行砂岩在分级荷载作用下的三轴蠕变试验,用试验的数据对建立的蠕变本构模型进行了验证.刘文博等[7]对Kelvin模型进行了改进,进而构建可反映岩石加速蠕变变形特征的弹塑性损伤蠕变模型,并提出一种确定蠕变模型参数的方法.韩阳等[8]建立了一种非定常伯格斯岩石蠕变模型,并与传统的伯格斯模型进行对比,可以反应岩石蠕变的3 个阶段.张亮亮等[9]指出前人研究中对蠕变模型建立过程中与参数辨识的不严谨之处,并建立一个能同时描述岩石蠕变过程中的瞬时弹性应变、衰减蠕变、等速蠕变和加速蠕变阶段的本构模型.
上述学者建立的岩石蠕变模型都是在单轴或常规三轴的条件下得到的,而针对真三轴应力状态下的岩石蠕变本构的研究还比较缺乏.实际的工程中岩石往往处于三相应力的状态,中间主应力的存在会显著影响岩石的瞬时和时效力学特性.
同时,岩石赋存的环境往往是复杂且多变的,如我国的西南四川盆地酸雨区,岩石所处的酸性环境会对岩石工程的力学性质产生影响: 酸性溶液中含有的化学成分与岩石发生反应,改变岩石的微观结构,降低岩石的承载能力,许多学者研究表明[10-15],化学溶液对岩石的损伤发展和力学性能有着重大的影响,不过这些成果多是针对岩石的瞬时力学特性,包括岩石的室内试验与模型的建立,而对岩石在化学腐蚀作用下的蠕变特性的研究比较少见.
因此,为了研究岩石在酸性环境与真三轴应力情况下的时效性特征,准确描述岩石在酸性环境与真三轴应力共同作用下蠕变行为的各阶段特征,基于水岩作用的化学动力学理论,定义了考虑PH 值与时间的化学损伤因子,将弹性体,非线性Kelvin体,线性Kelvin 体,黏弹塑性体进行串联,并考虑岩石在真三轴应力作用下的实际情况,建立考虑岩石酸腐与真三轴应力耦合作用下的损伤蠕变本构模型,并用已有的试验研究数据对推导的模型进行参数辨识与验证,通过数据拟合得到岩石在真三轴应力下的屈服面方程,探讨了中间主应力对蠕变模型的影响,结果表明: 推导的本构模型能很好的反应岩石在水化学环境下的真三轴蠕变特性,具有一定的合理性与实用性.
1 非线性化学损伤真三轴蠕变模型的建立
1.1 损伤分析
当工程的岩石处于酸性环境中时,一方面岩石受到荷载的作用形成应力损伤,另一方面酸性环境中的化学成分与岩石发生反应,使得岩石内部的胶结物溶蚀,从而使孔隙增大,微裂缝延展,形成化学损伤.岩石内部的微裂缝的发展与贯通体现了岩石的损伤,姜立春等[16]通过定义岩石的基准损伤状态,将Lemaitre 应变等效原理进行了改进,岩石受到外力F的作用,损伤产生扩展,取其中的两种损伤状态,对于处在酸性环境中的岩石材料,岩石在酸性损伤状态下的有效应力作用于酸性和应力共同损伤状态引起的应变等价于岩石在酸性和应力共同损伤状态下的有效应力作用于酸性损伤状态下的应变,即
式中,σ1和E1为岩石在酸性损伤状态下的有效应力和弹性模量,σ2和E2为岩石在酸性损伤和应力损伤共同状态下的有效应力和弹性模量.
因此可以进行下一步的推导过程,首先根据Lemaitre 应变等效原理得到
式中,Dc为化学腐蚀造成的化学损伤,E0为岩石初始弹性模量.
然后根据改进后的Lemaitre 应变等效原理得到
式中,Dm为应力加载造成的应力损伤.
将式(2)代入到式(3)得
所以有 (1−Dm)(1−Dc)=1−Dcm,即
式中,Dcm为化学腐蚀和应力加载造成的应力总损伤.
1.1.1 考虑pH 值和时间的化学损伤变量
Li 等[17]提出的基于细观结构的损伤变量可以表示为如下形式
式中,ΔSt为经过时间t之后岩石颗粒间减少的接触面积,S0为初始时刻岩石颗粒间的接触面积;Δωt为经过时间t之后岩石之间已溶胶结物的摩尔数,ω0为初始时刻可溶胶结物的摩尔数.
岩石与酸性溶液发生反应的本质是岩石中的物质与H+离子发生化学反应,溶液里H+消耗的快慢反映了溶液里各个化学反应的综合反应速率,H+离子综合反应速率表达式如下
式中,比例常数p为综合反应速率参数,x0为离子浓度参数.
其次,根据pH 值与H+浓度的关系
并结合初始条件求解微分方程得到
式中,pH(t) 和pH0分别表示某时刻化学溶液的pH 值和化学溶液初始pH 值.
不考虑化学反应的先后顺序,由反应前后H+离子浓度变化,得到某时刻与酸发生化学反应损失的可溶胶结物的摩尔数为[18]
式中,mi与ni为配平系数,cH+(t)为t时刻离子浓度值,c0H+为初始时刻离子浓度值,M和αi为化学反应系数.Vcs为化学溶液的体积.
结合式(6)、式(8)和式(10),可以得到考虑初始pH 值、时间t的化学损伤因子,其表达式如下
1.1.2 应力损伤变量
当岩石受到的应力大于其长期强度σs时,我们认为此时岩石发生应力损伤,根据Kachanov 蠕变损伤法则[19]得
式中,A,N是与材料有关的参数,Dm为应力损伤变量.
根据式(12)和边界条件t=tF和Dm=1 得到岩石在加速蠕变过程中损伤变量与蠕变时间的演化方程为
1.1.3 化学腐蚀和应力作用下的综合损伤变量
化学腐蚀造成的损伤在整个蠕变过程中都存在,而应力损伤发生在岩石受到的应力大于其长期强度σs时,结合式(5)、式(11)和式(13)可得岩石在酸蚀和应力作用下的综合损伤变量
1.2 真三轴蠕变模型建立
在岩石蠕变试验中,当初期施加的应力水平小于岩石的长期强度时,岩石试样在加载过程中首先会产生一个瞬时弹性应变,由于该阶段的加载时间在整个蠕变时间中占很小一部分,可认为该弹性应变是瞬间完成的,故该阶段的本构关系可用弹性体来描述,而考虑到岩石真三轴应力作用下的实际情况,本构方程为
继续加载,岩石进入衰减蠕变阶段,该阶段蠕变曲线具有明显的非线性特征,故采用经典元件模型难以准确描述其特征.本文通过引入损伤变量的时间函数关系来对传统Kelvin 模型中黏壶元件的黏性系数进行修正,即假定该黏性系数在岩石蠕变过程中与蠕变时间呈指数函数关系,从而构建非线性Kelvin 模型,其三维微分型本构方程满足
式中,σij为应力,G2,η2为非线性黏弹性阶段岩石的剪切模量和黏性系数,εnve为非线性黏弹性应变,为非线性黏弹性应变对时间的一阶导数,λ为待定常数,t为蠕变时间.
对上述微分方程分离变量,并结合初始条件t=0,,进行积分可得非线性Kelvin 体的蠕变方程为
随着应力的继续加载,岩石会发生黏弹性应变,本文使用Kelvin 模型来体现岩石流变过程中的这一阶段,本构方程为
当施加的应力水平超过岩石的长期强度时,岩石进入加速蠕变阶段,在三维应力的情况下,如果应力状态超过了黏塑性屈服面,则会开始产生黏塑性应变,采用Perzyna 的极限应力流动法则[20-22]来表示黏塑性应变的变化速率
式中,F为岩石的屈服函数,Q为塑性势函数,η4为与时间有关的黏滞系数.
基于式(13)、式(19)和式(20),可得到加速蠕变状态下的三维损伤本构方程[23]
将4 个阶段的本构模型联立,如图1 所示,根据模型串并联叠加原理可得岩石在真三轴应力状态下的黏弹塑性损伤蠕变模型的蠕变方程

图1 非线性黏弹塑性损伤蠕变力学模型Fig.1 Nonlinear viscoelastic plastic damage creep mechanical model
在真三轴的应力环境中,岩石在3 个方向上都受到应力,对于真三轴岩石蠕变试验有
岩石在三轴压缩过程中其破坏形式主要为沿着破坏面滑动的压剪破坏,由于岩石内部裂纹的生成和进一步发展和内部孔隙的扩大,岩石的黏滞系数会受到影响,故考虑损伤主要对剪切模量和黏滞系数造成的影响,忽略其对体积模量的影响[24],因此有
结合式(22)~ 式(24),可以得到岩石在真三轴应力状态下的黏弹塑性化学损伤蠕变模型的蠕变方程为
1.3 屈服面的确定
Mogi[25]对多种岩石进行了真三轴压缩试验,试验结果表明,中间主应力的存在对岩石破坏的强度有着重要的影响.基于冯-米赛斯准则,Mogi 提出一个考虑中间主应力的八面体强度应力准则,Al-Ajmi等[26]通过分析了多组岩石真三轴压缩试验数据,发现Mogi 提出的线性准则是适用于岩石真三轴压缩试验的,这个准则被称为Moji-Coulomb 准则,其表达式如下
式中,τoct为八面体应力,σm,2为有效正应力,C1与C2为试验常数,可由数据拟合得到.
当岩石所受的应力状态达到其应力屈服面时,岩石会发生明显的时间依赖性行为,基于三维应力下的Mogi-Coulomb 准则,得到岩石在三维空间中的损伤应力屈服面为
其中,I1为应力第一不变量,J2为第二偏应力不变量,θ为应力洛德角.
2 蠕变模型参数辨识与模型验证
2.1 参数辨识
因为考虑酸液腐蚀与真三轴应力同时作用的室内蠕变试验数据较为缺乏,因此利用酸性溶液腐蚀后的常规三轴岩石蠕变试验与真三轴应力作用下的岩石蠕变试验分别对本文的蠕变模型进行参数辨识与验证.
Wang 等[27]进行了砂岩在酸腐作用后的常规三轴蠕变试验,本文利用其试验中经过不同初始pH值溶液浸泡后的pH 值随时间变化的数据来验证式(5)的合理性,将溶液pH 值随时间变化的模拟值和实际测量值进行比较,如图2 所示,结果表明式(5)能很好的反应溶液pH 值随时间的变化趋势,验证了其合理性与正确性.
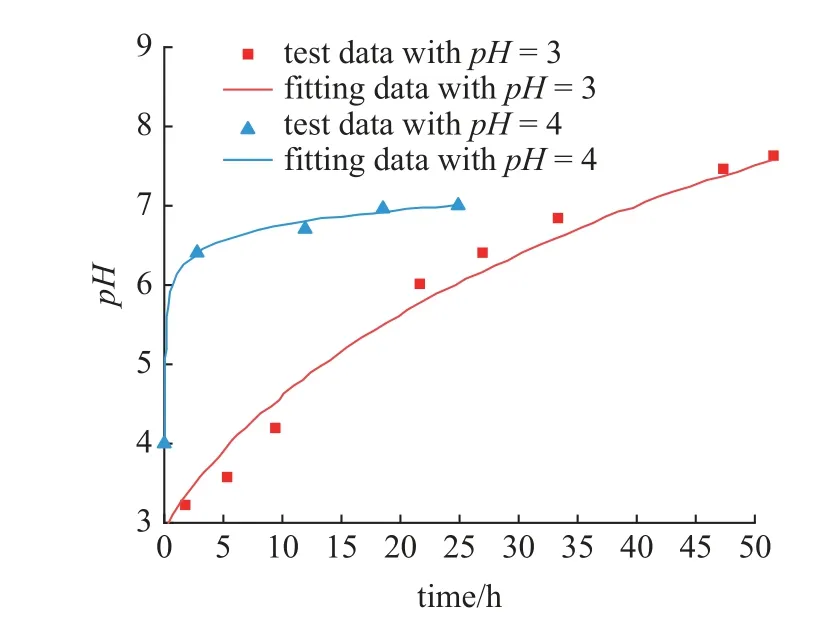
图2 溶液pH 值拟合结果与实测数据对比Fig.2 Comparison between the fitting results of solution pH value and the measured data
本文使用Wang 等[27]试验中的初始pH=3 的结果来验证本构模型的正确性与合理性,根据上图的拟合结果,式(9)中的p与x0分别为1.42 与1.15,化学损伤因子Dc根据式(11)与试验岩石的矿物组成可得为0.365.
Wang 等[7]进行的是岩石的常规三轴蠕变试验,是σ2=σ3的特殊情况,因此本文推导的蠕变本构模型可以得到很大的简化,根据岩石蠕变过程中的长期强度σs和应变速率作为本构方程各阶段的判断条件,模型还需确定的模型有G1,K1,λ,G2,η2,G3,η3,η4和N,岩石发生蠕变破坏的时间tF可根据试验数据确定,G1,K1根据岩石在同一围压下的常规三轴压缩试验得到的弹性模量E和泊松比v确定,即
岩石发生蠕变破坏的时间tF已根据岩石蠕变试验确定,其余模型参数基于最小二乘法原理反演确定: 运用Origin 软件自带的Levenberg-Marquardt 算法进行非线性回归分析,对岩石蠕变模型参数进行辨识,该算法改进了最小二乘法,通过引入阻尼因子d来避免迭代不收敛情况的发生[28].表1 为考虑化学损伤的岩石蠕变模型参数.图3 为考虑化学损伤的岩石蠕变试验曲线与理论曲线对比.
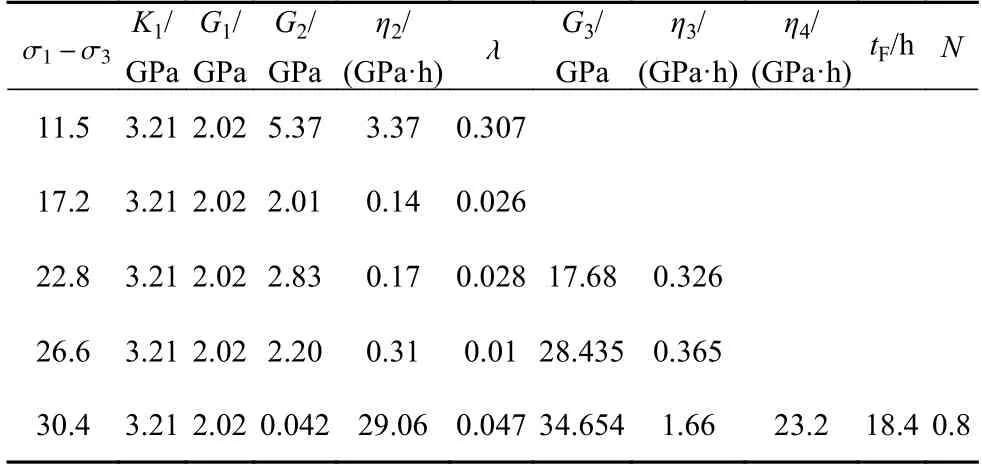
表1 考虑化学损伤的砂岩三轴蠕变模型参数(初始pH=3)Table 1 Sandstone triaxial creep model parameters considering chemical damage (initial pH=3)
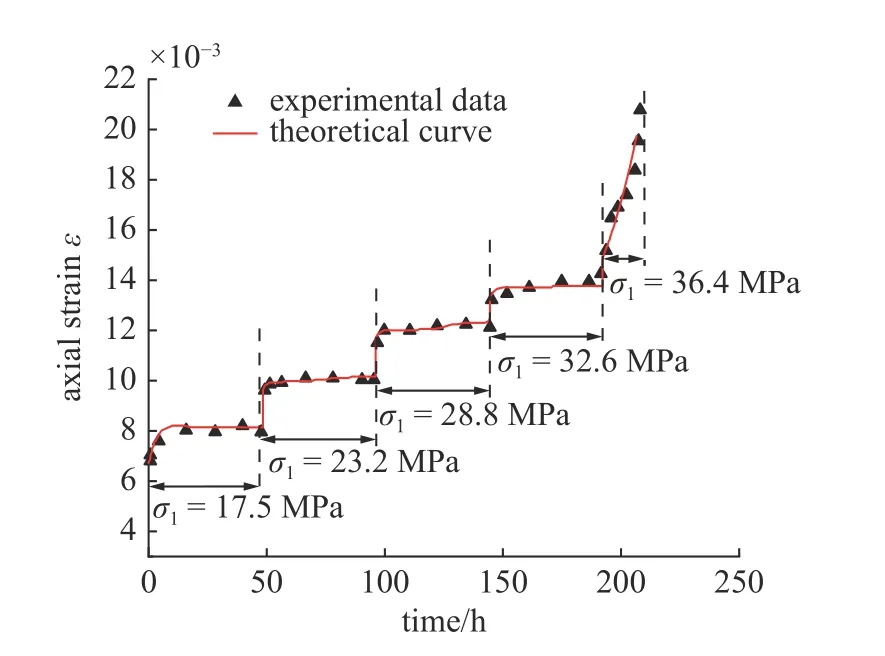
图3 考虑化学损伤的岩石蠕变试验曲线和本构曲线对比Fig.3 Comparison of rock creep experimental curve and constitutive curve considering chemical damage
Zhao 等[29-30]用锦屏大理岩进行了岩石在真三轴应力情况下的蠕变试验,得到了岩石在不同的中间主应力作用下蠕变的力学行为,可以看成化学损伤因子为0 的特殊情况,从而用以验证本文推导的本构模型在真三轴应力状态下的适用性,真三轴应力作用下的蠕变数据如下表2 所示,根据数据我们拟合得到八面体剪应力τoct与平均正应力σm,2的线性关系,从而得到式(26)中常数的大小,如图4 所示,C1=0.59701,C2=36.25189,代入到式(29)得到屈服面的表达式.
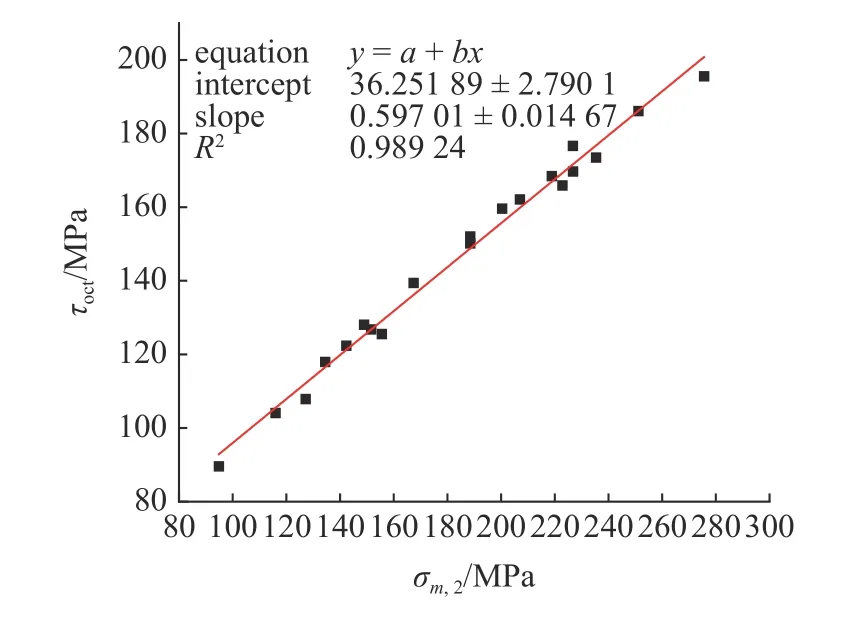
图4 八面体剪应力τoct 与平均正应力σm,2 的线性关系图Fig.4 Linear relationship between octahedral shear stress τoct and mean normal stress σm,2

表2 真三轴应力下的岩石损伤应力Table 2 Rock peak stress under true triaxial stress
真三轴应力作用下的本构模型参数的确定与上述过程一致,在三向应力情况下,本文选取了不同中间主应力下的岩石蠕变试验数据和不同最大主应力下的岩石蠕变数据分别进行验证,得到真三轴应力状态下的大理石蠕变参数如表3 所示.Zhao 等[29-30]进行的试验并不考虑岩石的化学损伤,因此对于本文推导的考虑化学损伤岩石蠕变方程来说,化学损伤因子Dc为0,结合上文已经得到的屈服面常数C1和C2与确定的本构模型参数,得到岩石在真三轴应力作用下的试验曲线与模型曲线的对比如图5所示.
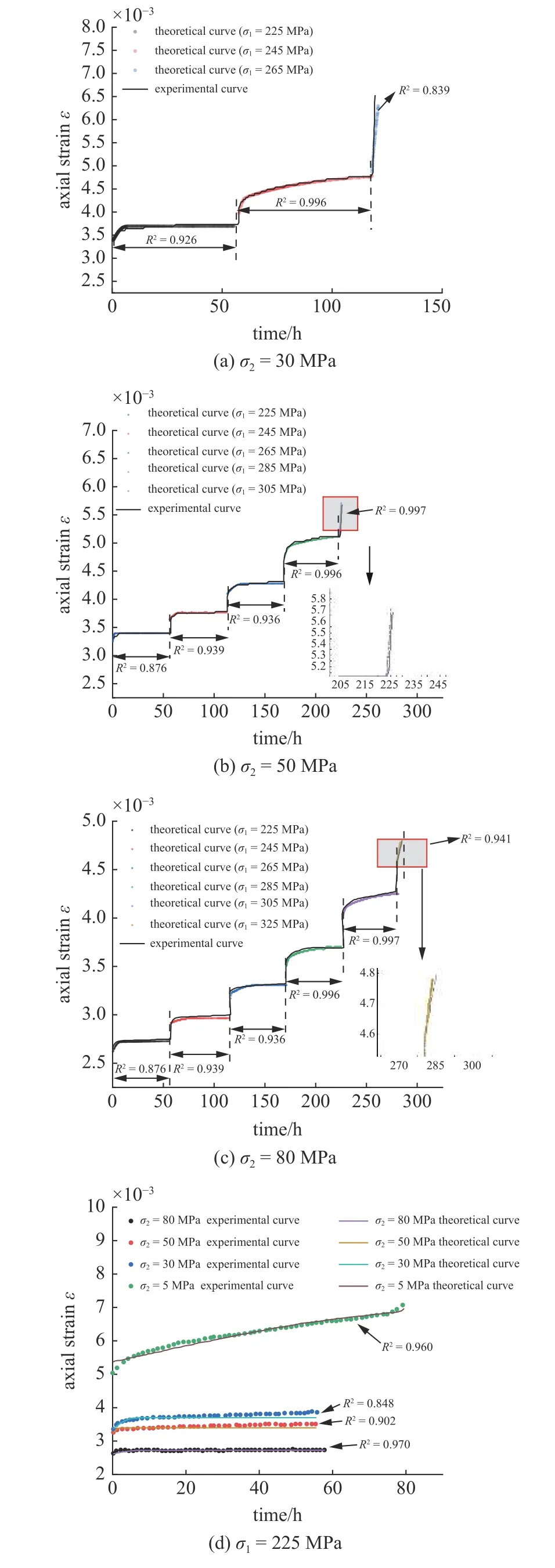
图5 真三轴应力作用下的大理岩实验曲线与模型曲线对比Fig.5 Comparison between experimental and model curves of marble under true triaxial stress
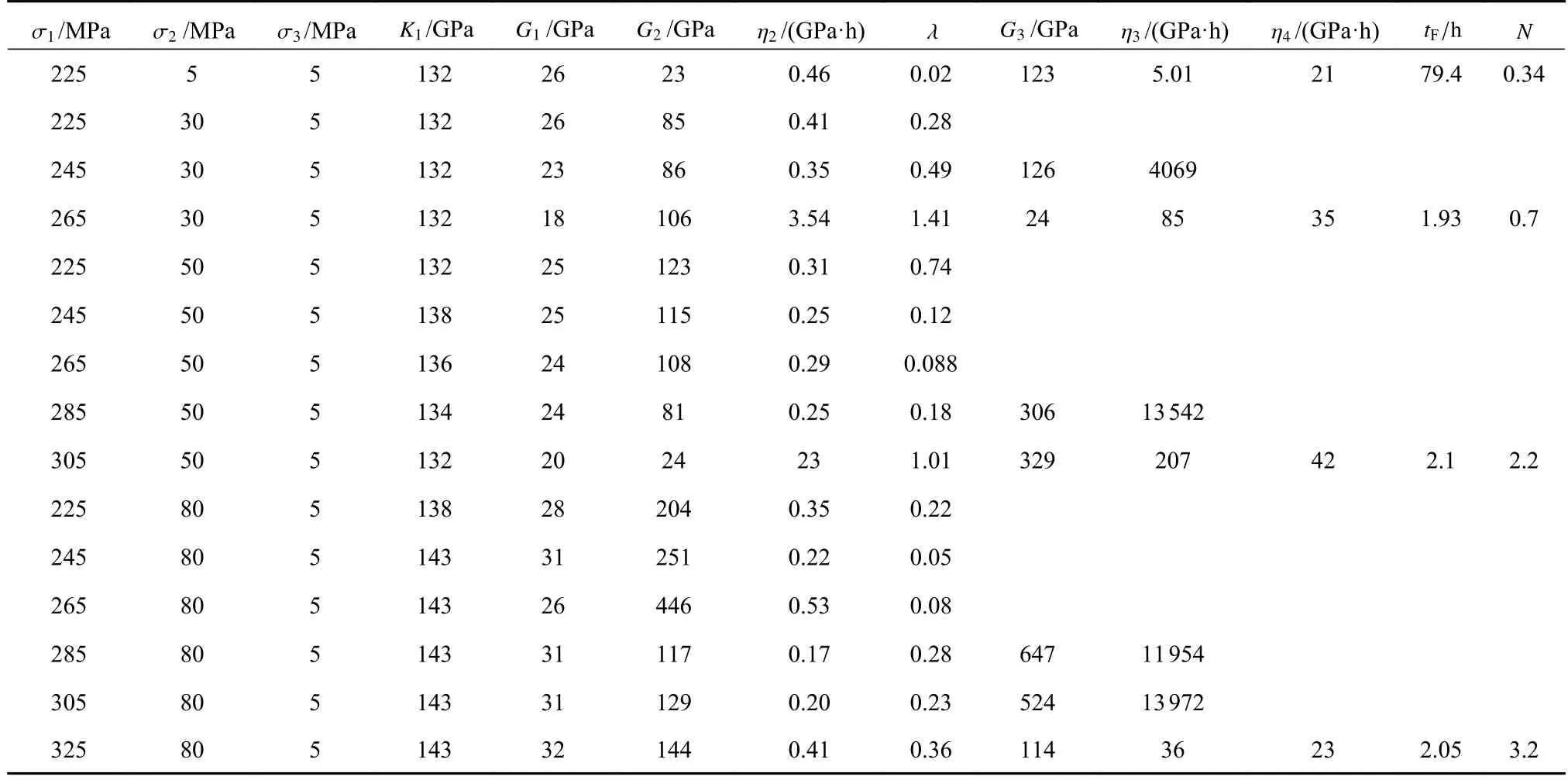
表3 真三轴应力作用下的大理岩蠕变模型参数Table 3 Parameters of the marble creep model under true triaxial stress
2.2 模型验证
对比图3 和图5 中的试验曲线和理论曲线,可以看到本文推导的岩石在水化学作用下的真三轴蠕变模型曲线与试验曲线较为符合,不仅能够反应化学损伤对岩石蠕变特性的影响,同时能反应岩石在真三轴应力作用下的蠕变行为,包括岩石蠕变的弹性阶段、衰减阶段、等速阶段和加速阶段.不同大小的中间主应力对岩石的蠕变行为会产生重要的影响,当第三主应力不变,中间主应力增大时,岩石蠕变破坏时间增大,破坏时的应变减小;通过对比在同一主应力和不同中间主应力作用下的岩石蠕变曲线,当中间主应力为5 MPa 时,岩石进入加速蠕变阶段,理论模型能很好的表现岩石进入破坏时的特征,而在其他水平的中主应力作用下,岩石蠕变则处于等速蠕变阶段,并没有发生破坏.同时我们可以看到当岩石蠕变处于加速阶段时,本构曲线与试验曲线的数据往往有一定的偏差,偏差平均在7%左右,这是因为在这个阶段岩石受到的应力已经大于其长期强度,岩石表面和内部产生的裂纹开始延展与贯通,导致这阶段的岩石的内部的应力不均匀分布.整体来看,本文建立的考虑化学腐蚀的真三轴蠕变模型能很好的反应岩石的蠕变各阶段行为,验证了模型建立的正确性和参数验证的合理性.
3 中间主应力对模型参数的影响
本文建立的岩石蠕变本构模型考虑了真三轴应力作用,因此,需要探讨不同中间主应力对模型参数的影响.通过得到不同中间主应力作用下岩石的蠕变模型参数,如下图6 所示,其中,剪切模量G2值的大小随着中间主应力的增加而上升,它作为一个弹性参数,随中间主应力的增大而逐渐增大.这表明,随着中间主应力的增加,岩石原有的裂纹、孔洞等微缺陷闭合,使岩石试样得到一定程度的硬化;黏滞系数η2的值随着中间主应力的增加呈现下降的趋势,黏滞系数η4的值随着中间主应力的增加呈现先增加而后减小的趋势.值得注意的是,当岩石进入加速蠕变阶段时,黏滞系数η3会大幅减小,从而使得岩石的蠕变速率增加,最终进入加速蠕变阶段,在本构模型曲线上体现为岩石应变的增加.在岩石蠕变未进入加速阶段而处于黏弹性应变时,黏滞系数η3的值很大,在宏观上表现为岩石蠕变速率的稳定,岩石所受到的外力还未达到岩石的长期强度.参数N随着中主应力的增加而呈现增大的趋势,同时可以观察到,当中主应力的水平较小时(σ2=5 MPa),岩石进入加速蠕变阶段所需的时间较大,当中主应力增加时,岩石蠕变破坏时间显著减小.
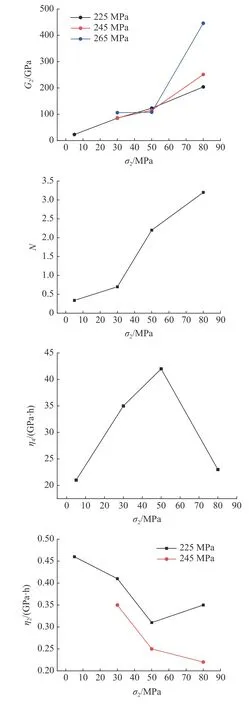
图6 不同中间主应力对模型参数的影响Fig.6 Effects of different intermediate principal stresses on model parameters
4 结论
(1)基于水岩作用的化学动力学理论,定义了考虑PH 值与时间的化学损伤因子,将弹性体,非线性Kelvin 体,线性Kelvin 体,黏弹塑性体((Mogi-Coulomb)进行串联,并同时考虑真三轴应力作用下的实际情况,建立了考虑岩石酸腐与真三轴应力耦合作用下的损伤蠕变本构模型.
(2)采用考虑化学腐蚀的岩石蠕变实验结果和真三轴应力作用下的岩石蠕变结果分别对模型进行了验证,得到了化学损伤因子和考虑真三轴应力作用的岩石屈服面,结果表明,建立的本构模型能很好的反应岩石在酸腐作用和真三轴应力状态下的蠕变特性,验证了其合理性与参数确定的正确性.
(3)该蠕变模型不仅能够准确地描述岩石的瞬时弹性应变阶段、等速蠕变阶段的蠕变曲线特征,而且能够较好地描述岩石衰减蠕变阶段和加速蠕变阶段蠕变曲线的非线性特征.
(4)分析了不同中间主应力对岩石参数的影响,剪切模量G2值的大小随着中间主应力的增加而上升;黏滞系数η2的值随着中间主应力的增加呈现下降的趋势,黏滞系数η4的值随着中间主应力的增加呈现先增加而后减小的趋势;当岩石进入加速蠕变阶段时,黏滞系数η3会大幅减小;参数N随着中主应力的增加而呈现增大的趋势,当中主应力增加时,岩石蠕变破坏时间显著减小.

