平面幂律塑性I型裂纹尖端应力场全解1)
王志强 蔡力勋 黄茂波
(西南交通大学力学与航空航天学院,应用力学与结构安全四川省重点实验室,成都 610031)
引言
在航空航天、船舶、核电和化工等工程中,裂纹构件的裂纹尖端应力场与断裂强度是结构安全评价的重要基础.
Cherepanov[1]和Rice[2]分别在1967 年和1968年针对含I 型裂纹无限体各自独立提出与裂纹尖端环向积分路径无关的J积分.随后,Hutchinson[3]、Rice 等[4](HRR) 针对幂律硬化材料,基于J积分和塑性解析求解在理论上给出描述裂尖应力场的HRR 奇异解,该解关于角度分布的解析描述一直未得到解决.1983 年,Shih[5]考虑幂律塑性应力−应变关系,通过有限元分析计算了HRR 解中的积分常数IN和无量纲角度函数,相关结果均由数值表格形式给出.1991 年,Betegon 等[6]利用边界层方法研究小范围屈服条件下不同T应力(T11,作用于裂纹面且垂直于裂纹前沿的应力分量)对弹塑性应力场的影响,提出J-T11方法,该方法以T11作为表征裂尖约束程度的弹性参量用于描述I 型裂纹有限尺寸试样的弹塑性裂尖场.后继研究[7-9]表明,具有弹性属性的T应力不适用于大范围或全范围屈服条件.1991 年,对于中心裂纹板和单边裂纹弯曲两个有限几何尺寸试样,O’Dowd等[10-11]为反映有限尺寸对裂尖场的几何约束效应,考虑在HRR 场基础上进行约束补偿,提出J-Q方法,该方法对不同材料和试样的不同几何尺寸,完全依赖有限元分析,所获得Q值有不同结果,无普适性Q方程,应用不便.1986 年Li 等[12]提出含高次展开项的幂律塑性渐进解作为HRR 场约束补偿项的新思路,1991 年Sharma 等[7]及1993 年Yang 等[13]采用一次高阶渐近项作为HRR 场补偿项提出了裂尖场描述模型,该模型通过复杂数值分析仅对特定材料和几何工况给出渐进解参数,相较HRR 场描述精度上有了提升,不过,对于不同材料和不同几何工况需给出不同渐进解参数,普适性仍然不足.Yang等[8,14]基于裂纹尖端应力场的3 项渐近展开式,给出了第二和第三展开项的系数之间的近似关系,提出了J-A2理论.Nikishkov 等[9,15]采用类似方法,提出J-A理论,本质上和J-A2理论一样[16-17].随后,Ding 等[18-19]进行广泛的有限元分析,获得经验方程,预测约束参数A,Q,A2等参数.上述应力渐进解均无关于角度的描述函数.事实上,任何复杂函数关系都可以由不同函数,如高阶级数函数、特殊函数等函数同时表征,描述形式并非唯一.Ji 等[20-21]通过数值分析提出特殊的指数函数来表征特定材料具有奇异性的弹塑性应力场,虽然该修正的奇异性指数并没有适用于不同材料和几何条件的统一表达式,但这是针对塑性裂尖奇异场研究提出的一个重要概念和新方法.
此外,也有学者在研究断裂韧性时尝试将裂尖塑性区与裂尖约束联系起来.Anderson 等[22]提出A-D 法,即用裂尖前最大正应力σ1与屈服应力σy的比值来表征约束,比值越大,约束越大.Mostafavi等[23-26]对A-D 法进行了改进,用试样或结构断裂时的裂尖塑性区面积Ac与标准高约束平面应变断裂韧性试样断裂时的裂尖塑性区面积Assy(参考塑性区面积)的比值 φ来表征约束水平来表征约束水平,用φ可以将任何约束(不同的面内和面外约束)水平下的断裂韧性JIC试验数据关联起来,建立一致性的断裂韧性与约束的关联线.
本文考虑幂律塑性本构关系,基于能量密度等效原理[27-29]和量纲分析提出具有中值能量密度的代表性体积单元 (representative volume element,RVE)的等效应力(σM)解析方程,以能量密度等效体积单元的应力因子为应力特征量,提出平面幂律塑性I 型裂纹尖端应力场半解析模型.针对有限平面应变和平面应力紧凑拉伸(compact tension,CT)试样和单边裂纹弯曲(single edge bend,SEB)试样,给出应力场半解析模型参数的确定方法,并进行数值分析的模型验证.
1 理论模型
1.1 等效应力解析方程
假设延性材料均匀连续、各向同性,对于受单向加载的任意构元(见图1),Chen 等[27-29]基于复杂应力与单轴应力下 RVE 应变能密度等效(图1中任意A点RVE)及应变能密度中值等效(图1 中值M点RVE),提出弹塑性应变能U控制方程为
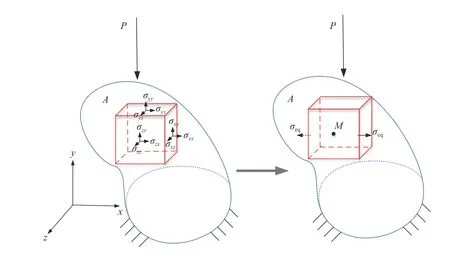
图1 能量密度等效示意图Fig.1 Schematic diagram of energy density equivalence
式中,Veff为有效变形域体积,εeq−M为RVE 等效应变.
幂律塑性条件下,设材料应力应变关系符合幂律
式中,εp−eq为等效塑性应变,σeq为等效应力,K为材料的应变硬化系数,N为应力硬化指数.进一步假定Veff,εp−eq与加载线位移hp之间符合幂律关系
式中,特征体积V*为A*h*,A*为特征面积;h*为特征位移;k1和k2分别为有效体积系数和有效体积指数,k3和k4分别为等效塑性应变系数和等效塑性应变指数.
由式(1)、式(2)和式(3)得到幂律塑性应变能Up控制方程
根据文献[27-28],受单向加载构元的载荷−位移关系表示为
式中,P为载荷,P*为特征载荷,ζp和mp分别为幂律塑性条件下的无量纲载荷−位移关系系数和指数,m为体积折减系数.
能量密度中值点RVE 的等效应力σM与载荷P及加载线位移hp与构元特征尺寸分别构成相似判据π1,π2,设为
假定π1和π2之间关系符合幂律
式中,k5和k6分别为等效应力系数和等效应力指数.由式(6)和式(7)可得
联立式(4)和式(8),整理可得
在准静态加载和幂律塑性条件下,根据功-能原理,载荷对构元试样所做的功等于构元试样的变形能(U),进而由上式可得
将式(5)的载荷P代入式(10)中整理可得
上式等号左右项积分整理可得
考虑到等号右端项为常数,则等号左端项的无量纲变量hp/h*的指数项必为0,则1−(k2+k4+k6)=0,此时右端项必为1,进而可得
结合幂律应变式(4)、关于P与hp的无量纲式(8)及k5,k6表达式(13),可得σM解析方程,定义该应力为应力因子
1.2 平面I 型裂纹尖端应力场半解析模型
对于I 型裂纹构元,有效变形体积在加载过程中保持不变,则式(4)中k2为0;由文献[30]可知幂律塑性条件下中值点RVE 等效应变与试样加载线位移之间呈线性关系,即,式(4)中k4为1.则k5=(k1k3)−1,k6=0.进一步由式(4)、式(5) RVE 等效应力的解析方程可简化为
对于有限尺寸试样,裂纹尖端应力场不再符合HRR 解.考虑HRR 解的奇异性,对裂尖应力,以应力因子σM作为特征应力,则基于特征应力的无量纲裂尖应力表为
式中,当sub 为eq 时,σeq是等效应力,当sub 为ij时,σij是应力张量(ij=11 时为rr,ij=22 时为θθ,ij=12 时为rθ),σM是特征应力,L是特征长度(通常取为1 mm),f和λ为关于N与θ的函数,m为试样尺寸a/W的综合指数.
考虑到HRR 场奇异性指数为1/(N+1),对分子、分母各叠加一个关于θ增量β’sub,即(1+β’sub)/(N+1+β’sub),可进一步假设fsub=βsub/(N+βsub),βsub=1+β’sub,βsub为与三角函数相关的特殊函数,即
式中,dsubp(p=0,1,2,3)为待定参数.
有限元计算表明幂律塑性条件下裂尖等效应力等值线在平面应变和平面应力下分别具有蝶翅轮廓和扇贝轮廓的特征,为描述这两类特殊的等应力轮廓线,设应力分布系数λsub为三角特殊函数
式中,psubk(k=0,1,2)与qsubm(m=0,1,2,3)为待定参数,psubk(k=0,1,2)与N相关,csubk(k=0,1,2),bsubk(k=0,1,2) 为psubk的待定参数.
修正综合指数msub与N相关,假设
式中,msub0和msub1为待定参数.
联立式(16)~ 式(19)可得平面幂律塑性I 型裂纹尖端应力场半解析模型
若式(16) 中 λeq·(L/r)feq取为不同程度常数C,则由式(17)、式(18)有
选择合适的级数项数和相应参数,可在数学上使上述函数能恰当描述蝶翅轮廓式或扇贝轮廓式等应力线,进而由式(20)可推导出平面I 型裂纹有限尺寸试样等效应力等值线表达式
2 有限元分析
2.1 分析条件
本文采用有限元分析(finite element analysis,FEA)软件ANSYS19.0 对CT 试样和SEB 试样进行研究,本文所针对CT 试样和SEB 试样的建模参数标定及模型验证都针对有限尺寸试样.几何构型如图2 所示,a为裂纹长度,b为裂纹剩余韧带长度.
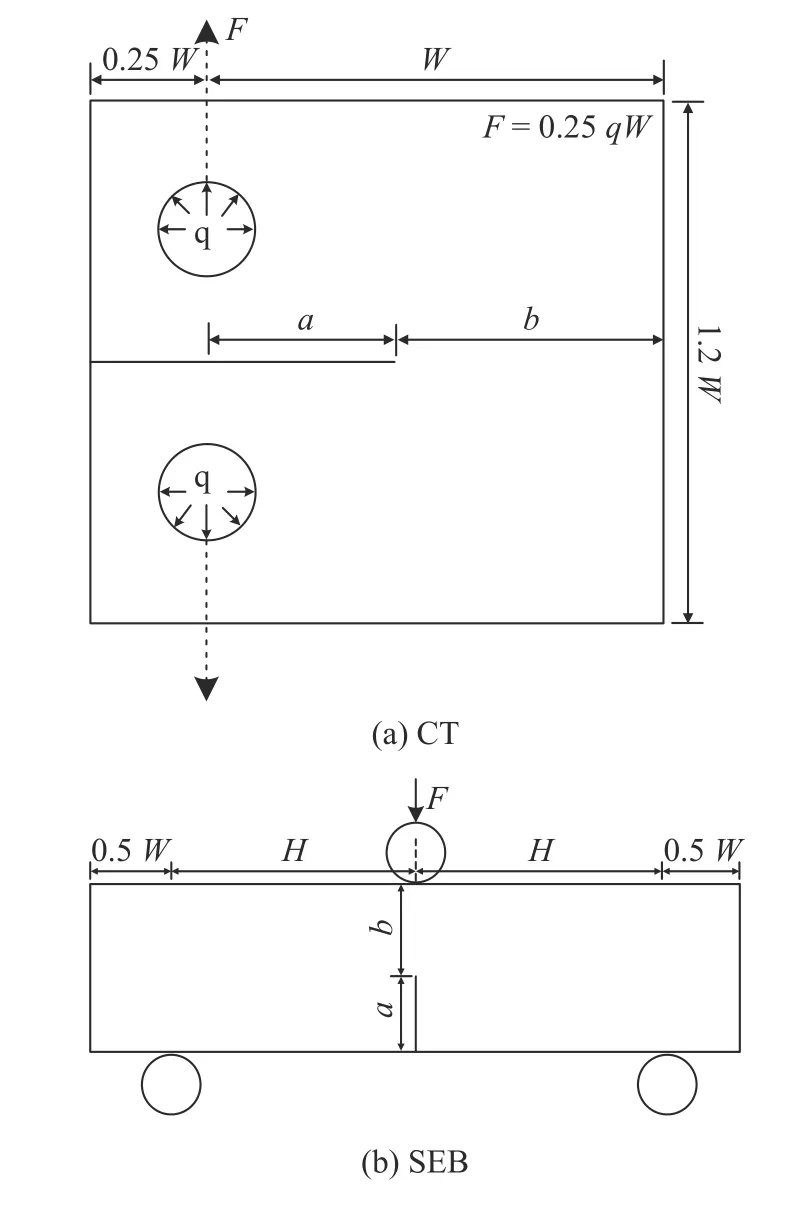
图2 试样示意图Fig.2 Schematic diagram of specimens
由于对称性,图3 给出了试样的有限元分析的1/2模型,CT 试样的宽度W为50 mm,SEB 试样的宽度W为20 mm,其跨度H和宽度W之比H/W为2.裂纹尖端采用1/4 节点奇异单元(KSCON),其余部分均采用4 节点单元(Plane182),裂纹剩余韧带部分施加对称约束边界条件.CT 试样采用销钉孔上半圆内边缘施加法向等效均布压载荷(合力F即为试样的载荷,F=0.25qW),考虑销钉加载时加载孔X方向固定,对加载孔上方接触点施加X向约束;SEB 试样采用压头位移加载,压头(或加载辊)均采用Target169单元,构元试样表面均采用contact 172单元.
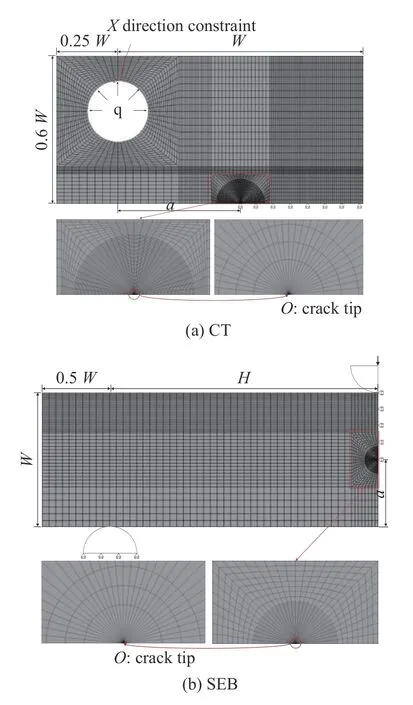
图3 FEA 模型图Fig.3 FEA model of specimens
2.2 FEA 模型验证
为在网格模型设计中选用合适网格密度,需考察裂尖附近不同网格密度对 FEA 结果的影响,针对有限平面应变(plane strain)、平面应力(plane stress)条件的CT 试样,有限元分析预设材料本构关系为幂律,即式(2),预设K:1000 MPa,N:10,a/W: 0.5 完成幂律塑性分析,考察裂尖附近不同网格密度下的应力分布.定义图3 中所示距裂尖5 mm扇形范围内单元尺寸为 1 倍网格密度(扇形单元径向尺寸S为0.08 mm),2 倍、4 倍、8 倍网格密度定义为对裂尖扇形区网格加密为1 倍网格密度的相应倍数(扇形单元径向尺寸S相应为0.04 mm,0.02 mm,0.01 mm).图4 和图5 中图例的标记符号NE和NN分别表示不同密度下扇形网格区沿径向单元总数和节点数.图4 和图5 分别给出了有限平面应变和平面应力条件下不同网格密度CT 试样 的FEA 获取的载荷位移曲线和裂尖等效应力分布,结果表明,采用 1 倍网格密度时已经满足计算要求.
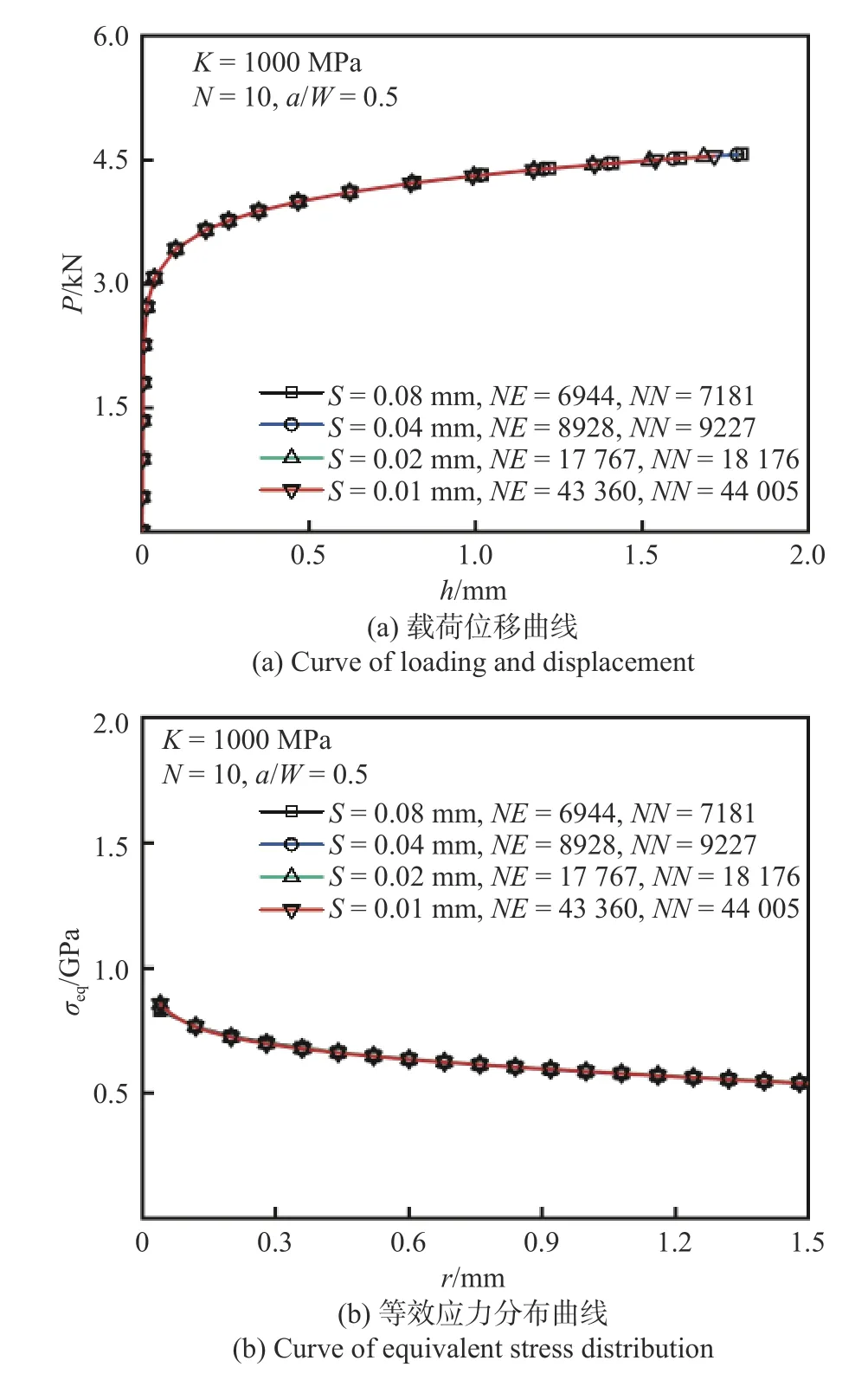
图4 平面应变条件下裂尖附近网格密度对FEA 结果的影响Fig.4 Effects of element meshing size around the crack tip on the FEA results under plane strain conditions
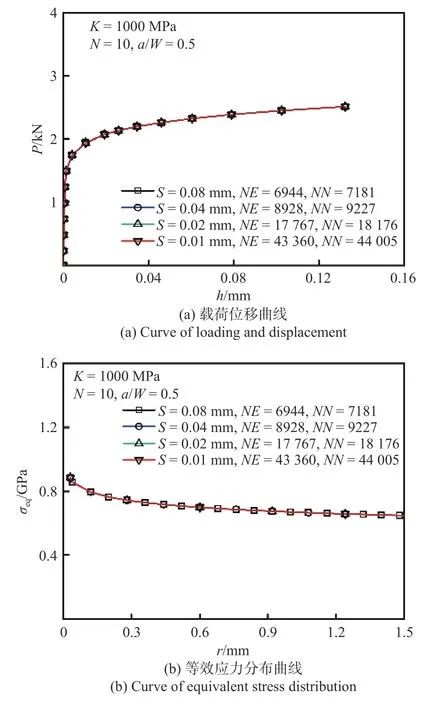
图5 平面应力条件下裂尖附近网格密度对FEA 结果的影响Fig.5 Effects of element meshing size around the crack tip on the FEA results under plane stress conditions
2.3 模型参数的确定
为了更加了解式(20)的特征,以下部分以平面应变条件下CT 试样的应力分布为例,给出了参数确定方法.
2.3.1 综合指数m和修正综合指数msub
选取无量纲裂纹长度a/W为0.45~ 0.75(间隔0.05),应变硬化系数K为1000 MPa,应力硬化指数N分别为12,10,6 和4,在幂律塑性条件下进行计算.文献[30]给出了CT 和SEB 试样在平面应变条件下的体积折减系数m与参数k1~k4,进而通过式(15)得到k5,用同样方法可标定出平面应力条件下体积折减系数m与等效应力系数k5,方程(15)参数如表1 所示.

表1 方程(15)模型参数Table 1 Parameters of Eq.(15)
进一步以应力因子σM为特征量,对不同无量纲裂纹长度a/W与应力硬化指数N下无量纲应力σsub/σM~r/L幂律拟合得到系数λsub,在给定应力硬化指数N时,将系数λsub与无量纲裂纹长度(1−a/W)幂律拟合得到msub,接着在不同N条件拟合出式(19)的待定参数msub0和msub1.图6 为修正综合指数参数标定过程,表2 给出了CT 和SEB 试样分别在平面应变和平面应力条件下的待定参数msub0和msub1.在以下研究中,以σM作为特征应力,获得裂尖的无量纲应力分布分析参数βsub和λsub.
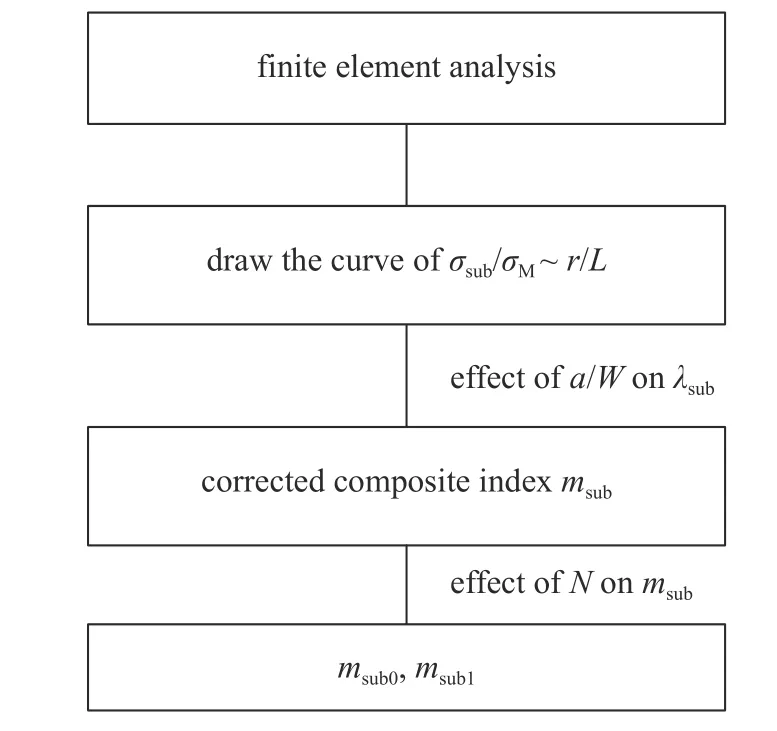
图6 参数标定Fig.6 Calibration parameter
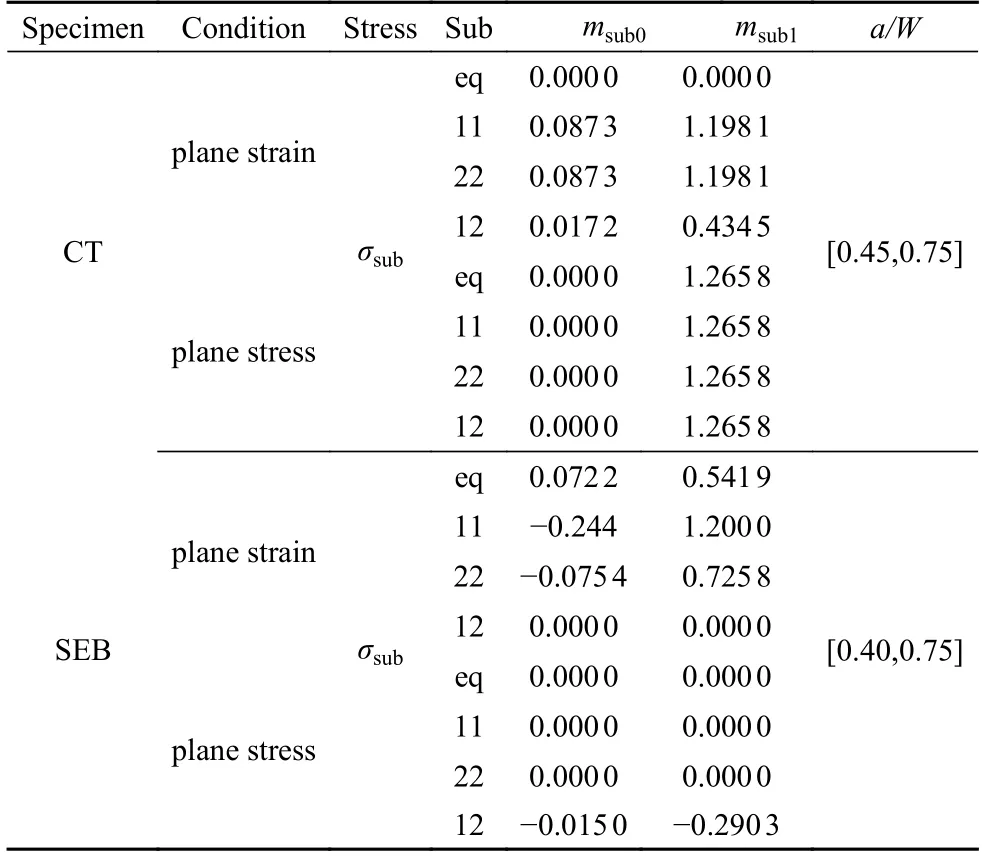
表2 方程(19)参数Table 2 Parameters of Eq.(19)
2.3.2 奇异性指数fsub及其参数βsub
参考常用材料,选取无量纲裂纹长度a/W为0.6,应变硬化系数K为1000 MPa,应力硬化指数N分别为12,10,6 和4,在幂律塑性条件下进行计算.在距离裂纹尖端0.06b范围内的应力分布可用关于L/r的幂函数进行描述,其奇异性分布指数fsub可由回归确定;考虑到应力的奇异性主要体现在裂纹尖端附近的右扇形区,故主要关注应力在θ=0 到θ=π/2 的等效应力分布,在平面应变条件下得到各个角度的fsub和对应的βsub.参数βsub与θ关系如图7 所示,由(17)可得三角函数关系如下
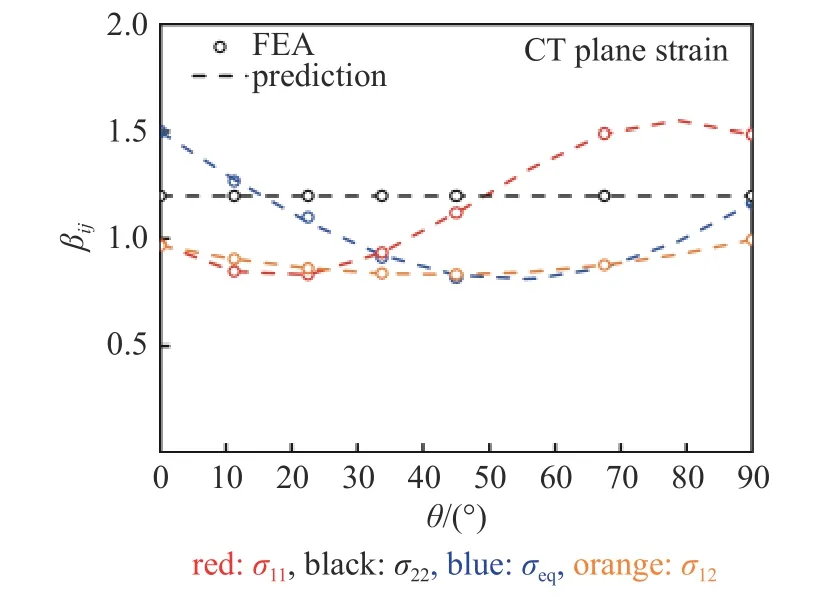
图7 角度θ 对β 影响Fig.7 Effect of θ on β
式中,dsubp(p=0,1,2,3)为待定参数.
类似可得到平面条件下βsub与θ的关系,表3给出了CT 和SEB 试样分别在平面应变和平面应力条件下的参数dsubp(p=1,2,3,4)
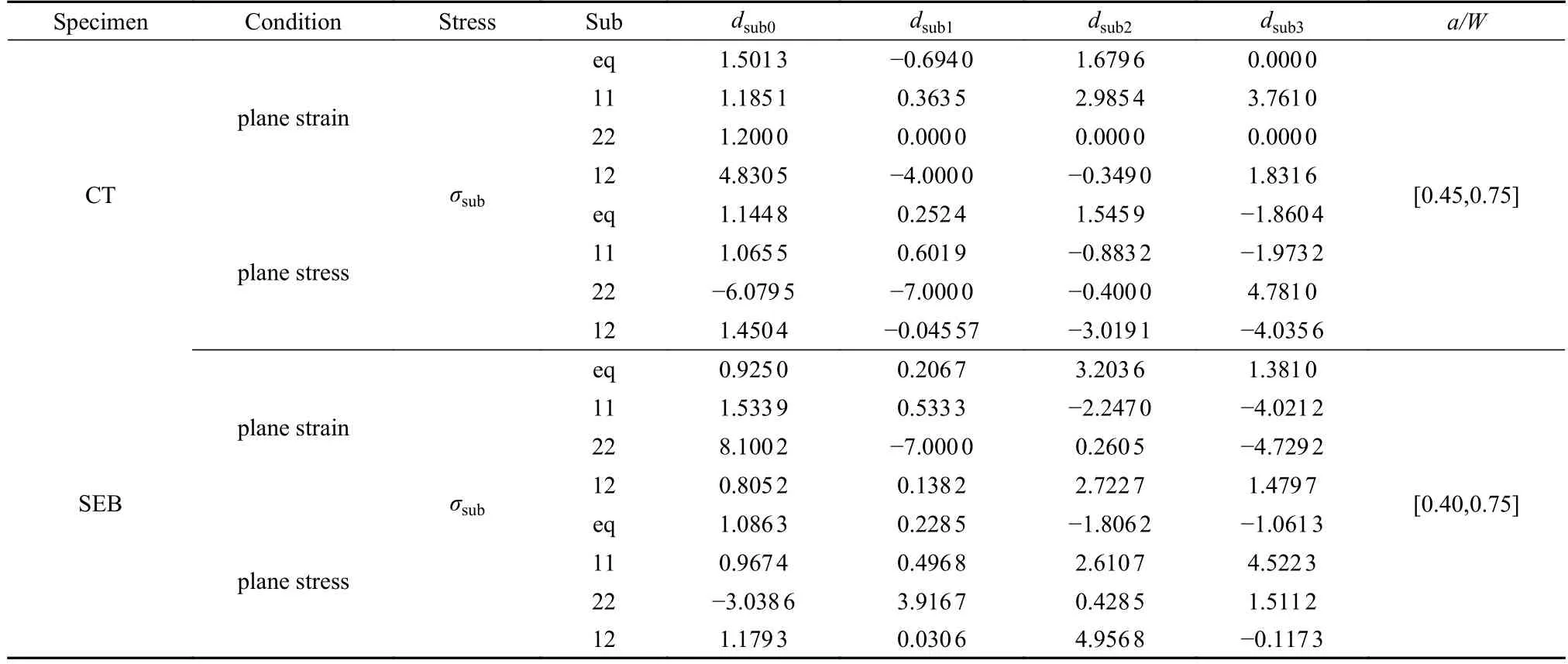
表3 方程(23)模型参数Table 3 Parameters of Eq.(23)
2.3.3 无量纲应力分布系数λsub
为考虑各类因素对无量纲应力分布系数λsub的影响,以平面应变条件下试样裂纹面(θ=0)的应力分布为例,将应力硬化指数N固定为10,以σM作为特征应力,获得裂尖的无量纲应力分布,以此分析λsub.图8 给出了载荷P和应力硬化系数K对λsub的影响,表明无量纲应力分布系数λsub与载荷P和应力硬化系数K无关.

图8 载荷P 和应力硬化系数K 对λsub 的影响Fig.8 Effects of loading P and strain hardening coefficient K on the λsub
将无量纲裂纹长度a/W和应变硬化系数K分别固定为0.6 和1000 MPa,以σM作为特征应力,获得无量纲应力分布系数λsub如图9 所示,在不同硬化指数下,λsub随θ呈规律性变化;psub0与psub1均可以近似表示为与硬化指数N幂律相关的函数,如图10所示.类比三角特殊函数表征线弹性裂尖应力场[31],式(18)整理可得不同应力的λsub如下

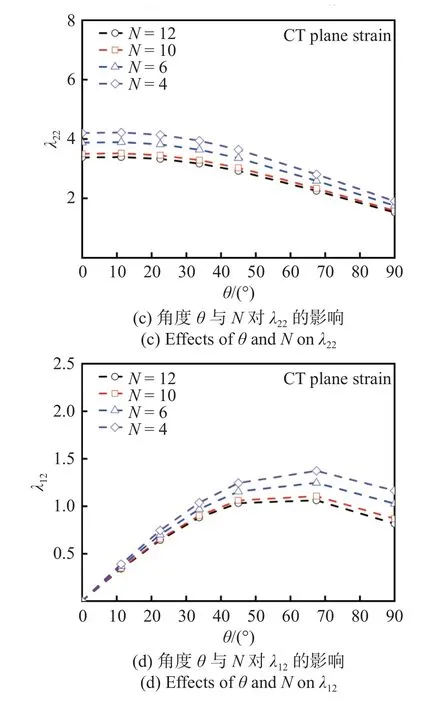
图9 角度θ 与N 对λsub 的影响Fig.9 Effects of θ and N on λsub
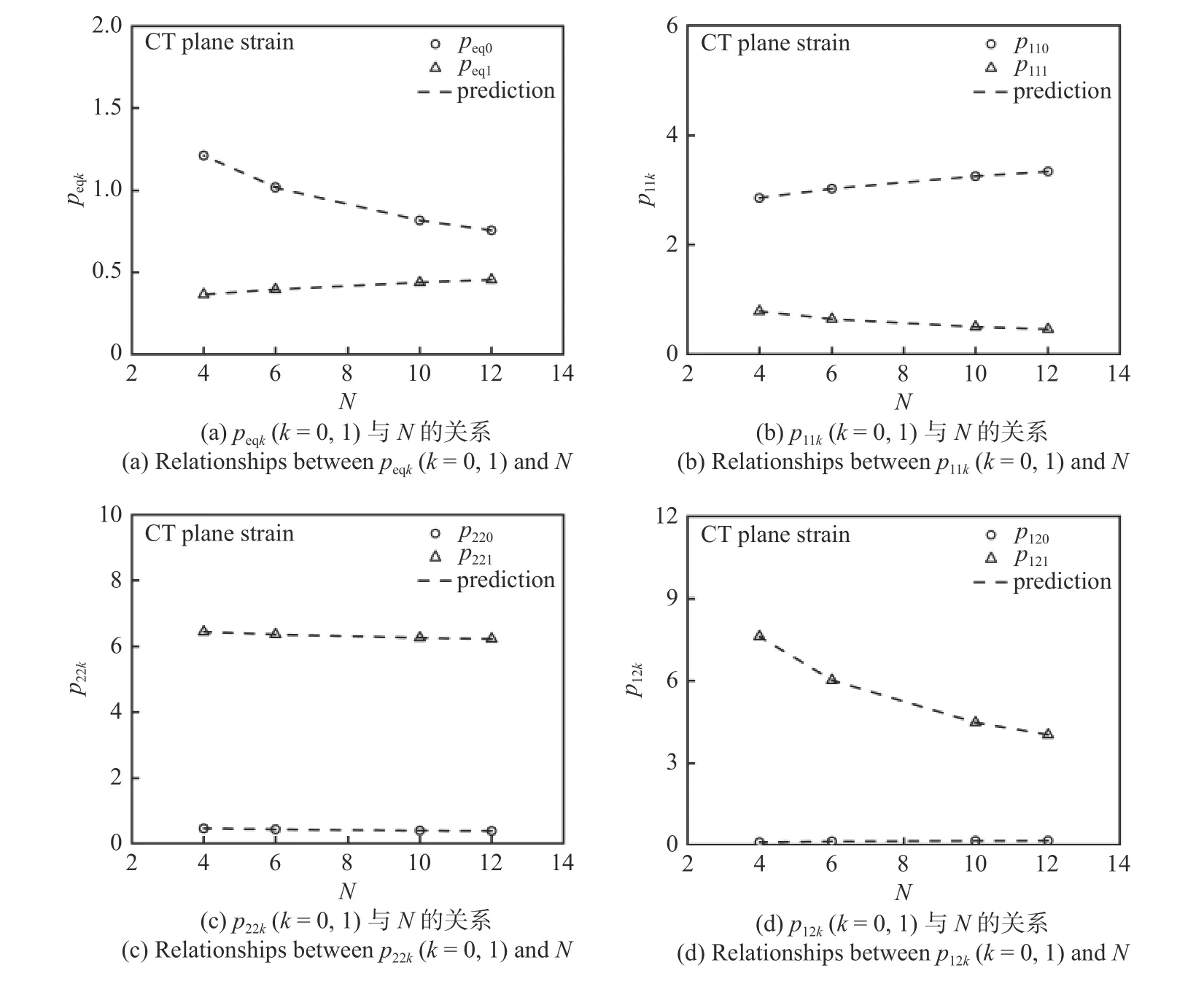
图10 psubk(k=0,1)与N 的关系Fig.10 Relationships between psubk(k=0,1) and N
式中,psubk(k=0,1)与qsubm(m=0,1,2,3)为待定参数,psubk(k=0,1)与N相关,csubk(k=0,1),bsubk(k=0,1)为psubk(k=0,1)的待定参数.
综上,平面幂律塑性I 型裂纹尖端应力场半解析模型可显式表达为
式中,参数csubk,bsubk(k=0,1) 与参数qsubm(k=0,1,2,3)列于表4.
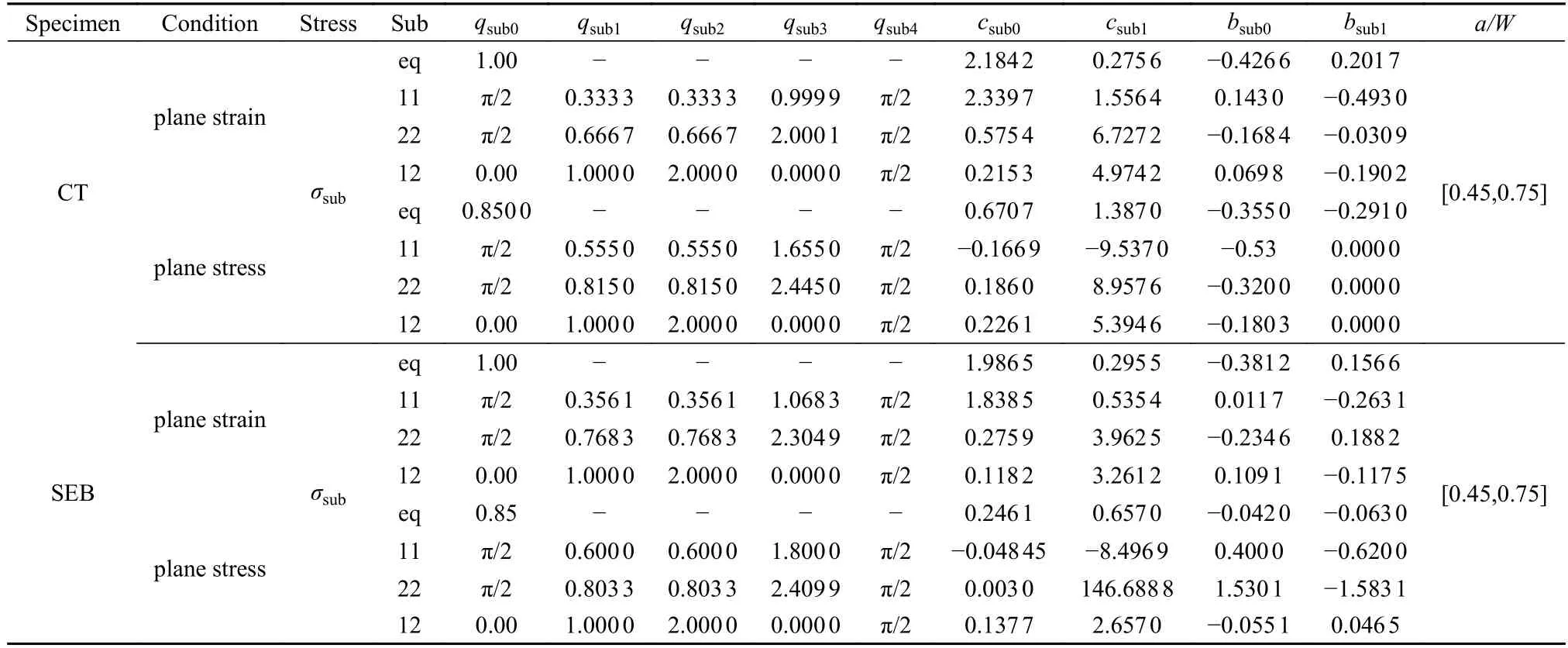
表4 模型参数Table 4 Parameters of model
3 模型验证
3.1 应力分布的验证
图8 表明应力分布系数λsub与应力硬化系数K无关,而本文标定参数选用硬化指数N=4,6,10,12,故本文模型材料参数使用范围为N=4~ 12,表1~表4 给出了相应的公式参数及其适用范围,根据式(25)可预测CT 试样和SEB 试样的裂尖应力分布.图11~ 图14 分别给出了CT 试样和SEB 试样在平面应变、平面应力条件下的不同裂纹长度和不同硬化指数下,FEA 和本文公式预测的径向应力分布对比;图15~ 图18 分别给出了CT 试样和SEB 试样在平面应变、平面应力条件下的不同裂纹长度和不同硬化指数下,裂纹尖端径向距离不同情况下的FEA 和本文公式预测的环向应力分布对比.结果表明本文模型预测的结果与FEA 结果均吻合良好.
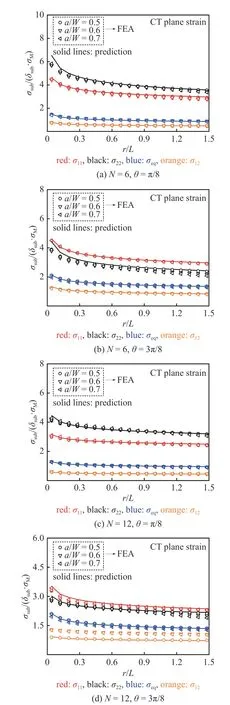
图11 CT 试样平面应变条件下裂尖无量纲应力径向分布对比Fig.11 Comparison with FEA and predicted results by Eq.(25) for normalized stress radial distributions near the crack tip of CT specimens under plane strain conditions
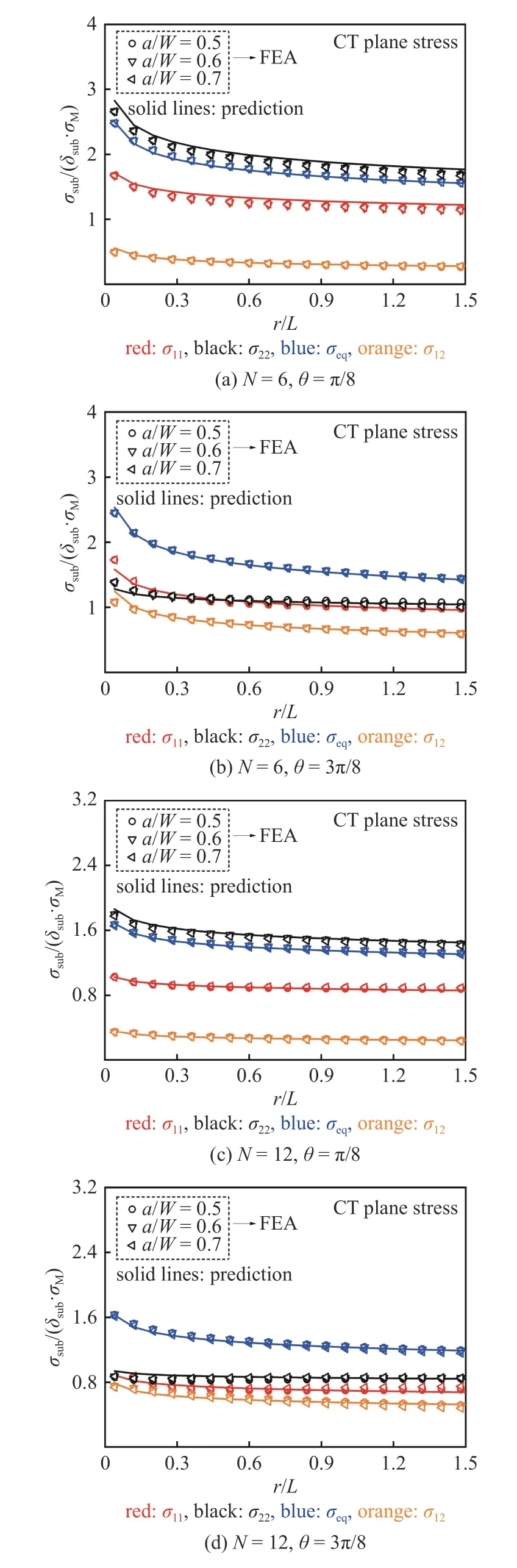
图12 CT 试样平面应力条件下裂尖无量纲应力径向分布对比Fig.12 Comparison with FEA and predicted results by Eq.(25) for normalized stress radial distributions near the crack tip of CT specimens under plane stress conditions
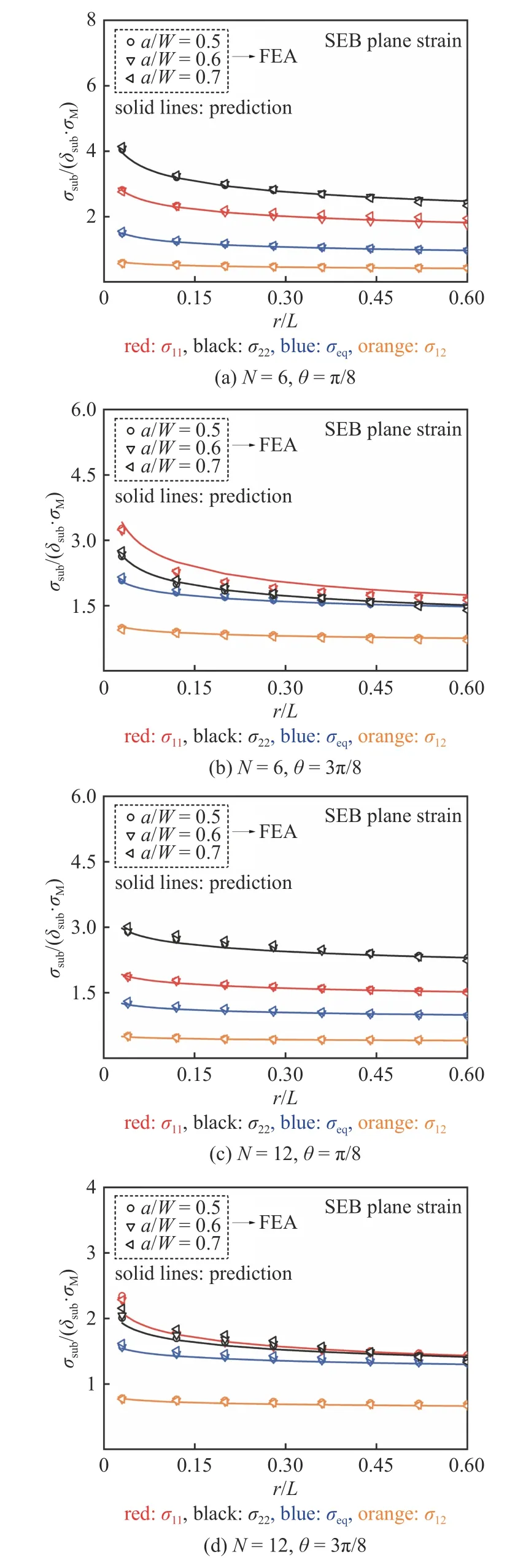
图13 SEB 试样平面应变条件下裂尖无量纲应力径向分布对比Fig.13 Comparison with FEA and predicted results by Eq.(25) for normalized stress radial distributions near the crack tip of SEB specimens under plane strain conditions

图14 SEB 试样平面应力条件下裂尖无量纲应力径向分布对比Fig.14 Comparison with FEA and predicted results by Eq.(25) for normalized stress radial distributions near the crack tip of SEB specimens under plane stress conditions
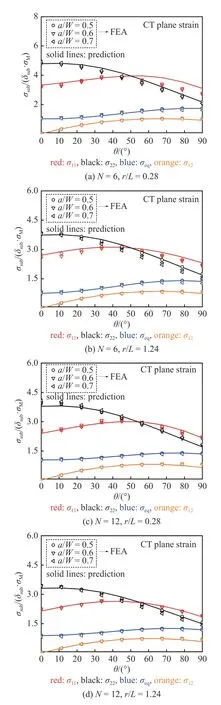
图15 CT 试样平面应变条件下裂尖无量纲应力环向分布对比Fig.15 Comparison with FEA and predicted results by Eq.(25) for normalized stress angular distributions near the crack tip of CT specimens under plane strain conditions

图16 CT 试样平面应力条件下裂尖无量纲应力环向分布对比Fig.16 Comparison with FEA and predicted results by Eq.(25) for normalized stress angular distributions near the crack tip of CT specimens under plane stress conditions
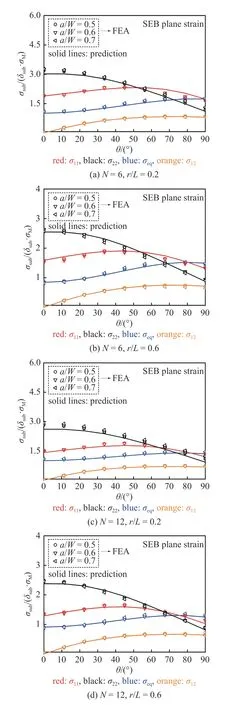
图17 SEB 试样平面应变条件下裂尖无量纲应力环向分布对比Fig.17 Comparison with FEA and predicted results by Eq.(25) for normalized stress angular distributions near the crack tip of SEB specimens under plane strain conditions

图18 SEB 试样平面应力条件下裂尖无量纲应力环向分布对比Fig.18 Comparison with FEA and predicted results by Eq.(25) for normalized stress angular distributions near the crack tip of SEB specimens under plane stress conditions
3.2 等效应力等值线验证
根据式(25)可推导出平面I 型裂纹有限尺寸试样等效应力等值线表达式
考虑极限载荷PL表达式为[32]
图19、图20 和图21、图22 分别给出了CT试样和SEB 试样加载到极限载荷PL时,不同裂纹长度和硬化指数下,有限元分析得到的等效应力等值线与方程(26)预测的等效应力等值线对比,当等效应力σeq达到屈服应力σ0时,等效应力等值线表示塑性区边界.结果显示,预测的结果与有限元分析结果吻合良好.

图19 CT 试样平面应变条件下等效应力σeq 等效应力等值线对比Fig.19 Comparison with FEA results predicted by Eq.(26) for contour lines of the equivalent stress σeq near the crack tip of CT specimen under plane strain conditions

图20 SEB 试样平面应变条件下等效应力σeq 等效应力等值线对比Fig.20 Comparison with FEA results predicted by Eq.(26) for contour lines of the equivalent stress σeq near the crack tip of SEB specimen under plane strain conditions
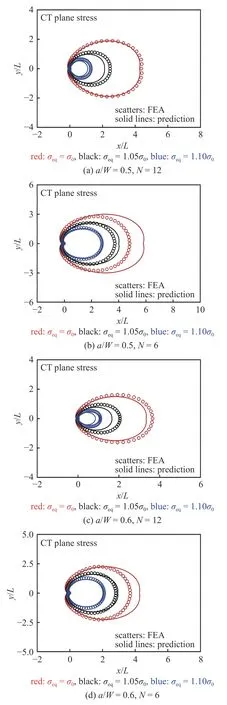
图21 CT 试样平面应力条件下等效应力σeq 等效应力等值线对比Fig.21 Comparison with FEA results predicted by Eq.(26) for contour lines of the equivalent stress σeq near the crack tip of CT specimen under plane stress conditions
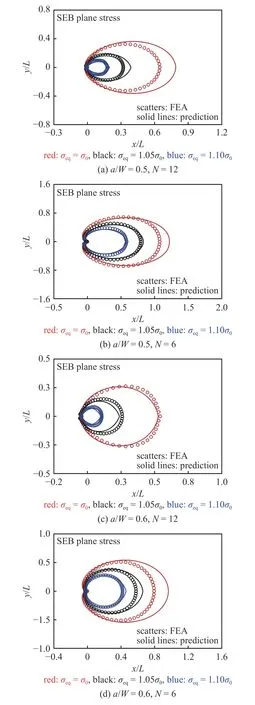
图22 SEB 试样平面应力条件下等效应力σeq 等效应力等值线对比Fig.22 Comparison with FEA results predicted by Eq.(26) for contour lines of the equivalent stress σeq near the crack tip of SEB specimen under plane stress conditions
4 结论
(1) 基于能量密度等效和量纲分析方法,推导了受单向加载构元试样中值能量密度RVE 的等效应力解析方程,并定义其为σM应力因子;
(2) 以应力因子σM作为特征应力,采用可用于裂尖等效应力等值线表征的蝶翅轮廓式(平面应变)和扇贝轮廓式(平面应力)的三角特殊函数,提出描述平面应变和平面应力幂律塑性I 型裂纹尖端应力场的半解析模型;
(3) 针对平面应变和平面应力CT 和SEB 试样,本文模型预测的应力场与有限元分析结果均吻合良好.

