基于递阶优化的城市区域路网交通控制
吉柯,唐进君,曾捷,刘鑫源
(中南大学 交通运输工程学院,湖南 长沙 410075)
城市居民的出行在工作日均具有早晚高峰现象。对于高等级道路来说,在高峰期往往伴随着需要多次停车、道路拥挤、等待时间长的情况。与此同时,车流常常具有显著的潮汐性,同一条道路在不同时刻2个方向上具有很明显的流量差。对于城市道路而言,虽然高峰期存在较为明显的拥堵现象,但并不是所有的道路都拥堵。主干路、次干路等道路可能存在较高的延误,但仍存在着利用率不高的次干路和支路。对此,如何有效利用饱和度偏低的路段分流高饱和度路段的车流,实现路网压力均衡,成为了目前研究的热点问题。对信号配时进行优化是交叉口优化的基本手段之一,近年来也出现了许多与新技术相结合的优化方法。赵纯等[1]采用基于深度Q-Learning的方法来优化信号配时,采用深度神经网络进行训练和输出,结果表明改进后的深度强化学习可以动态的控制信号配时,相较于传统静态配时,该方法的控制效果更佳。卢凯等[2]则是从绿波的角度,基于车速和信号协同制定了一套信号控制方案。牟亮等[3]基于快速非支配排序遗传算法(NSGA-Ⅱ)提出了一种改进的区域信号控制方案。虽然学者们的研究切入点各不相同,但都是在向着动态、区域性等目标进行研究。信号配时的优化目标已不再是单点或单线的问题,而是转向对于某个区域进行协调控制。近年来,对于城市路网的协调控制研究层出不穷。梁超等[4]设计了一种区域交通流量协调控制器,对路网密度进行平衡,试验表明在这种控制下,路网的平均密度有所下降、车辆速度有所提升、车辆延误有所下降。郭亚娟[5]基于社团发现提出了拥堵区域预警,在此基础之上结合宏观基本图提出了路网动态边界控制策略。申慧[6]提出了一种单向全通行的控制方法,用于解决车流冲突及车辆排队问题;在路段溢流问题上,提出了相关三转向车流的同步控制方法加以控制;在路网划分问题上,提出了基于重叠划分的交叉口分组方法。双层模型作为一种常见的模型,上下2层优化目标相对独立,但求解结果能够协调优化目标,得出全局最优,在交通优化领域的应用也十分广泛。王秋平等[7]结合历史街区的交通问题,基于双层规划模型提出了基于微循环的交通优化方案。高雪溢[8]也采用了相同的方法,选用速度最大、延误最小等指标作为上层模型的决策目标,并基于层次分析法构建了评价方法。研究结果都表明,双层规划模型对于交通优化有良好的效果。但是,目前双层模型在指标的选取方面仍偏向于常见指标,如速度、延误等,本文以道路反压力值作为优化指标,相对于常见指标而言,可以直观的表现出道路压力情况;同时,由于反压力控制方法具有寻找反压力值最大的特点,因此利用反压力值可以很好的进行单点信号控制优化。在双层模型的基础之上,可在道路网络设计、道路交通管控措施和信号配时实时控制等多个方面进行递阶优化控制。徐云雯[9]提出以递阶优化对大规模路网进行控制优化,采用状态转移概率模型进行信号控制,建立了混合反压力控制的大规模路网递阶优化控制模型。陈斌[10]则是建立了交通状态评价函数,以大系统递阶控制思想构建了交通控制和交通流诱导的协同模型。二位学者的研究都使用VISSIM仿真软件进行了模拟验证,所提出的方案得到了较好的验证,但仿真道路环境均为假设环境,道路状态较为理想化,缺乏在实际路网当中的应用验证。本文以长沙市道路网络作为研究对象,以实际道路环境在VISSIM软件搭建仿真路网,利用实测车牌识别数据校正仿真模型,采用递阶优化思想构建双层模型。其中,上层模型中以路网反压力指标最优为优化目标,下层模型采用改进韦伯斯特算法作为控制方案;最后在仿真中验证优化模型的可行性与优势。
1 基础数据及仿真路网
1.1 路网概况
本文选用的研究区域是长沙市城市道路区域路网,如图1所示。该区域北至五一大道、南至城南西路、西至蔡锷南路、东至曙光路。该区域内包含主干路、次干路等多种道路等级,路幅宽度也覆盖了双向2车道至双向10车道。结合湖南省长沙市的车牌识别系统(License Plate Recognition,LPR)所覆盖的交叉口,将研究路网抽象为具有23个交叉口的路网,如图2所示。图2所示共计23个交叉口,其中,10号交叉口南北方向和东西方向在空间上不交叉,此交叉口不存在信号配时,因此在后期研究中并未针对该交叉口进行优化。

图1 研究区域Fig. 1 Study area

图2 抽象路网Fig. 2 Abstract network
1.2 数据概况
本文的研究重点在于针对路网的拥堵情况进行调节,因此选取了工作日的早高峰时段作为研究的时间范围。研究范围内,早高峰交通拥堵较为严重,直行车辆的2次排队情况非常普遍,如交叉口1-9-13-16-20沿线,虽然道路多为双向8车道和双向10车道,但仍存在较大的交通压力。结合LPR系统所采集到的数据进行分析,本文选取了2019年7月1日至7月5日连续5个工作日的车流量进行分析。选取时间段为早7时至9时,该时间段内每日流量分布具有相似趋势,为便于流量输入,采用取平均值的方式进行处理,将数据作为研究路网的车流量数据,表1为部分交叉口的基础信息。

表1 部分交叉口基本信息Table 1 Basic information of some intersections
除车流量数据外,本文同步收集了研究范围内22个交叉口的信号配时参数。由于各交叉口面积、车道数等原因,信号周期从100~190 s不等,信号周期时长跨度较大,如图3所示。从现状来看,交叉口信号周期时长大致分为两类,部分支路及次干路相交的交叉口信号周期在120 s以下,而信号周期时长较大的交叉口时间多分布于140~190 s之间。

图3 研究范围内各交叉口信号周期时长Fig. 3 Signal cycle time of intersection in the study area
1.3 仿真路网
基于已获取的基础数据,本文采用VISSIM软件对研究区域的路网进行仿真模拟。在进行路网搭建前对实际道路条件进行了调查,详细记录了各类交通信息,如车道数量、进口道长度、有无特殊车道及特殊交通管控等。在此基础之上绘制得出如图4所示的仿真路网。

图4 仿真路网Fig. 4 Simulation of road network
在该路网上输入经过处理的LPR系统采集数据,输入端仅包括路网的边界交叉口,即交叉口1,2,3,4,6,8,9,12,13,15,16,19,20,21,22和23。并在交叉口进口道处设置数据采集器,以一小时作为评价周期,测量通过每一个进口车道的车辆数,汇总得出每个交叉口的通过车辆数。将其与LPR系统采集得出的数据进行对比,得出如图5所示的结果。针对误差率大于0.1的1,18和19号交叉口,以进口道方向计算了误差率,如表2所示。

图5 仿真结果与真实数据的差异Fig. 5 Differences between simulation results and real data

表2 部分交叉口误差率Table 2 Differences between simulation results and real data of some intersections
由图5可以看出,22个路口中评价数据与真实数据差异最大的交叉口为18号交叉口,差异率为14.08%。86.3%的交叉口误差率控制在10%以下,说明本文搭建的仿真路网与实际环境具有较高的相似性。
2 递阶优化控制模型
2.1 反压力指标
反压力控制算法最初应用于数据传输方面[11],反压力控制由于其寻找最大压力值的特点可被应用于单个交叉口的信号控制[12-14]。对于任意路段l,在任意时刻k可根据交通量、路段长度等参数得出反压力值wl(k)[15],见式(1)。
其中:xl,m(k)表示在k时刻由路段l到路段m的车辆数;rm,h(k)表示从k时刻到k+1时刻内由路段m到路段h的转弯率,rm,h(k)∈(0,1);om表示路段m的下游合集,如图6所示。

图6 反压力参数示意图Fig. 6 Schematic diagram of back pressure parameters
本文所选用的数据为车道级别,因此,针对每一车道的交通流可获取一个反压力值,在此基础之上,应进一步计算交叉口的反压力指标。对于交叉口u而言,整个交叉口的反压力指标值pu(k)计算如公式(2)。
其中:Uu代表交叉口u的相位集合;uu代表交叉口u的相位;sl,m(k)表示从k时刻到k+1时刻内由路段l到路段m的信号值;cl,m(k)表示从k时刻到k+1时刻内由路段l到路段m的交通流的饱和流速。
在计算得出单一交叉口的反压力值后,需要计算得出整个路网的反压力指标值γ(k),以该值作为优化依据。
其中,δl是路段l的权系数,用于平衡路网中不同路段的延迟时间。
同时,在计算得出交叉口的反压力值后,可以通过信号控制矩阵su(k)确定当前交叉口在下一个优化周期内的控制策略。
2.2 递阶优化模型
考虑以反压力指标作为路网的实时判别参数,在此基础之上,引入双层优化模型,上层以路段反压力指标作为输入参数,结合优化目标和限制条件确定信号矩阵及最优控制方案。下层以采用改进韦伯斯特算法作为控制算法,确定交叉口的信号控制方案。在确定的优化周期下,对路网的信号控制进行优化。
2.2.1 上层模型
对于上层模型,优化目标即为计算得出的整体路网反压力指标最优,即式(4)。约束条件方面,一方面对于交叉口u,在k时刻的相位un有开和关两种形式,分别为1和0,在k时刻时,整个路口的相位un的累加和为1,保证只有单一相位处于开放状态,即式(5)。另一方面对于道路p来说,压力指标可以通过分周期采集的数据计算得出,但对于交通量既有输入又有输出的路段来说,需要同时考虑输入和输出两种情况,只考虑压力指标数值有可能会产生超过道路性能的情况,导致求解没有意义,因此需要对道路承载力进行约束,即式(6)。
目标函数及限制条件如下式:
其中:xl,m(k)表示k时刻从路段l到路段m的车辆数;zl,m(k)表示从k时刻到k+1时刻内路径p的交通需求量;hl,m(k)表示从k时刻到k+1时刻内路段l到路段m的车辆数。
2.2.2 下层模型
对于下层模型,主要集中在路网范围内单个信号交叉口的配时方案决策控制。根据现有的交通流采集数据和信号配时数据得出,部分路口如14和18号交叉口饱和度偏高,不太适用于常规的韦伯斯特配时方法,因此考虑参考金勇等[16]的研究,在韦伯斯特有效绿灯时间的概念中,加入交叉口通行能力最大和车均延误最低为目标函数,单一相位满足临界条件为约束的模型。以此作为改进韦伯斯特算法,进行下层决策控制。
其中:Q为交叉口通行能力;Sij为i相位中的j车道组的饱和流率;gi为i相位的有效绿灯时间;C为交叉口周期;d为交叉口每辆车的平均延误;qij为i相位中的j车道组的流量;dij为相位中的j车道组的平均延误;yi为i相位的流量比;Y为交叉口总流量比;L为每周期总损失时间;Cmin为最小周期时间;Cmax为最大周期时间。
在进行交叉口控制优化时,为便于形成稳定的区域性信号协调信号控制,考虑采用新的配时周期。因研究区域内22个信号控制交叉口的复杂程度不同,考虑以90 s和180 s 2个周期作为新的配时周期。对于原方案中高饱和度、进口车道数多的交叉口采用180 s大周期,而原方案中交通压力较低的交叉口则采用90 s小周期。
3 仿真结果分析
3.1 仿真结果
为对比提出优化模型的有效性,本文设置了3种运行方案,方案1采用当前固定配时方案;方案2采用递阶优化控制,但下层模型仅采用常规韦伯斯特控制算法;方案3采用递阶优化控制,下层模型采用改进韦伯斯特控制算法。
对于路网的通行效率,采用在网车辆数和到达车辆数两个指标进行对比,如图7和图8所示。其中,在网车辆数表示进入路网的车辆中在当前时刻仍处于路网上行驶的车辆数;到达车辆数表示进入路网的车辆中在当前时刻已行驶至路网边界的车辆数。
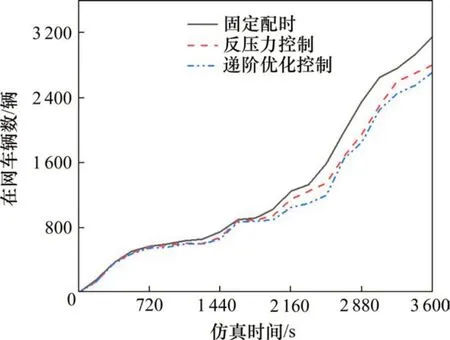
图7 在网车辆数Fig. 7 Number of vehicles running on the road network

图8 到达车辆数Fig. 8 Number of vehicles arriving at the boundary
从图7和图8可以看出,对于在网车辆数,方案2和方案3相较于方案1均有所降低,说明优化方案与原始方案相较,道路饱和度有所下降,对于拥堵路段具有一定的疏导作用;到达车辆数在1 440 s后方案2和方案3相较于方案1也有了显著提高,说明优化后车辆的通行效率提高,更多的车辆能够在一定的仿真时间内到达研究边界,方案3在路网通行效率方面提升程度略高于方案2。在对单个交叉口数据进行对比后发现,高饱和度交叉口在使用递阶优化控制后交叉口通行效率有所提高。
从车辆角度考虑,选取车均延误和车辆速度2个指标进行对比,如图9和图10所示。

图9 车均延误Fig. 9 Average vehicle delay

图10 车均速度Fig. 10 Average vehicle speed
图9中,方案2与方案3的延误增长与方案1相比更加平缓,延误相对较低。因此对于方案2和方案3来说,延误变化趋势差别不大。图10中,方案2与方案3在网车辆的行驶速度高于方案1,其中,方案3车辆行驶速度更高。因此,该结果说明本文采用的双层递阶控制方法具有更好的控制效果。
3.2 分析讨论
从仿真结果来看,使用递阶优化模型进行路网控制后,整体路网在各个评价指标上都有所提升。但针对高饱和度提出的改进韦伯斯特算法的应用效果,在对比中并不明显。
因此考虑将饱和度等于0.6作为划分点,将22个信号交叉口划分为A和B 2类,交叉口饱和度大于0.6定义为A类,包括交叉口1,9,11,12,14,16,18和20。其余交叉口定义为B类,再对4类指标进行对比,得出如下所示结果。

图11 不同饱和度交叉口仿真结果对比Fig. 11 Simulation results of intersections with different saturation
A类交叉口作为饱和度较高的交叉口,同时车道数较多,B类则车道数较少,双向4车道居多。在对比中可以看出,A类交叉口无论是在网车辆数还是通过车辆数,都与总体形式相接近;而B类交叉口的数据变化幅度不大。A类交叉口的在网车辆数在后期远高于B类交叉口,说明A类交叉口的拥堵情况更加严重。在速度和延误方面,两类交叉口的数据变化趋势与整体相接近。B类交叉口虽然通过车辆数不及A类交叉口,但在延误方面相对低,在速度方面相对高,也符合高峰时期的实际情况。
在递阶优化控制中,考虑到部分交叉口可能出现高饱和度的情况,改进了传统韦伯斯特算法。针对改进算法对不同饱和度交叉口的影响做出了如图12所示的结果。

图12 改进算法对不同饱和度交叉口的影响Fig. 12 Influence of improved algorithm on intersections with different saturation
从图中来看,由于针对高饱和度交叉口对配时算法进行了改进,A类交叉口在网车辆数下降的幅度要高于B类交叉口,同时,A类交叉口的车均延误下降幅度也高于B类交叉口,说明递阶优化控制对高饱和度交叉口的通行效率具有更明显的改善。同时在到达车辆数方面,以递阶优化控制的A和B 2类交叉口的到达车辆数都有一定的提升幅度;而在递阶优化控制下,A类交叉口的速度虽然在数值上不如B类交叉口,但与未改进算法的控制效果相比,递阶优化控制对高饱和度交叉口的车辆速度具有更好的改善作用。因此,该结果表明本文提出的递阶控制方法对不同饱和度情况下的交叉口均有较好的控制效果。
本文采用的双层递阶控制方法针对当前数据具有一定的优化效果,但同时需要一定的设备成本,用以提供数据基础。取得的优化效果和实施成本与实际路网的交通饱和度相关,当交通饱和度高于本研究同时仍处于可控状态下,则可以取得相对更加明显的优化效果。
4 结论
1) 在网车辆数减少表明控制方案对于拥堵路段具有疏导作用,到达车辆数增加表明路网通行效率得到提高。
2) 对于在路网中运行的车辆来说,车辆速度的提高和车均延误的下降均表明车辆行驶更加顺畅,车辆通行效率得到提高,具有更好的驾驶感受。
3) 在下层控制中,考虑到传统韦伯斯特方法对高饱和度状态适用度不高,因此采用了改进韦伯斯特算法。该方法有效地提高了高饱和度路口的通行效率。

