高速铁路CRTS Ⅲ 型轨道板隔离层关键构件-弹性垫板试验

蒋丽忠 ，刘丽丽，周旺保 ，彭东航，冯玉林

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 高速铁路建造技术国家工程研究中心，湖南 长沙 410075；3. 华东交通大学 土木建筑学院，江西 南昌 330013)

近年来，高速铁路渐渐成为人们生活中不可或缺的出行工具，高速铁路必须满足高速列车行车安全性和乘坐舒适性的要求[1]。轨道结构作为高速铁路系统重要的组成部分之一，其对高速铁路列车的安全平稳运行具有很大影响[2-3]。2008年我国开展了板式无砟轨道结构体系的自主创新和优化设计研究，研发了具有我国自主知识产权的新型板式无砟轨道结构形式—CRTS Ⅲ型板式无砟轨道。这种新型板式无砟轨道结构体系先后在武汉城市圈城际铁路、盘营客运专线、沈丹客运专线、郑徐高速铁路、京沈高速铁路等工程中得到了推广应用[4-5]。列车荷载反复作用下CRTS Ⅲ 型板式无砟轨道系统各关键构件的受力性能，对高速列车的行车安全性和乘坐舒适性具有明显影响。LI等[6-7]简要介绍了CRTS III型板式无砟轨道的结构特点, 重点介绍了CRTS Ⅲ型板式无砟轨道裂缝的成因、裂缝的特征及裂缝的防治措施。ZHOU等[8]针对高速铁路CRTS III型板式无砟轨道在温度作用下的变形，建立了CRTS III型板式无砟轨道温度场和变形的仿真模型，并通过现场试验进行了验证。ZENG等[9-13]建立了CRTS III型板式无砟轨道系统有限元数值模型，重点研究CRTS III型板式无砟轨道系统中自密实混凝土填充层在重载列车作用下的疲劳特征。LI等[14-15]对CRTS III型板式无砟轨道的混凝土性能展开了试验研究，对加入聚羧酸型减水剂的混凝土的抗压强度、弹性模量和抗冻性进行了分析，结果表明减水剂对混凝土的性能具有显著影响。SHENG等[16]对CRTS III型板式无砟轨道进行了有限元分析，得到了弹性垫板在使用过程中的应力分布规律，并根据有限元分析结果，设计并开展了弹性垫板试件的静、动、疲劳试验。结论如下：在正常使用过程中，弹性垫板的应力水平较低，可认为弹性垫板仍处于线弹性阶段。弹性垫板的材料性能可以用等效弹性模量来表征，通过实验研究确定其等效弹性模量为0.6 MPa。MA等[17-19]利用自行设计的预压装置，重点研究了在冻融循环和荷载耦合作用下自密实混凝土填充层的性能演变机制和损伤本构模型。曾志平等[20-21]建立了CRTS Ⅲ型板式无砟轨道结构1∶1足尺试验模型，开展了30 t轴重列车作用下轨道结构力学特性试验，获得了800万次疲劳试验后轨道结构力学性能演化特征。LIU等[22]在二维车辆-轨道-桥梁耦合模型的基础上，提出了一种频域车辆-轨道耦合模型，并利用动态柔度法确定车辆-轨道系统的动态柔度。PENG等[23]提出了一个模型，用于预测CRTS III型板式无砟轨道在简谐荷载作用下产生的地面振动。XU等[24]建立了高速列车-CRTS III型板式无砟轨道-路基的耦合动力学模型。利用该模型，从理论上研究和分析了在光滑和随机轨道不平顺条件下，车辆数量对列车-CRTS III型板式无砟轨道-路基耦合系统动态特性的影响。目前，关于CRTS Ⅲ型板式无砟轨道隔离层关键构件-弹性垫板力学性能的研究尚不多见。轨道板和自密实混凝土填充层之间通过2排U形钢筋及新旧混凝土的高黏性形成共同受力的复合板，复合板通过凸台将上部结构传来的纵、横向力传递给铺设在凹槽周围的弹性垫板，弹性垫板通过自身压缩变形达到减震耗能的目的[25]。弹性垫板作为自密实混凝土填充层和底座板之间的缓冲构件，对高速列车的行车安全性和乘坐舒适性影响显著。为研究CRTS Ⅲ型板式无砟轨道在服役过程中弹性垫板的受力特性，开展弹性垫板的平面压缩试验，探究不同截面尺寸及不同厚度情况下弹性垫板试件的荷载-位移曲线变化规律，揭示弹性垫板的尺寸效应，并拟合出一个考虑尺寸效应的荷载-位移力学模型，利用该力学模型与试验数据进行对比。结果表明：本文所提出的荷载-位移力学模型与弹性垫板平面压缩的试验数据吻合良好，该力学模型可为高速铁路列车-CRTS Ⅲ型板式无砟轨道-简支梁桥系统的建立提供参数依据，可为弹性垫板材料缩尺模型试验的相关设计提供参考。

1 CRTS Ⅲ型板式无砟轨道弹性垫板

高速铁路列车-CRTS Ⅲ型板式无砟轨道-简支梁桥系统如图1所示，其中CRTS Ⅲ型板式无砟轨道由3层混凝土板组成，从上至下分别为：双向预应力混凝土轨道板(C60)、自密实混凝土填充层(C40)、混凝土底座板(C40)。轨道板和自密实混凝土填充层之间通过2排U形钢筋及新旧混凝土的高黏性形成共同受力的复合板，复合板与底座板之间通过铺设4 mm厚的土工布形成隔离层，该隔离层的存在使得复合板和底座板之间在竖向上抗压不抗拉。每个底座板设置2个凹槽，凹槽截面为1 000 mm×700 mm的矩形，槽深100 mm。自密实混凝土填充层采用现场浇筑的方式，浇筑过程中使得自密实混凝土填充层下部对应底座板凹槽位置处形成2个限位凸台，自密实混凝土填充层与底座板之间通过这两组凸台-凹槽的嵌固作用达到限位的目的。底座板与梁体通过预埋钢筋紧密相连。当梁体因基础沉降，地震作用等外部环境影响发生竖向变形时，底座板将会在预埋钢筋及自重作用下与复合板脱离，使得底座板与复合板之间出现脱空区域，此脱空区域将会对高速行驶的列车产生一定的激扰，影响乘车舒适性，严重时影响行车安全性；复合板通过凸台将上部结构传来的纵、横向力传递给铺设在凹槽周围的弹性垫板，弹性垫板通过压缩变形达到减震耗能的目的。

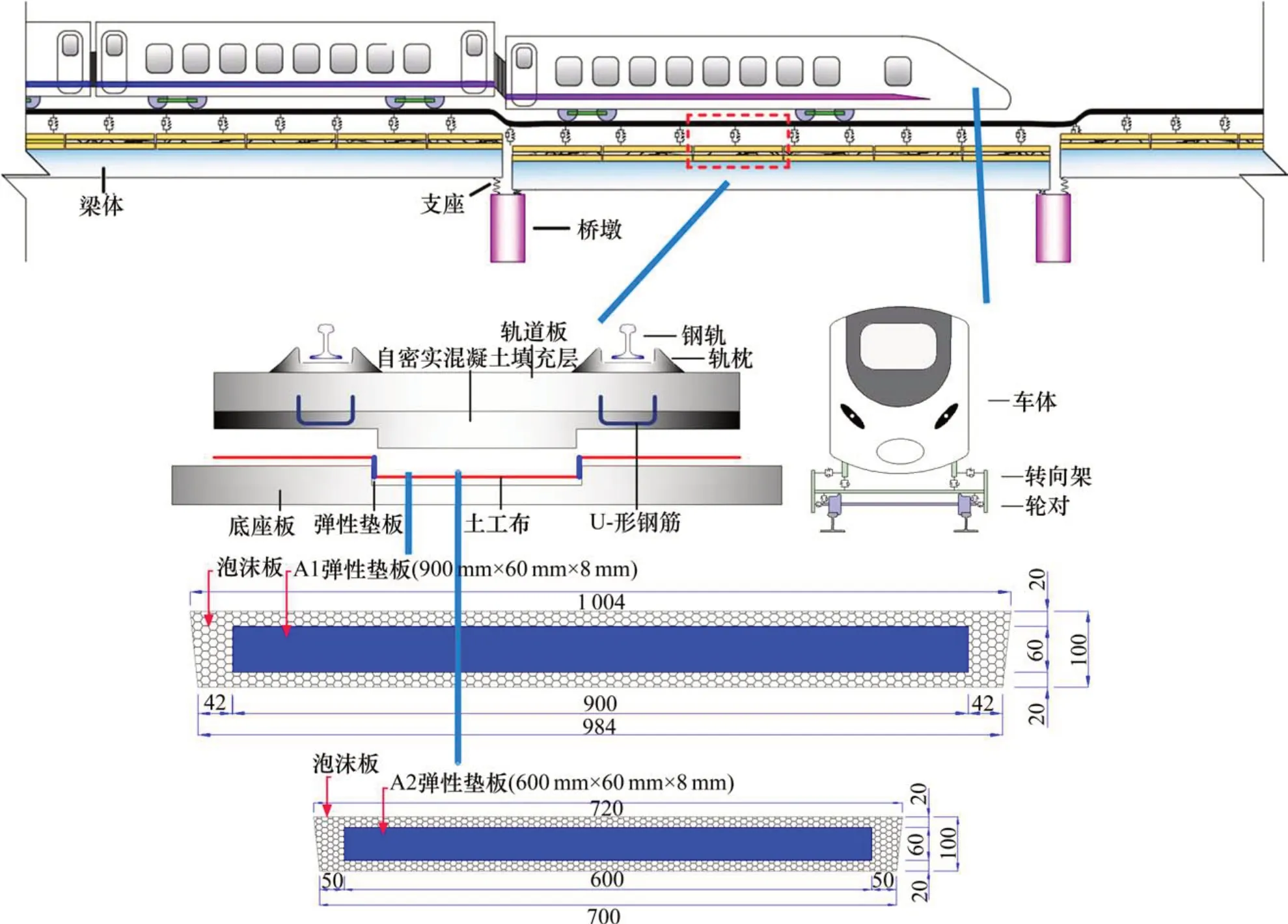
图1 高速铁路列车-CRTS Ⅲ型板式无砟轨道-简支梁桥系统示意图Fig. 1 Schematic diagram of train-CRTS Ⅲ SBT-simply-supported bridge system

综上可知，复合板和钢轨之间通过扣件连接，底座板和桥梁之间通过预埋钢筋连接，而复合板和底座板之间的层间关系较为复杂，且分析研究较少。复合板和底座板之间的层间关系对CRTS Ⅲ型板式无砟轨道受力特性和耗能能力具有显著影响，探究复合板和底座板之间的层间关系对CRTSⅢ型板式无砟轨道自身的受力特性和耗能能力具有重要意义，对探究高速铁路CRTS Ⅲ型板式无砟轨道-桥梁系统的研究具有理论意义。通过分析CRTS Ⅲ型板式无砟轨道结构特点可知，复合板和底座板之间在竖向上没有连接作用，可看作是抗拉刚度为0，抗压刚度无穷大的弹簧单元；在纵、横向上可视为抗拉和抗压刚度一致的弹簧单元，该弹簧单元的刚度为弹性缓冲垫层的抗压刚度与土工布摩擦作用结合之后的等效刚度，目前关于该等效刚度的研究尚未见报道。因此，探究弹性缓冲垫层在平面压缩时的刚度对与CRTS Ⅲ 型板式无砟轨道相关的科学研究具有重要的理论意义。

如图2所示，凹槽四周铺设8 mm厚弹性垫板，弹性垫板中间部分材质为三元乙丙橡胶，外围一圈为泡沫板。设置在凸台-凹槽之间的弹性垫板是为了传递上部结构的纵横向载荷，缓冲作用在凸台-凹槽上的纵横向力；降低温度和混凝土收缩徐变产生的约束力，以弥补刚性材料的不足。标准弹性垫板的厚度为8 mm。铺设在凹槽四周弹性垫板的标准尺寸有2种，A1型弹性垫板尺寸为：900 mm×600 mm×8 mm；A2型弹性垫板尺寸为：600 mm×600 mm×8 mm，表1和表2分别是弹性垫板材料性能参数及泡沫板的材料性能参数。

表1 弹性垫板材料性能参数Table 1 Material parameters of rubber pad

表2 泡沫板材料性能参数Table 2 Material parameters of high-strength extruded sheet

图2 CRTS Ⅲ型板式无砟轨道弹性垫板Fig. 2 CRTS Ⅲ SBT rubber pad

2 试验

2.1 试验设计

为探究CRTS Ⅲ型板式无砟轨道弹性垫板在平面压缩时的荷载-位移关系，计划对A1型及A2型弹性垫板进行平面压缩实验，获得A1型及A2型弹性垫板在平面压缩时的荷载-位移关系。然而，由于A1型及A2型弹性垫板在长度方向上长达1 m，常规加载装置无法进行加载。考虑到弹性垫板材质具有明显尺寸效应，故可以设计一组方便加载的小尺寸试件进行平面压缩试验，通过分析该组小尺寸试件荷载-位移曲线间的规律，探究该组小

由于尺寸效应不仅和截面尺寸有关，和试件厚度也有很大关系。因此，为探索弹性垫板的尺寸效应规律，获得A1型及A2型弹性垫板在平面压缩时的荷载-位移关系，设计了5组弹性垫板试件，进行弹性垫板的平面压缩试验，试件设计如表3所示。尺寸试件的尺寸效应，进而推导出A1型及A2型弹性垫板的荷载-位移关系。同时，探究所得的弹性垫板的尺寸效应规律可为CRTS Ⅲ型板式无砟轨道弹性垫板的优化设计提供参考。

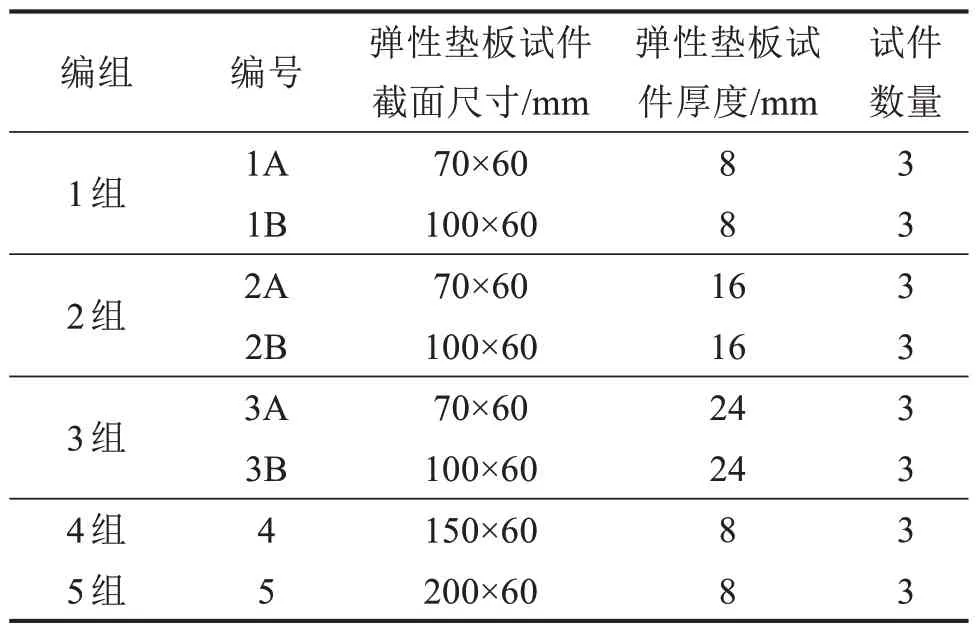
表3 弹性垫板试件设计Table 3 Design of rubber pad specimens

2.2 试件制作与加载

从厂家购买A1型弹性垫板5个，按照设计尺寸进行切割。由于A1型弹性垫板标准厚度为8 mm，因此16 mm，24 mm及32 mm厚弹性垫板试件分别是由2个，3个及4个8 mm厚的弹性垫板粘结得到，部分弹性垫板试件如图3所示。

图3 CRTS Ⅲ型板式无砟轨道弹性垫板试件Fig. 3 Rubber pad specimens of CRTS Ⅲ SBT

本试验在中南大学高速铁路建造技术国家工程实验室中进行。加载装置为万能材料试验机，按照等荷载步的加载准则进行加载。试验过程中，荷载和位移同步采集。如图4所示，提前在万能材料试验机的计算机控制端输入加载过程，然后将制作好的弹性垫板试件放到万能材料试验机的加载端，开启加载。万能材料试验机采用伺服电机驱动系统传动横梁上下移动，实现加载过程。弹性垫板试件在横梁下降过程中，受到上下两钢板的挤压作用从而达到平面压缩的目的。弹性垫板试件的变形由万能材料试验机的数据采集系统进行采集，力和位移数据统一由万能材料试验机的计算机导出。

图4 CRTS Ⅲ型板式无砟轨道弹性垫板试件加载过程Fig. 4 Loading process of CRTS Ⅲ SBT rubber pad specimen

3 试验分析

3.1 试验现象

加载后的弹性垫板试件形态相似，由于篇幅的限制，本文仅讨论3A弹性垫板试件及3B弹性垫板试件加载后的形态，3A弹性垫板试件及3B弹性垫板试件加载后的形态如图5所示。

图5 CRTS Ⅲ型板式无砟轨道弹性垫板试件加载后形态Fig. 5 Shape of CRTS Ⅲ SBT rubber pad specimen after loading

由图5可以看出，由多层标准弹性垫板胶结而成的试件，如3A弹性垫板试件(厚度为24 mm)及3B弹性垫板试件(厚度为24 mm)，在平面压缩过程中，每一层均发生压缩变形，每一层压缩变形量几乎一致；随着加载力的增大，弹性垫板试件压缩变形量增大，截面面积变大，厚度减小；卸载之后，弹性垫板试件截面面积减小，变形恢复较快，且每层恢复速度不完全一致。对3A及3B弹性垫板试件而言，上下两层恢复较快，中间一层恢复较慢；对2A及2B而言，加载时弹性垫板试件两层同时发生压缩变形，截面面积增大，压缩变形量几乎一致；卸载时，2层恢复速度几乎一致；对1A，1B，4及5等仅有1层的标准厚度弹性垫板试件而言，加载时压缩变形量随着荷载的增大逐渐增大，截面面积增大，厚度减小；卸载时，截面面积有所恢复，压缩变形量有所回弹。以上所有弹性垫板试件在卸载之后压缩变形量均有所回弹，但回弹量均较小。

3.2 荷载-位移曲线

根据弹性垫板试件的材料特性试验数据(每种型号有3个试件，取3个试件所测数据的平均值)可得图6所示弹性垫板试件荷载-位移曲线。图6(a)是厚度均为8 mm，截面尺寸不同的弹性垫板试件的荷载-位移曲线，图6(b)是截面尺寸均为70 mm×60 mm，厚度分别为8，16及24 mm的弹性垫板试件的荷载-位移曲线，图6(c)是截面尺寸均为100 mm×60 mm，厚度分别为8，16及24 mm的弹性垫板试件的荷载-位移曲线。

图6 CRTS Ⅲ型板式无砟轨道弹性垫板试件荷载-位移曲线Fig. 6 Load-displacement curves of rubber pad specimens of CRTS III SBT

从图6可以看出，所有弹性垫板试件的荷载-位移曲线形状大体一致，均随着荷载的增加，位移不断增大，且位移增大幅度越来越小。图6(a)可以看出，厚度相同，截面不同的4组弹性垫板试件的荷载-位移曲线并不重合，相同荷载情况下，截面积越大，位移越小。图6(b)可以看出，截面尺寸均为70 mm×60 mm，厚度分别为8，16及24 mm的弹性垫板试件的荷载-位移曲线相差较大，荷载相同情况下，弹性垫板试件越厚，其位移越大。同理，从图6(c)可以看出，截面尺寸均为100 mm×60 mm，厚度不同的弹性垫板试件的荷载-位移曲线有显著差异，荷载相同情况下，弹性垫板试件越厚，其位移越大。

3.3 割线刚度分析

通过分析弹性垫板试件的割线刚度随尺寸的变化规律来研究弹性垫板试件的尺寸效应。假设第i次加载时的峰值点荷载值为Pi，相应的峰值点位移值为δi，则试件的割线刚度可表示为：

图7为弹性垫板试件割线刚度K随试件截面面积及厚度变化的规律图。由图7(a)可知，弹性垫板试件厚度相同时，随着截面面积的增大，其割线刚度不断增大；同一个试件随着加载力的增大，其割线刚度呈线性增大。由图7(b)及7(c)可知，弹性垫板试件截面面积相同时，随着厚度的增大，试件割线刚度逐渐减小；同一个试件随着加载力的增大，割线刚度呈线性增大。这说明弹性垫板试件的割线刚度与截面面积、厚度及加载力有关。截面面积越大，厚度越小，其割线刚度就越大。以上分析均说明弹性垫板试件的力学特性具有明显的尺寸效应，截面面积越大，厚度越小，割线刚度越大，平面可压缩性越低。

图7 CRTS Ⅲ型板式无砟轨道弹性垫板试件割线刚度Fig. 7 Secant stiffness of rubber pad specimens of CRTS III SBT

4 考虑尺寸效应的弹性垫板荷载-位移力学模型

从图6可以看出，弹性垫板截面面积和厚度对荷载-位移曲线有显著影响，弹性垫板试件的截面面积越小，厚度越大，弹性垫板试件越容易变形。弹性垫板的荷载-位移曲线采用二次多项式近似表示为：

其中：φ为弹性垫板形状系数；a，b分别为弹性垫板截面的长和宽，已知b=60 mm，β1，β2，β3，β4分别为待定系数。令：

故，弹性垫板荷载-位移函数可表示为：

利用MATLAB软件中多元曲线拟合工具箱，拟合结果如图9所示。蓝色曲面是拟合函数，黑色散点是弹性垫板实测数据点。求得4个待定系数分别为β1=1.47，β2=0.04，β3=-0.93，β4=3.62，即弹性垫板荷载-位移曲线函数表达式为：

任取2条弹性垫板试件荷载-位移曲线验证此荷载-位移力学模型的准确度。选取1B和3B 2种弹性垫板试件，将这2种弹性垫板试件的实测数据点和荷载-位移力学模型计算结果绘制在同一图形中，如图9所示。由图9可以看出弹性垫板荷载-位移力学模型计算结果与弹性垫板平面压缩试验数据所得荷载-位移曲线吻合良好。说明此荷载-位移力学模型可以准确表示弹性垫板的荷载-位移关系。

图8 荷载-位移力学模型拟合Fig. 8 Load-displacement mechanical model fitting

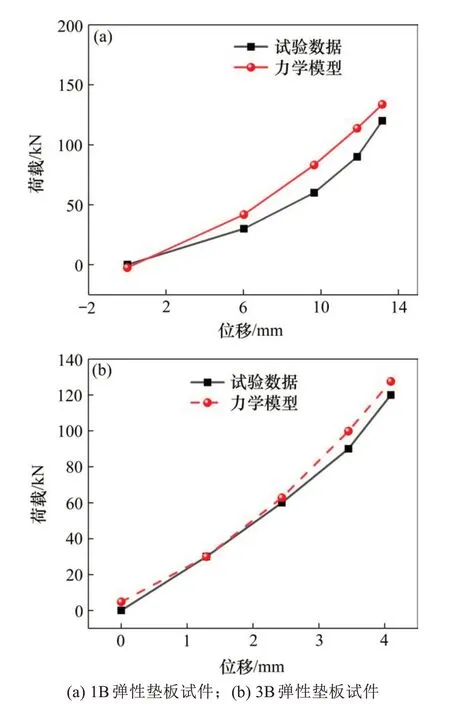
图9 弹性垫板试件荷载-位移力学模型拟合效果验证Fig. 9 Verification of fitting effect of load-displacement mechanical model of rubber pad specimens

考虑尺寸效应的弹性垫板荷载-位移力学模型可以用来表示截面宽度为60 mm，截面长度和厚度任意的弹性垫板的荷载-位移关系。因此可以通过此荷载-位移力学模型推算出A1型及A2型弹性垫层的荷载-位移关系曲线，对进一步推导CRTS Ⅲ型板式无砟轨道复合板和底座板的层间关系提供参考，为弹性垫板的本构关系及高速铁路列车-CRTS Ⅲ型板式无砟轨道-简支梁桥系统的建立提供参数依据。

5 结论

1) 不同型号的弹性垫板试件的荷载-位移曲线形状大体一致，均表现为位移随着荷载的增加而不断增大，且位移增大幅度越来越小，曲线形状呈抛物线形。

2) 弹性垫板试件的割线刚度随加载力的增大呈线性增大；弹性垫板试件厚度相同时，其割线刚度随截面面积的增大而增大；弹性垫板试件截面面积相同时，其割线刚度随厚度的增大而逐渐减小。

3) 在考虑尺寸效应的基础上利用二次多项式拟合出弹性垫板荷载-位移力学模型，模型计算结果与试验数据吻合良好，说明该荷载-位移力学模型可为弹性垫板的本构关系及高速铁路列车-CRTS Ⅲ型板式无砟轨道-简支梁桥系统的建立提供参数依据。