《多边形的面积》整理和复习策略
□ 广东省广州市从化区街口街团星小学 欧阳伯祥
在多边形面积复习课教学过程中,教师的目的是让学生能够把握不同多边形的内在联系,运用多边形面积计算方法来解决图形问题。基于此,在新媒体和互联网技术的帮助下,学生通过小组学习的形式,感知图形的运动变化,实现自主认知的建构。在整理和复习中运用动态几何的观点,学生体会多边形图形之间是可以相互转化的,多边形图形面积公式是可以相互沟通的,让学生将所学的多边形图形的面积公式整合统一,形成系统,让学生识“变”,会“变”,用“变”,“变”出别样精彩。
一、在情境中重现,变在开始时
复习课展开的重要前提,是将多边形面积公式进行情境化重现。在多边形复习课教学中,教师要引导学生对头脑中点状的知识进行整理,情境重现,从而形成体系;同时,要善于抓住学生容易忽略、错误的区域,重点弥补,让学生学得更完整。同一课堂情境中,新的教学生成是重要的突破点,教师应有意识地捕捉有价值的新生成,借此让学生在交流和思考中对数学本质进行内化,激活学生的数学方法、意识、思想。本课的导入环节如下:
师:同学们,从PPT上看到了哪些图形?生:长方形、正方形、平行四边形、三角形、梯形。
师:会连吗?生:长方形s=ab、正方形s=a2、平行四边形 s=ah、三角形 s=ah÷2、梯形 s=(a+b)h÷2。
PPT配合学生回答连线。PPT呈现连线后,再按图形顺序公式一一对应图形。
然后提问:这些面积计算公式是怎样推导出来的?结合学生的回忆,追问:推导过程有什么共同之处?它们之间有什么联系吗?结合学生的汇报,适时点拨。在这样的纯数学情境中,学生重温了多边形面积的公式推导,唤醒学生原有的知识积累,以期学生在更快的时间内展开思维,进行深度理解和思考。
二、在梳理中重构,变在形成中
原本零散呈现的知识,在教师创设的问题情境中得到了激活,加上适时地梳理和沟通,将呈现温故而知新之境。多边形面积的单元复习有别于新授和练习,它侧重于让学生实现几何知识内在结构联系的新整合和再“生长”,从而达到培养学生数学核心素养的要求。过程中,把教材教厚,把知识变实是基础,让知识再“开花”是拓展,是升华。
在梳理环节中,引导学生梳理出平行四边形、三角形、梯形的面积公式,通过点拨、思考、内化,学生明白这些均由已学的图形变形转化得到的。体会不同多边形之间的内在联系,且它们是可相互转化的,变在形成中。
生:没想到以前学过的几个面积公式是可以由梯形的面积公式转化而来,我感受到了数学的千变万化。
师:是的,转化。(板书:转化)利用转化,解决某一数学问题时,我们可以将未知的信息转化为已知的条件。学习数学最重要的思想就是“化新为旧”“化繁为简”“化难为易”。
师:在这个单元中,我们按顺序先后认识了平行四边形面积、三角形和梯形的面积计算公式。你是怎样推导平行四边形面积公式的?生:通过割补。
师:把平行四边形转化成长方形。(配合PPT呈现,师黑板贴图)
师:那如何推导三角形面积计算公式?生:两个相同的三角形拼成一个平行四边形,算出平行四边形的面积之后除以2就是一个三角形的面积。
师:把三角形转化成平行四边形。(PPT配合,师黑板贴图)
师:梯形面积公式呢?如何推导?生:两个相同的梯形拼成一个平行四边形。
(PPT配合)
师:无论是计算长方形面积还是计算平行四边形面积,我们用的方法都是数方格。数小方格,实际上是数面积单位。其实,计算所有图形的面积的本质都是数面积单位。
三、对比中提升,变在本质上
教学中,教师先将几何图形放在方格纸上观察、比较、思考、感悟,再用几何画板分别展示梯形的上底、下底缩短和变长的过程,可以变成三角形、平行四边形、长方形、正方形,丰富了学生的认知,学生的知识面也在这个过程中得到了拓展。
师:通过回顾这些图形面积计算方法,我们更加清楚了它们之间的联系。这些图形的面积你会算吗?
PPT补充:小方格均为正方形,边长是1cm,每个方格表示1cm²。
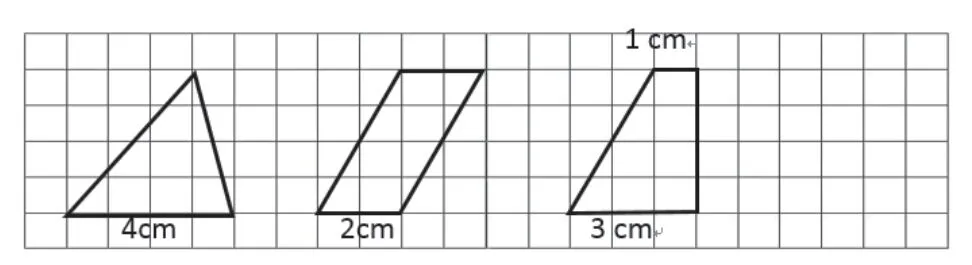
图1
( )cm² ( )cm² ( )cm²
生: ① 4×4÷2=8, ② 2×4=8, ③(1+3)×4÷2=8
师:同一幅图中的三个不同的图形,为什么面积都是8cm²?生根据学习单小组研究并讨论后汇报,生:底和高不变。
教师根据学生回答后再酌情总结。
(PPT呈现题目,可动态呈现图形点、边的移动改变过程)你还会算吗?
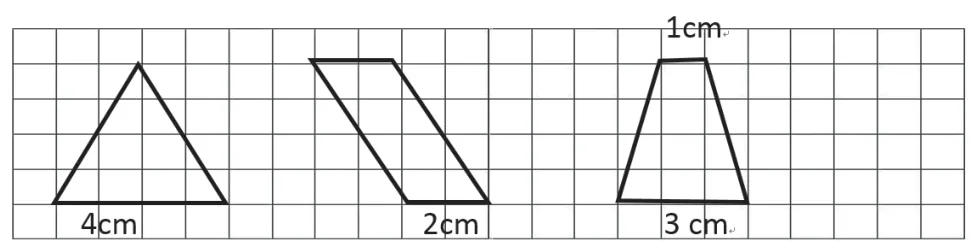
图2
( )cm² ( )cm² ( )cm²
生: ① 4×4÷2=8, ② 2×4=8, ③(1+3)×4÷2=8
师:(PPT呈现)点、边的位置发生变化,为什么面积都是8cm²?生:形状改变,但底和高不变。
教师抛出问题:“看来图形间是有联系的,你能用连线的方式表示这种推导关系吗?”在重构整合中,学生对各线知识的紧密联系有全新的理解。之后,教师要使用“添加剂”—精心设计的复习资源,将知识彼此间建立关联、融会贯通。学生在这些复习资源的辅助下,能够形成数学知识系与知识域,才能够在学习中丰富认识并达到再“生长”的目的。
接着,教师抛出更高层次的问题:“像这样,面积和高都不变的图形还有吗?不妨转换角度研究,将梯形、三角形、长方形这三种图形的面积公式联系起来。如何联系呢?利用极限思想,寻找变量。对比三个公式我们不难发现,变化的地方是底边的变化,梯形有上底和下底,三角形仅有一个底,而长方形的是长(上下两个长);不变的是都有高(长方形是宽)。那么,我们就可以选择梯形的一个底当作变量,比如:我们选择上底为变量,将上底趋近于0,也就是上底没有了,此时梯形就变成了三角形。”如图所示。
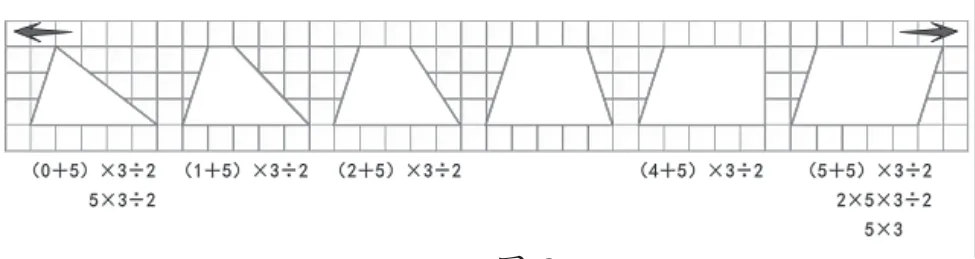
图3
通过梯形上底的变形,使得原来孤立的知识更加连贯系统,从而培养学生“相互转化、相互依存”的数学思维,变在本质里。
四、在情境中拓展,变在应用中
在数学多边形复习课中,需要针对性的练习来检测复习效果。通过重现旧知、梳理重构、对比提升,为多样化的问题以及问题之间的联结和转换提供了条件,从而实现迁移应用,达到解决问题的目的。如果简单的学习材料有不简单的教学设计,可以让一道题发挥最大的教学功能。引学生思考,让学生的思维活跃起来,同时也让这堂复习课“开花”。
请计算下面图形的面积。(PPT出示教材中第103页第2题)
师:(1)请打开学习单,先认真审题后互相讨论一下解题思路,再独立完成。过程中,如有问题,小组内互相交流、指导。
(2)完成后个别汇报。
(3)请同学们评价。
(4)总结方法:做这类题目有什么技巧,注意什么?(生:利用分割法,注意计算要小心。)
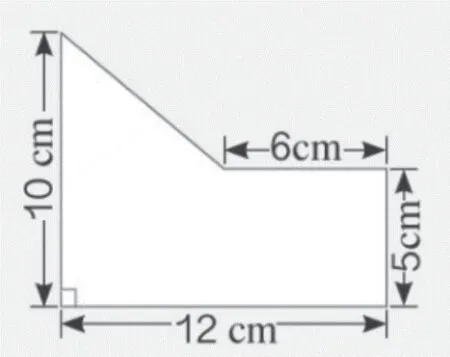
图4
师:掌握不错,我们继续挑战难度。
(PPT出示题目)如图:梯形、平行四边形、三角形的面积相等。求平行四边形的底和三角形的底。(单位:cm)
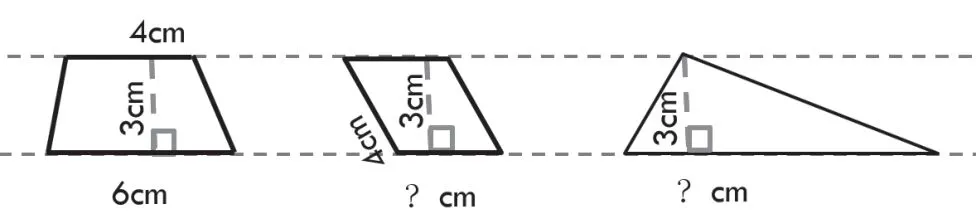
图5
师:(1)请打开学习单,先认真审题。
(2)学生自主完成,教师巡堂中发现部分学生不懂如何求平行四边形的底和三角形的底。如果遇到困难,引导学生发挥小组作用,请小组内互相交流,互相指导帮助,提示:这道题的关键句是哪一句?
(3)完成后个别小组汇报。(汇报出解题过程及解题依据)学生汇报时,让学生出示第二种方法,用红笔标注上下底并标上数据。若出现底的单位错误,教师提示:底是长度单位,立即纠正。若没有出现第二种方法,教师进行提示引导:还有其他方法吗?
(4)请同学们评价。
(5)总结方法:你们发现什么?提示发现规律。
(6)同学们做对的请举手,鼓励全体。
估算不规则图形的面积:每个方格表示1km²。
(PPT出示题目)估一估,从化温泉镇的面积不超过( )平方千米。
师 :(1)请同学们观察图形,分析题目,“不超过”是什么意思?(生:要估大数据。)估算温泉镇的面积有什么方法?(生:①数方格;②看成三角形来计算。)
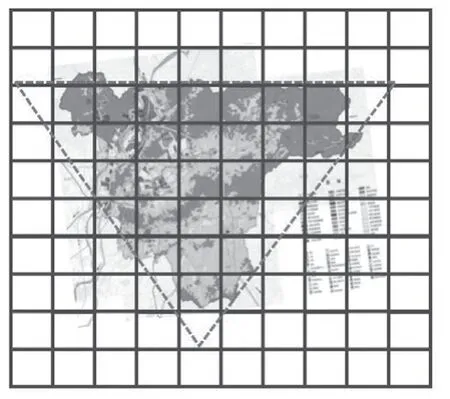
图6
(2)独立完成,教师巡视,在完成的过程中,如果遇到困难,请小组内互相交流,互相指导。
(3)完成后个别汇报。
(4)请同学们评价。
(5)总结方法:做这类题目有什么技巧,注意什么?(生:利用分割法,注意计算要小心。)
(6)同学们做对的请举手,鼓励全体。
学生在复习中不断变化和成长,以此为基,教师拉动图形,使其不断变化,让学生在观察图形的变化中,感悟了内在联系以及图形的本质。最后,在应用时,梯形面积计算公式成了百变应用公式。
五、在总结中提升:变在“归一”中
数往知来,温习旧知,收获新知。变发生在复习时,变存在于梳理中。数学,“数”是本源,形而上“学”,教学中要“追其本,溯其源,引其思,扎其根”,“变”而不变。
1.求通
回顾整个小学阶段数学的学习,不难发现,学生日常所学的知识是零碎的,开始阶段只是将所学的平行四边形、三角形和梯形(或者加上三年级所学的长方形、正方形)的面积计算公式进行了简单的罗列,它们都是独立存在的,各图形之间没有建立起联系。通过问题引领使之系统化、条理化、清晰化,形成较为完善的认知结构。
2.求构
借助前测中多种形式的梳理,在对比中提升,构建一个网络。如上所述,除了具体的知识点,还需以能够连接整个知识的核心点,如教材的序列、转换思想等,以此作为立足点,进一步引导学生探索知识之间的内在关系,让学生反思知识点,形成知识链,以思考导向形式将发展变化的知识链结成一个知识网络,构建脉络清晰的知识板块。这种深入的结构性的思考导向,不仅是重建知识的脉络,更是重构学生的思考方式。求构就是以结构性的知识网络来促成对知识价值的深入理解。
3.求悟
在原来的知识网络上,再进一步创新性利用知识的共同点,直达学生的数学思想本质,从特殊到一般规律,举一反三。最后在基础练习中,变一变,可以有不同的应用,不同思维层次的孩子都有发挥的空间,动态地感受知识本质之间的关联,进一步体会转化思想,为将来的几何学习夯实基础,培养数学思想。
总之,复习是师生、生生互相交流、回忆、梳理、纠错、提升的过程。基于知识网下的结构性重建复习,能以一种超脱的姿态助力学生广度、深度的悟得。这样的几何复习课,除了要做“理”,把知识“纵成链”“联成网”再升华“凝成线”从而让学生识“变”,用“变”和会“变”,变出精彩。

