基于ASTEC程序的反应堆严重事故下压力容器下封头传热分析
左嘉旭 宋 维 安婕铷 庄少欣 石兴伟
1(生态环境部核与辐射安全中心 北京 100082)
2(国家环境保护核与辐射安全审评模拟分析与验证重点实验室 北京 100082)
根据《核动力厂设计安全规定》(HAF102)中的要求[1],核电厂在设计中除了设计基准事故,还必须考虑核动力厂的超设计基准事故,包括选定的严重事故。关于严重事故现象的分析和缓解措施的研究日益重要[2-5],其中在压力容器外设置注入冷却水的系统是用以实现严重事故工况下的反应堆压力容器内熔融物滞留(In-Vessel Retention,IVR)的关键缓解措施之一。该系统使冷却水流过反应堆压力容器与保温层间的通道,通过反应堆压力容器下封头外壁面与冷却水的换热,带走堆芯熔融物释放出的热量,维持反应堆压力容器的完整性。
针对IVR措施的有效性评价,压力容器外壁面的传热性能、流体流动性能、堆内熔融物熔池的结构和组成等问题是重点关注内容,也有很多相关研究。有研究结果表明:熔融物达到稳定分层结构下,熔池对压力容器壁面施加的热负荷直接决定压力容器下封头完整性[6-9]。因此,评估IVR措施有效性的关键是分析其是否发生热工失效,即下封头内熔融池作用于压力容器的最终稳态热负荷不超过其外壁面沸腾换热的临界热流密度(Critical Heat Flux,CHF)[2-3,9-10]。同时,下封头结构的完整性是IVR成功的前提,需论证在最终稳态热负荷状态下不发生结构失效,即下封头剩余壁厚能够实现熔融物的承载,因此下封头在熔融物熔蚀后剩余厚度具有重要意义,也是判断IVR是否有效的重要依据之一。业界普遍认为如果能够保证良好的冷却,就可以在确保压力容器剩余厚度和其结构完整。目前IVR有效性评估会对其厚度进行简单分析并确定极限值,但是应用程序进行系统性计算较少。因此,本文应用ASTEC严重事故系统分析程序,以压力容器厚度和其分布为目标,进行系统性分析计算,评估其剩余厚度和IVR有效性,对未来商业运行核电堆型中IVR有效性评估具有借鉴意义,同时也对我国严重事故程序的验证提供模型对比和技术支持。
1 ASTEC计算程序和模型
法国核防护与安全研究院(Institute for Radiological Protection and Nuclear Safety,IRSN)与德国核设施与安全研究中心(Gesellschaft für Anlagen- und Reaktorsicherheit,GRS)联合开发了严重事故一体化分析程序ASTEC,主要用于模拟压水堆严重事故过程和现象。ASTEC涵盖的主要严重事故现象包括:堆芯降级和堆芯熔化、燃料与冷却剂相互作用、回路热工水力、熔融物与混凝土相互作用、安全壳内热工水力、气溶胶和裂变产物的输运等。ASTEC中主要的计算模块包括:用于计算堆内堆芯降级和熔化的ICARE模块;用于计算系统回路的热工水力的CESAR模块;用于计算熔融物与混凝土相互作用的MEDICIS模块;用于计算裂变产物及气溶胶输运的SOPHAEROS模块;用于计算放射性同位素衰变行为的ISODOP模块;用于模拟安全壳中的瞬时虚拟燃烧的COVI模块;用于计算安全壳热工水力的CPA模块等[11]。
ASTEC程序中对于压力容器内下腔室传热计算可考虑熔融物分层、熔融物与下封头内壁面等不同反应堆结构之间的导热、对流换热和辐射换热等换热模式。其中,熔融物和下封头内壁面之间的换热模型对于压力容器下封头传热计算分析最重要。在ASTEC中熔融物与下封头内壁面的换热系数的计算过程中可以考虑两种情况,第一种是熔融物内含有能够产生衰变热的裂变产物,则采用BALI换热关系式;第二种是熔融物内不含有能够产生衰变热的裂变产物,则采用CHAWLA-CHAN换热关系式[12-13]。
压力容器轴向自下而上包括下封头、过渡段、筒体,在综合兼顾计算精度和计算速度的基础上进行节点划分并建模,节点划分如图1(a)所示,其中轴向方向将下封头划分为20节点;过渡段划分为5节点;筒体划分为20节点;径向方向将压力容器下封头和过渡段壁面统一划分为10层,由内向外第1~第10层;筒体划分为两层,如图1(b)所示。
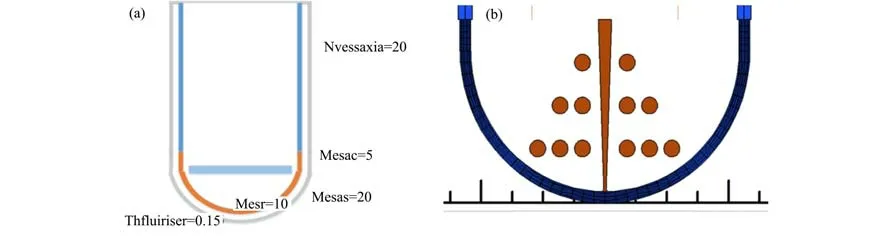
图1 压力容器节点划分示意图 (a) 压力容器轴向方向节点划分,(b) 下封头径向方向节点划分Fig.1 The module division of reactor pressure vessel (a) The nodalization in axial direction of pressure vessel, (b) The nodalization in radial direction of lower head
将压力容器内熔融物作为条件边界进行输入,主要假设各种熔融物组分的质量和氧化份额,并选取典型的中破口事故序列,并取其衰变功率平均值21 MW作为计算的衰变功率。选择IVR保温层流道通过专用泵以450 m3·h-1的流量向IVR注水,注水温度为40 ℃。安全壳壁面为绝热壁面,不考虑喷淋和安全壳内部热量的导出,其压力为0.1~0.2 MPa,温度为50 ℃。综合已有堆型计算分析的经验,结合大型先进压水堆的设计,将本研究中熔融物组分和质 量 分 别 假 设 为:UO2,92 353.29 kg;Fe,约43 000 kg;Zr,23 133.9 kg;Zr氧化份额,41.8%。由于直接假设了熔融物的衰变功率,因此在熔融物与下封头内壁面的换热系数的计算过程采用CHAWLA-CHAN换热关系式,而熔融物上部与空气对流换热为Kobayashi关系式[14]。
已有的研究中表明,内部熔融物为两层结构情况下,下封头的失效时间最短,因此熔融物分层结构选择两层开展分析[15]。
2 ASTEC计算分析
IVR使用冷却水流过反应堆压力容器下封头外表面的流道,带走堆芯熔融物释放出的热量,以维持反应堆压力容器的完整性。应用ASTEC严重事故一体化程序,在10 000 s时刻左右,下腔室熔融物形成两层稳定熔池后,就下封头外壁面换热参数、下封头传热、下封头壁厚等安全相关的关键问题进行计算分析,进而从热工性质和下封头结构两方面分析IVR的有效性。
两层稳定熔池的底部为重金属氧化层,上部为金属层,各层混合温度分别约为2 700 K和2 200 K,如图2所示。熔池形成后,其中金属层厚度分布稳定在0.80~0.85 m之间,而氧化层厚度分布稳定在1.52~1.57 m之间,图3为熔融物各层的厚度。
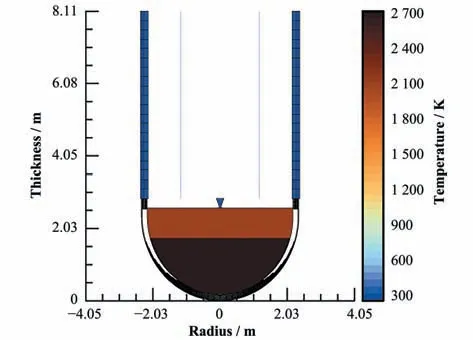
图2 熔融物分层及温度Fig.2 The melt stratification and the temperature
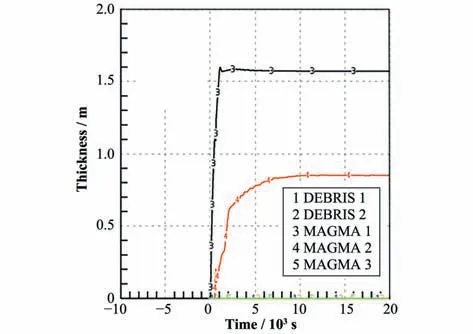
图3 熔融物各层厚度分布Fig.3 The thickness distribution of each layer of melt stratification
2.1 下封头外壁面换热参数
在IVR中,对下封头完整性的评估主要通过临界热流密度的情况来确定,换热功率小于临界热流密度是下封头完整性得到保证的最关键因素之一。下封头外壁面的液相速度、空泡份额和流体温度对于临界热流密度具有较大影响,而且不同位置的临界热流密度也不同。选择不同节点,对滞留堆芯熔融物的下封头外壁面的液相速度、空泡份额和温度等进行计算。分析换热过程中影响临界热流密度的关键参数的变化。
液相速度选择了第05、10、15、20节点,由于05节点靠近底部,截面面积相对较小,所以流速在选择的4个节点中最大。4个观测节点中,最大流速是最小流速的2.3倍,符合05节点在底部,20节点在下封头上部的分布情况,如图4所示。

图4 下封头节点液相流速Fig.4 The liquid flow rate of selected nodes in the lower head
空泡份额自下而上选取了第09、18、27、36、45节点的计算值进行分析。如图5所示,其中18节点的空泡份额最大,整个计算过程中,基本稳定在0.05~0.06之间。在计算过程后期,第09节点的空泡份额在0.03左右。其他所选择的节点的空泡份额基本很低。进而说明在第18和第09节点处的换热过程比较剧烈,结合模型的几何,压力容器的热量导出集中在下封头上部接近过渡段位置和中间位置。
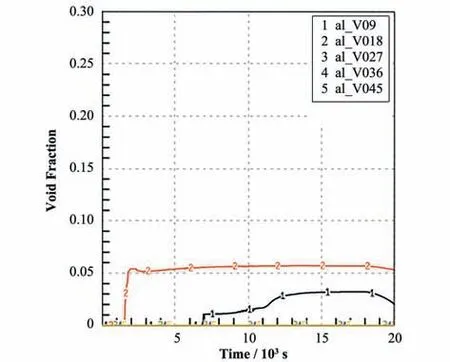
图5 选择节点的空泡份额Fig.5 The void fraction of selected nodes
从各节点流体的温度可见,10 000 s时形成稳定的热量导出,如图6所示,第27、36、45节点的温度基本一致,都维持在330~340 K。从计算结果来看,从第25节点后温度变化不明显,维持在330~340 K。

图6 选择节点的流体温度Fig.6 The fluid temperature of the selected nodes
2.2 下封头外壁面传热分析
选取典型事故序列衰变功率平均值的上限21 MW作为计算的衰变功率,计算比较导出热量和衰变产生热量之间的关系。如图7所示,图中线1为导出热量,线2为衰变热量,在计算10 000 s时,热量导出和衰变功率基本持平,形成有效的热量导出。
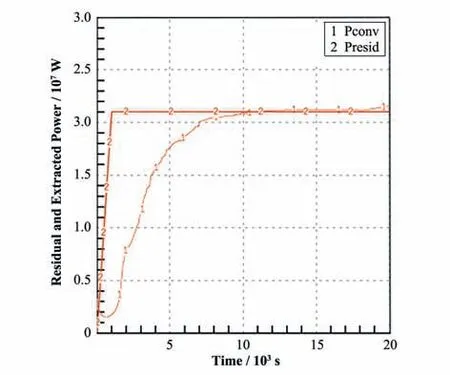
图7 下封头内衰变热量和导出热量Fig.7 The decay heat and heat transfer in the lower head
在下封头外壁面导热过程中,CHF值随下封头表面对应角度变化而变化[16-18],如图8所示,20 000 s时的CHF和壁面导热量,其中1为CHF曲线,CHF值随着角度单调递增,导热量2和3在稳定状态下重合。基本处于金属层和氧化层交界处。图8中线1是由ASTEC程序中内置关系式计算的CHF曲线[19],线2是壁面导出热量,线3是熔融物导入下封头热量。在表面角度为70°~75°位置有显著上升,在此计算中,这个表面角度是熔融物分层的位置,上部金属层侵蚀了一部分下封头厚度导致该角度下封头本体变薄,另外金属层传热流密度较高,因此出现热流密度明显升高的现象。
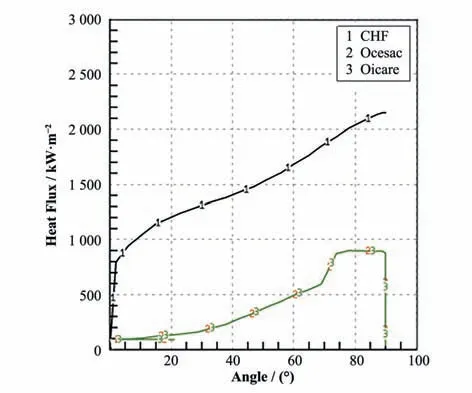
图8 壁面导热量和CHF对比曲线Fig.8 Comparison curve of the surface thermal conductivity and CHF
2.3 下封头壁厚分析
下封头径向方向由内向外划分10个节点。如图9所示,20 000 s时下封头径向方向上节点每一层的轴向温度分布,其中在高度为1.7~2.5 m之间除第10层外,其余各层几乎重合,从而反映了这些压力容器壁面被熔融物熔化,而1.7~2.5 m对应的为金属层所在位置,即压力容器壁面被熔融物金属层熔化。图10为下封头轴向方向各节点的厚度变化,在1.76~2.53 m处下封头的厚度最小,约为0.018 m。
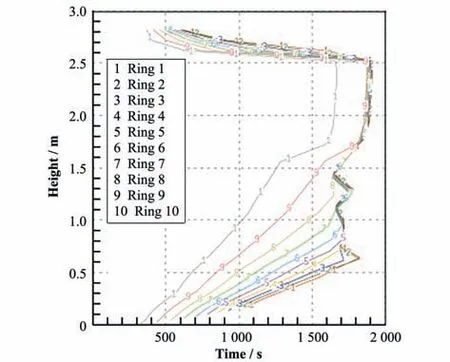
图9 下封头节点沿轴向温度分布Fig.9 The temperature distribution of nodes in lower head along Y axis
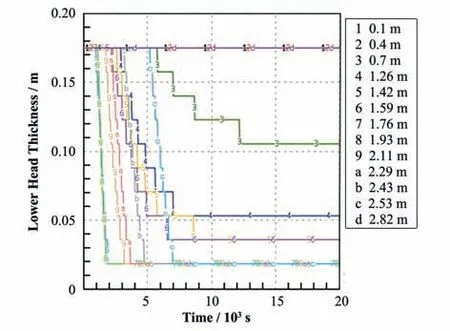
图10 下封头轴向方向厚度分布Fig.10 The thickness distribution of lower head along Y axis
3 结语
针对压水堆的IVR系统,压力容器外部注水冷却下封头外壁面,在衰变功率为21 MW,堆芯熔融物分为两层的情况下,氧化层/第一层熔池厚度平均在1.6 m,金属层/第二层熔池厚度平均在0.8 m。IVR流道中,从下封头下部到上部,冷却液体的流速降低,在较上部位置的区域内,换热较为剧烈,其中CHF最大值处于金属层和氧化层交界处,对应的表面角度为77.5°~80°位置。计算稳定后压力容器下封头剩余壁厚最小处出现在金属层位置,压力容器壁面被熔融物金属层熔化,最终剩余厚度小于
2.0 cm。
作者贡献声明左嘉旭:建模计算及结果分析,起草文章,对文章作批评性审阅;宋维:建模计算及结果分析,文章修改,研究经费支持;安婕铷:建模计算及结果分析,数据处理;庄少欣:建模计算及结果分析,数据处理;石兴伟:论文整体设计,建模计算及结果分析,对文章作批评性审阅。

