考虑负荷季节特性的电价型需求响应最优定价策略

高原，杨贺钧，郭凯军，马英浩

(1.新能源利用与节能安徽省重点实验室(合肥工业大学)，合肥市 230009；2.国网安徽省电力有限公司阜阳供电公司，安徽省阜阳市 236018)

0 引 言

分时电价策略是电力需求侧响应策略的一种，同时也属于电价型需求侧响应范畴。实施分时电价策略可以有效减少负荷曲线的峰谷差，提高电力系统运行的稳定性，同时能有效减少电力系统容量和设备的备用，进而节约电力设备投资成本，改善电力设备利用率。因此，分时电价策略被广泛应用于电力辅助服务市场[1-3]。分时电价策略主要涉及典型日负荷曲线的选取、时段划分和分时电价优化，合理地选取典型日负荷能够有效模拟用户的用电特点，为后续的时段划分以及分时电价优化提供理论支撑，而时段划分作为分时电价优化的先决条件，两者均能对负荷曲线的“削峰填谷”效果产生重要影响。然而，不同季节的负荷曲线具有明显的季节差异性，负荷序列的季节差异性将对峰谷分时电价策略的制定产生影响，因而本文开展时段划分优化模型研究以及考虑负荷季节特性的电价型需求响应最优定价策略研究。

典型日的负荷曲线可以有效代表在研究的时间跨度内样本集的负荷曲线特征，因此，合理地选择典型日负荷曲线是需求响应决策的基础。目前多数研究直接给出某一日的负荷曲线作为典型负荷曲线，无法代表在研究的时间跨度内的全部负荷[4-5]。k均值聚类算法属于无监督聚类算法，简单易实现，且收敛速度快，在聚类领域内应用广泛，因此，本文采用k均值聚类方法对各季节负荷曲线进行聚类分析，获取代表各季节的典型日负荷曲线。峰谷时段划分以获取的典型日负荷为基础从而作为峰谷分时电价优化的先决条件。文献[6]采用模糊C均值聚类算法对峰谷时段进行划分，但存在对初始聚类中心敏感，容易陷入局部最优等问题。文献[7]采用k均值聚类算法进行时段划分，但初始值的随机选择性会导致聚类结果不稳定。文献[8]提出了基于移动边界技术的时段划分模型，采用全枚举峰平谷时段的方式并采用最小化均方距离作为目标函数，虽然克服了聚类结果的不稳定性，但时段划分结果无法有效地反映各个时段间的类间距离与类内距离且时段划分效率较低。因此，本文提出一种基于改进移动边界技术的峰谷时段划分模型，引入峰平谷最小时段划分约束因子以提升时段划分效率，并采用最小化戴维森堡丁指数(Davies-Bouldin index, DBI)[9]作为目标函数，充分考虑不同峰谷时段划分间的类间和类内距离以提升时段划分精度。

不同季节负荷曲线的峰谷特征及负荷水平具有显著差异，而负荷序列的峰谷特征以及大小的不同会对分时电价的设计产生直接影响。文献[10]直接以给定的夏季典型日负荷曲线，提出计及用户需求响应的价格型需求响应策略；文献[11]以夏季某高峰日的负荷曲线作为典型日负荷曲线，讨论了基于用户响应的分时电价时段划分模型；文献[12]选取某月的一天作为典型日负荷曲线，采用等步长迭代技术对其进行峰谷时段划分，在时段划分的基础上采用粒子群优化(particle swarm optimization, PSO)算法对峰谷分时电价进行优化，并讨论了分时电价与电力系统充裕性指标之间的关系。然而，上述文献均直接给出典型日的负荷曲线，没有考虑负荷曲线的不同季节特性，无法获得包含不同季节特性的峰谷分时电价策略。文献[13]建立了考虑负荷季节特性的分时电价优化模型。文献[14]基于各季节负荷曲线聚类结果，建立了在考虑季节特性下的峰谷时段划分修正模型。然而上述文献是通过直接选取或优化获取各季节的典型日负荷曲线，仅能获得各个季节的峰谷分时电价优化结果，无法获得包含不同季节特性峰谷分时电价策略。因此本文将负荷的不同季节特性纳入峰谷分时电价的优化中，建立考虑负荷季节特性的电价型需求响应最优定价策略。

基于上述分析，本文首先给出基于峰谷时段划分和分时电价的电价型需求响应最优决策模型并提出需求响应架构；其次，采用k均值聚类方法来获取各季节的典型日负荷曲线，并提出基于改进移动边界技术的峰谷时段划分模型；然后，建立考虑负荷季节特性的峰谷分时电价优化模型，并采用PSO优化算法求解此模型；最后，采用RTS测试系统负荷序列对所提方法和模型进行验证。

1 电价型需求响应最优决策模型

电价型需求响应决策模型作为一种典型的需求响应决策模型，合理地设计电价型需求响应决策模型可以有效地降低负荷曲线的峰谷差，进而产生诸多收益，如延迟电网投资、降低停电成本和提升电力系统可靠性。本文所研究的电价型需求响应最优决策模型流程如图1所示。

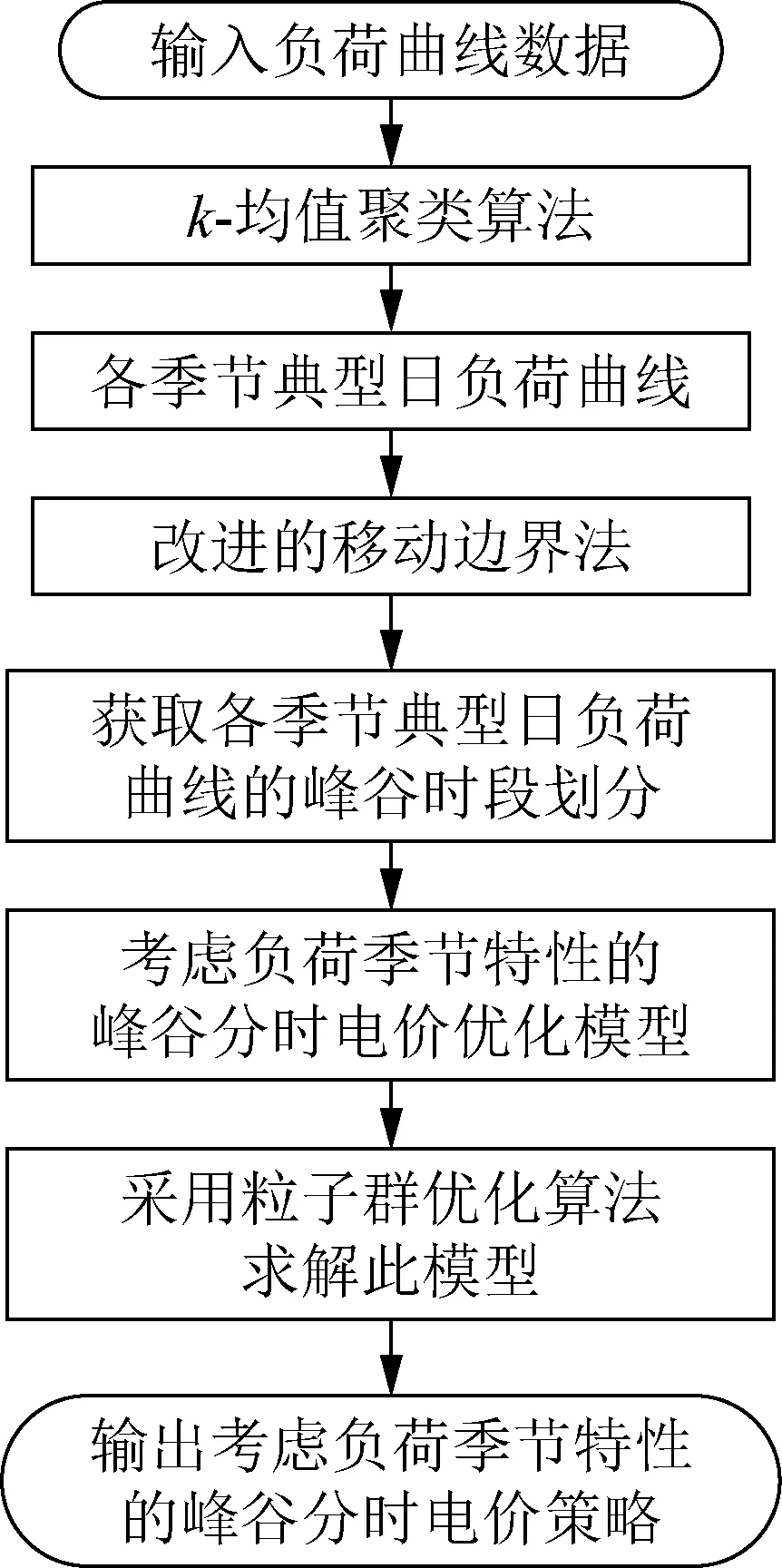
图1 电价型需求响应最优决策模型流程Fig.1 Flow chart of optimal decision model of electricity price demand response

首先，合理地选取典型日负荷曲线及确定峰谷时段划分可以有效地模拟用户在某一时期内的用电特点，为后续的峰谷分时电价优化提供理论支撑，通过负荷曲线聚类算法来获取各季节典型日的负荷曲线；其次，为提升时段划分的效率和精度，提出一种基于改进移动边界技术的峰谷时段划分模型对其进行峰谷时段划分，以获取各季节典型日负荷曲线的峰谷时段划分结果。最后，针对负荷曲线的峰平谷程度具有季节性差异，提出考虑不同负荷季节特性的电价型需求响应最优定价策略，可以根据各季节负荷水平的不同，灵活地选取参与优化的季节数目，获取考虑不同负荷季节特性的峰谷分时电价优化结果。

2 季节典型日负荷曲线选取及峰谷时段划分模型

2.1 典型日负荷曲线的选取

k均值聚类算法根据相似性原则，将各负荷曲线具有相似峰平谷时段的负荷曲线聚为同一类，将峰平谷时段具有较大差异度的负荷曲线划分至不同类。将初始负荷曲线样本记为Z，其中共有n天的负荷曲线数据，即Z={X1,X2,…,Xn}，设每天的负荷曲线聚类维数为m，即Xi={x1,x2,…,xm}。对于给定的负荷曲线样本集，根据负荷曲线之间的距离大小，将负荷曲线样本划分为k个类簇。设给定的负荷曲线样本集划分为C={C1,C2,…,Ck}，则目标函数为各类内的元素与各类内聚类中心的平方和误差E最小：

(1)

式中：μi为类Ci的聚类中心。

(2)

2.2 基于改进移动边界技术的峰谷时段划分模型

针对移动边界技术时段划分效率较低，本文通过添加峰平谷时段约束因子以提升时段划分效率。同时，移动边界技术[8]目标函数采用最小化均方距离，无法有效地刻画峰平谷3个时段的类间与类内距离。本文提出以最小化DBI的值作为目标函数，对负荷曲线进行峰谷时段划分，即最大化不同峰平谷时段划分间的最小距离和最小化各个峰平谷时段内最大距离，通过改变移动变量Vfv,m、Vpf,n的位置来枚举时段划分状态，并以最小化DBI[15]作为目标函数，求解最优峰平谷时段划分模型。

设典型日负荷序列为l={l1,l2,…,l24}，将其从小到大排序得到升序排列的典型日负荷序列l′={l′1,l′2,…,l′24}，设Vfv,m,Vpf,n∈l且Vfv属于谷时段的最大负荷，Vpf属于平时段的最大负荷，本文将移动变量Vfv,m和Vpf,n设置成决策变量，设置时段划分约束因子并以最小化DBI的值作为目标函数，通过式(3)和式(4)建立最优峰谷时段划分模型：

(3)

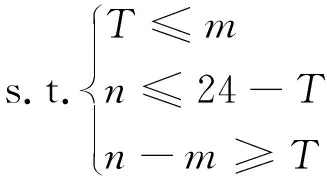
(4)

式中：m、n分别表示升序排列典型日负荷曲线的第m和第n个负荷；T表示在峰谷时段划分中，峰平谷时段负荷的最小个数；k表示聚类个数且k=3；si表示第i个时段负荷点与Ci的标准误差；Dij表示Ci与Cj之间的距离。

(5)

Dij=‖Ci-Cj‖

(6)

(7)

式中：ni表示第i个时段中负荷点的个数；Ci表示同一时段中所有负荷点的平均值。

基于改进移动边界技术的峰谷时段划分优化算法的详细步骤如下：

步骤1：输入时段划分的对象，即典型日负荷序列l={l1,l2,…,l24}。

步骤2：将典型日负荷序列进行升序排列，即l′={l′1,l′2,…,l′24}。

步骤3：初始化决策变量Vfv,m和Vpf,n的值，令m=T、n=2T，其中m∈[T,24-2T]，n∈[2T,24-T]。

步骤4：计算目标函数σDBI(Vfv,m,Vpf,n)的值。

步骤5：更新决策变量Vfv,m和Vpf,n的值。如果n≤24-T，则令n=n+1，否则令m=m+1，n=m+1。

步骤6：终止迭代。如果n=24-T，则终止迭代，否则转到步骤5。

步骤7：输出最小的目标函数DBI的值并输出对应的m、n值。

由上可得到结果，如果l′t∈[l′1,Vfv,m]，则l′t属于谷时段负荷；如果l′t∈[Vfv,m+1,Vpf,n]，则l′t属于平时段负荷；如果l′t∈[Vpf,n+1,l′t]，则l′t属于峰时段负荷。

3 考虑负荷季节特性的峰谷电价优化策略

3.1 考虑季节特性的需求价格弹性矩阵

需求价格弹性矩阵[16-17]能有效地反映需求响应对用户用电行为的影响。而在需求价格弹性矩阵中考虑季节特性可以有效地反映各季节负荷特性的不同，考虑季节特性的需求价格弹性可以表示为：

(8)

式中：s=1、2、3、4分别表示春、夏、秋、冬4个季节；Ep(s)、Ef(s)、Ev(s)分别表示第s个季节分时电价前峰平谷时段的电力需求量；E′p(s)、E′f(s)、E′v(s)分别表示第s个季节分时电价后峰平谷时段的电力需求量；pp(s)、pf(s)、pv(s)分别表示第s个季节的峰平谷电价；p0表示分时电价前的初始电价；χij为电价弹性系数，i=j时为自弹性系数，i≠j为交叉弹性系数。

第s个季节的电价弹性系数具体为：

(9)

(10)

式中：i,j=p, f, v分别代表峰平谷时段。

采用电价弹性矩阵可以求取分时电价之后的电力需求量，根据分时电价前后的电力需求量采用比例分摊技术可以获得第s个季节典型日每小时的负荷：

(11)

式中：t=1,2,…,24表示小时数；Pt(·)和P′t(·)分别表示分时电价前后第t小时的负荷值；p= (pp,pf,pv)代表峰平谷时段电价。

3.2 目标函数

在本文的峰谷分时电价策略的优化过程中，采用最小化负荷曲线的峰谷差和峰负荷[18]，如下所示：

(12)

(13)

式中：Ssum表示参与优化的总季节数。

3.3 约束条件

在考虑负荷季节特性的峰谷分时电价优化中，考虑的约束条件有峰平谷电价约束、用户利益约束、供电公司利益约束、峰谷负荷倒置约束和谷时段最小电价约束，具体如下：

1)峰平谷电价约束。为了防止峰谷电价倒置，设置峰时段电价大于平时段电价，同时平时段电价大于谷时段电价，该约束可以表示为：

C1=pp-pf>0

(14)

C2=pf-pv>0

(15)

2)用户利益约束。实施峰谷电价前后，保证用户的利益不受损失，即实施分时电价后用户所交的电费不高于分时电价前所交的电费，该约束可以表示为：

C3=Qbefore-Qafter≥0

(16)

(17)

式中：Qbefore、Qafter分别表示分时电价前后用户所交的电费。

3)供电公司利益约束。

在保证用户利益不受损的情况下，同时供电公司的利益也不受损，该约束为：

C4=Qafter-(1-δ)Qbefore≥0

(18)

式中：δ表示让利系数[19]。

4)峰谷负荷倒置约束。

为防止优化过程中出现峰谷负荷倒置的情况，设置优化后负荷曲线峰时段负荷最小值大于优化后负荷曲线谷时段负荷最大值，如下所示：

C5=Pp,min-Pv,max≥0

(19)

式中：Pp,min、Pv,max分别表示分时电价后的负荷曲线峰时段负荷最小值和谷时段负荷最大值。

5)谷时段最小电价约束。

由于供电公司发电具有一定的成本，谷时段最小电价不应低于边际电价，即：

C6=pv-pc≥0

(20)

式中：pc为边际成本价格。

3.4 峰谷分时电价优化算法

本文采用权重系数将考虑多重负荷季节特性的多目标优化问题转化为单目标优化问题：

F(p)=αF1(p)+βF2(p)+Y(p)

(21)

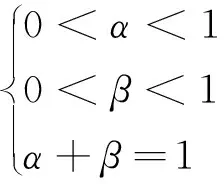
(22)

(23)

式中：α、β为权重系数；Y(p)为罚函数项；Csum表示总约束条件个数；l表示当前迭代到第l次；hi(p)、H[hi(p)]和ζ[hi(p)]如下所示。

hi(p)=max{0, -Ci(p)}

(24)

(25)

(26)

PSO算法具有参数较少、结构简单、可以快速求出问题的最优解等优点[20]，因而在电力系统求最优解问题中广泛应用。本文采用PSO算法来解决上述优化问题，其求解流程如图2所示。

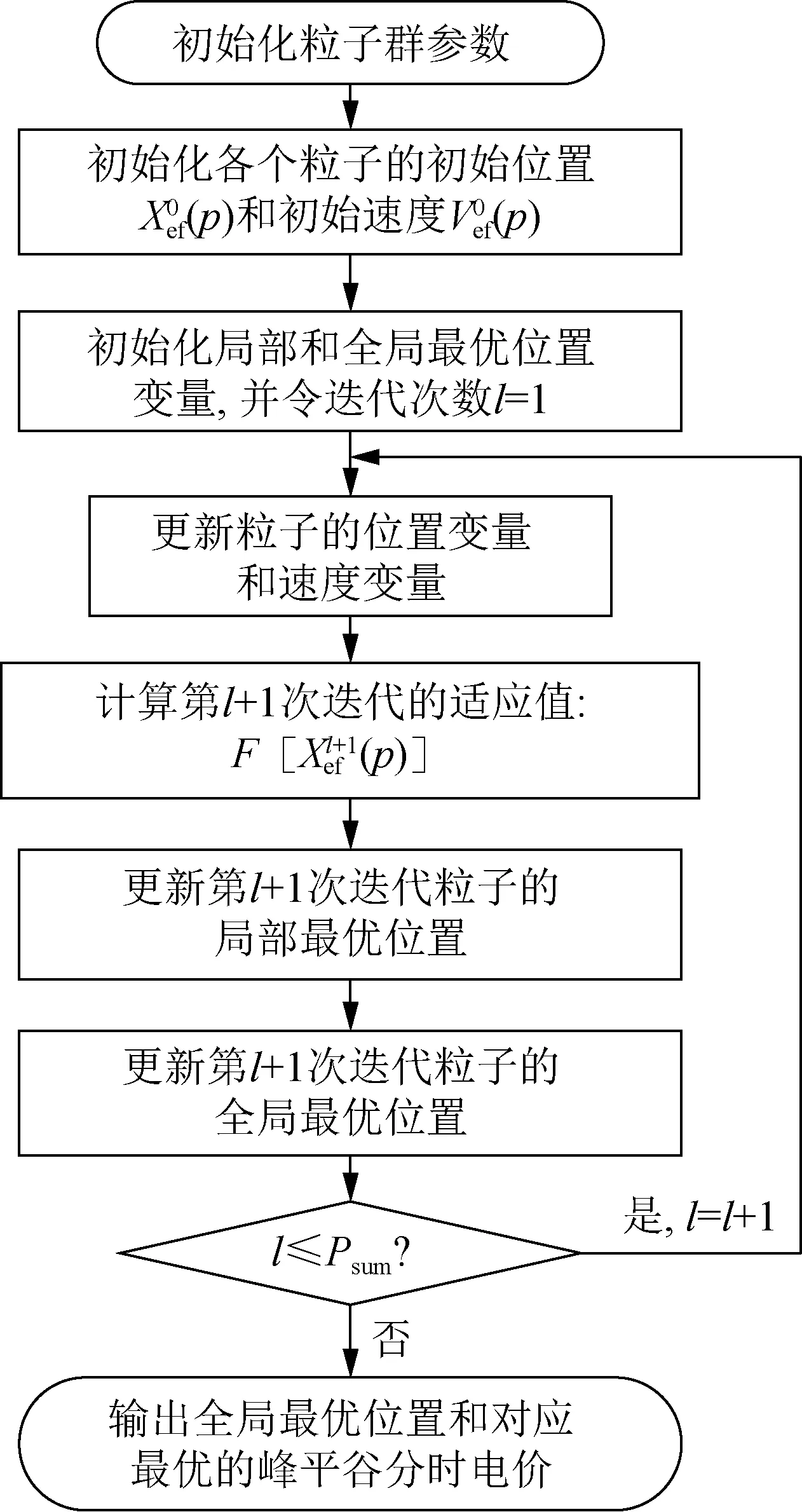
图2 基于粒子群优化算法的峰谷分时电价优化算法流程Fig.2 Flow chart of peak-valley TOU price optimization algorithm based on PSO algorithm

4 算例分析

4.1 基础数据

在本文中，负荷曲线样本集采用RTS[21]提供的时序负荷(标幺值)，春夏秋冬4个季节各91天，共计364天的负荷曲线作为负荷初始聚类样本集。

在峰谷时段分中，峰平谷时段的负荷最小个数为4。本文采用的目标函数权重系数α和β都取值0.5，让利系数δ取值0.062，边际成本价格pc=0.35元/(kW·h)，分时电价之前的初始电价p0=0.65元/(kW·h)。在采用PSO算法求解最优峰谷电价时，设置的峰平谷电价初始值峰时段电价pp=1.00元/(kW·h)，平时段电价pf=0.65元/(kW·h)，谷时段电价pv=0.35元/(kW·h)。本文采用的电价弹性矩阵数据取自文献[22]。

4.2 各季节负荷曲线聚类分析

负荷曲线聚类是获得各季节典型日负荷曲线的基础，同时也是本文在考虑负荷季节特性下进行峰谷分时电价优化的前提。图3给出了不同季节负荷曲线的聚类结果，其中青绿色为各季节原始负荷曲线数据集，蓝色曲线代表各季节负荷曲线聚类结果，从图3可以看出，采用经典k均值聚类算法，可以有效保留各季节原始负荷曲线的典型峰谷特征，进而对各季节典型日负荷曲线进行时段划分和峰谷分时电价优化。

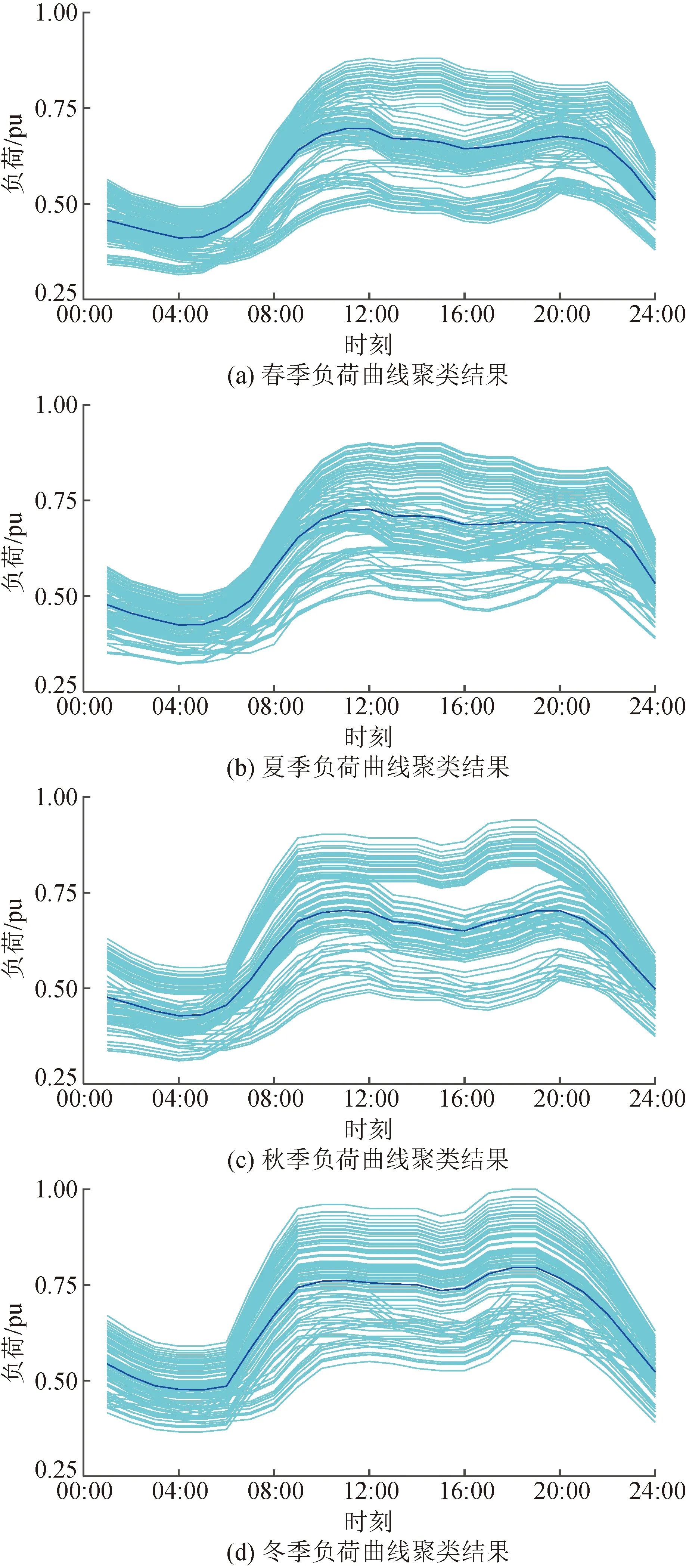
图3 各个季节负荷曲线聚类结果Fig.3 Clustering results of load curves in each season

4.3 基于改进移动边界技术的峰谷时段划分分析

本节采用改进移动边界技术对各季节典型日的负荷曲线进行时段划分，表1给出了采用本文提出方法和移动边界技术得到的DBI值和计算时间。以春季和秋季典型日负荷曲线为例，图4和图5给出了采用本文所提时段划分方法和移动边界技术对春季和秋季典型日负荷曲线进行时段划分的结果。从图中可以看出，由于在枚举时段划分状态的过程中添加了时段划分约束因子，即约束各负荷曲线峰平谷的最小时段数为4，采用本文所提方法可以有效地提升时段划分效率。本文采用最小化DBI的值作为目标函数，即以不同时段划分间的类间距离和类内距离为测度，相对于移动边界技术以最小化均方距离为目标函数，即以峰平谷时段各类内距离为测度，可以有效地提升时段划分精度。

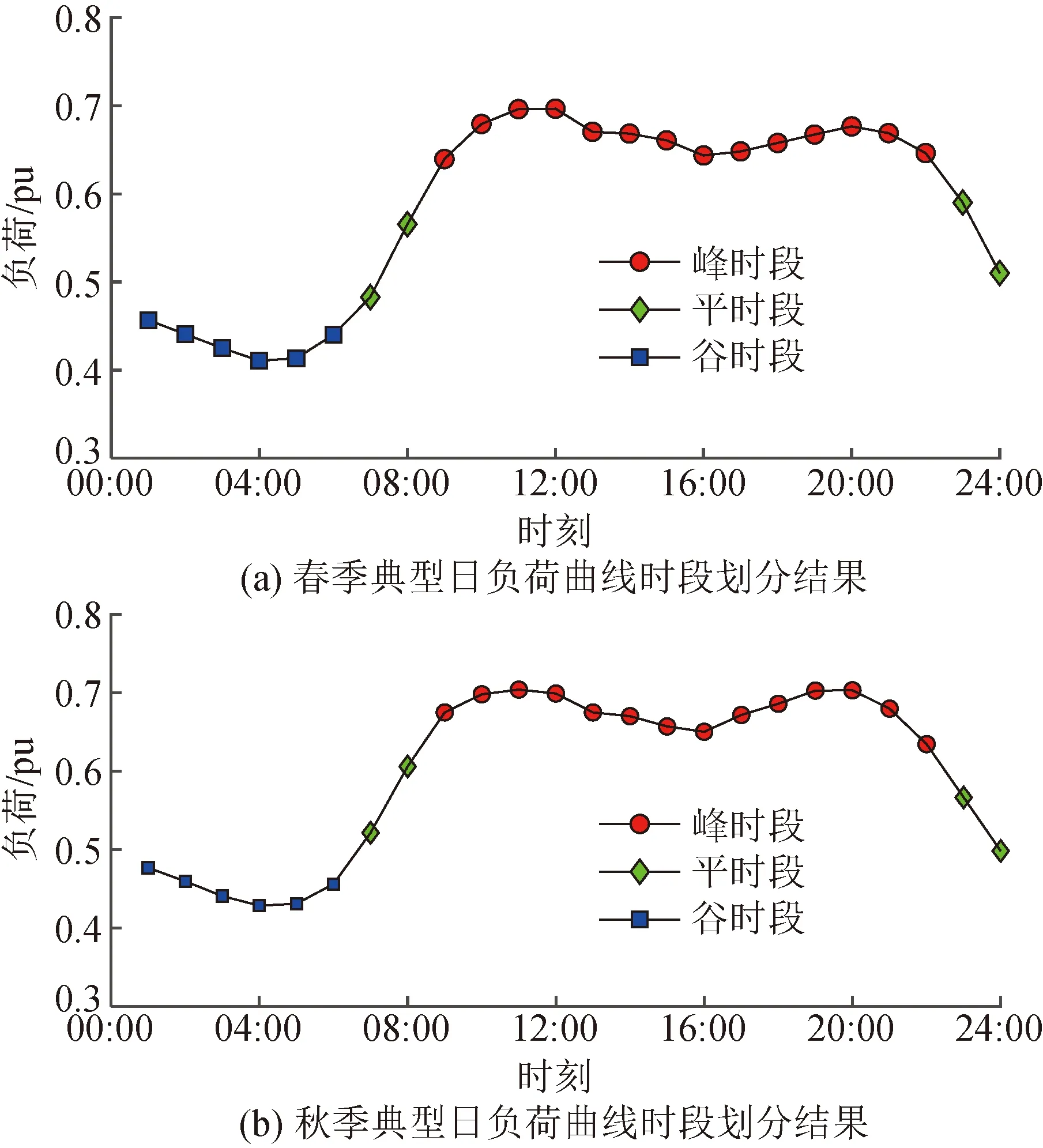
图4 春、秋季节典型日负荷曲线时段划分结果(本文提出方法)Fig.4 Period partitioning results of typical daily load curve in spring and autumn (proposed method)

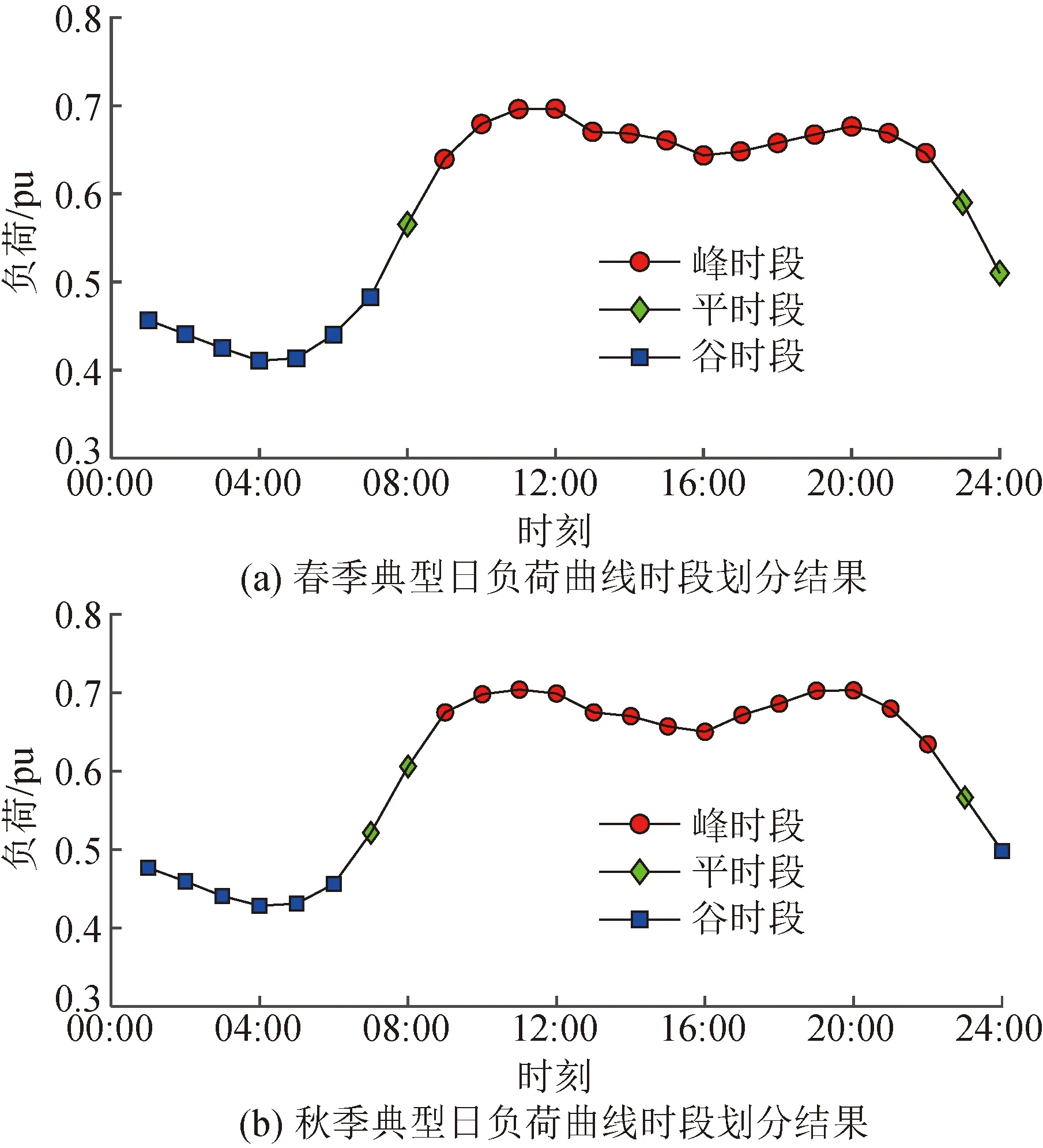
图5 春、秋季节典型日负荷曲线时段划分结果(移动边界技术)Fig.5 Period partitioning results of typical daily load curve in spring and autumn (the moving boundary technology)

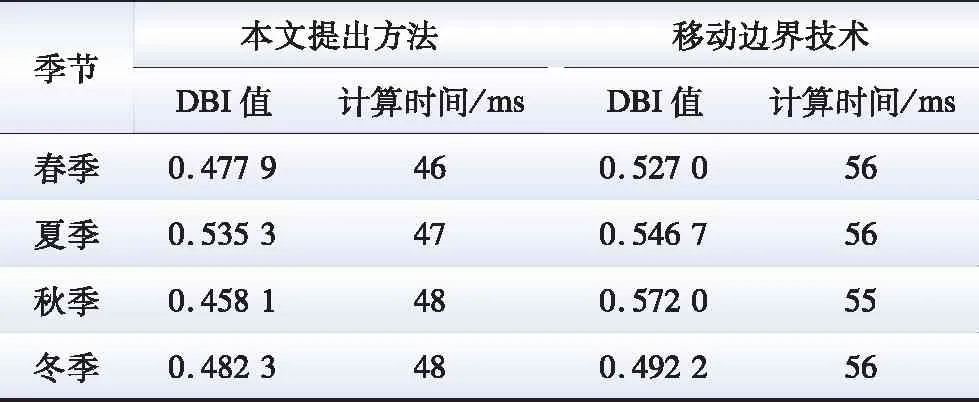
表1 不同时段划分方法分析Table 1 Analysis of results of different period partitioning methods

由上述分析可以看出，本文所提峰谷时段划分方法通过设置时段划分约束因子并以最小化DBI的值作为目标函数可以有效地提升时段划分精度和效率，对于获取一个科学和合理的时段划分结果具有重要意义，同时也为后续的峰谷分时电价优化奠定基础。

4.4 考虑负荷季节特性的峰谷分时电价优化分析

本文在优化峰谷分时电价时考虑负荷的不同季节特性，选取参与优化的总季节数Ssum分别为1、2、3、4作为典型场景来优化负荷曲线。其中Ssum=1表示以春季典型日负荷曲线为代表进行优化，Ssum=2表示以春季和夏季典型日负荷曲线为代表进行优化，Ssum=3表示以春季、夏季和秋季典型日负荷曲线为代表进行优化，Ssum=4表示以春季、夏季、秋季和冬季典型日负荷曲线为代表进行优化。

本文选取粒子数目Psum=200，种群数量为50。以Ssum=1和Ssum=4时为例进行分析，采用粒子群优化算法重复求解10次，适应值随迭代次数的收敛过程如图6所示，从图6可以看出，当Ssum=1时，最差的将在40代左右收敛，最好的在10次左右迭代收敛，当Ssum=4时，最差的将在40代左右收敛，最好的在5次左右迭代收敛，且在2种典型场景下，目标函数的适应值均能达到相同的稳定状态，说明本文采用PSO算法具有较高的求解效率，并且可以得到理想的峰谷分时电价优化结果。

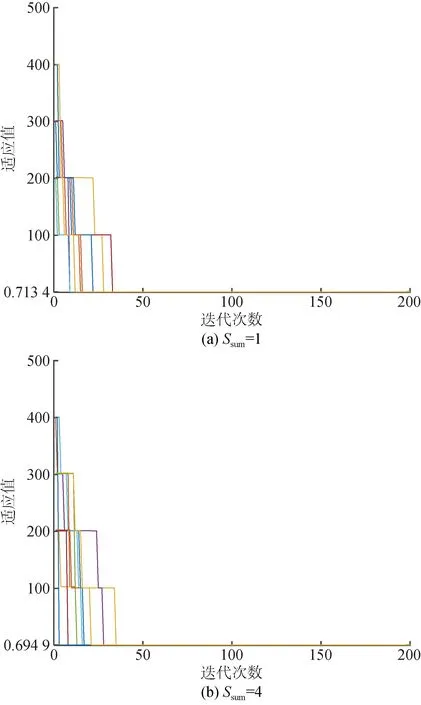
图6 适应值随迭代次数变化的收敛过程Fig.6 Convergence process of fitness changing with the number of iterations

采用PSO算法对本文所提考虑负荷季节特性的峰谷分时电价进行优化，考虑不同负荷季节数目的峰、平、谷分时电价优化结果及与初始电价p0的对比如图7所示。

从图7可以看出，在实施分时电价以后，峰时段电价高于初始电价p0，以期望减少用户在高峰时期的用电量，降低用户在高峰时期的负荷，以实现对负荷曲线“削峰”的目的。谷时段电价低于初始电价p0，且始终处于较低的水平，希望通过设置较低的谷时段电价，增加用户在此时段的用电量，以实现对负荷曲线“填谷”的目的。而平时段电价相对于初始电价变化较小且低于初始电价p0，希望平时段的负荷能吸引少量来自高峰时期的负荷且总体应当保持稳定状态。

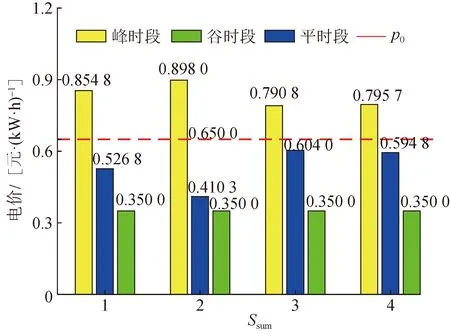
图7 考虑不同负荷季节数优化得到的峰、平、谷时段电价与初始电价对比Fig.7 Comparison of peak, flat and valley electricity prices and initial electricity prices optimized by considering different load seasons

对于优化后的负荷曲线，选取春季典型日负荷曲线为例进行分析，分时电价前后考虑不同负荷季节数优化得到的负荷曲线对比如图8所示。从图8中可以看出，与分时电价之前的负荷曲线相比，由于在供电公司利益约束中设置了让利系数，导致分时电价后的用电量略低于分时电价之前的用电量，而同时由于峰谷分时电价的影响，使分时电价后的峰时段负荷下降，平时段负荷几乎不变，谷时段负荷上升，表明在考虑不同或多种负荷曲线季节特性的情况下，本文所提峰谷分时电价最优定价策略同样可以有效地实现对负荷曲线的削峰填谷。

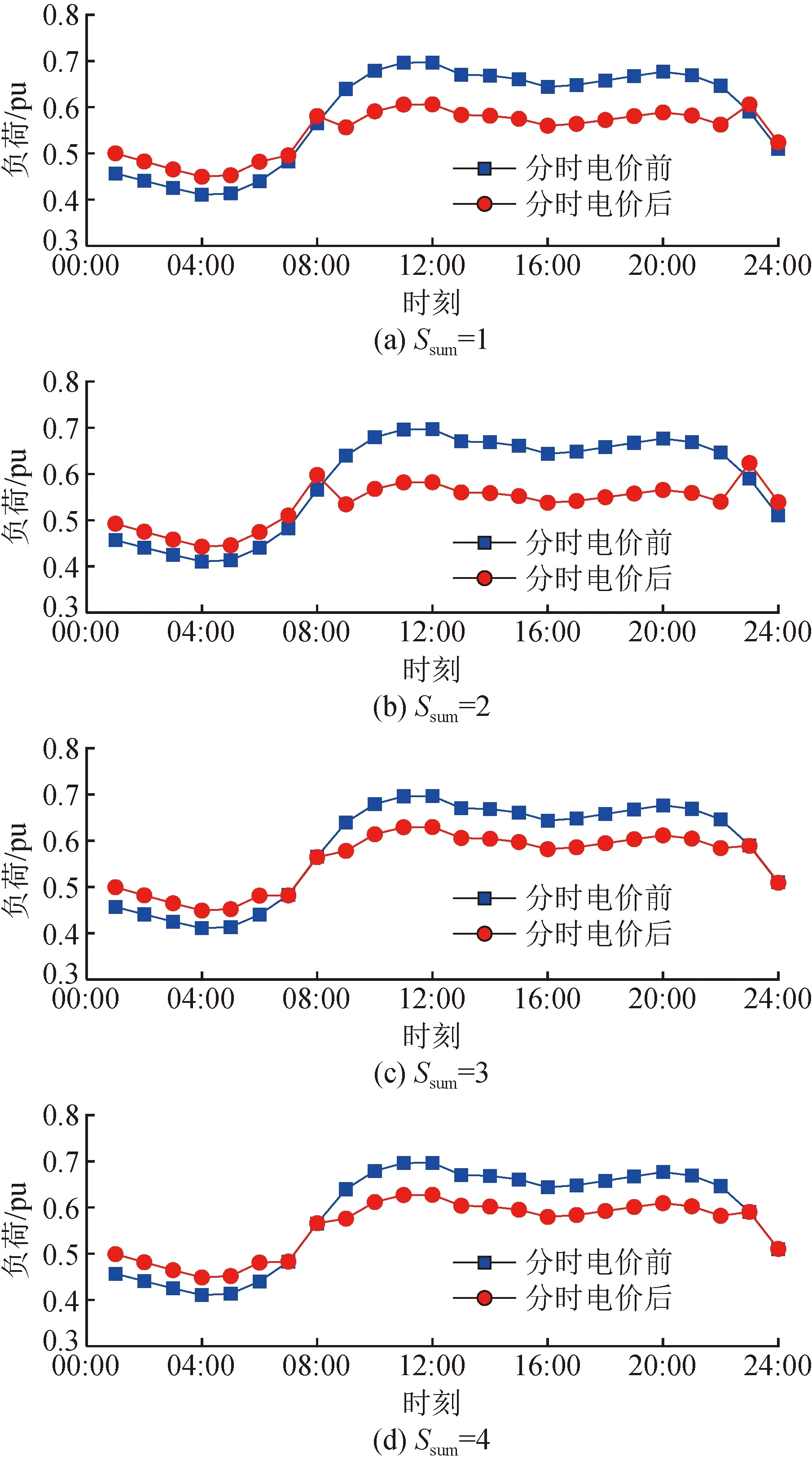
图8 分时电价前后考虑不同负荷季节数优化得到的负荷曲线对比Fig.8 Comparison of load curves obtained by considering the optimization of different load seasons before and after TOU

5 结 论

本文针对不同季节负荷曲线具有明显的差异特性，采用k均值聚类算法获取各季节典型日负荷曲线，并采用改进的移动边界技术对各季节典型日负荷曲线进行时段划分，最后建立峰谷时段划分模型并提出考虑负荷季节特性的峰谷分时电价定价策略，得到相关结论如下：

1)建立了基于改进移动边界技术的峰谷时段划分优化模型。通过设置峰平谷时段划分约束因子，并采用最小化DBI的值作为目标函数，充分考虑不同时段划分情况下的类间和类内距离，可以有效地提升时段划分效率及时段划分精度。

2)提出了考虑不同负荷季节特性的峰谷分时电价最优定价策略。通过采用PSO算法对考虑不同季节特性的负荷曲线进行优化，可以在保留各季节典型日负荷曲线峰谷特征的同时，有效地对负荷曲线进行削峰填谷，得到考虑不同负荷季节特性的电价型需求响应最优定价策略。