基于改进的粒子群优化神经网络算法的海平面变化预测分析

张 宇 贺小星 孙喜文

(1. 江西理工大学 土木与测绘工程学院, 江西 赣州, 341000;2. 东华理工大学 测绘工程学院, 江西 南昌, 330013)

0 引言

导航、海污染扩散建模以及海域能源勘测等工业用途都需要海洋空间域上的精确潮汐预报[1-2]。由于潮高受到海水温度,盐度、陆地水体以及地球物理过程等因素的联合影响,低、高潮位之间并不是总是反相变化,而是正反相交替变化,这也使得一些经典模型在潮位预报中得不到较好的精度。

本文基于分群思想,构建了一种多个分群间协同进化的智能粒子群优化网络模型(swarm strategy particle swarm optimization-back propagation,SSPSO-BP),通过建立多个具有信息交流能力的分群及在粒子进化进程中引入“变异算子”,采取自适应惯性权重调整策略在搜索过程指引粒子走向全局最优解,来实现智能化的参数搜索。针对日本沿岸在PSMSL网站上Oga站的连续月数据,SSPSO-BP模型在潮位预报中与实测值具有高度的一致性,潮位特征的预报准确度较高[3]。

1 BP神经网络与PSO算法介绍

1.1 BP神经网络算法原理

BP神经网络是一种依赖误差反传机制的多层前馈网络。在网络训练过程中,通过误差反传不断调整连接参数,使输出与期望间的均方误差达到目标精度或者迭代次数达到阈值[4-5]。

BP神经网络训练的主要步骤如下。

(1)网络初始化：选定网络的输入层节点数为N,隐含层节点数为H,输出层结点数为M,设定输入层与隐含层、隐含层与输出层神经元之间的连接权值Wij,Wjk及激活函数。

(2)隐含层及输出层计算。

(3)修正连接权值。

(4)判断全局误差或学习次数是否满足要求,若满足则训练结束,否则继续选取样本输入及期望输出,返回到步骤(2)继续对网络进行训练,直至达标。

1.2 标准PSO算法

实际工程问题的解经过编码后可以看成一个在D维搜索空间的粒子[6]。粒子在搜索域中的速度和位置的更新公式为

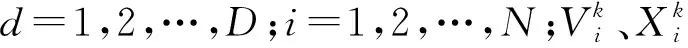
由式(1)、式(2)可知,w越小,粒子飞行时的迭代步长越小,越趋向细致的局域搜索;w越大,粒子飞行时的步长越大,粒子越趋向于宽泛的全局搜索。常见的惯性权值调整策略为

式中,t为当前迭代数;tmax为最大进化次数。

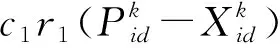
1.3 基于分群策略的粒子群改进算法

基于分群策略的粒子群改进(particle swarm algorithm based on swarm strategy,SSPSO)算法(图1)将粒子分为基础群Q1、Q2、综合群Q3三个群体,分群间在同一搜索空间中飞行找寻最优位置,且在搜索过程中保持种群之间的信息交流。同时在粒子进化的过程中保留其自身的思维,使得其能够依据隔代适应度差异自适应调整惯性权重以及根据进化程度改变学习因子来完成在整个过程中智能调整搜索策略,并且引入变异算子在粒子基本丧失进化能力时进行变异,保持粒子群的种群多样性,走向智能化的方向[10-11]。

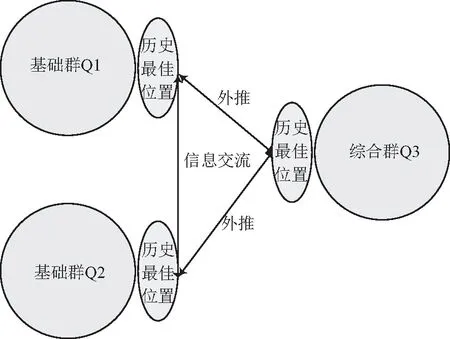
图1 分群策略示意图

综合群S3的进化方程：

(6)

(7)

式中,m1、m2分别为基础群Q1、Q2粒子的适应度,决定了基础群的粒子速度对综合群速度的影响大小。基础群Q1、Q2进化方程和标准粒子群进化式(1)、式(2)相同。综合群Q3进化的过程的顾及了基础群Q1、Q2速度的影响,并保证了适应值高的群体对综合群有着更大的影响,上述进化模式,利用了所有的分群信息,既保证了群体间的联又提高了种群的多样性。

实际搜索过程中粒子轨迹呈现复杂的动态变化,LDI-PSO调整策略(式3)并不能反映实际的搜索过程,并且惯性权重下降的最优斜率受各种因素的影响,常数的变化斜率并不适用于所有的优化问题[12-13]。因此当惯性权重w较小,且fitk与fitk-1的差值小于一个极小的固定值ε时,则说明此时粒子大量聚集,此时采用w=w+rand·w调节惯性权重使其变大,增强粒子的全局搜索能力,使粒子摆脱局部极值。同理惯性权重w较大则表明粒子间的搜索经验分享不足,此时采用w=w-rand·w减小惯性权重,加强粒子间的信息交流。惯性权重w调整公式为

(8)

整个搜索进程中,当粒子适应度的隔代差值为一个极小数并且以一定距离偏离全局最优,可认为粒子陷入局部最优值,丧失了向全局搜索的能力。为了让粒子保持向其他区域搜索的活力,使种群避免出现过早聚集的情况,SSPSO算法引入变异算子防止种群出现“早熟”。我们用种群适应度方差σ2来描述种群聚集度,σ2定义为

(9)

式中,fitavg为种群适应度平均值;f为归一化因子，f=max{1,|fi-favg|}

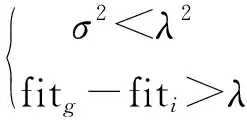
式中,λ为收敛精度,根据实际问题设定。满足上述条件的粒子速度降为0,丧失向其他区域搜索的能力,此时引入变异算子,粒子的速度更新公式变为

(10)

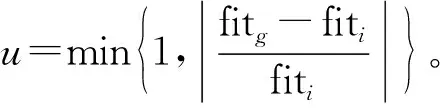
2 基于SSPSO算法的BP神经网络模型

基于SSPSO优化的BP网络模型的实现包含如下基本步骤：确定网络的结构、初始化基础群和综合群、计算分群粒子的适应度、依据一定策略更新速度及位置[14-15]。算法实现的流程如图2所示。

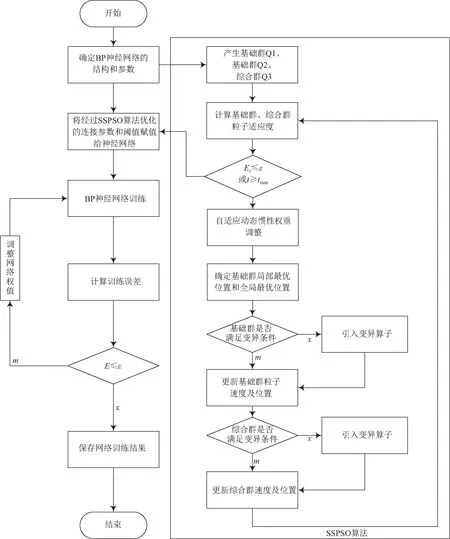
图2 SSPSO算法优化BP神经网络实现流程

3 应用实例及结果分析

本文使用的验潮站数据由PSMSL网站提供,PSMSL成立与1933年,位于利物浦的国家海洋中心,负责全球验潮站海平面数据的收集、发布、分析及解释。PSMSL网站发布的资料为RLR格式的数据,RLR版本的验潮数据分为月平均数据和年平均数据。日本沿岸在PSMSL网站(https://www.psmsl.org/)上约有35个验潮站,本文利用Oga站2000—2012年的连续月数据进行潮位特征预报。

3.1 SSPSO-BP算法的实现以及结果分析

本文选择200期的连续月观测数据代入SSPSO-BP模型中,图3为两种模型性能对比。

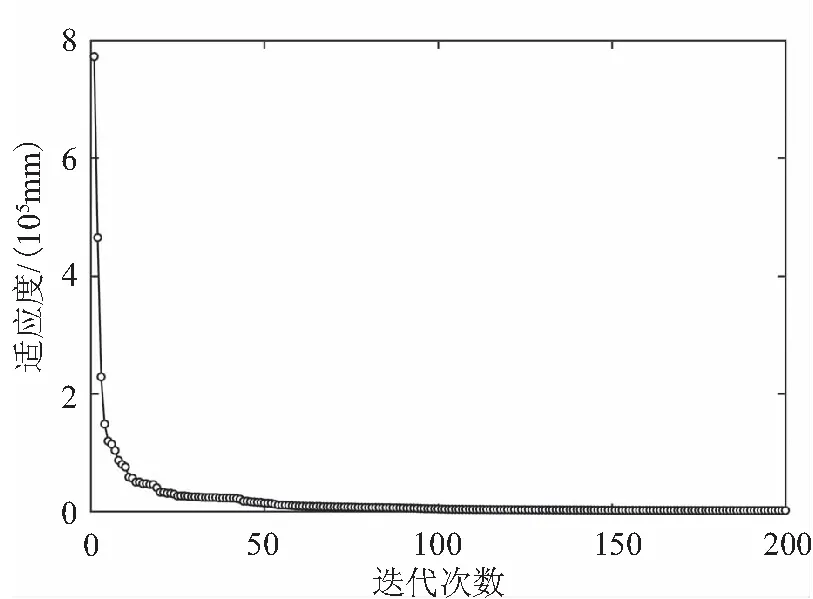
(a)PSO误差曲线

由表1可知,PSO-BP、SSPSO-BP网络比标准的BP神经网络收敛次数明显减少,引进粒子群算法大大减少了神经网络的训练时间。由图4可以看出,综合群粒子在进化过程中会依据自身的搜索状态自适应地动态调整惯性权重以改变搜索策略,增加全局搜索能力,在第376次进化时综合群中出现粒子聚集现象,群速度降为0,此时惯性权重发生跳变,帮助粒子群继续向其他区域搜索。另外SSPSO算法引入了变异算子,理论上算法的迭代次数应该增加,但是实际上分群思想保证了粒子种群的多样性,寻找最优解的能力明显得到提高,从表中看出,SSPSO-BP模型无论是训练时间还是均方误差都相较于PSO-BP模型有所提高。

表1 训练结果对照

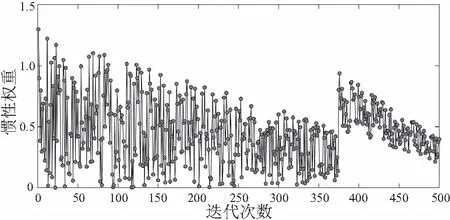
图4 自适应动态调整惯性权重

3.2 验潮站潮位预报

以日本沿岸的Oga站为例分析比较后100期潮高预报值与实测值,图5为Oga站逐月潮位资料。

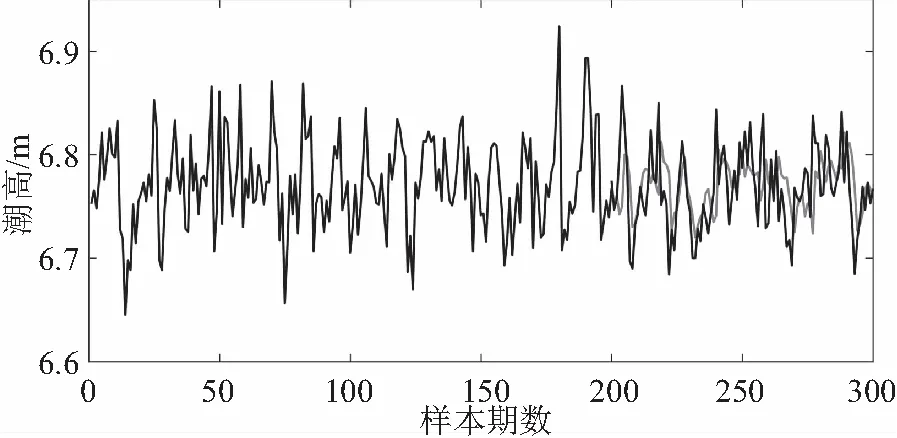
图5 潮位趋势预测

海域潮高变化既是海域潮汐性质的体现,也是潮波系统间的作用过程和机制的反映。从图5可以看出,Oga站上低潮位、高潮位间的关系较为复杂,它们两者并不是严格反相变化,而是呈现正反相交替的变化趋势。SSPSO模型在采样频率小的潮位资料上可以很好地复现潮位变化趋势,并且高潮位和低潮位时刻基本一致。

利用Oga站2000—2012年里的连续月潮位资料对完成训练的三种模型进行仿真,并将仿真结果和实测潮高进行对比。对比结果见图6,两种模型的性能指标对比结果如表2所示。

图6可以看出2000—2012年Oga站的潮高长时间处于高潮位,在2010年9月出现了低于平均海水面的低潮位时刻。SSPSO模型在低频潮位资料上,预测值与实测值的一致性较好,高潮位与低潮位时刻基本对应,高潮时刻最大潮高差为7.37 cm,低潮时刻最大潮高差为4.21 cm,相比标准BP神经网络及PSO优化神经网络最大潮高误差大大减小。另外,SSPSO-BP模型的平均绝对误差、均方误差相较于BP神经网络分别提升了16.2%、79.2%,相较于PSO-BP神经网络提升了13.9%、79.6%,可以看出SSPSO-BP神经网络模型对于潮位预报的准确度和精度都有了较大的提升。

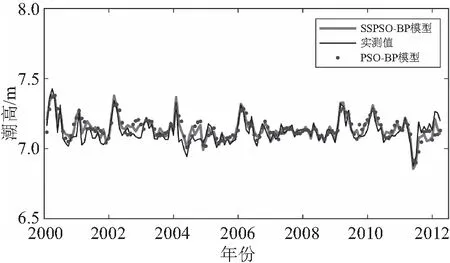
图6 模型预测曲线对比

表2 三种模型潮高预测误差对比

4 结束语

SSPSP算法与BP神经网络结合对BP网络的初始权值和阈值进行优化选择,将综合群的最佳位置作为BP神经网络参数初值并且通过不断的学习进行反向调整,最终产生一个经二次优化的参数向量。由于SSPSO算法进行了BP神经网络的初次寻优,大大减少了BP神经网络的迭代次数,在潮位预报中能够很好地预测潮位特征。

(1)基于分群策略的粒子群优化网络通过分群之间的信息交换以及进化进程中的变异,更加有利于找到全局最优解,相比于传统模型大大减小了陷入局部极值的概率。在低频潮位资料的背景下,也能很好地复现海平面变化趋势,保证高低潮位时刻的一致性。

(2)SSPSO-BP神经网络模型有效地回避了海域潮汐以及多潮波系统作用等复杂因素的影响,采用线性逼近的思想来模拟多因子的作用机制,在高低潮位的振幅以及对应时刻上保持良好的一致性,在潮高差、潮时差等潮位特征上也有很好的预报效果。