基于改进自抗扰的变流系统直流母线电压波动抑制策略

周雪松，郭帅朝，马幼捷，李月超，马 闯

基于改进自抗扰的变流系统直流母线电压波动抑制策略

周雪松，郭帅朝，马幼捷，李月超，马 闯

(天津理工大学电气工程与自动化学院，天津 300384)

在直流母线电压波动的情形下，光伏并网变流系统易出现输入输出侧功率传输不平衡、运行不稳等问题，因此提出一种改进线性自抗扰控制策略。首先，建立变流系统物理模型和数学模型，并分析能量传输不平衡原理。然后，设计一阶线性自抗扰控制器取代传统比例积分矢量控制器。进一步，为加强扩张观测器扰动观测能力，引入新型参数解耦方法，形成解耦型改进自抗扰控制，提高系统的快速性和抗扰性。最后，依托频率响应特性曲线和多种模拟工况进行仿真验证。结果表明：相较于传统控制策略，改进线性自抗扰既具备优越的抑制直流侧母线电压波动的能力，又具有良好的扰动抵抗能力与短时暂态故障穿越能力，保证了系统的功率传输平衡与正常平稳运行。

改进自抗扰；直流母线电压；观测器；比例积分控制；参数解耦

0 引言

在能源危机的背景下，以总书记提出的双碳目标“碳达峰，碳中和”为牵引，以“绿水青山就是金山银山”为口号，寻找具有绿色、环保、无污染等特性的可再生能源来减缓环境恶化的趋势[1]。光伏系统的建立与应用为改善能源消耗和环境污染奠定了必要的基础。作为光伏系统输入与输出侧能量流动的中间桥梁，变流器在电力系统中扮演着不可替代的角色[2]。作为变流器的输入侧部件，直流母线电容的电压波动将造成功率滞留问题，同时会引起变流器输出侧的能量利用率降低，对系统的经济性构成一定的威胁[3]。为保证直流母线电压的平稳和变流器高能量输出，必须对系统施加一定的控制策略。

比例积分控制作为传统矢量控制的代表，具有深远的应用历史[4]。但对于多变量，强耦合的复杂系统由于耦合回路的存在，比例积分控制将使系统的接线复杂程度加大，可靠性大大减弱，系统的故障穿越能力和扰动抵抗能力大大降低，对抑制直流母线电压波动存在一定的缺陷。作为新型控制手段的代表，自抗扰(linear active disturbance rejection control, LADRC)是在大量数学推导与物理实验的基础上形成的一种先进控制器。为降低非线性自抗扰的调参难度，提出了线性自抗扰控制(linear active disturbance rejection control, LADRC)，降低了参数调节的难度。目前，自抗扰在电动汽车、军工控制等领域得到了广泛的应用，成为了继比例积分控制后的典型代表。为使自抗扰下的并网变流系统控制效果更佳，文献[5-6]在LADRC的基础上引入非线性环节，但控制器数学模型的表达形式较为复杂，调节参数较多，与工程实际中的近似处理和简化应用存在一定的隔阂。文献[7]在原有控制器的基础上，加入基于输出信号误差的微分项信号，提高了系统的收敛可靠性，但新加入的微分项使调节参数增多，加剧了系统的参数调节难度。文献[8-9]对线性扩张观测器做升阶处理，但高阶观测器数学模型较为复杂，且升阶后的观测器参数调节难度更大，加重了工程技术人员实际的应用负担。文献[10]引入滑模控制，虽达到了对直流母线电压波动的良好控制，但滑模的抖振现象难以完全克服。文献[11-12]引入模糊理论形成模糊自抗扰，模糊自抗扰结合当下人工智能和控制，但响应速度慢，难以满足系统快速性的要求。

本文从自抗扰控制出发，以抑制变流器直流母线电压波动为目的，对LESO做重新接线处理，达到参数解耦目的，形成改进LADRC。对并网系统进行仿真，验证了改进LADRC控制下的系统既可以抑制母线电压波动，又具备了抗扰性和快速性的优良潜能。

1 变流器数学模型建立及能量分析

1.1 变流器数学模型建立

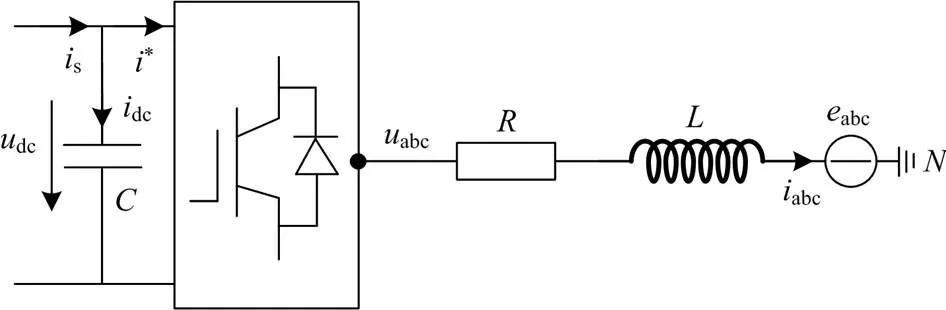
图1 三相变流器拓扑图

根据图1可建立三相变流器在abc静止坐标系下的数学模型。对于控制器而言，若输入为交流量，则达不到理想的控制效果。因此，利用Park变换，建立三相变流器在旋转坐标系下的数学模型，如式(1)所示。

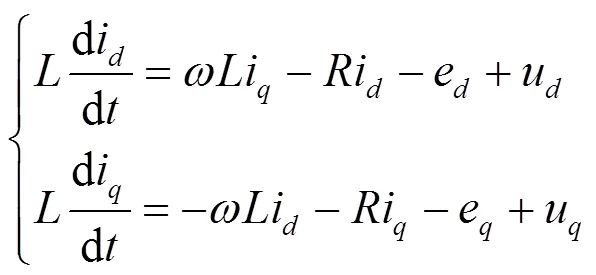
以直流母线电压为状态变量，根据小信号理论，建立直流母线侧的数学模型如式(2)所示。

1.2 能量分析

直流母线电容作为直流与交流的中间环节，其流过的瞬时功率如式(3)所示。

2 一阶改进线性自抗扰设计

2.1 传统LADRC设计

线性自抗扰是在非线性的基础上，经线性化得到。线性自抗扰包括线性扩张状态观测器(linear extend state observer, LESO)与线性状态误差反馈控制律(linear state error feedback, LSEF)。LADRC下的多变量、强耦合系统可实现自然解耦，规避了解耦回路的设计，提高了系统的可靠性和抗扰性。

由式(2)可知，系统的数学模型为一阶微分方程，应设计一阶线性自抗扰控制器对其进行控制。为简化分析，做出如式(4)所示的定义。

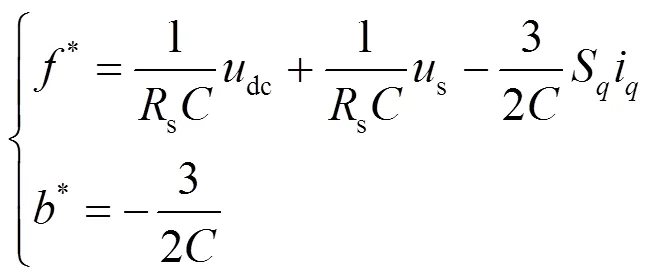
可将式(4)改写为式(5)。

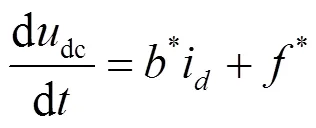
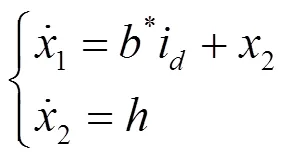
2.2 LESO设计

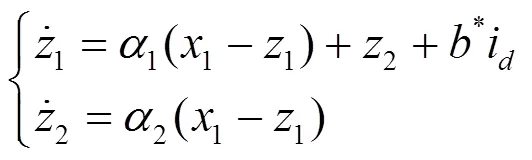
2.3 LSEF设计

对比传统比例积分矢量控制，LADRC的最大优势在于不需事先了解被控对象的数学模型以及外扰和内扰表达形式。对于一阶系统而言，其最终将被表示为单积分器系统。为了转成单积分器的形式，设计LSEF如式(9)所示。

传递函数作为输入和输出关系的直接表达，它的表达形式可反映多方面的内容。基于上述对一阶LADRC的设计，可写出系统输出变量关于扰动变量的传递函数，如式(11)所示。

2.4 改进LADRC设计

引入微分信号对LESO的数学模型进行重组，即对式(11)进行改造，经改进后的数学模型如式(12)所示。

依据式(9)和式(12)可写出经改进后的扰动传递函数，如式(13)所示。

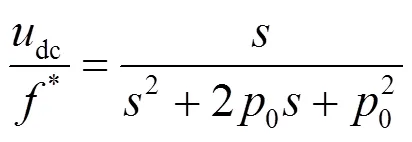
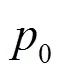
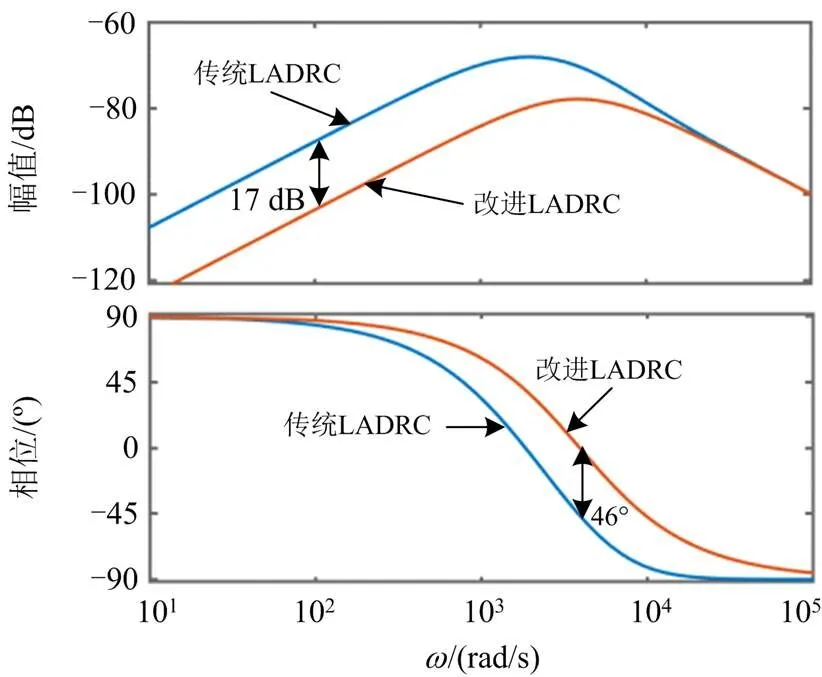
图2 传统型与改进型频率特性对比图

基于式(9)和式(12)，可建立电压外环改进自抗扰结构图，如图3所示。

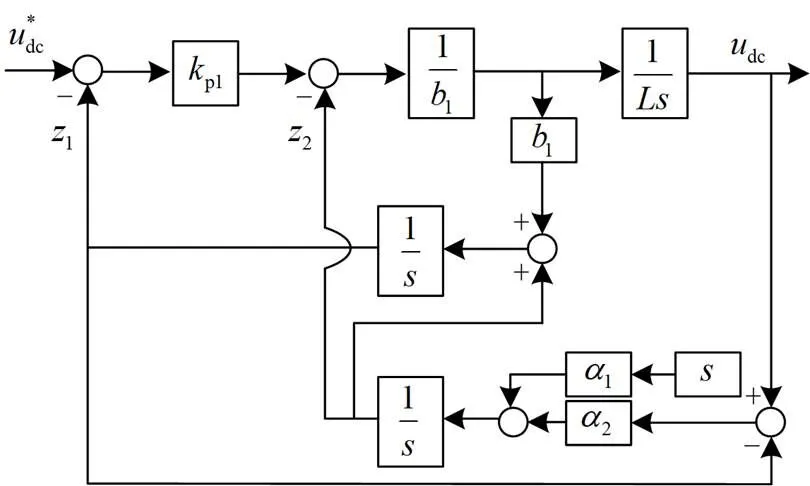
图3 电压外环改进自抗扰结构图

3 电流内环一阶改进自抗扰及串级控制设计

3.1 电流内环一阶改进自抗扰设计

变流器的数学模型在轴和轴存在耦合，传统矢量控制需引入对侧电流进行解耦处理，增加硬件成本的同时，加重了系统收敛的负担。为规避解耦回路的设计，建立一阶改进自抗扰。

将式(1)转为式(14)。

根据电压外环所设计的一阶改进自抗扰控制，建立电流内环的改进自抗扰控制，其LESO的数学模型如式(16)所示。

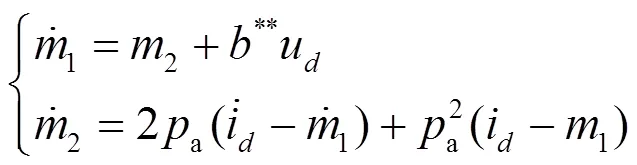
为使系统转变为积分串联型系统，对电压外环进行扰动补偿，LSEF的数学模型如式(17)所示。

由式(16)和式(17)可建立电流内环改进自抗扰结构图，如图4所示。

图4 电流内环改进自抗扰结构图

3.2 串级改进自抗扰双环控制策略

基于上述对一阶改进自抗扰控制策略的设计，建立以电压和电流为控制量的双闭环结构图，如图5所示。图中：LESO1为电压外环的观测器，LESO2为电流内环的观测器，LSEF1为电压外环的控制器，LSEF2为电流内环的控制器，object1和object2分别为内环和外环的被控对象。

图5 双闭环结构图

为方便求解闭环系统的传递函数，将图5等效为含扰动项的双闭环结构图，如图6所示。

图6 含扰动项的双闭环结构图

由式(9)、式(12)、式(16)和式(17)可建立双闭环系统的传递函数，如式(18)所示。

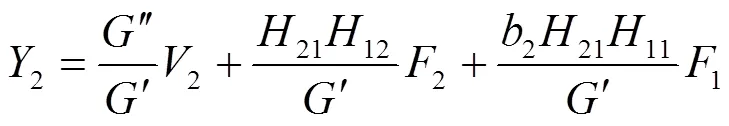
由图7可得到串级改进自抗扰下的三相变流器闭环传递函数，如式(20)所示。

图7 含被控对象的双闭环结构图

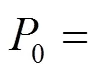
由图8(a)可知，在幅频特性曲线中，低频段和高频段两种控制策略处于重合状态，具有相同的时域性能，但在中频段103rad/s处，传统LADRC出现了明显的谐振尖峰，幅值增量约为3 dB，根据谐振峰值与阻尼比成反比的数学特性，此谐振峰会引发系统的超调和振荡。考虑某些实际情形，若扰动变量频率为中频，则由于小型谐振峰值的存在导致扰动信号被放大，影响系统的正常稳定运行。在幅频特性曲线高频段，改进LADRC具有明显的反向谐振尖峰，即负谐振尖峰，约为-300 dB，对于高频噪声的抑制效果更佳显著，故改进LADRC具有更为优越的抗扰性能。在相频曲线中，由于传统LADRC存在正谐振峰，这导致了系统的相位滞后，约为250°，而由于改进LADRC具有负谐振尖峰，改善了系统的相位滞后，约为180°，提升了系统的动态响应效果。

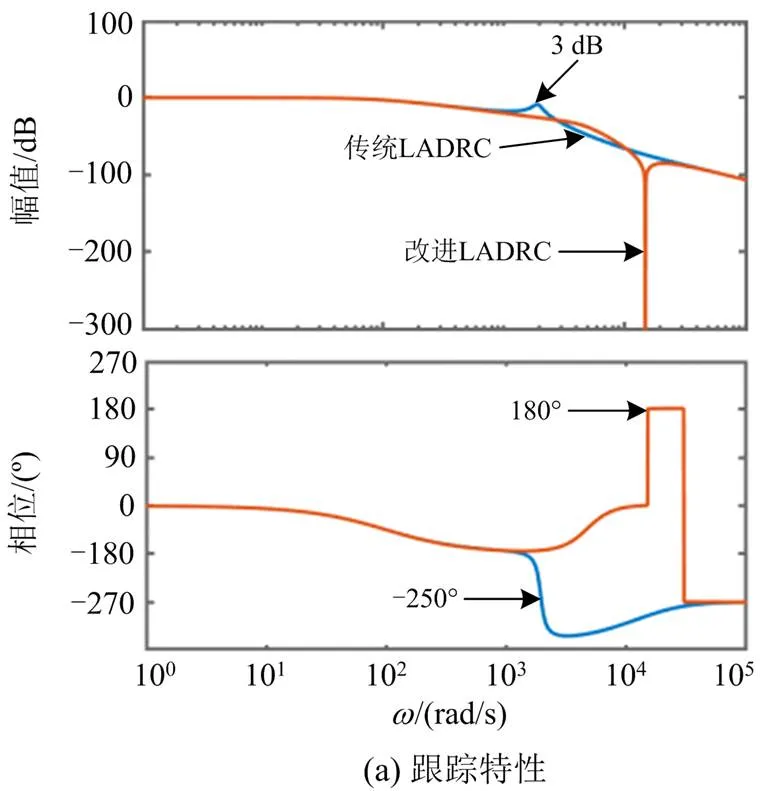
由图8(b)可知，两种控制策略下幅频特性曲线均位于0 dB以下，能够实现对电网背景电压的抑制。在高频段，两者基本重合，但改进LADRC具有一个正向谐振峰，考虑到系统扰动主要来自于电网背景电压，频率为基频，所以正向谐振峰不会对其产生影响。在低频段，改进LADRC明显低于传统LADRC，频率差值约为80 dB，因此，改进LADRC具有更理想的抗扰特性。在相频特性曲线中，传统LADRC由450°变化至90°，相位幅度为360°，而改进LADRC未发生变化，相位幅度为0°，相位变化明显小于传统LADRC，故改进LADRC具有更优越的动态响应效果。

基于以上对跟踪特性和抗扰特性的分析，相较于传统LADRC，改进LADRC表现出更为优越的性能，因此使用改进LADRC代替三相变流器系统中的传统矢量控制，可以获得更为理想的控制效果。

4 改进LADRC稳定性与性能分析

4.1 稳定性分析

改进LADRC的稳定性主要由改进LESO的稳定性决定，需对改进LESO进行稳定性分析。结合式(12)和拉式变换相关理论，可得到式(22)。

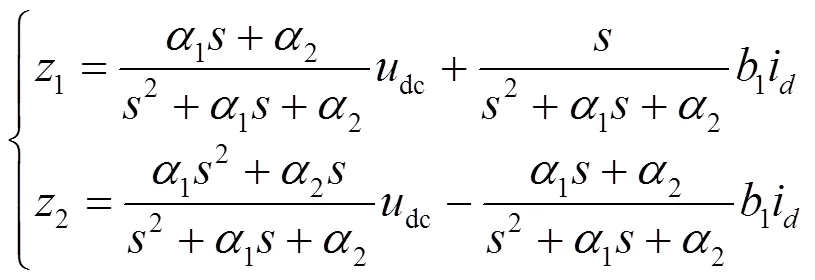
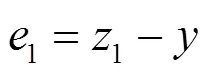
4.2 性能分析

改进LADRC的4个参数的改变会对系统的时域性能产生不同影响[18]，在实际系统控制中，需要从稳定性、快速性和抗扰性等多方面出发，对4种参数的选取进行比较，保证系统在具备稳定性的同时，提升其快速性和抗扰性。

5 仿真验证

为进一步验证此控制策略的正确性和优越性，在Matlab/Simulink仿真平台，搭建两级三相式光伏系统并网系统模型，在下述4种工况下进行验证。仿真参数见表1。

表1 系统参数

工况一：验证直流母线起始动态响应。

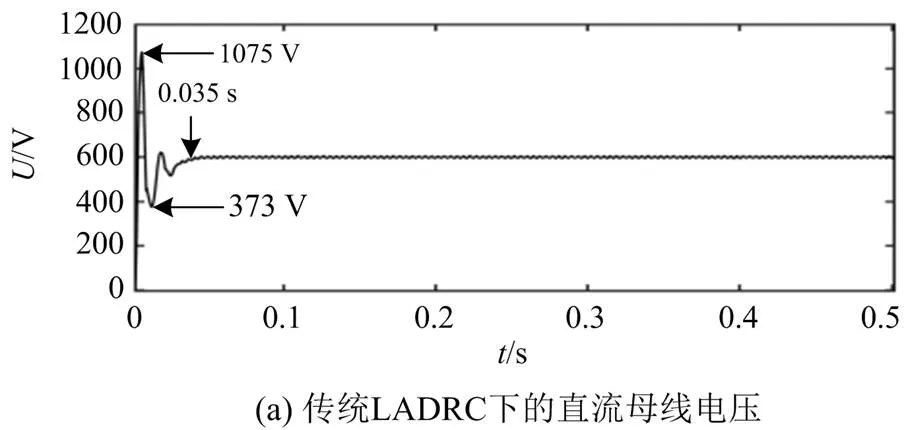
图13为两种控制策略下直流母线电压的动态情况，图13(a)为传统LADRC，最大电压为1025 V，电压最大突增量为425 V，最小电压为450 V，电压最小突减量为150 V，调节时间为0.055 s[19]。图13(b)为改进LADRC，最大电压为1075 V，电压最大突增量为475 V，最小电压为373 V，电压最小突减量为227 V，调节时间为0.035 s。在电压波动方面，改进LADRC优于传统LADRC，在快速性方面，传统LADRC优于改进LADRC，考虑到时间差0.02 s可忽略不计，因此改进LADRC具有更好的动态响应[20]。

工况二：验证光照强度降低时的动态响应。

图14为在1 s光伏系统的光照强度从1000 W/m2降低至500 W/m2时，直流母线电压的动态响应仿真曲线[21]。图14(a)展示了PI下的电压波动情形，电压呈现出振荡状态，电压最大跌落至500 V，升高至664 V，最大跌落量为100 V，最大升高量为64 V，调节时间为0.12 s。图14(b)展示了传统LADRC下的电压波动情形，电压最大跌落至560 V，跌落量为40 V，调节时间为0.02 s。图14(c)为改进LADRC控制下，电压在1 s时刻仅发生了微小的变化，因此从电压波动量和调节时间可以看出，改进LADRC拥有更为优越的扰动抵抗能力，即具有较好的抗扰性。

工况三：并网点电压波动时的动态响应。

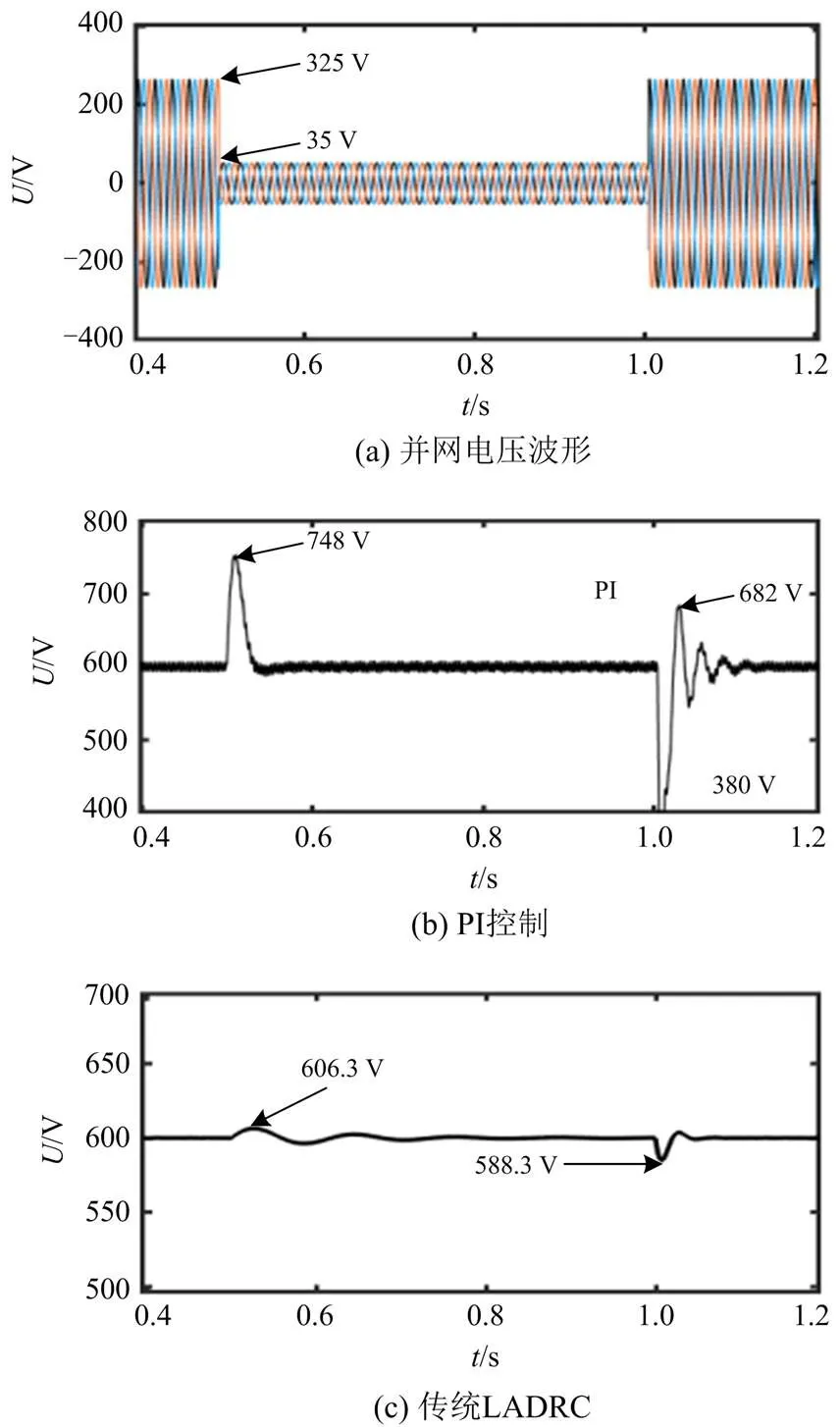
图15(a)为并网侧三相电压突变波形图，在0.5 s时，电压从325 V跌落至35 V，在1 s时，再次回到325 V[22]。图15(b)为PI控制下的直流母线电压波形图，在0.5 s，电压最大升高至748 V，振荡过长，即有超调和调节时间，在1 s时，电压最大降低至380 V，最大升高至682 V，存在超调和调节时间。传统LADRC控制下，在0.5 s时，电压波形存在振荡，最大振荡峰值为606.3 V，在1 s仅有最大降低量，为588.3 V，且调节时间明显小于PI。改进LADRC在0.5 s和1 s时电压无增量，且电压振荡程度明显降低，因此改进LADRC拥有更为优越的抗扰性能[23]。

工况四：验证并网处电流谐波含量。

为验证电流内环同样具有良好的控制效果，使用快速傅里叶变换(FFT)对并网侧A相电流进行验证[24]。图16中，PI的谐波畸变率(THD)为1.97%，传统LADRC为1.48%，改进LADRC为1.37%。经比较可得，改进LADRC具有较好的谐波抑制能力，增加并网成功的几率以及改善电能质量，减少了谐波造成的能量损耗，提高了系统整体的经济性[25]。

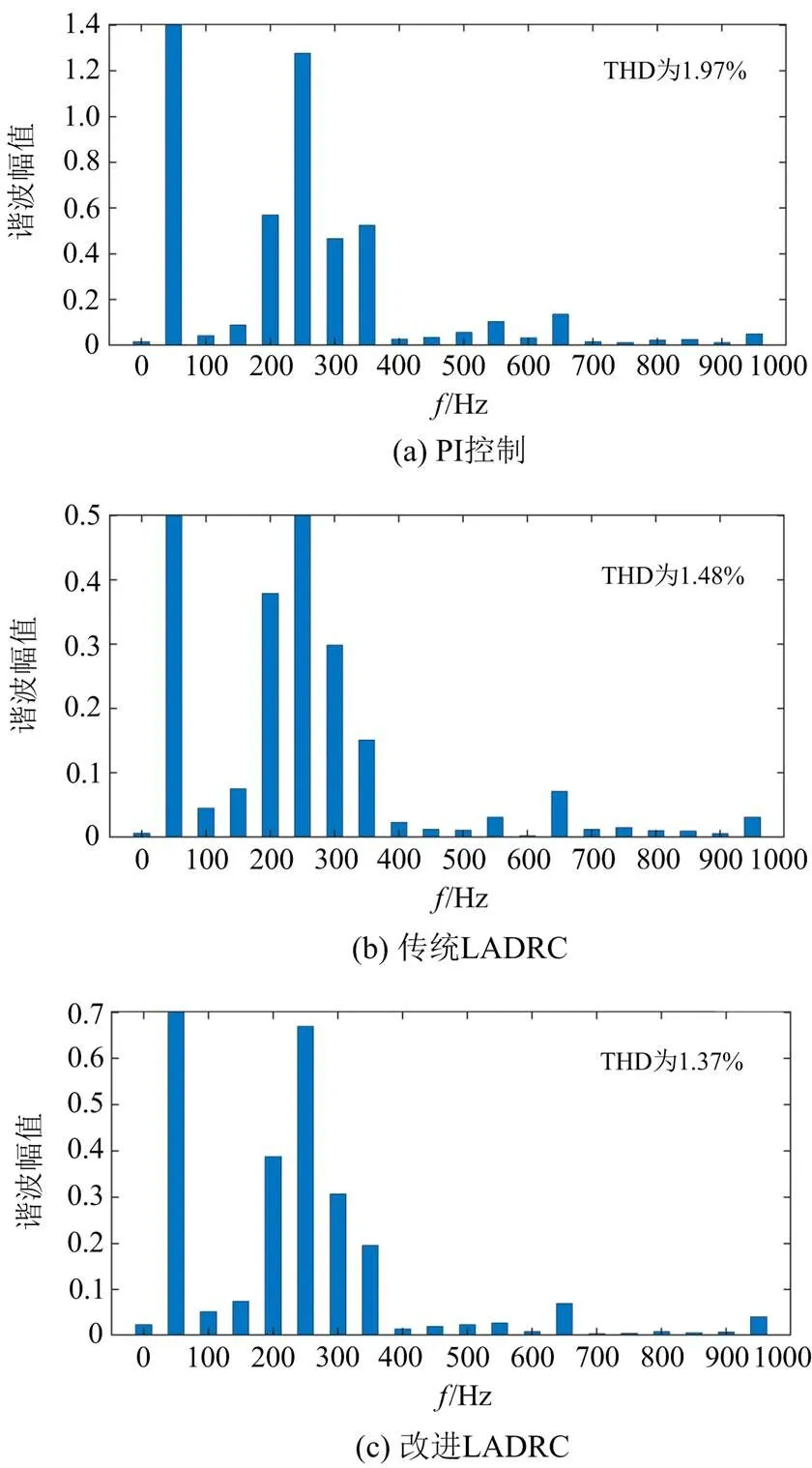
图16 3种控制策略下的A相电流THD

6 结论

本文以直流侧母线电压为研究对象，引入新型解耦方法，对线性扩张观测器进行改进，形成改进自抗扰控制，并与传统比例积分控制以及传统自抗扰控制进行仿真对比，可得到以下结论：

1) 改进自抗扰下的直流母线电压波动抑制效果更佳，保证了系统传输功率的平衡，从而提高了系统经济性；

2) 改进自抗扰既提高了系统的抗扰能力，又改善了系统的动态响应，具有更好的时域性能。

[1] 张沈习, 王丹阳, 程浩忠, 等. 双碳目标下低碳综合能源系统规划关键技术及挑战[J]. 电力系统自动化, 2022, 46(8): 189-207.

ZHANG Shenxi, WANG Danyang, CHENG Haozhong, et al. Key technologies and challenges of low-carbon integrated energy system planning for carbon emission peak and carbon neutrality[J]. Automation of Electric Power Systems, 2022, 46(8): 189-207.

[2] 谢运祥, 刘毓鑫, 关远鹏, 等. 三相LCL并网逆变器自适应模型预测控制策略[J]. 电机与控制学报, 2021, 25(4): 40-51.

XIE Yunxiang, LIU Yuxin, GUAN Yuanpeng, et al. Adaptive model predictive control for LCL three-phase grid-connected inverter[J]. Electric Machines and Control, 2021, 25(4): 40-51.

[3] WANG K, YUAN X. Stability analysis of the virtual inductance for LCL filtered droop-controlled grid- connected inverters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(3): 2685-2698.

[4] XIE Z, CHEN Y, WU W, et al. Admittance modeling and stability analysis of grid-connected inverter with LADRC- PLL[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 12272-12284.

[5] XU J, XIE S. LCL-resonance damping strategies for grid-connected inverters with LCL filters: a comprehensive review[J]. Journal of Modern Power Systems and Clean Energy, 2018, 6(2): 292-305.

[6] 韩永强, 徐明忻, 孙碣, 等. 改进LADRC的储能逆变器直流母线电压控制[J]. 电力系统及其自动化学报, 2021, 33(1): 13-21.

HAN Yongqiang, XU Mingxin, SUN Jie, et al. Improved DC bus voltage control of LADRC energy-storage inverter[J]. Proceedings of the CSU-EPSA, 2021, 33(1): 13-21.

[7] LIN P, WU Z, FEI Z, et al. A generalized PID interpretation for high-order LADRC and cascade LADRC for servo systems[J]. IEEE Transactions on Industrial Electronics, 2022, 69(5): 5207-5214．

[8] 陈超波, 王霞霞, 高嵩, 等. 基于区间滑模观测器的逆变器开路故障诊断方法[J]. 中国电机工程学报, 2020, 40(14): 4569-4579.

CHEN Chaobo, WANG Xiaxia, GAO Song, et al. A diagnosis method for open-circuit faults in inverters based on interval sliding mode observer[J]. Proceedings of the CSEE, 2020, 40(14): 4569-4579.

[9] 孙斌, 王海霞, 苏涛, 等. 永磁同步电机调速系统非线性自抗扰控制器设计与参数整定[J]. 中国电机工程学报, 2020, 40(20): 6715-6726.

SUN Bin, WANG Haixia, SU Tao, et al. Nonlinear active disturbance rejection controller design and tuning for permanent magnet synchronous motor speed control system[J]. Proceedings of the CSEE, 2020, 40(20): 6715-6726.

[10] ZHANG C H, LI X Y, ZHANG B X, et al. Modeling and mitigation of resonance current for modified LCL-type parallel inverters with inverter-side current control[J]. IEEE Transactions on Industrial Informatics, 2022, 18(2): 932-942.

[11] HOU X C, SUN K, ZHANG X, et al. A hybrid voltage/ current control scheme with low-communication burden for grid-connected series-type inverters in decentralized manner[J]. IEEE Transactions on Power Electronics, 2022, 37(1): 920-931.

[12] KUMAR A, ANWAR M, KUMAR S. Sliding mode controller design for frequency regulation in an interconnected power system[J]. Protection and Control of Modern Power Systems, 2021, 6(1): 77-88.

[13] 陈增强, 王永帅, 孙明玮, 等. 二阶非线性系统自抗扰控制的全局渐近稳定性[J]. 控制理论与应用, 2018, 35(11): 1687-1696.

CHEN Zengqiang, WANG Yongshuai, SUN Mingwei, et al. Global and asymptotical stability of active disturbance rejection control for second-order nonlinear systems[J]. Control Theory & Applications, 2018, 35(11): 1687-1696.

[14] KHAN A A, KHAN U A, AHMED H F, et al. Improved NPC inverters without short-circuit and dead-time issues[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 2180-2190.

[15] WANG Q, JIANG X H, WANG Y Z. An efficient three-phase resonant pole inverter with low conduction loss of switching devices[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2022, 69(3): 1512-1516.

[16] 王武, 雷文浩, 蔡逢煌, 等. 结合电流应力优化的双有源全桥DC-DC变换器自抗扰控制[J]. 电工技术学报, 2022, 37(12): 3073-3086.

WANG Wu, LEI Wenhao, CAI Fenghuang, et al. Active disturbance rejection control of dual-active-bridge DC-DC converter with current stress optimization[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3073-3086.

[17] 金辉宇, 张瑞青, 王雷, 等. 线性自抗扰控制参数整定鲁棒性的根轨迹分析[J]. 控制理论与应用, 2018, 35(11): 1648-1653.

JIN Huiyu, ZHANG Ruiqing, WANG Lei, et al. Root locusanalysis on parameter tuning robustness of linear active disturbance rejection control[J]. Control Theory & Application, 2018, 35(11): 1648-1653.

[18] CAO W C, MA Y W, WANG F, et al. Low-frequency stability analysis of inverter-based islanded multiple-bus AC microgrids based on terminal characteristics[J]. IEEE Transactions on Smart Grid, 2020, 11(5): 3662-3676.

[19] 付子义, 张字远, 董彦杰. 弱电网条件下LCL型三相光伏并网逆变器研究[J]. 太阳能学报, 2021, 42(4): 193-199.

FU Ziyi, ZHANG Ziyuan, DONG Yanjie. LCL type three-phase photovoltaic grid-connected inverter under week grid conditions[J]. Acta Energiae Solaris Sinica, 2021, 42(4): 193-199.

[20] ZHOU W Y, WANG M Q, WU Q F. A model-based monitoring method for offline accelerated testing of DC-link capacitor in three-phase inverter systems[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 61-67.

[21] 王翰文, 曾成碧, 苗虹. 基于多谐振电网电压前馈的并网逆变器相位补偿算法研究[J]. 电力系统保护与控制, 2021, 49(18): 81-89.

WANG Hanwen, ZENG Chengbi, MIAO Hong. A phase compensation algorithm of a grid-connected inverter based on a feedforward multi-resonant grid voltage[J]. Power System Protection and Control, 2021, 49(18): 81-89.

[22] 姚欢, 史婷娜, 王志强, 等. 级联H桥逆变器驱动永磁同步电机的鲁棒预测电流控制策略[J]. 中国电机工程学报, 2022, 42(14): 5266-5278.

YAO Huan, SHI Tingna, WANG Zhiqiang, et al. Robust predictive current control for PMSM fed by CHB inverter[J]. Proceedings of the CSEE, 2022, 42(14): 5266-5278.

[23] 刘人志, 陈卓, 唐文博, 等. 弱电网下计及锁相环影响的LCL型并网逆变器控制策略[J]. 电力系统保护与控制, 2022, 50(5): 178-187.

LIU Renzhi, CHEN Zhuo, TANG Wenbo, et al. Control strategy of an LCL type grid-connected inverter with the influence of a phase-locked loop under a weak power grid[J]. Power System Protection and Control, 2022, 50(5): 178-187.

[24] 于晶荣, 孙文, 于佳琪, 等. 基于惯性自适应的并网逆变器虚拟同步发电机控制[J]. 电力系统保护与控制, 2022, 50(4): 137-144.

YU Jingrong, SUN Wen, YU Jiaqi, et al. Virtual synchronous generator control of a grid-connected inverter based on adaptive inertia[J]. Power System Protection and Control, 2022, 50(4): 137-144.

[25] 马也, 史丽萍, 李衡, 等. 基于VSG控制的微网逆变器工频振荡现象研究[J]. 电力系统保护与控制, 2022, 50(1): 107-115.

MA Ye, SHI Liping, LI Heng, et al. Power frequency oscillation of a microgrid inverter based on VSG control[J]. Power System Protection and Control, 2022, 50(1): 107-115.

DC bus voltage fluctuation suppression strategy of a converter system based on improved active disturbance rejection

ZHOU Xuesong, GUO Shuaichao, MA Youjie, LI Yuechao, MA Chuang

(School of Electrical and Electronic Engineering, Tianjin University of Technology, Tianjin 300384, China)

When it comes to DC bus voltage fluctuation, a photovoltaic grid-connected converter system is prone to suffer from unbalanced power transmission and unstable operation at the input and output. Thus an improved linear active disturbance rejection control strategy is proposed. First, the physical and mathematical models of the converter system are established, and the principle of energy transmission imbalance is analyzed. Then, a first-order linear active disturbance rejection controller is designed to replace the traditional proportional integral vector controller. Further, in order to strengthen the disturbance observation ability of the extended observer, a new parameter decoupling method is introduced to form a decoupling improved active disturbance rejection control. This improves the speed and disturbance rejection of the system. Finally, based on the frequency response characteristic curve and a variety of simulation conditions, a simulation is carried out. The results show that, compared with the traditional control strategy, the improved linear ADRC not only is superior in suppressing voltage fluctuation of the DC side bus, but also has good disturbance resistance and short-time transient fault ride-through ability. This ensures power transmission balance and normal and stable operation of the system.

improved active disturbance rejection control; DC bus voltage; observer; PI control; parameter decoupling

10.19783/j.cnki.pspc.220452

国家自然科学基金项目资助(51877152)

This work is supported by the National Natural Science Foundation of China (No. 51877152).

2022-03-30；

2022-08-25

周雪松(1964—)，男，博士，教授，研究方向为新能源发电、电力系统控制；E-mail: zxs2020sjteam@126.com

郭帅朝(1997—)，男，通信作者，硕士研究生，研究方方向为电力系统保护、智能电网。E-mail: shuaichao8253@ 126.com

(编辑 许 威)