质心径向可变球形机器人多运动模式的运动特性对比研究

马 龙

(1.煤炭科学技术研究院有限公司，北京 100013；2.煤炭资源高效开采与洁净利用国家重点实验室，北京 100013)

球形机器人的特殊外形与运动方式使其具备防倾覆与自我保护的能力，同时具备高运动效率与低能耗的优势[1-2]。基于摆式偏心力矩驱动机制的球形机器人机构复杂度低并且驱动效率高，是目前研究广泛的球形机器人类型[3]。针对基于摆式偏心力矩驱动机制的球形机器人，通过增大重摆在球壳内部的活动范围，使重摆在具备周向运动能力的同时具备径向运动的能力，不仅能够使球形机器人实现传统的重摆驱动模式，同时还能够实现新型的倒立摆驱动模式(如图1所示)，且重摆在2种不同驱动模式下的径向移动能够使球形机器人的运动状态呈现出不同的特点。

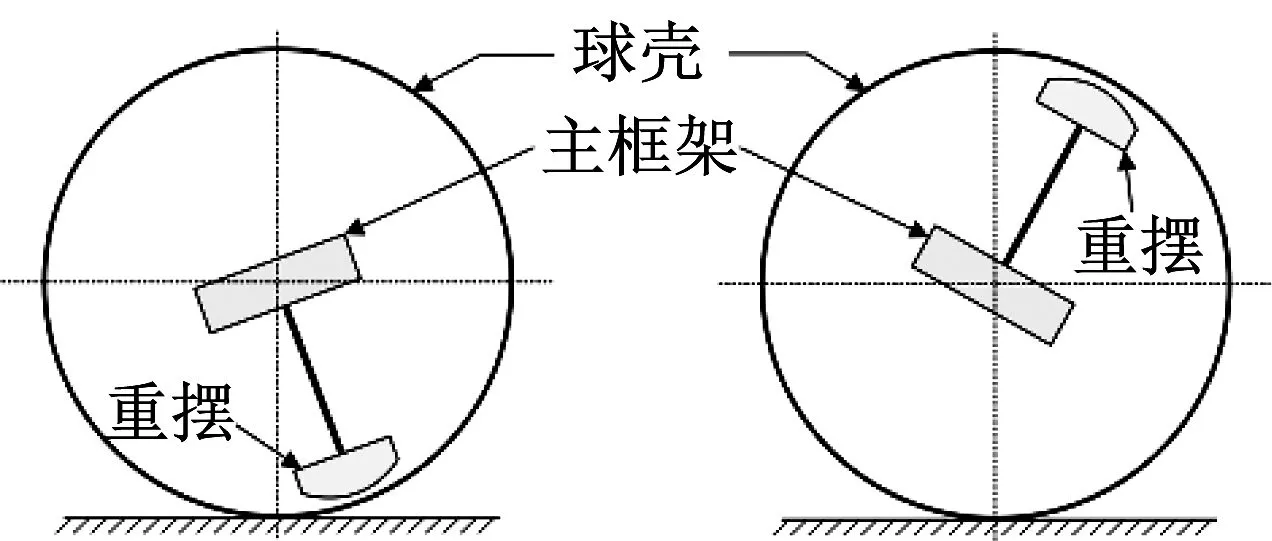
(a) 重摆驱动模式 (b) 倒立摆驱动模式

面向非结构化任务环境时，倒立摆驱动模式与质心径向可变能力对丰富球形机器人的驱动方式以及提升球形机器人的实用性有极大的促进作用，然而倒立摆驱动能够对球形机器人的运动能力、控制性能以及能耗水平等方面的运动特性产生影响。将不同驱动模式以及不同质心径向位置情况下的运动特性融入球形机器人的实际使用需求中，对球形机器人实用性提升有重要意义。

本文针对质心径向可变球形机器人，讨论了不同驱动模式、不同摆长状态、不同运动速度以及不同坡度情况对球形机器人的运动能力、控制性能与能耗水平3方面运动特性产生的影响，并根据实验结果对质心径向位置与球形机器人运动特性需求之间的关联模型展开研究，为面向不同任务需求时质心径向可变球形机器人的驱动模式与质心位置的选择提供依据。

1 实验平台与研究路线

本文以重摆驱动模式作为对比，以BYQ-GS型质心径向可变球形机器人作为实验平台，基于面向非结构化任务环境的空间多体动力学模型，运用分层滑模控制(hierarchical sliding mode control,HSMC)方法探索倒立摆驱动与质心径向变化情况下球形机器人运动特性，并开展质心径向位置与球形机器人运动需求的关联模型研究。

1.1 实验平台

实验平台采用BYQ-GS型质心径向可变球形机器人如图2(a)与图2(b)所示，该球形机器人可实现重摆机构处于内部机构下端与内部机构上端2种位置的转换如图2(c)与图2(d)所示，基于2种不同重摆位置分别实现重摆驱动与倒立摆驱动，以及不同驱动模式下的径向变化动作。

(a) 内部机构

BYQ-GS型球形机器人基本性能如表1所示。球壳选用厚度为2.3 mm、外径为400 mm、铺层顺序为[0/90]6的玻璃纤维增强聚合物复合材料球壳；控制系统采用上位机发送指令，移动端负责接收、运算与执行指令，并将运动过程中相关传感器产生的实时位姿数据传送至上位机的形式；位姿反馈系统由电机编码器、MTi-300型惯性航姿测量系统(inertial measurement unit,IMU)、BD992-INS型多星多频高精度组合导航板卡(real time kinematic,RTK)组成，其中IMU角度测量精度为0.05°，RTK理论定位精度为0.008 m，速度测量精度为0.007 m/s，俯仰/翻滚角度测量精度为0.10°，可实现全局位置、航向、速度、姿态的实时信息获取，解算后可得其运动状态信息[4-6]。

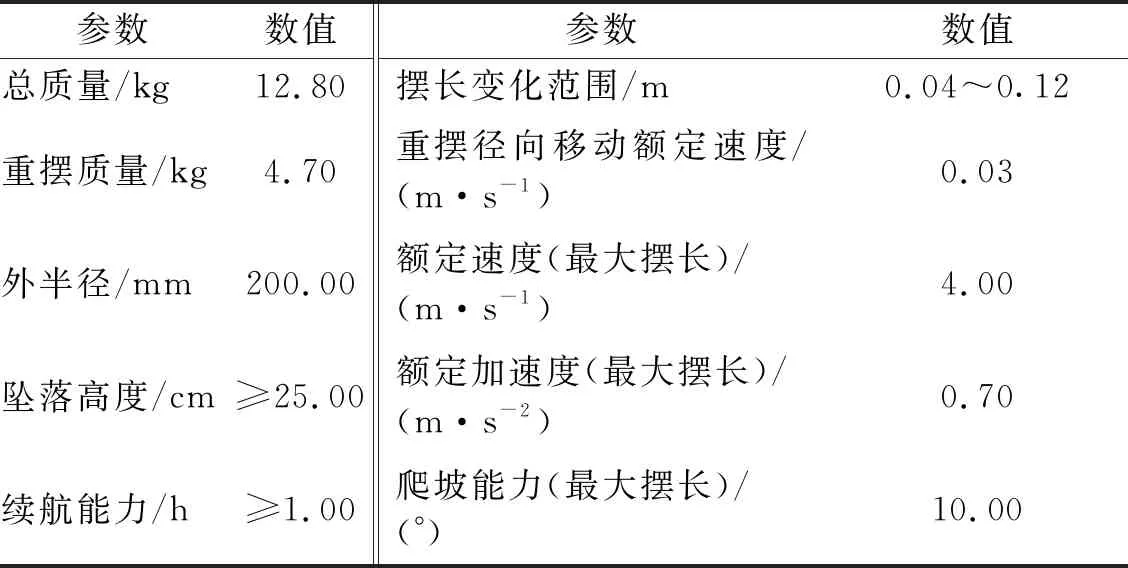
表1 BYQ-GS型球形机器人样机的性能参数

1.2 动力学模型

质心径向可变球形机器人在2种驱动模式下的全方位多体运动简化模型如图3所示，定义模式1为重摆驱动模式，模式2为倒立摆驱动模式。

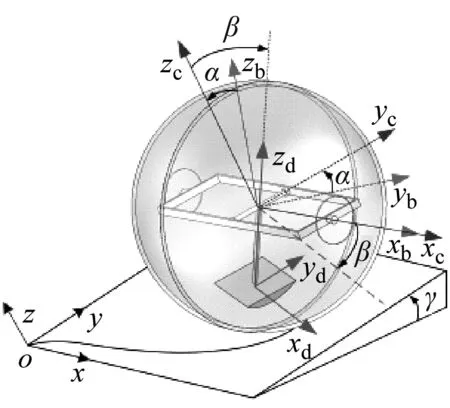
(a) 模式1：重摆驱动模式

Σ0为坡面固连惯性坐标系，Σb为球壳固连坐标系且随之滚动，Σc为主框架固连坐标系且随之转动，Σb与Σc的坐标原点均与球壳几何中心重合；Σd为重摆固连坐标系且随之转动，原点为重摆的质心；xc与xb始终重合且同向，yd与xb始终同向。初始状态下Σc与Σb重合，主框架绕xb转动，转角为α；Σd与Σc各轴平行，重摆绕yc转动，转角为β；坡面倾角为γ；从Σ0到Σb的zyx欧拉角分别表示为(φ,θ,Ψ)，φ为航向角，θ为横滚角，Ψ为俯仰角。球壳几何中心在Σ0中的坐标为(x,y,z)，半径为R，2种驱动模式下的可变摆长为L，长轴电机和短轴电机在xc和yc方向力矩分别为τΨ和τθ，重摆提升电机在zd方向力矩为τL。

质心径向可变球形机器人的摆长L为变量之一，球形机器人的位置、姿态与质心位置可由式(1)所示q中8个广义坐标进行完整描述，3个非完整约束可表示为式(1)所示矩阵形式[7-8]

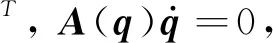
A(q)=[A1⋮A2]=

(1)

根据第一类拉格朗日方程，理想任务环境下处于重摆驱动模式(i=1)与倒立摆驱动(i=2)模式的质心径向可变球形机器人动力学模型为

(2)

式中：Mi(q)∈8×8为惯性矩阵;8×1为非线性项;λ=[λ1λ2λ3]T为与非完整约束对应的待定乘子向量;τ=[τθτΨτL]T为控制输入力矩向量，定义P为直线模组丝杠导程，输入变换矩阵Ei(q)可表示为

为消除非完整约束对动力学模型构建产生的影响，设定球形机器人系统输出变量q3，理想任务环境下质心径向可变球形机器人处于重摆驱动模式(i=1)与倒立摆驱动模式(i=2)时的动力学模型可转换为

CTEiτ

(3)

其中,质心径向可变球形机器人处于状态空间中的任何位置，矩阵Δ均为可逆矩阵，且

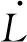
τ+τfx+τfn+τdv+τdu=τ+τfc+τξ

(4)

式中：τm为电机输出力矩;τf为运动摩擦项;τd为机构或外界环境扰动。根据扰动是否可控，将τd分为可控τdv与不可控τdu，将τf分为线性τfx与非线性τfn。将τdv与τfx用可控补偿力矩τfc表示，其主要来自地面对球壳的滚动摩阻力偶矩与轴承黏性阻尼导致的关节内部摩擦力矩；将τdu与τfn用不确定因素τξ表示。

由式(4)可知，面向非结构化环境的球形机器人进行控制需考虑与球形机器人自身相关的参数、运动过程中的可控因素以及运动过程中的不确定与不可控因素。用ξ[t,u(t)]表示包含不可控的有界未知扰动与非线性摩擦等不确定因素的不确定项。将式(4)转换为式(5)所示形式，进一步表示为式(6)所示子系统状态空间表达式，广义坐标i∈(x,y,α,β)[9]。

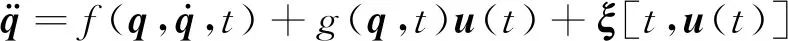
(5)

g(q,t)=(g1…gi)T=M(q)-1,

u(t)=(u1…ui)T=τ+τfc,

ξ[t,u(t)]=(ξ1…ξi)T

(6)

1.3 运动特性评价指标

实验设置3个不同场景：场景1为水平面不同期望速度场景下的直线运动(如图4(a)所示)，场景2为不同坡面角度恒定期望速度场景下的直线运动(如图4(b)所示)，场景3为不同坡面角度场景下的全方位运动(如图4(c)所示)。不同速度状态下的实验环境为室外田径跑道，不同坡度状态下的实验环境为室内尺寸为2.5 m×2.5 m木质坡面，通过调整坡面下方木质垫块数量与位置可实现坡面角度调节。

(a)

运动特性的评价指标设置如图5所示。分别从直线运动与全方位运动2种基本的运动形式出发，针对传统重摆驱动模式(i=1)以及新型倒立摆驱动模式(i=2)，对球形机器人的运动能力、控制性能以及能耗水平3个方面运动特性展开分析研究。

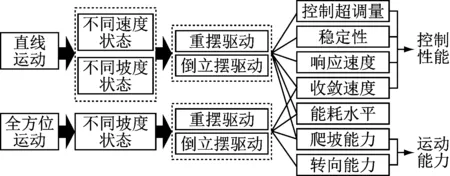
图5 运动特性评价标准

针对直线运动：统计指标的获取基于球壳运动位置误差ex(t)=px(t)-x(t)数据以及重摆摆动位置误差eα(t)=pα(t)-α(t)数据，其中:px(t)与pα(t)为实时位置的理论值;x(t)与α(t)为实时位置的实际值。运用模式i的运动收敛时间tri衡量控制系统收敛速度，运动收敛状态能够通过式(7)进行判定；运用模式i运动未收敛时位置误差的最大绝对值|ex|maxi与|eα|maxi衡量控制超调量；运用模式i运动未收敛时位置误差的均方根误差ex-rmsei与eα-rmsei衡量控制稳定性；运用模式i运动过程中最大力矩产生时间tτ-maxi衡量控制系统响应速度。

-0.1|emax-emin|≤e≤0.1|emax-emin|

(7)

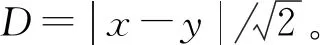
运用式(8)所示驱动电机在指定区间范围内每个采样周期平均输出功率Pi对能耗水平进行衡量

(8)

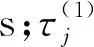
为得到倒立摆驱动模式下球形机器人运动特性变化趋势，以重摆驱动模式为对比对象，对上述统计指标比值变化情况进行分析，相关计算公式如式(9)所示

(9)

1.4 控制器参数设定

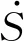
式中，ei(t)为广义坐标期望值pi(t)与实时值i(t)之差，i∈(x,y,α,β)。不同场景下控制器参数设置，如表2[11-12]所示。

表2 不同场景下的控制器参数

2 运动特性分析

运动初始阶段将摆长L设置为如式(10)所示不同值，且运动过程中摆长保持恒定，作为2种不同驱动模式下球形机器人运动特性的研究前提。由于运动过程受到滚动摩阻力偶矩影响，运动收敛状态下的理论摆起平衡角pα与pβ可由于涛的研究与文献[13]对重摆摆起平衡角的描述相结合进行确定。

L=0.04+0.02n1, 0≤n1≤4,n1∈N

(10)

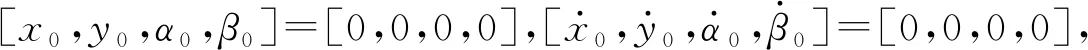
vd∈{0.2,0.5,0.8,1.0,1.2,1.4,1.6}

(11)

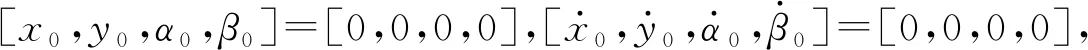
γ∈{0°,1°,2°,3°,4°,6°,8°,10°}

(12)

为保证数据可靠性的同时对实验结果进行直观观察对比，采用重复进行5次实验并取其数据平均值，运用Savizkg-Golag平滑算法(40点2次)对实验数据进行预处理，作为实验最终数据[14]。

采用式(13)对不同指标构建的数学模型进行归一化，即把数据映射到(0,1)范围内进行处理，在保留原始数据分布的同时使相关指标变化规律具有普适性，并消除关联模型构建过程中不同指标的量纲影响[15]。

Norm(z)=(z-zmin)/(zmax-zmin)

(13)

运用最小二乘法对实验所得的n个数据进行拟合，根据误差理论分析方法，坐标点拟合值f(xi,yi)相对于实际值zi的精度用式(14)[16-17]进行表示。

(14)

2.1 控制性能分析

控制性能评价指标包括控制系统收敛速度、超调量、稳定性与响应速度，分别对每项指标对应统计量变化情况进行分析，运用最小二乘法对实验数据进行公式化拟合(待定系数小数位为2)，建立其数学模型，并根据式(14)计算数学模型的拟合精度。

2.1.1 指标1：收敛速度(统计指标：收敛时间tr)

场景1：对不同摆长L与期望速度vd进行组合，2种不同模式下的收敛时间tr1与tr2的变化趋势如图6所示(黑色符号为实验数据)。

当2种驱动模式下球形机器人摆长L与期望速度vd均保持一致时，0.48 s≤tr2-tr1≤6.03 s，即收敛速度方面倒立摆驱动模式与重摆驱动模式相比具有劣势。

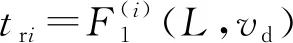
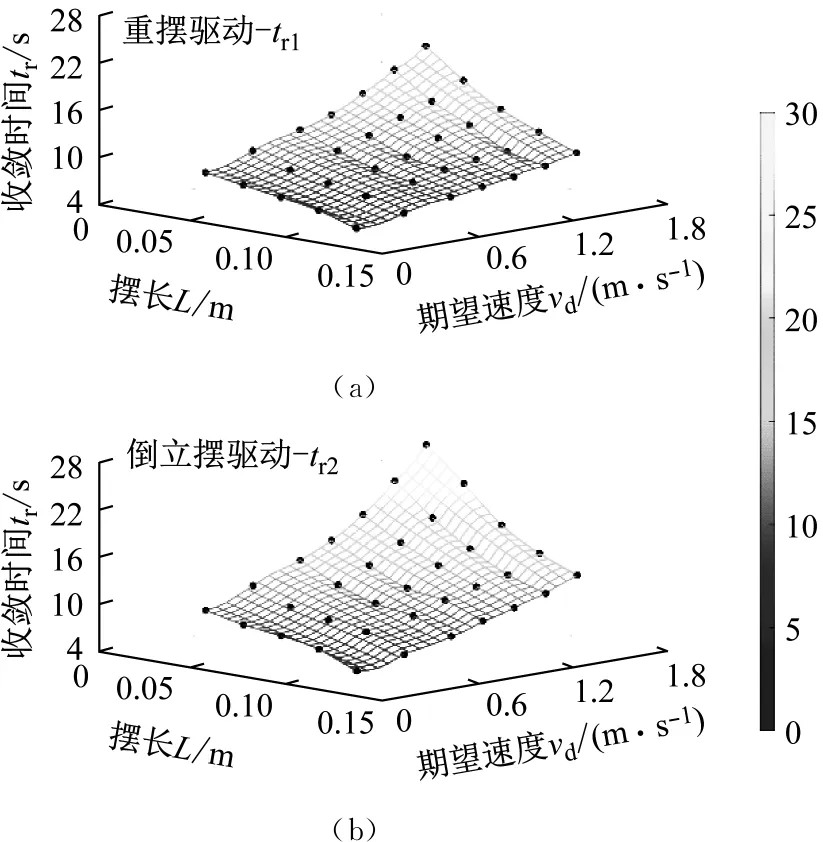
图6 场景1情况下tr的变化趋势图

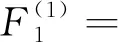
108.19Lvd+24.64,

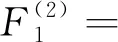
163.14Lvd+28.88

(15)

场景2：对不同摆长L与坡面角度γ进行组合，2种不同模式下的收敛时间tr1与tr2的变化趋势如图7所示(黑色符号为实验数据)。

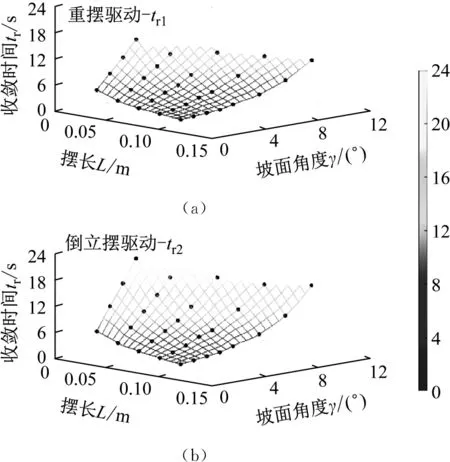
图7 场景2情况下tr的变化趋势图

当2种驱动模式下球形机器人摆长L与坡面角度γ均保持一致时，0.61 s≤tr2-tr1≤6.30 s，即收敛速度方面倒立摆驱动模式与重摆驱动模式相比具有劣势。

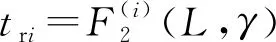
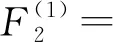
436.34L+7.06γ+356.04L2γ-1.29Lγ2-

99.20Lγ+20.08,

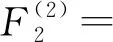
457.49L+8.31γ+418.84L2γ-1.32Lγ2-

116.84Lγ+21.58

(16)

场景3：对不同摆长L与坡面角度γ进行组合，2种不同模式下的收敛时间tr1与tr2的变化趋势如图8所示(黑色符号为实验数据)。

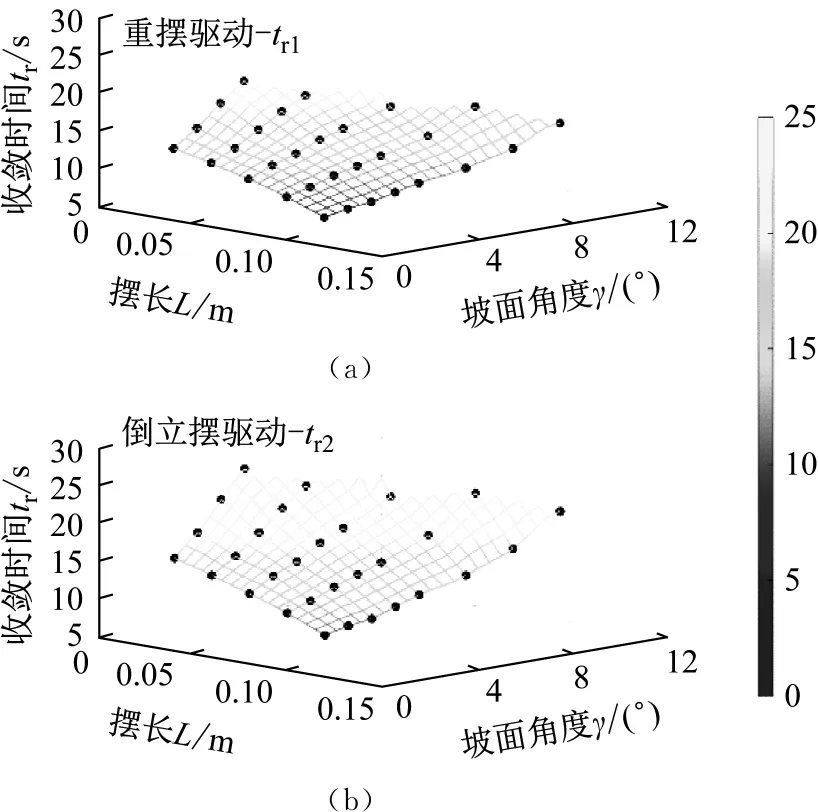
图8 场景3情况下tr的变化趋势图

当2种驱动模式下球形机器人摆长L与坡面角度γ均保持一致时，2.45 s≤tr2-tr1≤8.84 s，即收敛速度方面倒立摆驱动模式与重摆驱动模式相比具有劣势。

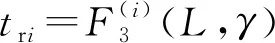
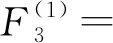
160.63L+4.27γ+203.47L2γ-0.38Lγ2-

53.84Lγ+18.82,

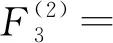
232.66L+6.45γ+297.41L2γ-0.42Lγ2-

80.33Lγ+23.73

(17)

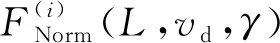
(18)

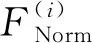
2.1.2 指标2：控制超调量(统计指标：运动未收敛时位置误差的最大绝对值)|ex|max

场景1：对不同摆长L与期望速度vd进行组合，2种不同模式下球壳运动位置误差的最大绝对值|ex|max1与|ex|max2，以及重摆摆动位置误差的最大绝对值|eα|max1与|eα|max2变化趋势,如图9所示(黑色符号为实验数据)。

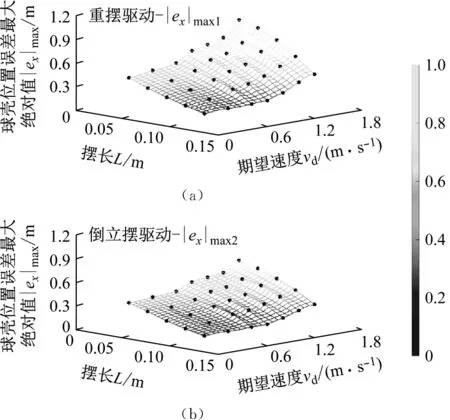
图9 场景1情况下|e|max的变化趋势图

当2种驱动模式下球形机器人的摆长L与期望速度vd均保持一致时，0.031 m≤|ex|max1-|ex|max2≤0.249 m，0.038 rad≤|eα|max1-|eα|max2≤0.195 rad，即控制超调量方面倒立摆驱动模式与重摆驱动模式相比具有优势。

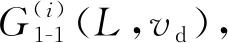
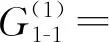
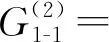
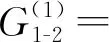
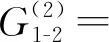
(19)

场景2：对不同摆长L与坡面角度γ进行组合，2种模式下球壳运动位置误差的最大绝对值|ex|max1与|ex|max2，以及重摆摆动位置误差的最大绝对值|eα|max1与|eα|max2变化趋势,如图10所示(黑色符号为实验数据)。

当2种驱动模式下球形机器人的摆长L与坡面角度γ均保持一致时，0.023 m≤|ex|max1-|ex|max2≤0.142 m，0.022 rad≤|eα|max1-|eα|max2≤0.235 rad，即控制超调量方面，倒立摆驱动模式与重摆驱动模式相比具有优势。

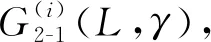
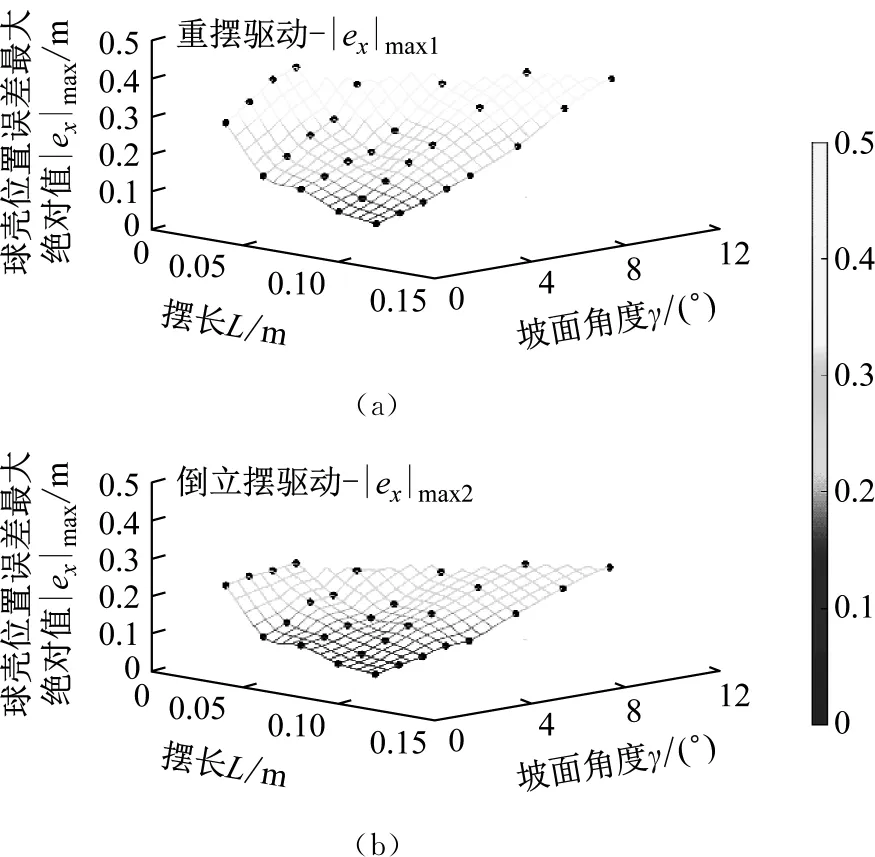
图10 场景2情况下|e|max的变化趋势图

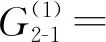
0.05γ-2.38L2γ-0.01Lγ2-0.61Lγ+0.62,

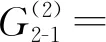
0.03γ-1.17L2γ-0.02Lγ2-0.32Lγ+0.43,

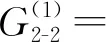
0.23γ+17.99L2γ-0.05Lγ2-4.02Lγ+0.93,

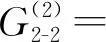
0.13γ+8.46L2γ-0.02Lγ2-2.03Lγ+0.61

(20)

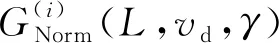
(21)

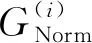
2.1.3 指标3：控制稳定性(统计指标：运动未收敛时位置误差的均方根误差ermse)

场景1：对不同摆长L与期望速度vd进行组合，2种不同模式球壳运动位置误差的均方根误差ex-rmse1与ex-rmse2，以及重摆摆动位置误差的均方根误差eα-rmse1与eα-rmse2与变化趋势,如图11所示(黑色符号为实验数据)。

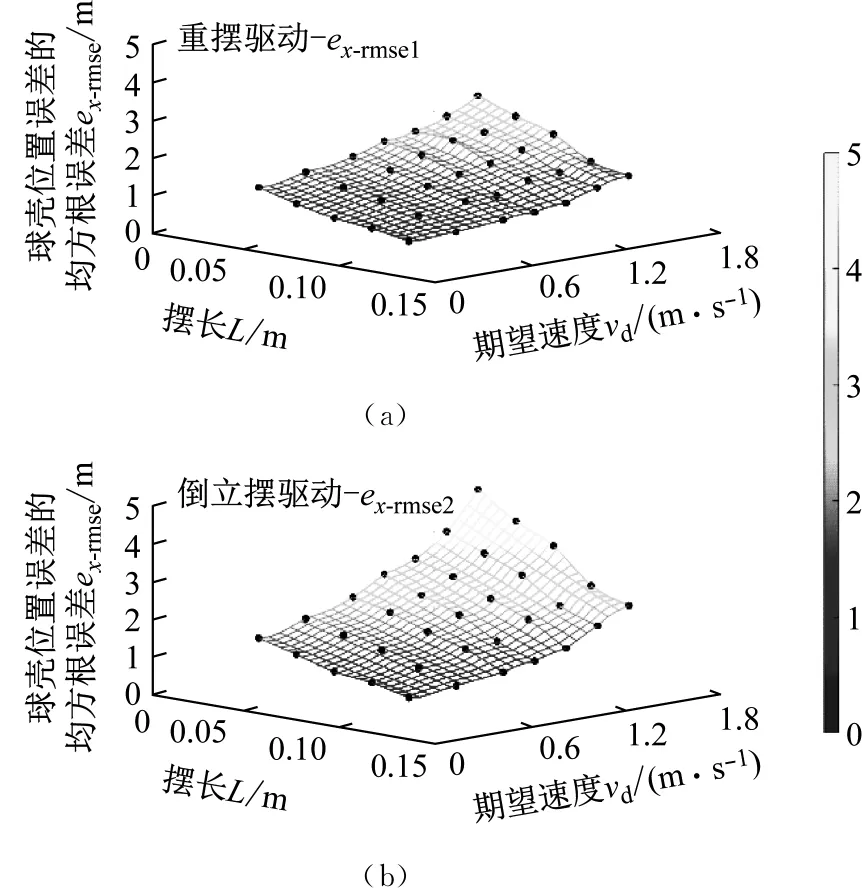
图11 场景1情况下ermse的变化趋势图

当2种驱动模式下球形机器人的摆长L与期望速度vd均保持一致时，0.109 m≤ex-rmse2-ex-rmse1≤1.721 m，0.026 rad≤eα-rmse2-eα-rmse1≤0.154 rad，即控制稳定性方面，倒立摆驱动模式与重摆驱动模式相比具有劣势。

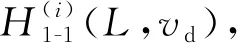
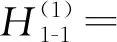
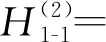
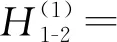
(22)

场景2：对不同摆长L与坡面角度γ进行组合，2种不同模式下球壳运动位置误差的均方根误差ex-rmse1与ex-rmse2，及重摆摆动位置误差的均方根误差eα-rmse1与eα-rmse2变化趋势,如图12所示(黑色符号为实验数据)。

当2种驱动模式下球形机器人的摆长L与坡面角度γ均保持一致时，0.079 m≤ex-rmse2-ex-rmse1≤0.602 m,0.020 rad≤eα-rmse2-eα-rmse1≤0.149 rad,即控制稳定性方面倒立摆驱动模式与重摆驱动模式相比具有劣势。

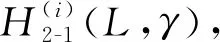
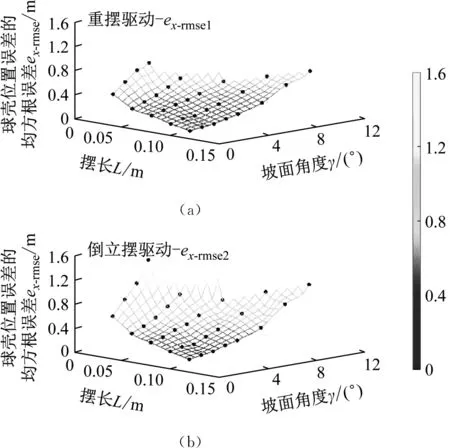
图12 场景2情况下ermse的变化趋势图

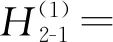
0.14γ+10.45L2γ+0.01Lγ2-2.35Lγ+0.75,

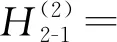
29.85L+0.20γ+15.99L2γ+0.01Lγ2-

3.54Lγ+1.05,

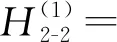
0.02γ+1.91L2γ-0.01Lγ2-0.42Lγ+0.08,

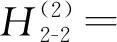
0.03γ+2.56L2γ-0.01Lγ2-0.56Lγ+0.10

(23)

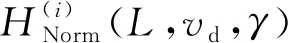
(24)

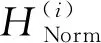
2.1.4 指标4：控制系统响应速度(统计指标：最大力矩产生时间tτ-max)

场景1：对不同摆长L与期望速度vd进行组合，2种不同模式下的收敛时间tτ-max1与tτ-max2的变化趋势,如图13所示(黑色符号为实验数据)。

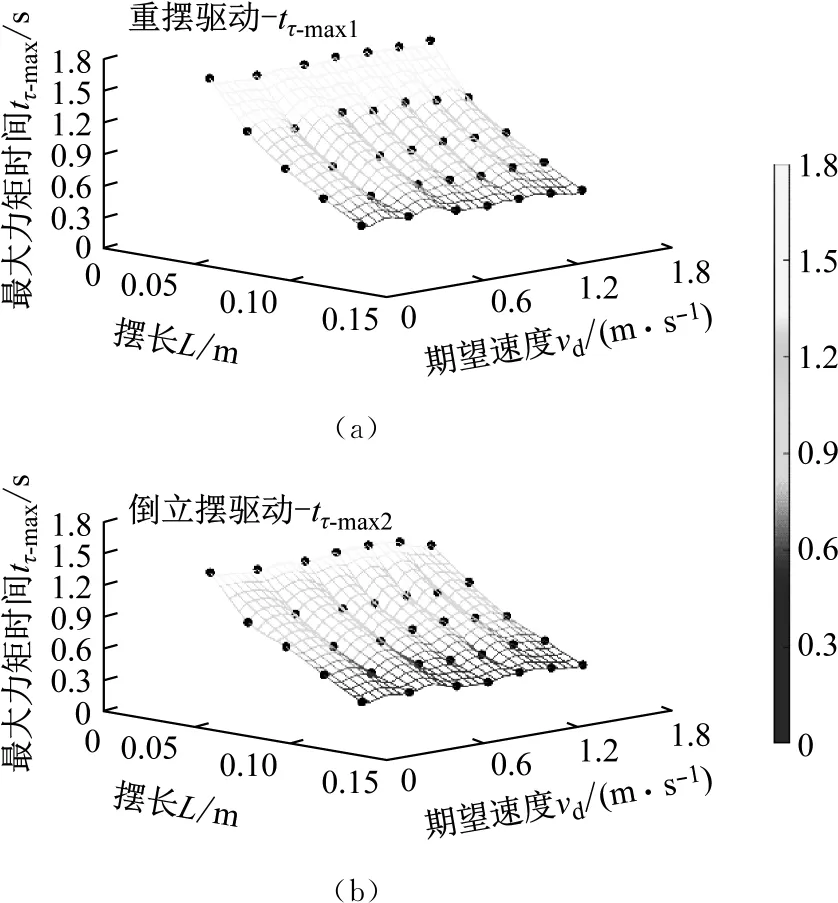
图13 场景1情况下tτ-max的变化趋势图

当2种驱动模式下球形机器人的摆长L与期望速度vd均保持一致时，0.10 s≤tτ-max1-tτ-max2≤0.39 s，即控制系统响应速度方面倒立摆驱动模式与重摆驱动模式相比具有优势。

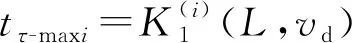
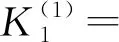
0.16Lvd+3.14,

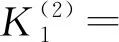
0.17Lvd+2.88

(25)

场景2：对不同摆长L与坡面角度γ进行组合，2种不同模式下的收敛时间tτ-max1与tτ-max2的变化趋势,如图14所示(黑色符号为实验数据)。

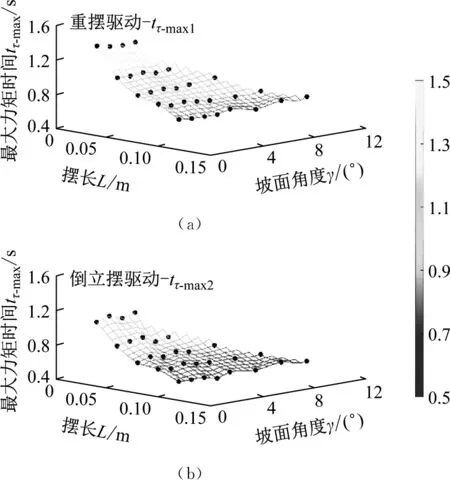
图14 场景2情况下tτ-max的变化趋势图

当2种驱动模式下球形机器人的摆长L与坡面角度γ均保持一致时，0.12 s≤tτ-max1-tτ-max2≤0.32 s，即控制系统响应速度方面倒立摆驱动模式与重摆驱动模式相比具有优势。

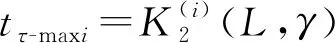
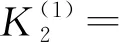
45.27L-0.03γ-6.28L2γ-0.02Lγ2+

1.11Lγ+2.72,

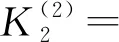
37.57L+0.01γ-0.58L2γ-0.03Lγ2+

0.12Lγ+2.19

(26)

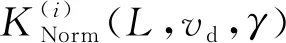
(27)

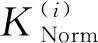
2.2 运动能力分析

运动能力评价指标包括爬坡能力和转向能力，分别对每项指标对应统计量变化情况进行分析，运用最小二乘法对实验数据进行公式化拟合(待定系数小数位为2)，建立其数学模型，并根据式(14)计算数学模型的拟合精度。

2.2.1 指标1：爬坡能力

根据2.1节控制性能分析部分所示实验数据，在不同坡面角度恒定期望速度下的直线运动实验以及不同坡面角度下的全方位运动实验中，摆长L与最大坡面角度γ对应情况,如图15所示。

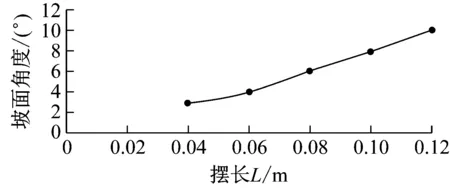
图15 不同摆长情况下对应爬坡能力的坡面角度

当BYQ-GS型球形机器人样机的运动能够收敛时，倒立摆驱动模式与重摆驱动模式下球形机器人爬坡能力相同；随摆长L从0.04 m逐渐变化至0.12 m时，最大爬坡角度从3°逐渐提升至10°。

对图15所示实验数据进行公式化拟合，式(28)为摆长L与最大爬坡角度γ的数学模型拟合结果。根据式(14)可得A(L)对实验数据的拟合精度为0.085°，该拟合精度不影响实验数据趋势判断。

γ=A(L)=-10 416.67L3+2 857.14L2-

152.98L+5.20

(28)

爬坡能力相关结论：爬坡能力方面，倒立摆驱动模式与重摆驱动模式相同，且爬坡能力均随质心-球心距离的增大而增大。为了消除指标量纲的影响，进而对BYQ-GS型球形机器人样机不同摆长情况下的爬坡能力变化规律进行直观分析，基于式(13)对式(28)进行归一化处理，即重摆驱动模式与倒立摆驱动模式下的球形机器人爬坡能力ANorm(L)能够通过(29)进行表示

ANorm(L)=Norm[1/A(L)]

(29)

2.2.2 指标2：转向能力(统计指标：运动路径与初始-目标位置连线的最大距离Dmax)

在场景3中对不同摆长L与坡面角度γ进行组合，2种不同模式下运动路径与初始-目标位置连线的最大距离Dmax1与Dmax2的变化趋势,如图16所示(黑色符号为实验数据)。

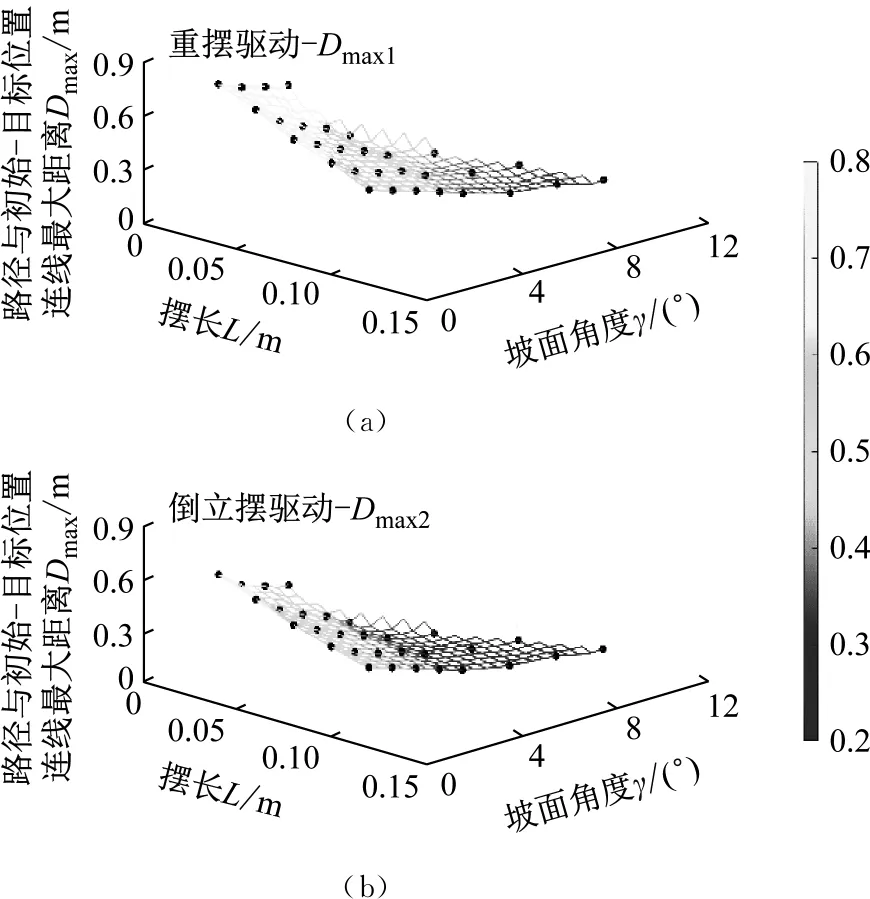
图16 场景3情况下Dmax的变化趋势图

当2种驱动模式的摆长L与坡面角度γ均保持一致时，0.061 m≤Dmax1≤Dmax2≤0.219 m，即转向能力方面倒立摆驱动模式与重摆驱动模式相比具有优势。

对图16所示实验数据进行公式化拟合，式(30)为运动路径与初始-目标位置连线的最大距离Dmax、摆长L与坡面角度γ的数学模型Dmaxi=B(i)(L,γ)的拟合结果。根据式(14)可得B(1)(L,γ)与B(2)(L,γ)对实验数据的拟合精度分别为0.007 4 m和0.008 2 m，该拟合精度不影响实验数据的趋势判断。

B(1)=-224.59L3+0.01γ3+85.44L2+0.01γ2-

14.92L-0.03γ+1.85L2γ-0.02Lγ2-

0.05Lγ+1.37,

B(2)=-156.89L3-0.01γ3+61.45L2+0.01γ2-

11.72L-0.08γ+0.22L2γ-0.02Lγ2+

0.45Lγ+1.19

(30)

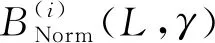
(31)

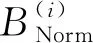
2.3 能耗水平分析

能耗水平评价指标为2种驱动模式下驱动电机在每个采样周期平均输出的功率Pi，对其变化情况进行分析，运用最小二乘法对实验数据进行公式化拟合(待定系数小数位为2)，建立其数学模型，并根据式(14)计算数学模型的拟合精度。

场景1：不同摆长L与期望速度vd进行组合，2种不同模式下驱动电机在每个采样周期平均输出功率P1与P2的变化趋势,如图17所示(黑色符号为实验数据)。

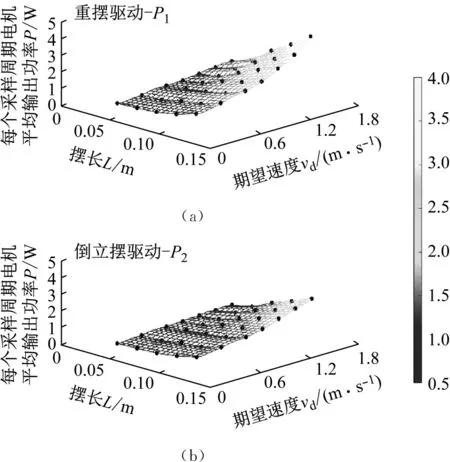
图17 场景1情况下P的变化趋势图

当2种驱动模式摆长L与期望速度vd均保持一致时，0.103 W≤P1-P2≤1.452 W，即能耗水平方面倒立摆驱动模式与重摆驱动模式相比具有优势。

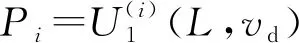
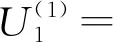
9.03Lvd+1.15,

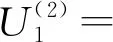
0.29Lvd+0.95

(32)

场景2：不同摆长L与坡面角度γ进行组合，2种不同模式下驱动电机在每个采样周期平均输出功率P1与P2的变化趋势,如图18所示(黑色符号为实验数据)。

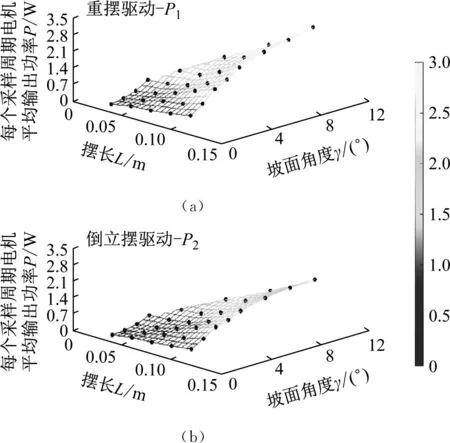
图18 场景2情况下P的变化趋势图

当2种驱动模式下球形机器人摆长L与坡面角度γ保持一致时，0.052 W≤P1-P2≤0.936 W，即能耗水平方面倒立摆驱动模式与重摆驱动模式相比具有优势。

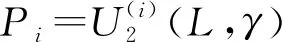
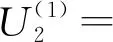
23.04L+0.20γ+51.62L2γ-0.72Lγ2-

3.88Lγ-0.31,

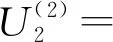
15.41L+0.12γ+41.61L2γ-0.59Lγ2-

3.10Lγ-0.15

(33)

场景3：不同摆长L与坡面角度γ进行组合，2种不同模式下驱动电机在每个采样周期平均输出功率P1与P2的变化趋势,如图19所示(黑色符号为实验数据)。

当2种驱动模式下球形机器人摆长L与坡面角度γ保持一致时，0.035 W≤P1-P2≤1.482 W，即能耗水平方面倒立摆驱动模式与重摆驱动模式相比具有优势。

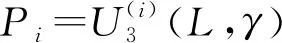
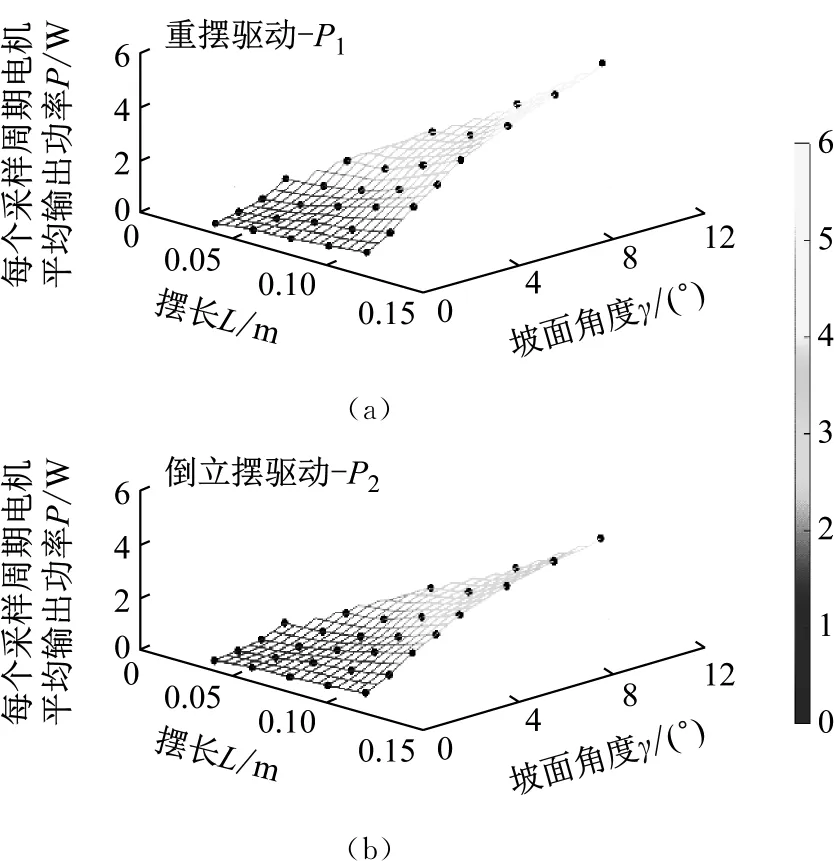
图19 场景3情况下P的变化趋势图

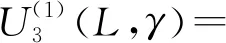
36.40L+0.30γ+74.53L2γ-0.92Lγ2-

5.61Lγ-0.63,

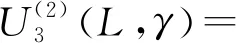
21.50L+0.16γ+64.14L2γ-0.84Lγ2-

4.23Lγ-0.27

(34)

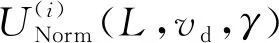
(35)

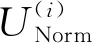
3 运动特性总结

根据2种不同驱动模式下质心径向变化的直线运动和全方位运动相关实验研究结果，针对控制性能、运动能力以及能耗水平3个方面，对质心径向可变球形机器人的运动特性进行总结。

3.1 质心径向可变球形机器人运动特性规律

以重摆驱动模式下的球形机器人运动为对比基准，从控制性能、运动能力以及能耗水平3个方面出发，将倒立摆驱动模式以及质心径向变化功能对球形机器人运动特性的影响规律总结如下：

控制性能方面，与重摆驱动模式相比，倒立摆驱动模式在控制系统超调量与响应速度方面具有优势，在控制系统收敛速度与稳定性方面具有劣势。

运动能力方面，倒立摆驱动模式与重摆驱动模式下球形机器人爬坡能力相同，且爬坡能力均随质心-球心距离的增大而增强。与重摆驱动模式相比，倒立摆驱动模式在转向能力方面具有优势。

能耗水平方面，与重摆驱动模式相比，倒立摆驱动模式在能耗水平方面具有优势。

根据上述影响规律，当面对高运动灵活性或长续航的应用需求时，可选择倒立摆驱动模式下的球形机器人；当面对高稳定性的应用需求时，可选择重摆驱动模式下的球形机器人。

3.2 运动特性需求与质心径向位置的关联模型

以运动特性分析部分中对BYQ-GS型球形机器人样机在控制性能、运动能力与能耗水平方面构建的多项指标数学模型为基础，在坡面角度、运动速度以及最优摆长方面对BYQ-GS型球形机器人样机与实际使用的球形机器人进行一一映射，构建球形机器人运动特性需求与质心径向位置的关联模型，使其普遍适用于质心径向可变球形机器人。该模型可根据球形机器人对运动特性的不同需求，对控制性能、运动能力以及能耗水平进行综合考虑。

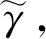
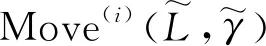
(36)

将重摆的最优摆长确定问题转换为如式(37)所示的最优化问题

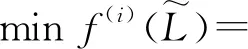
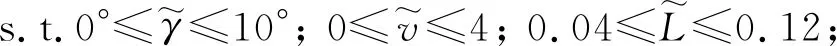
(37)

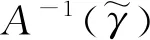
(38)

式中，Lmax为球形机器人能够实现的最大摆长。

任务准备阶段，质心径向可变球形机器人首先根据2种驱动模式的运动特性规律与任务实际需求对驱动模式进行选择，然后根据任务对运动特性的需求，以及需要面对的坡度γ与需要具备的运动速度v，基于式(37)与式(38)对最优摆长L进行确定与调节，使球形机器人面对非结构化任务环境的实用性大大提升。

4 运动特性分析结果的实验验证

以BYQ-GS型球形机器人样机作为实验平台，运用HSMC实现球形机器人运动控制，以传统重摆驱动模式下摆长L保持0.12 m恒定的运动效果作为对比，对根据运动特性需求进行驱动模式与最优摆长选取后的运动效果展开实验验证。实验环境为室外田径跑道。

实验模拟非结构化环境下的2种不同任务需求：任务1需要任务执行过程中能耗表现最优，任务2需要控制超调量较小，同时保证控制性能最优前提下兼顾能耗水平表现。根据上述任务需求以及式(37)中n1,n2,n3与运动能力、控制性能、能耗水平之间的对应关系，将实验1的运动能力权重参数n1设置为0.1，控制性能权重参数n2设置为0.2，能耗水平权重参数n3设置为0.7；将实验2的运动能力权重参数n1设置为0.1，控制性能权重参数n2设置为0.6，能耗水平权重参数n3设置为0.3。坡面角度γ设置为0°，期望速度vd设置为1 m/s。

根据3.1节质心径向可变球形机器人运动特性规律，实验1与实验2中BYQ-GS型球形机器人样机均选取倒立摆驱动模式，即式(37)中的驱动模式参数i设置为2，运用MATLAB软件中的fmincon函数对式(37)所示的最优化问题求解，可得实验1的摆长最优解为L=0.053 m，实验2的摆长最优解为L=0.098 m[18]。

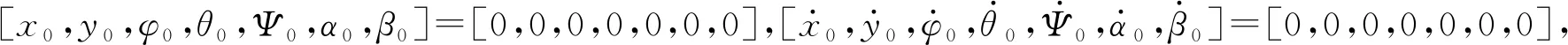
表3 面向实验1需求的实验数据统计指标对比

表4 面向实验2需求的实验数据统计指标对比

实验1任务需求为能耗表现最优，因此对驱动电机在每个采样周期平均输出功率P展开对比。根据表3所示实验数据统计指标，与重摆驱动模式下摆长L=0.12 m相比，当摆长L=0.053 m且球形机器人处于重摆驱动模式时指标P下降幅度为54.67%，当摆长L=0.053 m且球形机器人处于倒立摆驱动模式时指标P下降幅度为67.03%。上述结果表明与重摆驱动模式下摆长L=0.12 m相比，当球形机器人处于倒立摆驱动模式且摆长L=0.053 m时，能耗表现得到大幅度提升。

实验2任务需求为控制超调量较小，同时保证控制性能最优前提下兼顾能耗水平表现，因此对收敛时间tr、运动未收敛时位置误差的最大绝对值|ex|max与|eα|max、运动未收敛时位置误差的均方根误差ex-rmse与eα-rmse、运动过程中最大力矩产生时间tτ-max4类控制性能指标，以及驱动电机在每个采样周期平均输出功率P展开对比。根据表4所示实验数据统计指标，与重摆驱动模式下摆长L=0.12 m相比，当摆长L=0.098 m且球形机器人处于重摆驱动模式时4类控制性能指标平均提升幅度为40.75%，同时指标P下降幅度为19.35%；当摆长L=0.098 m且球形机器人处于倒立摆驱动模式时4类控制性能指标平均提升幅度为40.60%，同时指标P下降幅度为40.28%。上述结果表明与重摆驱动模式下摆长L=0.12 m相比，当球形机器人处于倒立摆驱动模式且摆长L=0.098 m时，控制性能出现下降但是能耗表现得到了提升。

上述2组实验结果表明，运用质心径向可变球形机器人运动特性规律以及球形机器人运动特性需求与质心径向位置的关联模型，可对球形机器人的驱动模式与最优摆长L进行选择与确定。

5 结 论

针对质心径向可变能力使球形机器人具备的倒立摆驱动模式以及质心的径向变化功能，将传统球形机器人具备的重摆驱动模式作为对比对象，根据非结构化环境下的任务特点开展了球形机器人在不同驱动模式、不同运动速度以及不同坡面角度情况下的运动实验，根据实验结果，基于控制系统的收敛速度、超调量、稳定性与响应速度4项控制性能指标、爬坡能力与转向能力2项运动能力指标以及能耗水平指标，对2种不同驱动模式下球形机器人在控制性能、运动能力以及能耗水平进行了分析，得出了以下结论：

(1) 总结了倒立摆驱动模式对球形机器人运动特性的影响规律，明确了与重摆驱动模式相比，倒立摆驱动模式具备的优势与劣势。

(2) 构建了球形机器人运动特性需求与质心径向位置的关联模型，为球形机器人在面对非结构化环境不同任务需求时质心径向位置的合理选取提供依据。

上述结论解决了倒立摆驱动与质心径向变化对摆式偏心力矩驱动机制球形机器人的运动影响不明确问题，对质心径向可变球形机器人在非结构化环境中实现多样化任务执行能力的提升有重要的理论意义和指导价值。