不同流场下含内流立管涡激振动响应特性及Coriolis力效应研究

李星辉， 袁昱超， 薛鸿祥， 唐文勇

(1.上海交通大学 海洋工程国家重点实验室，上海 200240;2.上海交通大学 船舶海洋与建筑工程学院，上海 200240)

海洋立管是海洋油气集输的重要部件。顶部张紧式(顶张式)立管是海洋开发中常用的立管类型之一，其底部与海底井口相连，顶部与平台张力系统连接，如图1所示。顶张力使立管保持垂直状态，避免其在外力作用下失稳。对于细长结构物而言，海洋来流会在结构两侧产生周期性脱落的漩涡，产生涡激振动(vortex-induced vibration，VIV)，进而诱发疲劳损伤甚至结构破坏。立管的涡激振动问题得到了国内外学者的持续关注，已有大量相关的试验研究和数值模拟。数值模拟大体上可以分为频域和时域两类方法。频域方法较为便捷，适合分析简单的线性动力学问题。时域方法应用更为广泛，适合分析复杂的非线性动力学问题。常用的立管的时域分析模型有计算流体动力学(computational fluid dynamics，CFD)模型、尾流振子模型和流体力分解模型等。CFD方法较为精确，但计算成本高，方法较为复杂，更加适合机理性探究。尾流振子法可以得到和试验数据较为接近的结果，但需要调整较多的经验参数[1]。相比之下，流体力分解法更为简便，且可以准确预报立管在多种外流场和时变激励下的涡激振动响应。本文主要采用流体力分解模型进行立管涡激振动响应的时域模拟。

当海洋平台正常工作时，立管内部充满以一定速度提升的油气等介质，内部流动的介质会对立管结构产生内部作用力。柳博瀚等[2]的研究表明内流通过增加轴向动力和改变弹性管道局部曲率的方式影响管道的振动频率。因此研究立管的动力响应时，内流的影响不容忽视。含内流立管的涡激振动响应是更为复杂的非线性动力学问题。Guo等[3]开展了含内流立管涡激振动的试验研究，试验结果表明内流会降低立管涡激振动的响应频率，增大响应振幅，随后学者的数值研究大多也都验证了这一规律。根据侧重点的不同，立管内流效应的相关研究大致可分为3类：内流本身的属性、立管的布置形式和外部激励等。内流本身的属性包括内流流速、密度、流体性质等。对于内外流同时作用下的顶张式立管，当内流流速处于亚临界区时，立管仍然呈现出周期性的涡激振动；当内流流速处于超临界区时，立管的响应呈现混沌、分叉等新的特性[4]。Meng等[5-6]研究了立管涡激振动响应频率和振幅随内流速度和密度的变化规律。刘晓强等[7]发现黏性内流对立管动力特性和响应峰值都有所影响，但在实际工程中的影响有限。马天麒等[8]将内流的状态从单相拓展到多相，研究了气液两相内流的效应。立管的布置形式有顶张式、悬臂式、悬链线和缓波形等。刘震等[9-10]研究了内流对悬链线立管和缓波形立管动力特性的影响。Liu等[11-12]分别研究了悬臂式立管和悬链线立管在内流影响下的涡激振动响应特征。立管的外部激励主要来源于顶部浮式平台的运动。吴天昊等[13-14]分别通过试验和数值方法研究了立管在内流与平台运动联合作用下的动力响应特征。此外，内流的存在可能会减少立管的疲劳寿命[15-16]，因此在工程实际中内流的影响不容忽视。

尽管含内流立管的涡激振动问题已有一定程度的研究，但目前大多数相关研究的外部流场为均匀流。而真实的立管所处海洋环境中的外部流场更加接近剪切流的形式，剪切流下立管的涡激振动呈现更为复杂的多频响应特征。从机理层面分析，内流的效应体现为惯性力、离心力和科氏力三方面。惯性力项和离心力项中，位移分别仅对时间或空间求偏导，而科氏力项中位移同时对两者求偏导，导致科氏力的效应更为复杂。为进一步分析内流对立管涡激振动的影响，本文分别研究了含内流顶张式立管在均匀流和剪切流作用下的涡激振动响应特性，并重点分析了内流影响机理中相对复杂的科氏力作用。

1 含内流立管涡激振动时域模型

本文采用Cartesian坐标系统来描述立管模型，其中x轴方向为来流(顺流)方向，y轴方向垂直于来流(横流)方向，z轴方向竖直向上。典型的含内流立管涡激振动模型示意图,如图1所示。

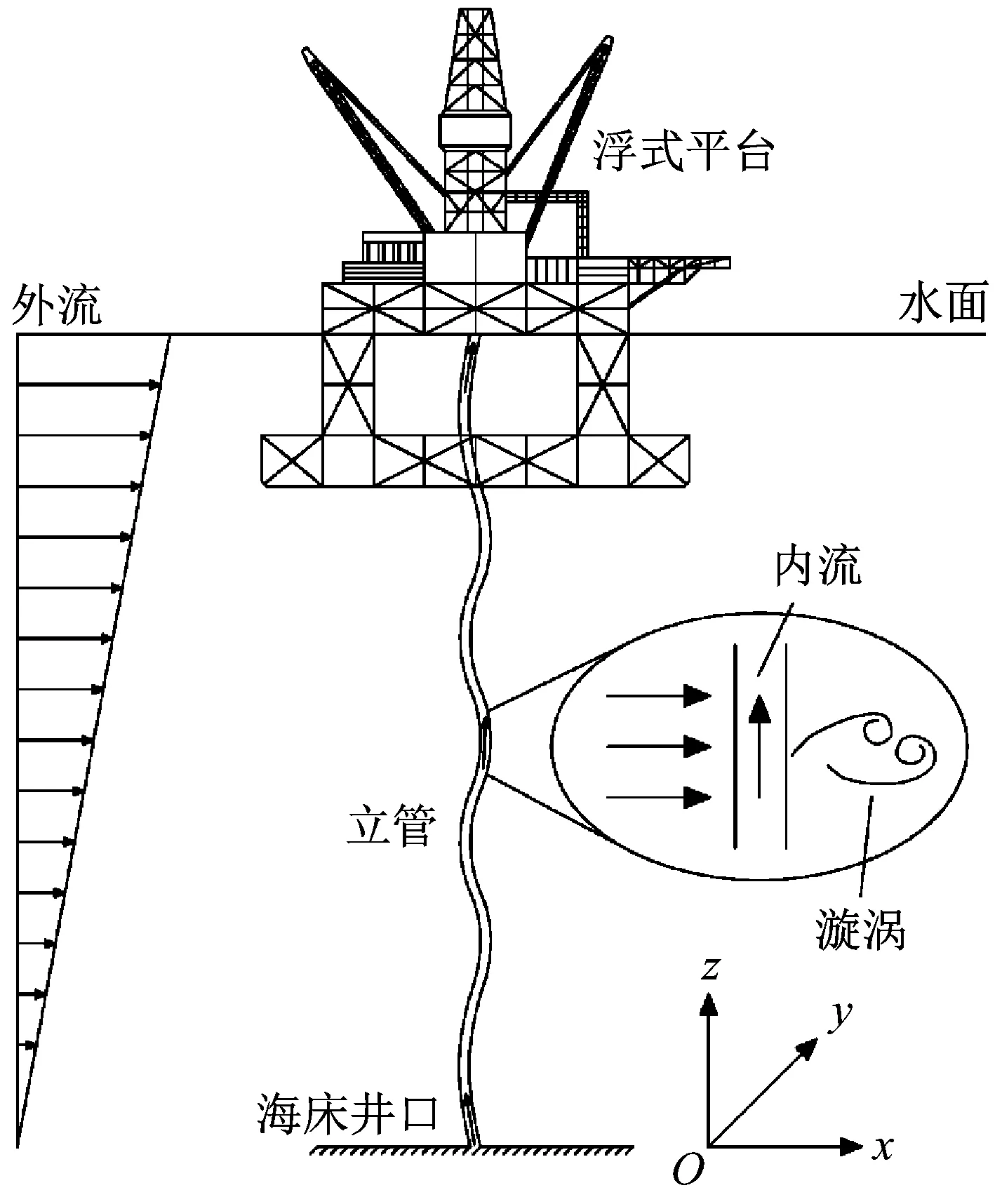
图1 浮式平台-立管-海床系统示意图

1.1 涡激振动流体力载荷

流体力分解模型将涡激振动流体力分解为与速度同相位的FV和与加速度同相位的FM

(1)

式中:CV为涡激振动激励力系数;ACF和fCF分别为横流方向涡激振动的振幅和频率;ρf为外流密度;D为立管外径;V为外流流速;Ca为附加质量系数，本文的附加质量系数设为1.0。

CV的值可以从Gopalkrishnan等[17]通过试验绘制的涡激振动激励力系数云图中得到，如图2所示。一组涡激振动频率和振幅对应云图中的一个数值，正的数值为激励力系数CV，负的数值转化为水动力阻尼系数cf。当响应频率或振幅超过云图范围时，采用Venugopal[18]的阻尼模型来计算水动力阻尼系数cf。

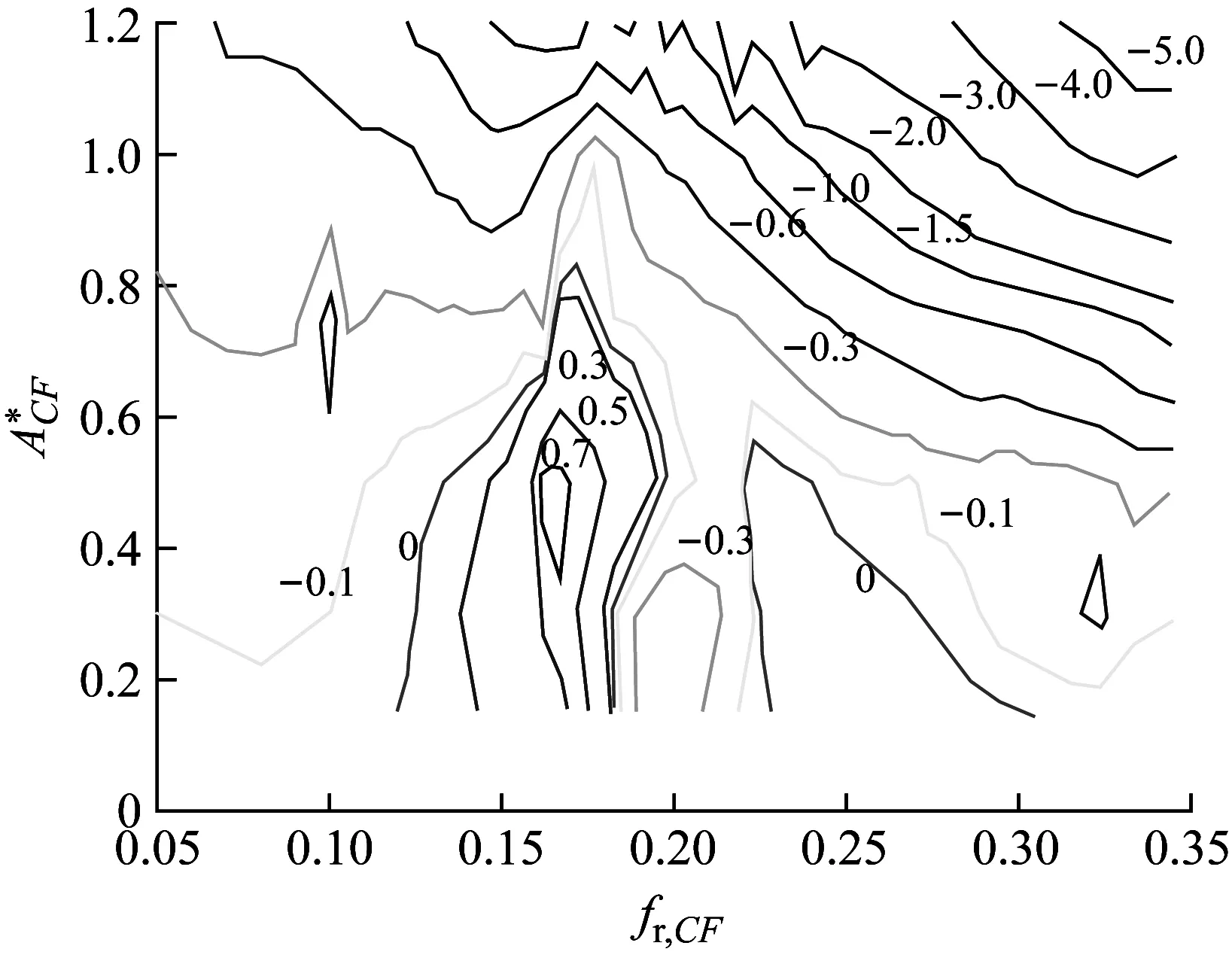
图2 涡激振动激励力系数云图

1.2 含内流立管涡激振动微分方程

不考虑重力、阻尼力和张力等外力时，含内流管道的运动方程[19]为

(2)

式中:m为立管单位长度的质量;mi为单位长度内流的质量;Ui为内部流体的流速;E和I分别为立管的杨氏模量和截面惯性矩。

含内流立管的完整运动方程为

(3)

式中:T为立管的有效张力;c为立管的阻尼。总阻尼c可分为水动力阻尼cf和结构阻尼cs=4πmfCFξ，其中ξ为结构阻尼比。

本文采用HHT(Hilber-Hughes-Taylor)方法求解式(3)来得到立管结构的涡激振动响应。HHT方法是一种改进的Newmark-β法，广泛应用于动力学问题的模拟[20]。式(4)定义了每一时间分析步内结构位置和速度的更新过程。

(4)

1.3 模型验证

本文采用的立管涡激振动时域模型已被验证过可准确预报立管在均匀流、剪切流和振荡流等多种外流场下的涡激振动响应，详见文献[21]。为验证本文对内流效应的准确模拟，与Duan等研究的数值模拟结果进行对比。Duan等的研究中的立管模型主要参数,如表1所示。外流取为流速1.6 m/s的均匀流。

表1 立管模型参数[6]

从不同内流流速下立管的固有频率和涡激振动均方根位移变化两方面进行对比，对比结果如图3和图4所示。

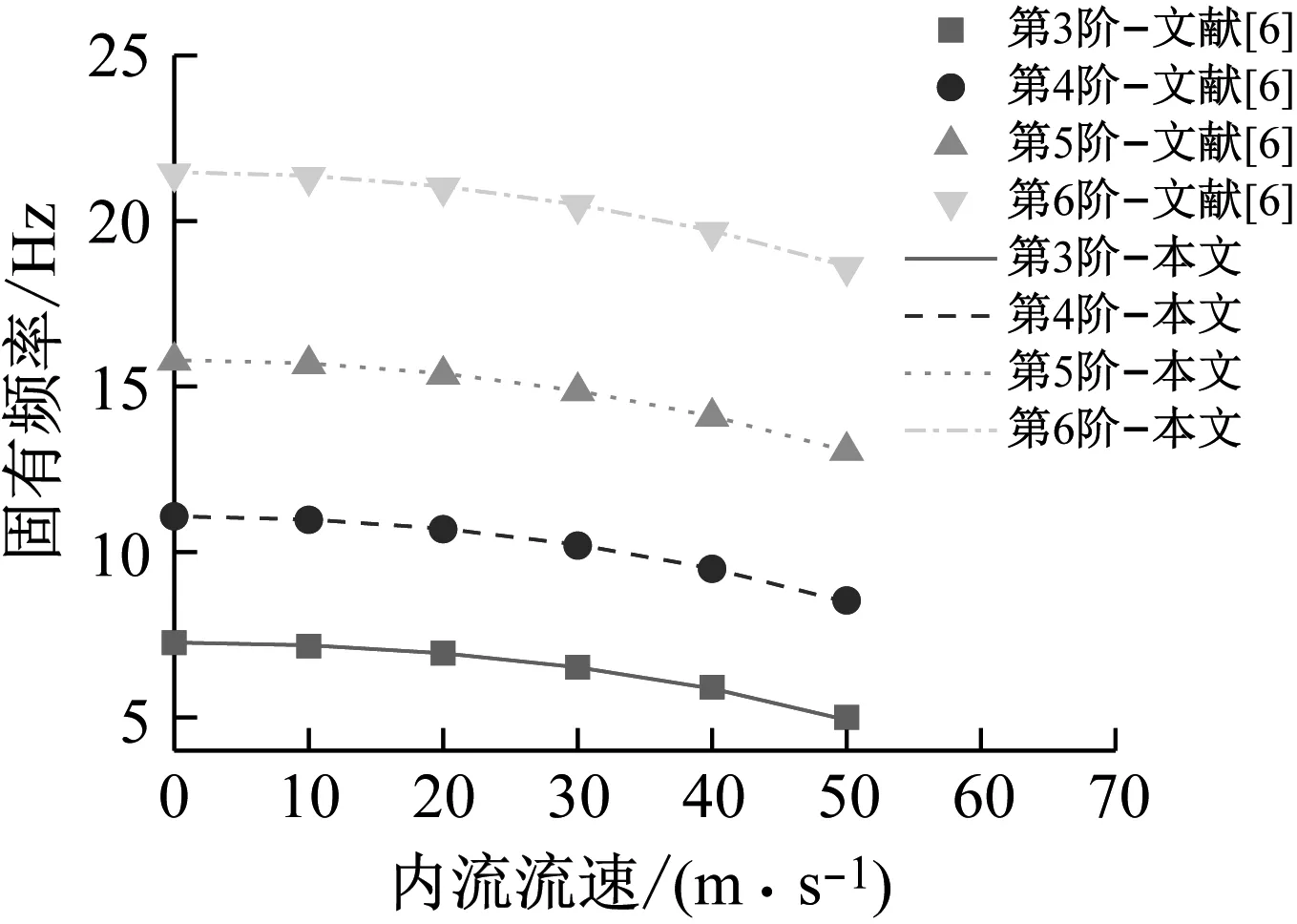
图3 不同内流流速下立管固有频率对比

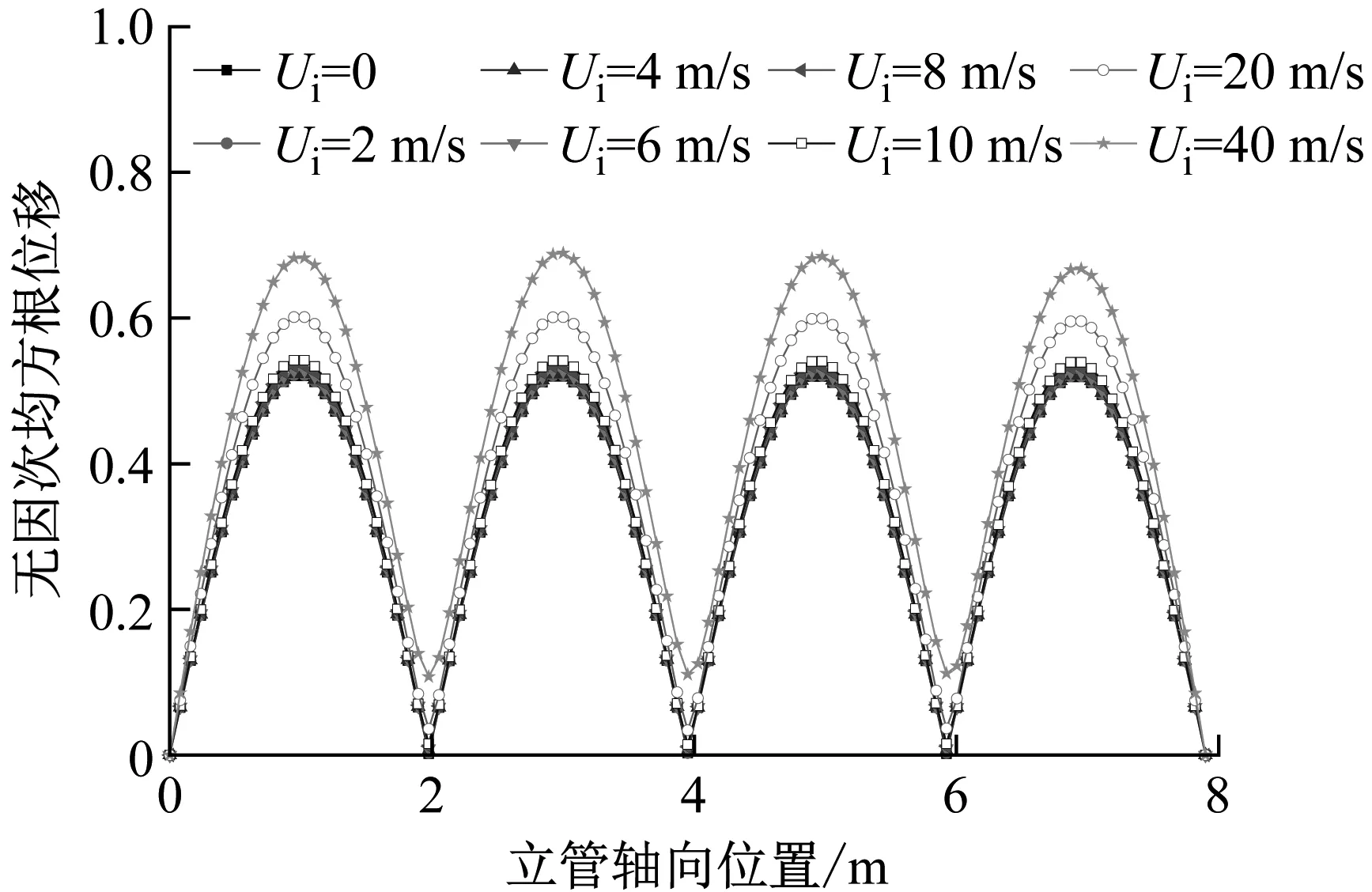
(a) 本文计算结果

随着内流流速的升高，立管的各阶固有频率都会有所降低。且当内流速度较低时，固有频率降低幅度不大；当内流速度较高时，固有频率显著降低。随着内流流速的升高，立管的均方根位移增大。且内流流速较低时，均方根位移增幅较小；当内流流速较高时，均方根位移增幅显著。

本文预报结果和Duan等的研究有较好的一致性，证明了本文模型对立管内流效应模拟的准确性。

2 均匀流下含内流立管涡激振动响应特征

1.3节中立管模型长细比较小(约为255)，而实际海洋立管的长细比通常在1 000以上，故有必要分析大长细比立管在均匀流下的涡激振动响应特征及内流效应。本节选取表2中的38 m长立管进行涡激振动时域模拟(长细比约1 407)，考虑了多个外流流速，并重点分析科氏力的效应。38 m立管模型取自文献[22]。

表2 大长细比立管参数

2.1 涡激振动响应特性(均匀流)

立管在不同内流流速下的固有频率变化,如图5所示。与图3相比，大长细比立管的固有频率本身较小，且随着内流流速升高，固有频率降低的程度相对更为缓和。固定外流为0.25 m/s均匀流，不同内流流速下立管无因次均方根位移曲线和立管位移时历快速傅里叶变换(fast Fourier transform，FFT)结果，分别如图6和图7所示。随着内流流速的升高，立管的均方根位移增大，响应频率降低，这与长细比较小的立管规律相同。下文重点分析不同外流及内流速度下科氏力的作用。

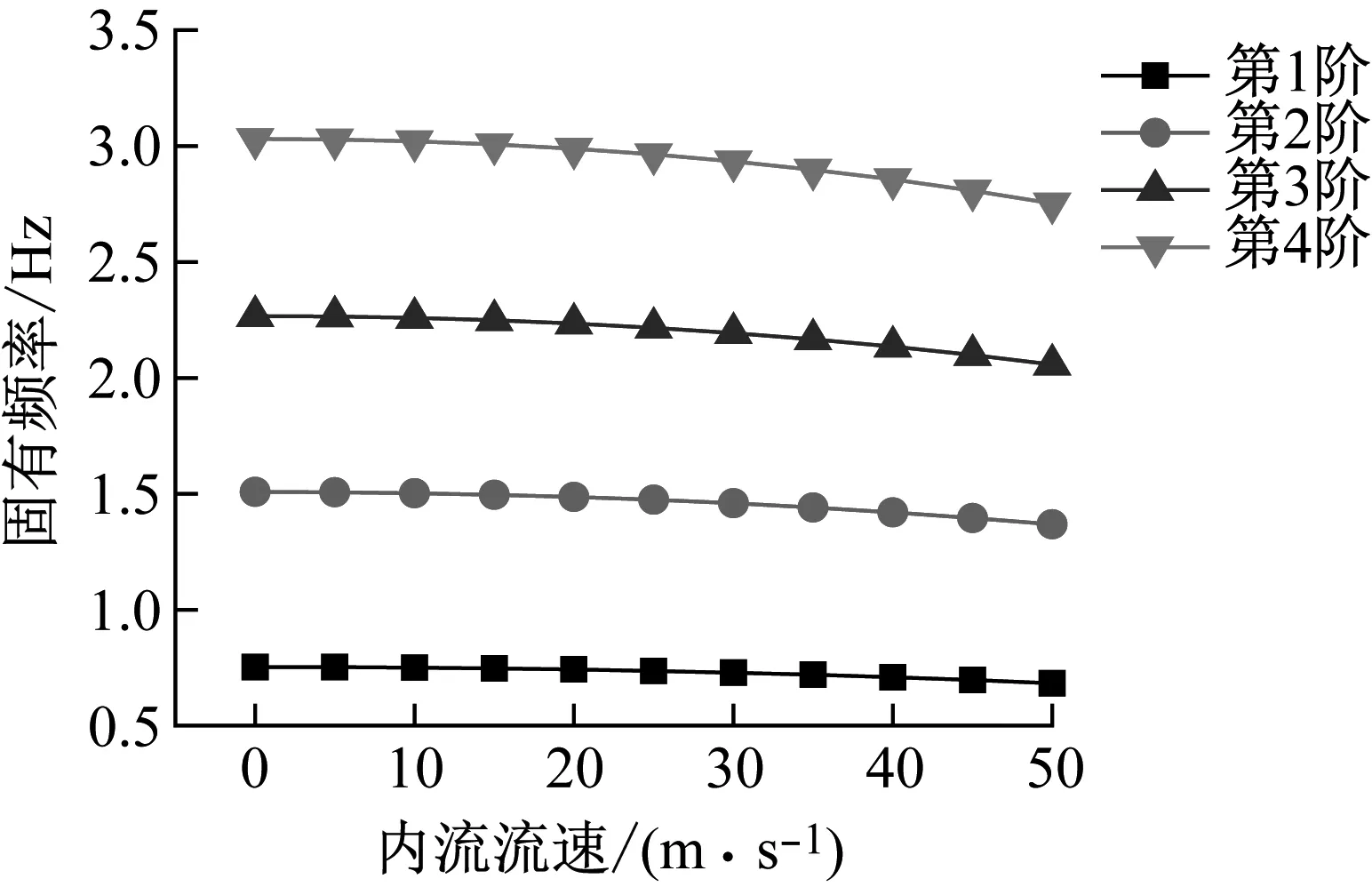
图5 不同内流流速下的立管固有频率

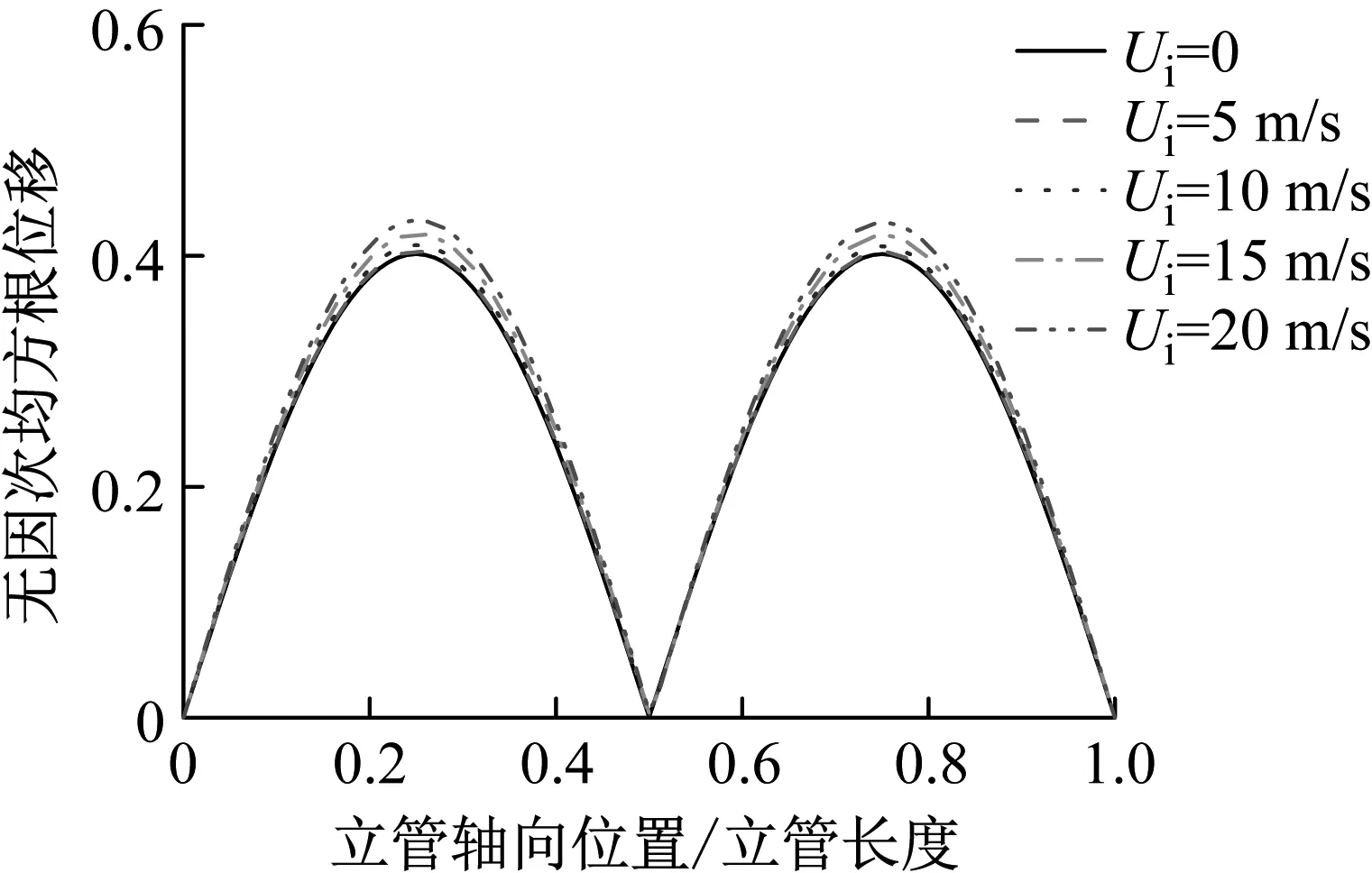
图6 不同内流流速下的立管均方根位移(0.25 m/s均匀流)

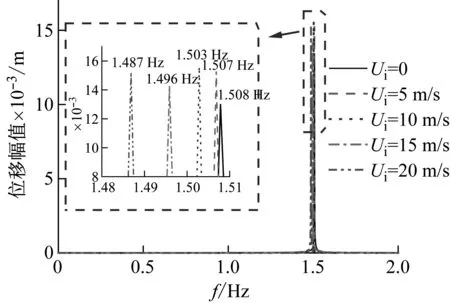
图7 不同内流流速下立管时历曲线FFT结果(0.25 m/s均匀流)

2.2 科氏力效应(均匀流)

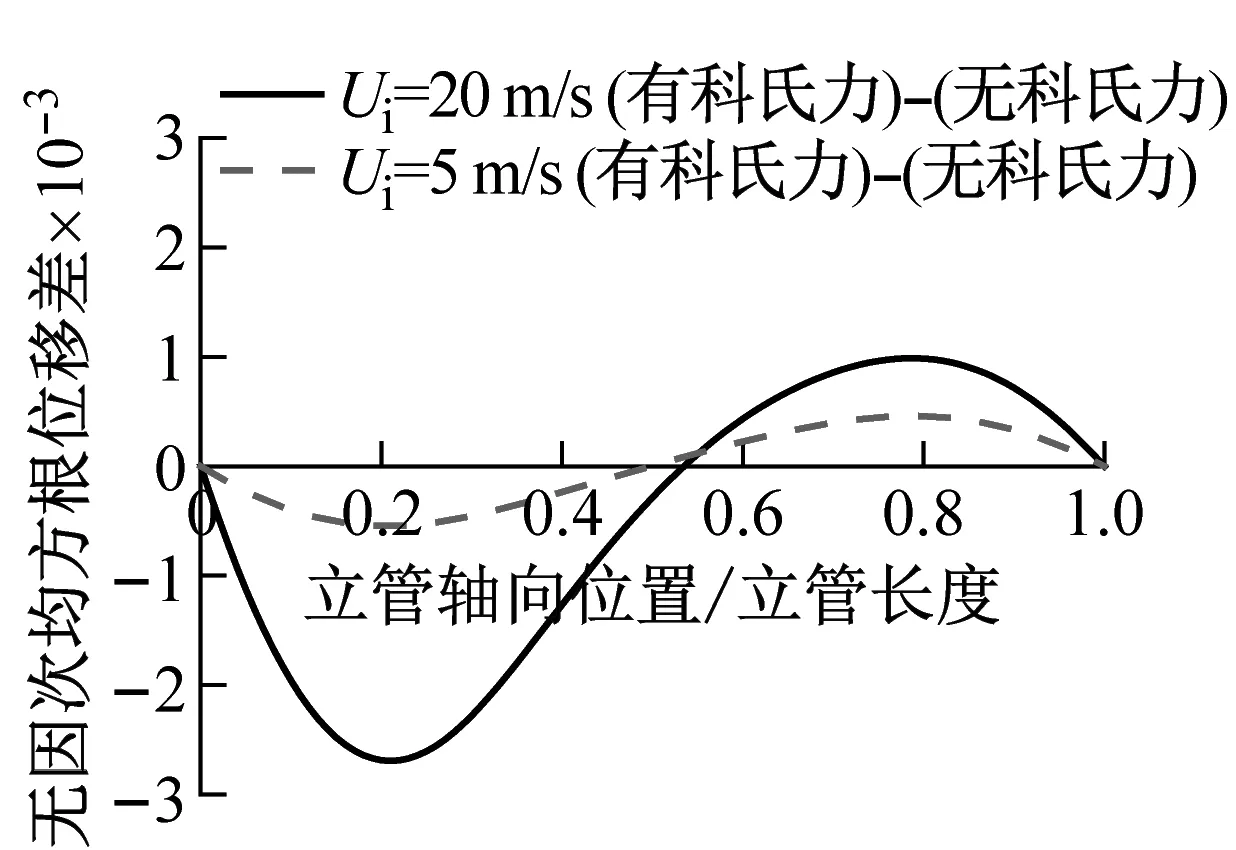
取0.15 m/s，0.25 m/s和0.4 m/s 3种均匀外流，固定内流流速为5 m/s和20 m/s，分别计算在立管数值模型中保留科氏力和去掉科氏力的涡激振动响应。其中0.4 m/s外流、20 m/s内流下立管均方根位移的结果对比，如图8所示。科氏力并不会引起均方根位移的显著改变，而是微调振型形状。为了更加清晰地表示科氏力的影响，将考虑与不考虑科氏力的无因次均方根位移曲线作差，如图9所示。

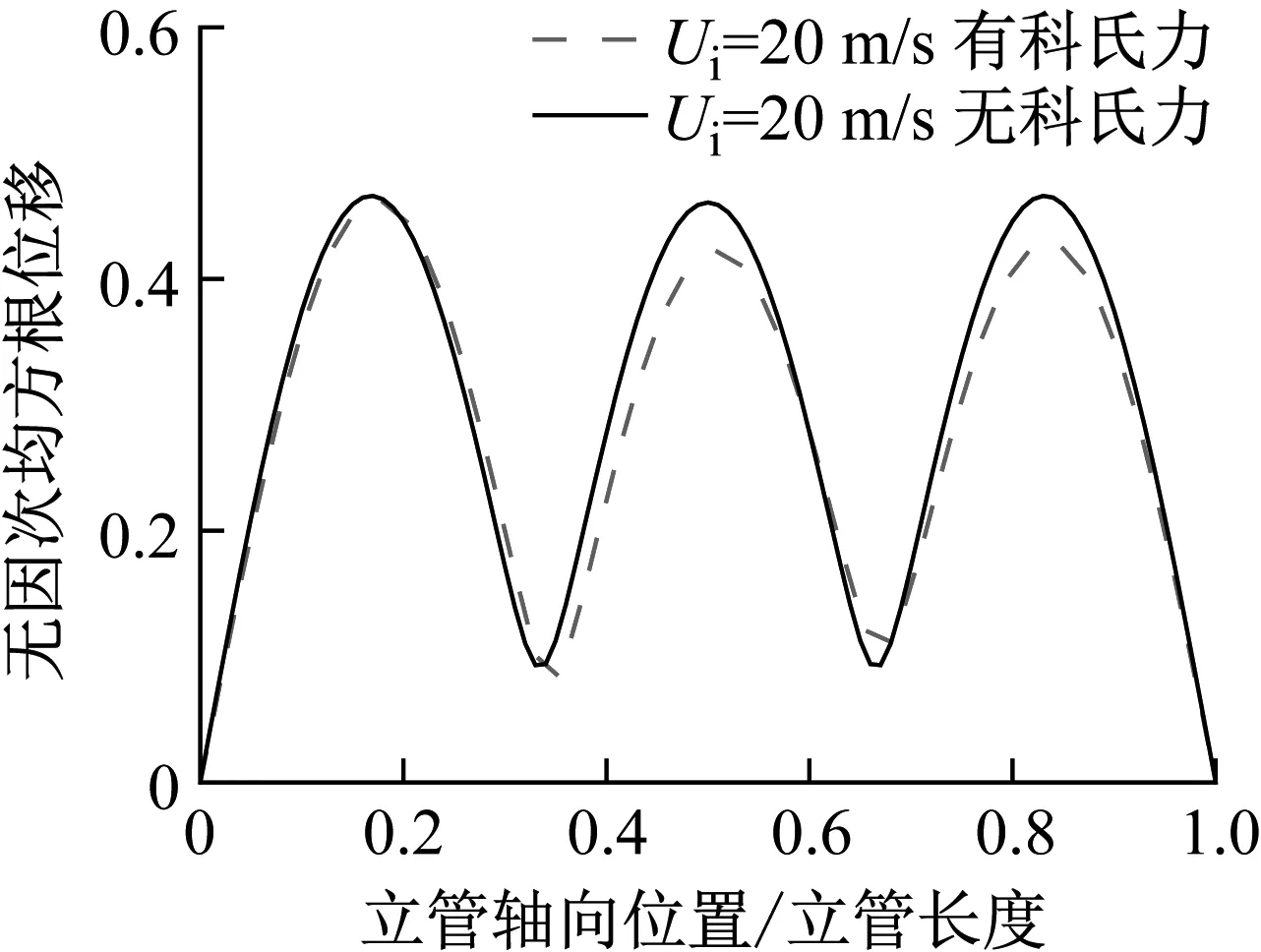
图8 有无科氏力情况下的立管均方根位移(20 m/s内流)

相同外流流速下，立管的内流流速越高，科氏力越大，均方根位移的改变量也相应增大。沿着立管的轴向，科氏力会在一些区域使得均方根位移有所升高，而在其余区域又使得均方根位移有所降低，且呈现出一定的规律性。在均方根位移振型的每一个“山峰”内，靠近立管底部区域的均方根位移降低，靠近立管顶部区域的均方根位移升高。

值得注意的是，当模态阶数较高(振型“山峰”数量较多)时，最靠近顶部的振型“山峰”内均方根位移升高的区域可能会很小甚至不存在，且从图9(b)可见内流流速越高，这一特性越明显。

(a) 0.15 m/s均匀外流

3 剪切流下含内流立管涡激振动响应特征

为分析剪切流下的内流效应，本章选取表2中的90 m长立管(模型取自文献[23])进行涡激振动时域模拟。外流取顶流速为0.6 m/s的剪切来流。

3.1 涡激振动响应特性(剪切流)

不同内流流速下立管的均方根位移和响应频率的变化图,分别如图10、图11所示。剪切流下立管的涡激振动不再是单频的，而是呈现出多频响应的特征，且外流确定时，不同内流流速下立管的主导响应频率都位于一定的锁定区间内，但各阶响应频率的大小和占比都会有所区别。当内流流速为0和30 m/s时，立管的均方根分别呈现出第12和第13阶的振型。这表明内流流速较高时，立管的主导模态振型会有所升高，这是固有频率降低导致的。

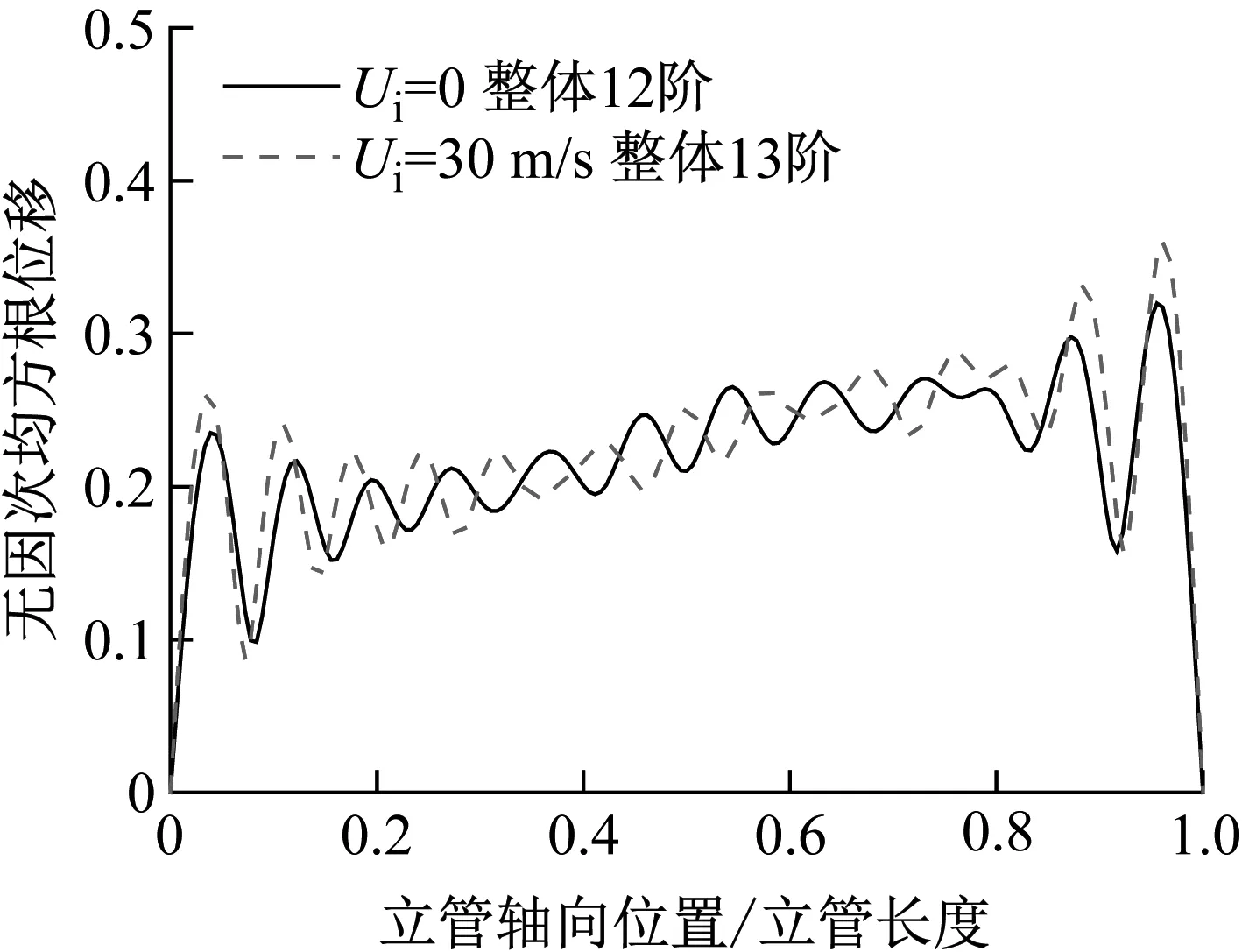
图10 不同内流流速下的立管均方根位移(0.6 m/s剪切流)

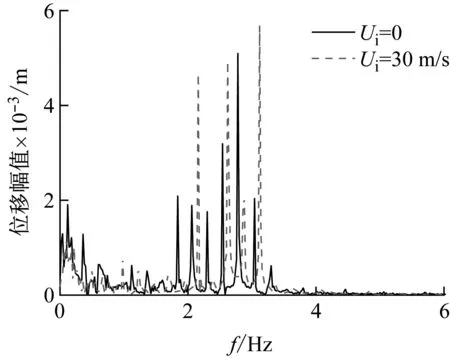
图11 不同内流流速下立管中点时历曲线FFT结果(0.6 m/s剪切流)

3.2 科氏力效应(剪切流)

为分析剪切流下的科氏力效应，同样分别计算保留科氏力和去掉科氏力的立管涡激振动响应结果。立管中点位移频响谱，如图12所示。科氏力并不会改变响应频率的大小，但会改变频谱图中的幅值分布情况。

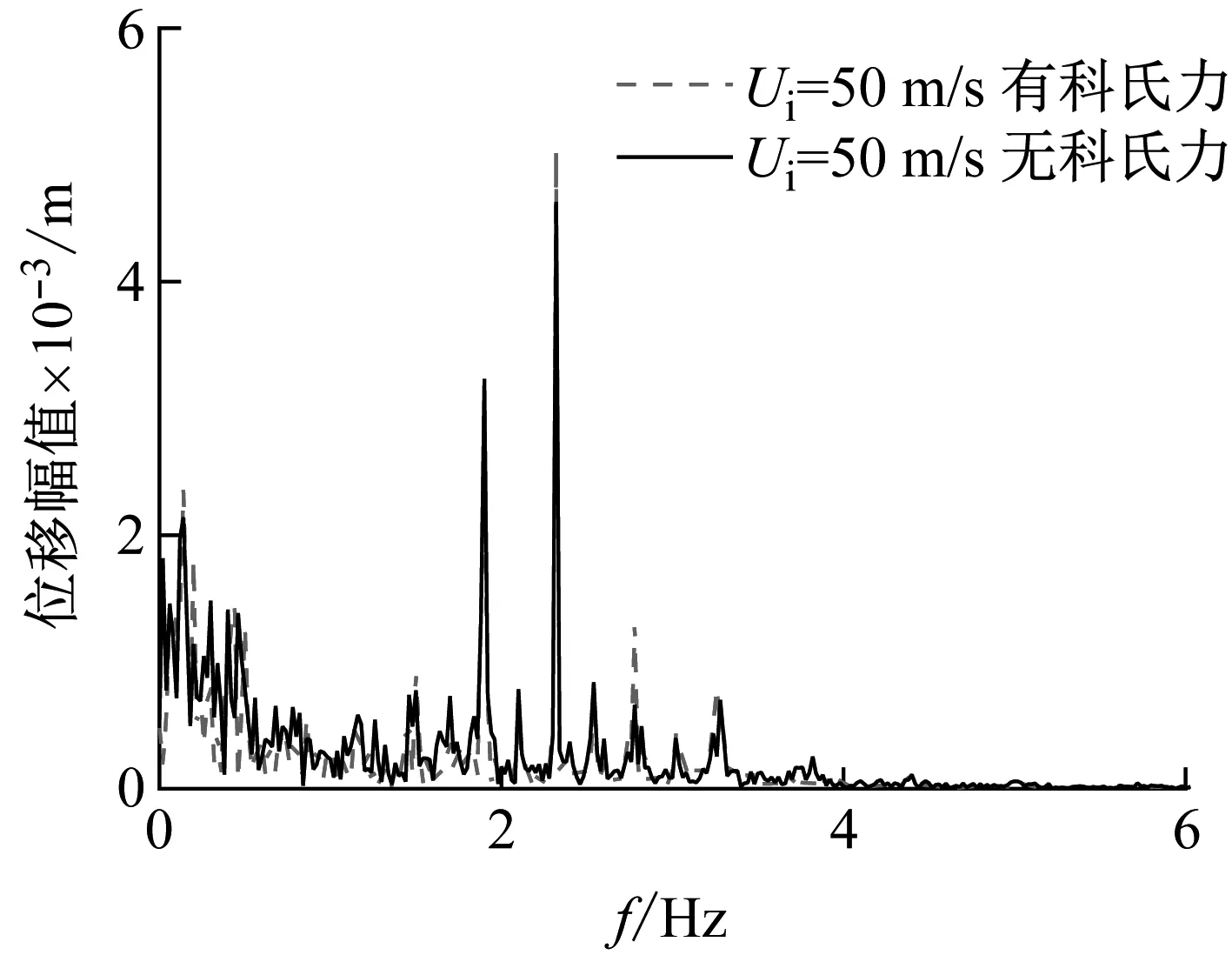
图12 有无科氏力情况下立管中点时历曲线FFT结果

考虑与不考虑科氏力情况下立管的均方根位移曲线,如图13所示。科氏力同样对响应振型产生了一定的调制作用，大体呈现出提高立管顶部区域均方根位移、降低立管中部区域均方根位移的规律。内流流速50 m/s下科氏力的效应更为明显，这是由于科氏力大小与内流速度相关，内流速度越大，科氏力效应越明显。

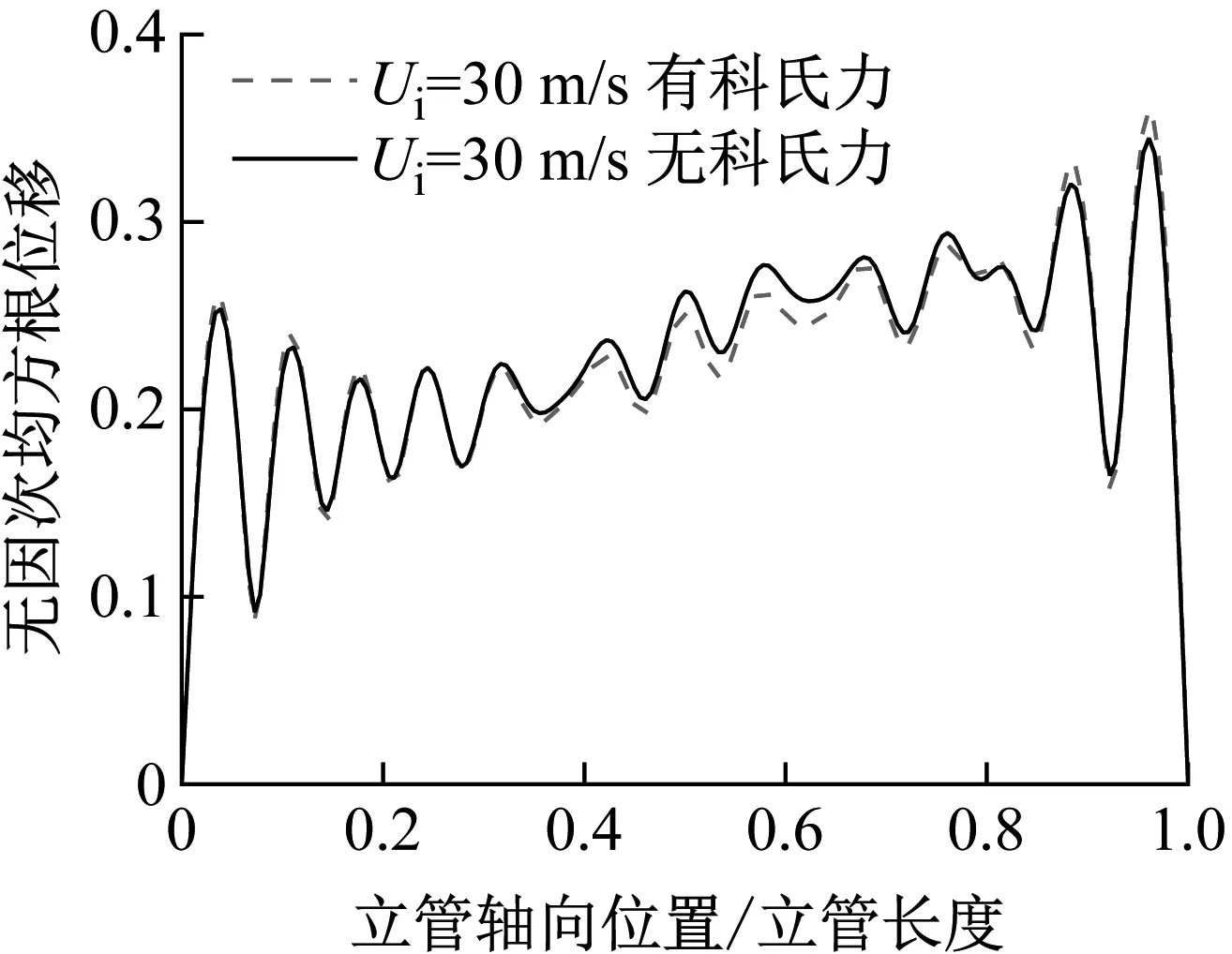
(a)

4 科氏力效应机理

第2章通过数值模拟，直观展示了内流对不同流场下立管涡激振动的影响。本章将从作用机理上分析内流效应，并重点关注较为复杂的科氏力作用。

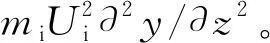
4.1 科氏力作用规律

从科氏力的基本表达式F=2mv×ω出发分析其效应。其中v和ω分别为内流的流速和立管的角速度矢量。图14中的实线和虚线分别为假定的立管某处位移和转角变化的时历曲线。将其分为A,B,C,D4个典型区域。

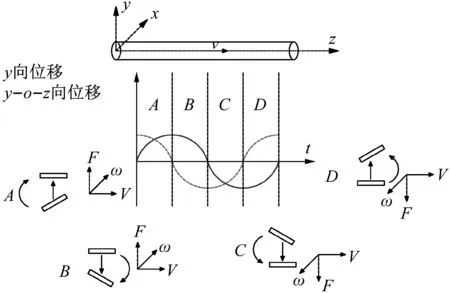
图14 科氏力作用机理示意图

区域A内立管位移增大，转角减小，可以判断出科氏力方向与立管位移同向，表明科氏力做正功。同理可知区域C内科氏力也做正功，区域B和D内科氏力做负功。不难得到：当立管单元位移变化趋势与转角变化趋势相反时，科氏力方向与位移方向相同，科氏力做正功；反之科氏力做负功。

4.1.1 均匀流工况

结合图9，由于均匀流下立管的响应是单频的，振型较为规则。振型中每个“山峰”的左半区域与图14中的B,D区域类似，科氏力做负功，故均方根位移降低；而振型中每个“山峰”的右半区域与图14中的A,C区域类似，科氏力做正功，故均方根位移升高。科氏力在靠近立管顶部的区域做正功，均方根位移应该会有所升高，但从图9(c)可见，立管顶部区域的均方根位移反而降低，这是由于存在边界效应。图15为某一时刻立管的振动形态，实线代表立管的振动速度方向，虚线代表科氏力方向。在顶部边界，科氏力做正功。在临近的左侧两个区域，尽管科氏力分别做负功和正功，但两个区域内科氏力的方向是相同的，使立管产生向下运动的趋势，如图15中的虚线所示，从而减小了顶部区域的振动幅值，最终体现为均方根位移的降低。由图9(b)可知，当内流流速为5 m/s时，立管顶部均方根位移有所升高，而当内流流速为20 m/s时，立管顶部均方根位移只有轻微升高，表明内流速度越高，这种边界效应越明显。

图15 科氏力的边界效应

4.1.2 剪切流工况

剪切流下立管的涡激振动响应频率较多，振动形态类似多个模态振型的叠加。此时科氏力的效应无法像均匀流工况一样直接从振型角度予以解释。故直接采用式(5)直接计算一段时间内科氏力在某一位置做功的大小。

(5)

一段时间内科氏力做功及立管的转角速度均方根值(root mean square，RMS)沿管长的分布情况,如图16所示。可见剪切流下，立管顶部的转角速度较大。此外剪切流下立管顶部区域的均方根位移较大，相应的振动速度较高，从而科氏力在顶部区域做功最大。且整体来看顶部区域内科氏力所做的正功大于负功，因此顶部区域的均方根位移会有所升高。Païdoussis的研究和本文的计算结果均表明，对于两端简支的管，科氏力对整个管做功为零。因此在立管的其余区域，科氏力整体做负功，均方根位移会有所降低。即剪切流下科氏力呈现出增大顶部区域位移、降低中部区域位移的效应，如图13所示。

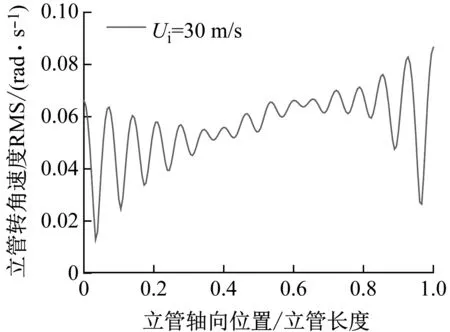
(a)

4.2 内流反向的影响

4.1节假定的内流流动方向是从底部到顶部，如图1所示。本节通过改变内流方向进一步探究科氏力效应机理。由式(2)可知，内流方向的变化只会影响科氏力。将内流反向即从顶部到底部流动，分别计算考虑与不考虑科氏力情况下立管的涡激振动响应。

0.15 m/s均匀外流下38 m立管保留和去除科氏力的均方根位移差曲线，如图17所示。与图9对比可知科氏力效应发生了以立管中点横截面为中心的对称变换。剪切外流下90 m立管保留和去除科氏力的均方根位移对比曲线，如图18所示。与图13对比可知科氏力的作用在内流反向时大体呈现出降低立管顶部均方根位移、提高立管中部均方根位移的规律。内流反向将导致科氏力同时反向，从而原本科氏力做正功的区域变为了科氏力做负功，反之亦然。因此科氏力对振型的调制规律也发生了改变。

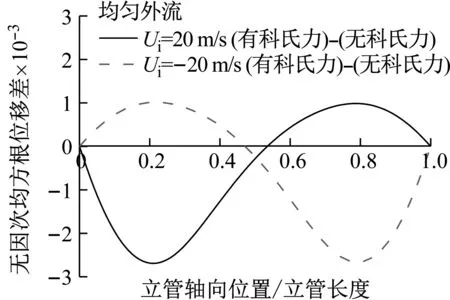
图17 有无科氏力情况下的立管均方根位移差值(内流反向)

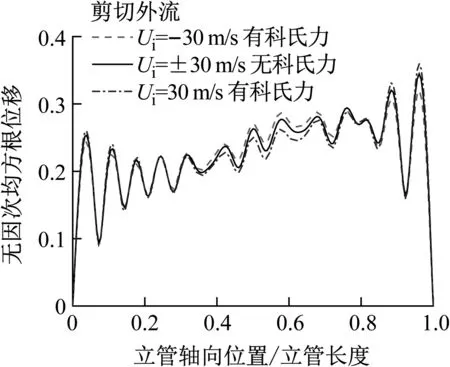
图18 有无科氏力情况下的立管均方根位移(内流反向)

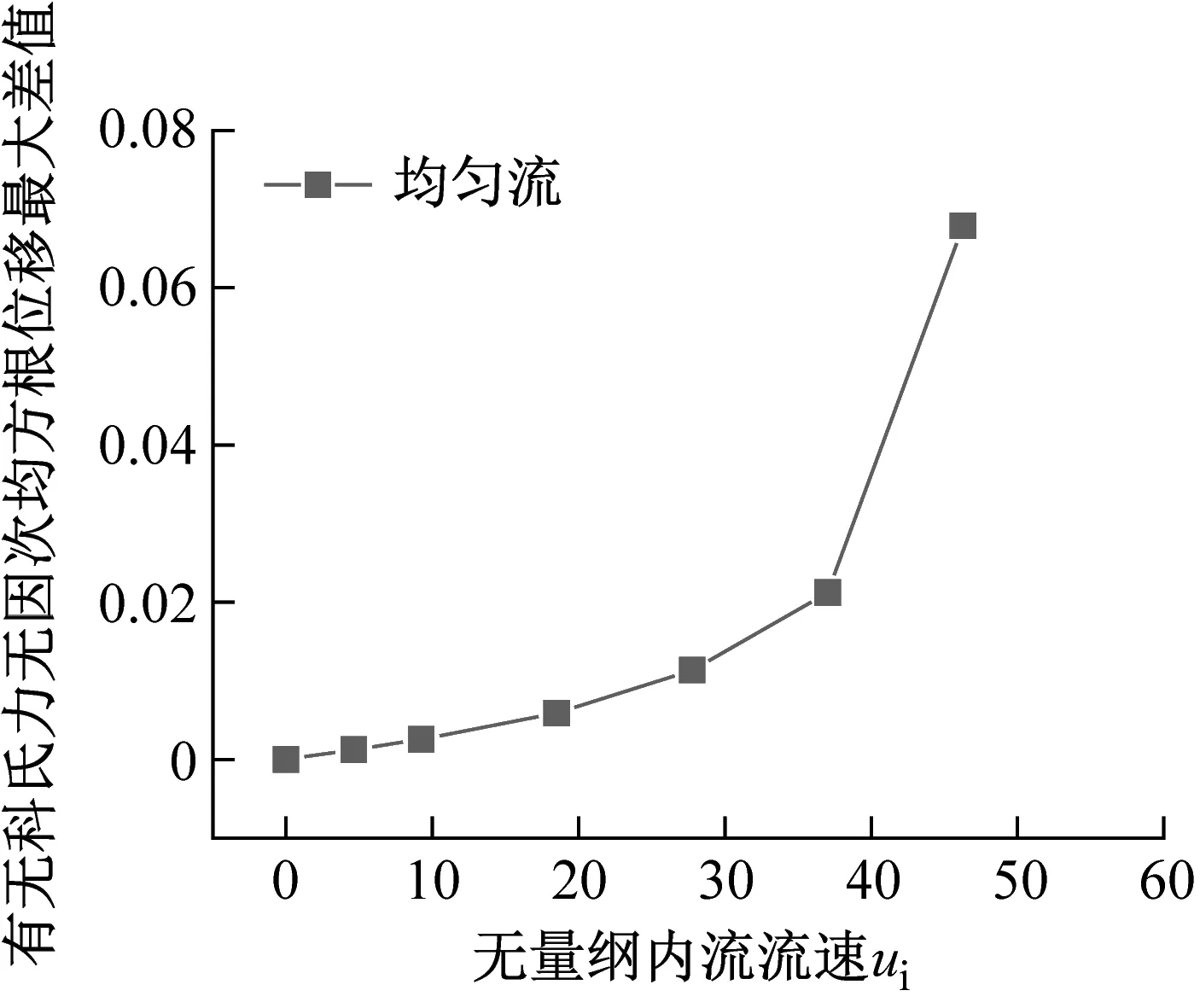
4.3 内流速度的影响

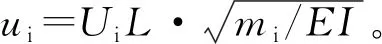
(a) 0.25 m/s均匀流

5 结 论

基于含内流立管的涡激振动响应时域预报模型，本文分别研究了均匀外流和剪切外流下内流对顶张式立管涡激振动响应特性的影响。从作用机理上重点分析了内流引起的复杂科氏力效应。得到的主要结论如下：

(1) 内流对立管涡激振动的影响体现在惯性力、科氏力和离心力三方面。惯性力会使立管单位长度质量增加；离心力会降低立管的有效张力；而科氏力会改变立管的振动形态，不会改变响应频率。

(2) 均匀外流下，随着内流流速的升高，立管响应频率降低，均方根位移增大；剪切外流下，立管呈现多频响应特征，主导频率位于一定的锁定区间，且随着内流流速的升高，主导模态阶数有上升趋势。

(3) 均匀流下，科氏力在每个振型“山峰”内左侧和右侧区域分别做负功和正功，并引起均方根位移减小和增大；剪切流下，科氏力使得立管顶部区域均方根位移增大，中部区域均方根位移减小。

(4) 内流流向改变不影响惯性力和离心力，仅影响科氏力。内流反向时，均匀流下，科氏力在每个振型“山峰”内的左侧和右侧区域分别做正功和负功，并引起均方根位移的增大和减小；剪切流下，科氏力使得立管顶部区域均方根位移减小，中部区域均方根位移增大。

(5) 内流流速越大，均匀外流和剪切外流下科氏力的效应都会更加明显。为准确预报立管的涡激振动，保证结构安全性，建议实际工程中考虑内流效应时应充分考虑科氏力的效应。

综上，本文分别从数值模拟和机理分析角度讨论了内流效应，研究结论有助于理解内流对海洋立管涡激振动的影响规律，并可为立管实际工程设计提供一定参考。

同时，本文还存在一定的局限和不足。工程实际中的内流并不是单相流，而是多相流的形式，建议今后的工作将内流效应扩展到多相内流效应。另外本文的研究对象为顶张式立管，科氏力对其他形式立管(悬链线立管、缓波形立管等)的效应有待进一步研究。