基于Woodbury+OpenMP的结构非线性地震反应并行分析方法

余丁浩， 李 钢

(大连理工大学 建设工程学部海岸和近海工程国家重点实验室， 辽宁 大连 116024)

随着工程结构逐渐向大型化和复杂化方向发展，基于传统变刚度法的结构非线性地震反应计算平台所需巨大计算耗时已越发难以满足工程建设需求，尽管目前计算机技术已获得了长足发展，但大型结构抗震分析所面临的效率瓶颈依然是制约结构工程发展的重要因素，如何在保证高精度计算模拟的同时有效提升结构分析效率始终是工程界重点关注问题。

利用计算机的多线程计算能力或搭建集群化计算环境通过并行方式进行结构非线性地震反应分析是提升计算效率的重要途径，从编程角度来看可将当前结构分析领域常用的并行计算模式分为两类：共享内存式和分布内存式。共享内存式是指多个计算线程共用一个数据存储空间，主要用于单机计算，如基于OpenMP的多核CPU(central processing unit)并行计算[1-2]，基于GPU的并行计算[3-11]等，具有维护和编程相对简便的优点；分布内存式主要利用计算机集群实现高性能计算，不同计算设备之间通过必要的数据通讯进行协调，此类并行计算通常采用消息传递的编程模式(message passing interface，MPI)实现，虽然其理论上可以实现超大规模问题的计算分析，但编程方式复杂、设备维护代价高，且不同计算设备之间无法避免的数据通讯导致计算效率存在瓶颈。在实际应用中，上述两种并行模式可以混合使用，以进一步降低分析耗时，例如何强等[12]通过对整个求解域进行剖分，将不同子域分配到不同计算设备上，并在单机上利用OpenMP进行线程级别并行加速，提出了基于MPI+OpenMP混合编程模式的并行计算方法。此外，为充分发挥不同并行计算模式的效能，众多学者有针对性的提出了多种便于并行实现的结构分析方法，如单元接单元方法[13-16]、区域分解法[17-21]等，其中单元接单元方法不需总装整体刚度矩阵和荷载向量，运算主要集中在单元层面，该方法通常与预处理共轭梯度法相结合，多用于共享内存式的并行计算；区域分解法采用分而治之的思想，将结构划分为不同的计算区域，其关键在于建立能够实现负载平衡的区域划分方式和界面方程求解方法，多用于分布式计算集群。

结构在地震作用下的非线性变形通常集中于局部区域，如部分梁柱端部、墙底等部位，已有研究表明，充分利用结构的局部非线性特征有助于大幅提升非线性地震反应分析效率，当前已发展出多种高效局部非线性分析方法，如拟力法[22-26]、数值子结构法[27-30]、多尺度类方法[31-32]、快速非线性分析法[33-34]等，这些方法多通过保持结构刚度矩阵恒定或缩减问题规模的方式避免结构大规模刚度矩阵实时更新及由此导致的计算效率降低。在现有的局部非线性分析方法中，基于Woodbury公式的结构非线性分析方法[35-37](简称Woodbury方法)因具有较好的数学理论基础和较广泛的适用性，近年来得到了越来越多的关注，此类方法将任意时刻的结构切向刚度改写为初始弹性刚度的低秩摄动形式，进而引入线性代数领域中的Woodbury公式求解结构切向位移反应，能够避免了大规模整体切向刚度的迭代更新，仅需对代表局部非线性行为的小规模矩阵进行实时更新和分解，可显著提升非线性问题计算效率。Deng等通过将结构切向刚度中局部时变元素单独取出，建立了以Woodbury公式为高效求解器的虚拟力分析法。近期Li等[38-40]以拟力法中的变形分解思想为出发点，通过对局部区域内进入塑性的材料进行应变分解，在单元层面构造非线性应变场函数，提出了隔离非线性有限元法基本理论，该方法采用Woodbury公式进行控制方程求解，且具有适用性广、通用性好等优点，能够实现一般结构的高效非线性地震反应分析。随后，众多学者围绕该方法的算法优化、计算应用等开展了系列研究[41-48]，进一步丰富了其理论体系。尽管Woodbury方法能够从算法理论层面解决传统非线性分析方法由于刚度矩阵时变导致的效率瓶颈，但现有研究均采用串行计算模式，并未充分利用计算硬件的并行加速能力，因而其高效性优势并未得到充分发掘。

本文将OpenMP并行计算模式引入到Woodbury方法中，提出了一种基于Woodbury+OpenMP的高效结构非线性地震反应分析方法。首先采用隔离非线性法构造结构切向刚度方程的摄动展开表达式及相应Woodbury求解公式，随后，分别针对Woodbury公式计算、单元状态确定、局部非线性系数矩阵更新这3个非线性迭代求解过程中主要计算步骤建立了基于OpenMP的并行优化策略，实现了该方法的全过程并行加速，最后，通过一个高层结构算例验证了本文方法的高效性和准确性。

1 Woodbury方法基本理论

本文采用隔离非线性法构造用于结构地震反应分析的Woodbury求解公式。使用图1所示结构对该方法中控制方程的基本推演过程进行说明，设在某个计算步下单元i进入非线性，图1给出了该单元中任一点材料的应力应变关系，其中σ和ε分别为当前的材料应力和应变，根据材料初始弹性模量Ee可将应变ε分解为弹性和非线性两部分，其中弹性应变ε′等于假设材料保持初始弹性状态时达到应力σ对应的应变(即ε′=σ/Ee)，非线性应变ε″等于总应变ε与弹性应变ε′的差(即ε″=ε-ε′)。进一步利用插值方法在单元层面构造材料非线性应变分布场函数，并结合虚功原理，即可建立增量形式的单元隔离非线性控制方程

(1)

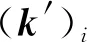
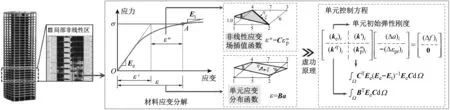
图1 隔离非线性法基本原理

(2)

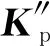
在任一迭代计算步中，将式(2)中的非线性自由度进行凝聚可得摄动式刚度方程式(3)。

(3)

式中:n为结构位移自由度数；m为当前计算步下结构的非线性自由度数，代表了结构非线性区域规模的大小。式(3)等号左边括号中表达式的计算结果与结构当前的切向刚度Kt等效，该表达式代表了切向刚度的低秩摄动。当结构局部非线性区域的规模较小时，非线性自由度数目m将远低于结构的位移自由度数数目n(即m≪n)，可利用式(4)对式(3)进行高效求解。

(4)

(5)

当结构规模较大时，虽然式(4)中整体刚度Ke的规模较大，但其为常数矩阵，可仅在分析前合成并进行一次分解，可见，Woodbury公式的使用可以避免传统非线性分析方法中最为耗时的大规模整体刚度矩阵反复更新和分解运算，取而代之的是仅对小规模Schur补矩阵进行相应运算，实现了计算降维，从而大幅降低非线性分析所需计算消耗。对于地震反应分析问题，需结合运动方程并引入Newmark方法构造动力控制方程，其对应的Woodbury求解公式具有与式(4)完全一致的矩阵表达形式和计算特点。

2 Woodbury+OpenMP并行分析方法

2.1 OpenMP并行机制

OpenMP是适用于共享内存多处理器并行计算的程序设计标准，具有灵活度高、易于编程实现等优点。OpenMP采用Fork-Join的并行模式(Fork即创建或唤醒派生线程，Join即多线程的汇合)，如图2所示，其基本思路为：程序开始时首先由一个主线程执行，当遇到某个并行任务时，程序将派生出多个线程，此时主线程和派生线程将同步进行程序计算，当该并行任务结束时，派生线程退出工作，主线程继续执行后续程序计算任务，遇到下一个并行任务后派生线程将被再次唤醒并参与计算，整个计算程序中可以包含多个并行任务。

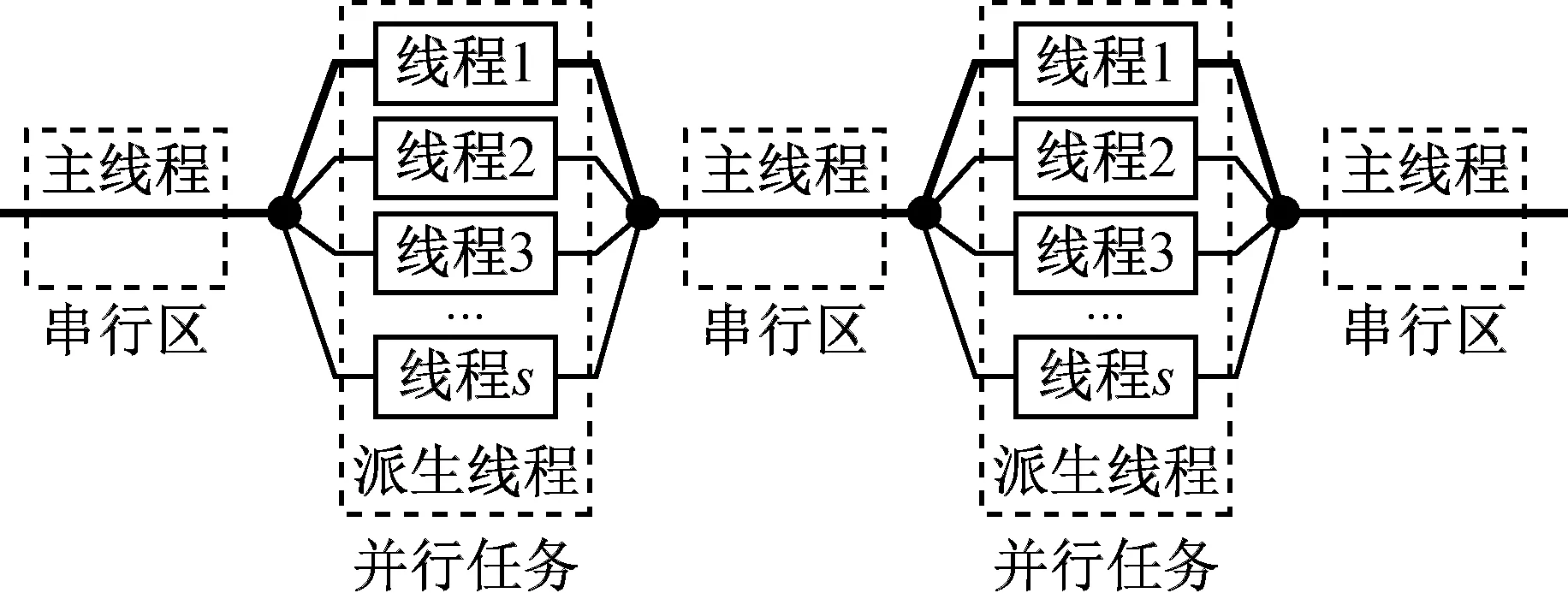
图2 OpenMP并行机制

2.2 Woodbury方法的并行实现

结构进入非线性状态后，需通过迭代完成每个增量计算步的求解。基于Newton-Raphson迭代格式的Woodbury方法非线性分析流程，如图3所示。由图3可知，在开始进行迭代求解之前需首先对结构初始弹性刚度矩阵Ke进行LDLT分解，将分解结果进行存储，以便于在迭代求解过程中随时调用。在每次迭代时，主要包含3个计算步骤，分别是Woodbury公式计算、单元状态确定、非线性相关系数矩阵更新，见图3。本节通过分析上述3个步骤的计算特点，分别设计了基于OpenMP的并行加速方法，各部分具体并行实现方式详述如下。

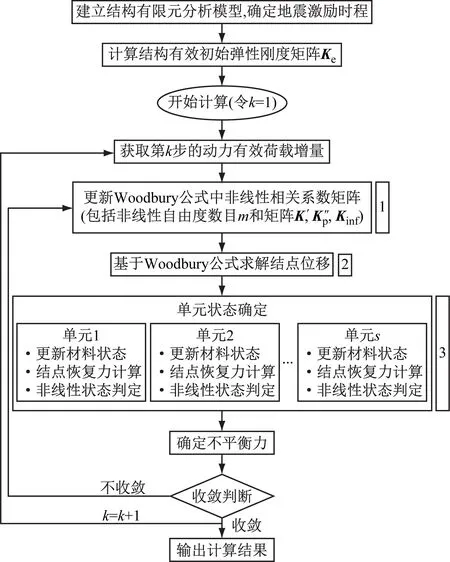
图3 Woodbury方法的迭代求解流程

2.2.1 非线性系数矩阵的并行更新策略

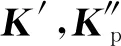
(6)

(7)

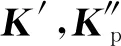
对于系数矩阵Kinf，其为对称矩阵，将式(6)代入式(5)，可得该矩阵的计算表达式

(8)

式中，Aji为与单元j和i有关的子矩阵块，代表单元j对单元i的影响程度，其计算表达式为

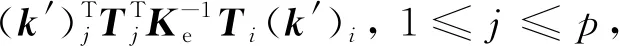
1≤i≤p

(9)

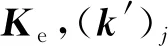
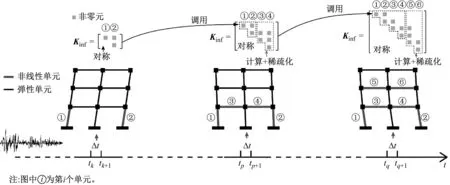
图4 矩阵Kinf更新过程示意图

假设在当前迭代计算步中仅单元p为新进入非线性的单元，同时考虑矩阵Kinf的对称特性，则根据式(8)可知此时仅需计算其第p列数据(包含子矩阵块A1p，A2p，…，App)并对计算结果进行稀疏近似即可。根据式(9)可知各子矩阵的计算互不干扰，为此，本文采用如下步骤实现这一计算过程的并行化。

步骤1首先计算式(10)。考虑到分析前已完成初始弹性刚度矩阵Ke的分解运算，可直接调用矩阵分解结果通过回代完成式(10)计算，回代过程的计算消耗极小，且可实现基于OpenMP并行加速，本文方法利用Intel MKL中Pardiso求解器实现并行回代。

(10)

式中，Sp为计算Kinf第p列数据时所需中间变量。

步骤2计算对角子矩阵App

(11)

步骤3在程序中创建并行区并添加OpenMP指令对，将子矩阵A1p，A2p，…，A(p-1), p的求解及其稀疏判定过程分发到不同线程上进行并行计算。稀疏判定是通过将每个计算出的子矩阵与式(11)计算结果(即App)进行对比实现的，如图5所示。图5中：‖·‖为矩阵范数；τ为预定义的稀疏判定阈值。由图5可知，若某个计算出的子矩阵Aip(1≤i≤p-1)的范数与相应对角块App范数之比小于阈值τ，则可将其近似置零。在程序实际执行时，将这些近似置零的子矩阵直接删除，以降低数据存储需求和后续Woodbury公式的计算复杂度。

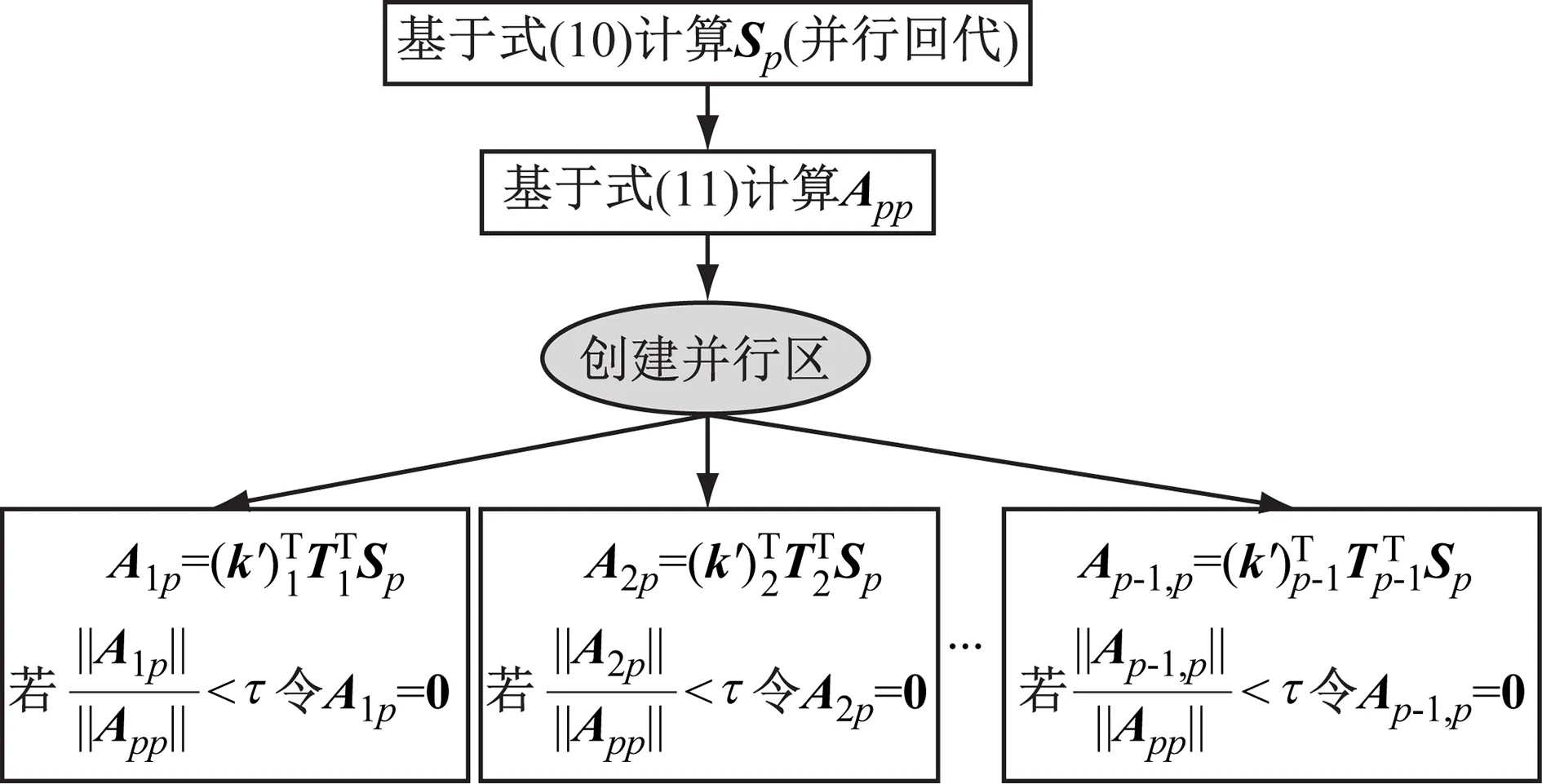
图5 系数矩阵矩阵Kinf的并行更新过程

当某个迭代步中有多个新进入非线性的单元时，对每个单元的相关子矩阵列均执行上述过程，即可实现系数矩阵Kinf的更新。从论述可知，Woodbury公式中与结构非线性相关的系数矩阵均可划分为若干相互独立的子矩阵，各子矩阵在计算时不存在数据交互，因此这些矩阵的更新过程具有较好的可并行特征。上述对于矩阵Kinf的稀疏化处理将导致每次迭代时Woodbury公式计算结果存在一定近似误差，但该误差可通过少量增加迭代次数或引入适当的误差修正策略予以消除，本文采用Yu等提出的基于缩减基的误差修正方法消除这一近似误差带来的不利影响。

本文方法无需在分析前预先设定非线性区域，而是在每次迭代时根据单元状态确定结果实时确定进入非线性的单元位置，根据论述可知，非线性相关系数矩阵更新过程所需计算量与非线性单元的位置无关，仅与这些单元的数量有关，因此该部分计算效率将随非线性区域规模的扩大逐渐降低。

2.2.2 Woodbury公式的并行计算

式(4)仅为Woodbury公式的数学表达，为充分发挥其高效性优势，在实际程序实现时应避免执行耗时的矩阵与矩阵乘法运算。为此，将式(4)从右向左拆解为如表1所示6个计算步，每次迭代时依次执行这6个步骤即可得到Woodbury公式的计算结果。表1中，向量ΔX1～ΔX5均为这一计算过程的中间变量。由表1可知，各计算步仅涉及简单的矩阵与向量或向量与向量之间的运算，每个计算步的计算量均极小。考虑到表1各计算步中涉及的系数矩阵均具有较高稀疏性，本文采用压缩存储格式CSR3(compressed sparse row)对矩阵进行存储并基于此开展相关矩阵运算，以避免零元素相关运算对计算资源的占用，降低计算复杂度。

表1 Woodbury公式计算步骤

对于表1中的第1个和第5个计算步，可直接调用矩阵Ke的分解结果通过回代计算完成，本文基于Pardiso求解器使用并行回代方法进行这两个计算步的快速求解；对于表1中的第2个和第4个计算步，其均为稀疏矩阵与向量之间的乘法运算，根据矩阵运算基本原理可知，等号右边向量ΔX2和ΔX4中各元素的求解过程均互不干扰，因而可基于OpenMP并行方法实现这两个计算步的加速求解；表1中的第3个计算步要求对以Schur补矩阵为系数矩阵的方程组进行求解，可采用基于OpenMP的并行分解和回代方法进行高效计算，本文方法利用Pardiso求解器实现该计算步的并行求解，由于Schur补矩阵的规模通常较小，且可近似化为具有高度稀疏性的矩阵，该步的计算耗时通常极小；表1中的第6个计算步为两个向量的加法运算，其计算量极小，且亦可直接实现OpenMP的并行加速。综上可知，通过将Woodbury公式拆解为6个连续执行的计算步，并基于OpenMP方法对每个计算步的求解进行加速，可实现该公式计算的全过程并行化。考虑到基于矩阵稀疏存储进行相关运算可大幅降低计算过程的时间和空间复杂度，本文方法可极大提高每次迭代时Woodbury公式的实际程序运行效率。

2.2.3 单元状态确定过程的并行实现

单元状态确定的主要作用是在每次迭代时根据计算出的结点位移数据对各单元材料应力、应变、切向模量等参量进行更新，并计算各单元的结点恢复力，以便于更新不平衡力。对于Woodbury方法，还需在单元状态确定过程中判定各单元是否进入非线性，以便于在后续迭代计算中对Woodbury求解公式中非线性相关矩阵进行更新。由于单元状态确定过程中各单元之间不存在数据交互，具有典型的并行化特点，因而可直接在该部分程序代码的开始和结束部位添加OpenMP并行指令对，以实现计算过程的并行加速。

3 算例分析

参考文献[49]建立如图6所示的巨型钢框架结构分析模型，结构共计48层，层高4 m，总高度为192 m，平面尺寸为40 m×40 m，每边均为5跨，跨度均为8 m，图6(b)和图6(c)分别给出了该结构的平立面布置。结构1～24层柱采用Q345钢，其他层均采用Q235钢。使用基于隔离非线性法的纤维梁单元建立该结构分析模型，采用考虑随动硬化的双线性弹塑性本构模型模拟材料非线性行为，其中屈服后刚度系数设为0.01。为充分验证本文建立的并行Woodbury方法对于大规模结构非线性问题的高效性，对模型网格进行适当加密，本例中，将各构件每隔1 m划分一个单元，共计划分40 608个单元，结构的总位移自由度数超过21万(共计215 712)。选取El-Centro地震记录对结构进行非线性地震反应分析，考虑施加平面双向地震激励，其中X方向地面运动的峰值加速度调幅至6.0 m/s2，Y方向地面运动的峰值加速度调幅到5.1 m/s2。计算步长设为0.01 s，截取前20 s地震记录进行分析，共计分析2 000个增量计算步。为验证本文方法的准确性，同时使用有限元软件ABAQUS建立该结构的数值分析模型并选用相同地震记录进行非线性分析，ABAQUS软件模型的网格密度与本文方法相同，单元类型为B32。

(a) 三维模型

本文Woodbury+OpenMP方法、串行Woodbury法和ABAQUS软件分析得到的结构顶点沿X和Y方向的位移时程曲线，如图7所示。由图7可知，并行和串行Woodbury法的分析结果相同，且两者与ABAQUS软件分析结果基本一致。本文方法和ABAQUS软件算得的结构X方向最大顶点位移分别为0.429 9 m和0.425 3 m，仅相差1.08%，Y方向的结构最大顶点位移分别为0.366 7 m 和0.368 5 m，仅相差0.48%，这表明本文方法计算结果具有与ABAQUS软件一致的精度水平。本文方法分析时非线性自由度数目的时程曲线，如图8所示。由于非线性自由度数等于Woodbury求解公式中需实时更新和分解的Schur补矩阵阶数，该值越小表明Woodbury公式的求解效率越高，由图8可知，结构非线性自由度数的峰值为8 379，仅为结构位移自由度数目的3.88%，远小于传统非线性分析方法中需实时更新和分解的整体刚度矩阵阶数(即位移自由度数)，这说明对于局部非线性问题，使用Woodbury公式能够在非线性分析时实现大幅度的计算降维，这也是其计算高效性的主要来源。

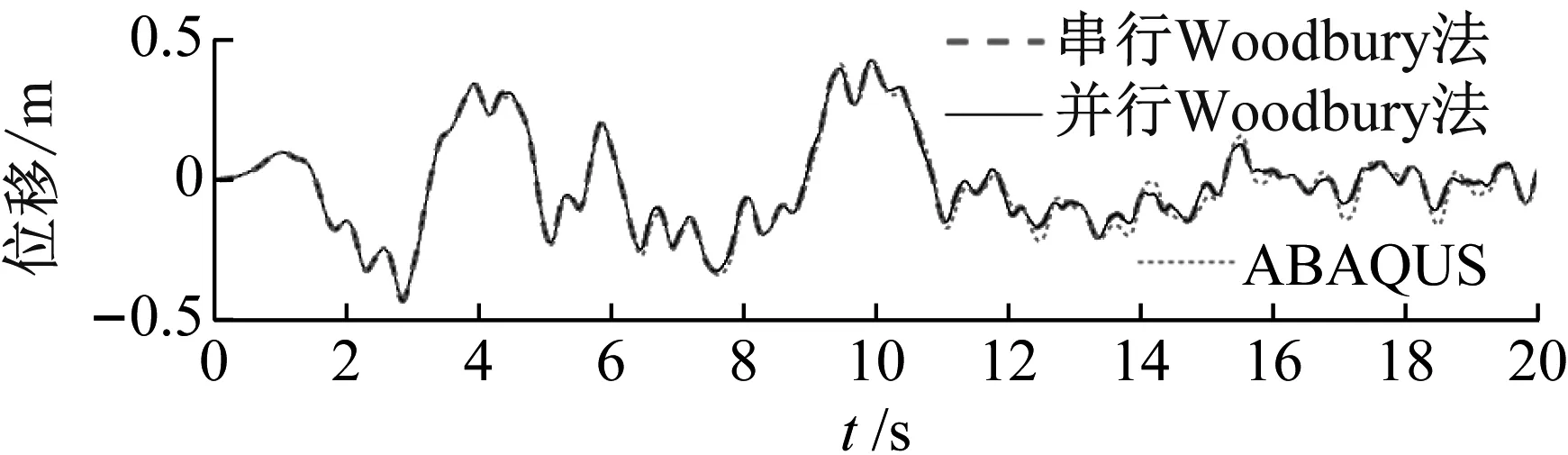
(a) X方向

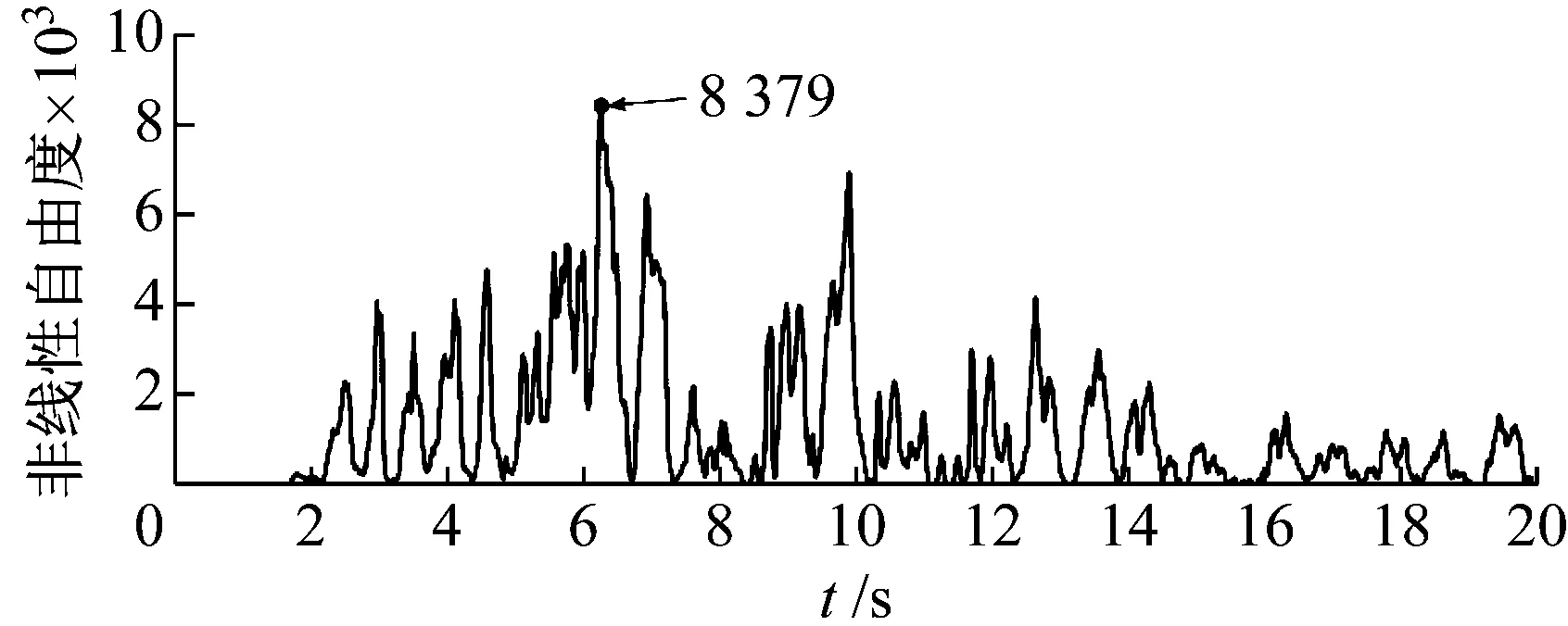
图8 非线性自由度时程曲线

本文方法的所需计算量与结构非线性区域规模有关，对于和本例类似的局部非线性问题，其高效性优势尤为显著，虽然随结构非线性区域规模的提高其计算效率将逐渐降低，但通过结合适当的计算优化策略，如本文采用的Schur补矩阵稀疏优化方法，本文方法的高效性在非线性区域规模较大时依然能够得到保证。若结构出现全局非线性或大部分单元进入非线性的情况，本文方法的适用性将降低，然而，对于工程结构的抗震分析问题，这一极端情况通常较少出现。

为验证本文提出的并行加速策略的有效性，本文Woodbury+OpenMP方法、串行Woodbury方法和ABAQUS软件的总计算耗时，如表2所示。使用的计算平台为装配Intel Core i9-10920X处理器的个人PC机，处理器核数为12。可以看出，本文方法仅耗时967 s，为串行Woodbury分析方法计算耗时的18%，这表明对于该算例，本文并行方法的加速比为5.5。此外，ABAQUS软件的计算耗时约为9.5 h，分别为串行和并行Woodbury方法计算耗时的6.3倍和34.6倍，并行与串行Woodbury方法各部分的计算耗时，如表3所示。可以看出，本文方法在单元状态确定部分的并行效率最高，这主要是由于该部分计算时各单元完全独立，不存在串行计算代码，无需执行额外的进程创建与销毁工作。由表3可知，系数矩阵更新和Woodbury公式计算的并行效率虽然相对较低，但此两部分的计算耗时依然能够实现较大幅度的降低(分别降低了60.4%和49.8%)。由于Woodbury求解公式本身仅需极小的计算消耗，串行分析程序的主要计算耗时集中于单元状态确定部分和矩阵更新，因而从这两部分节约出的较高计算时间有助于大幅提升本文方法的整体并行计算效率。

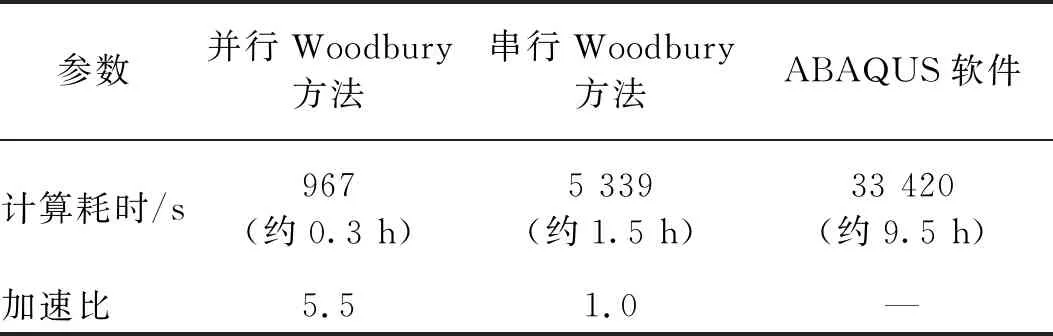
表2 计算耗时对比

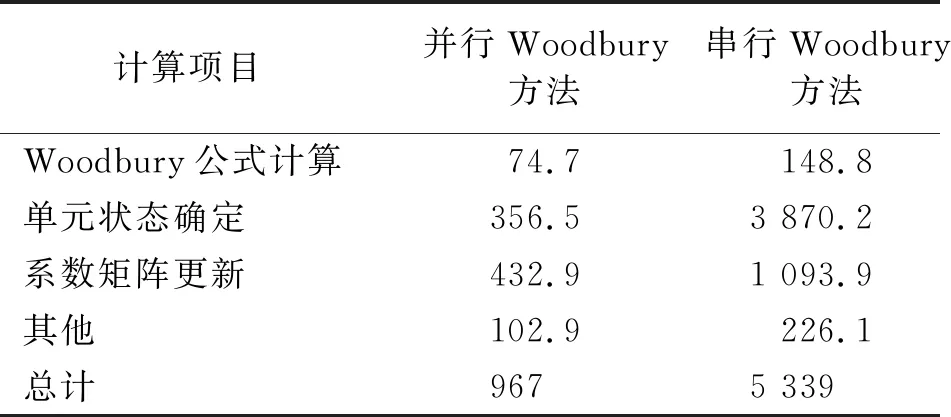
表3 Woodbury方法不同计算部分耗时统计

4 结 论

本文利用OpenMP并行编程模式，针对基于Woodbury公式的结构非线性动力反应分析方法，通过对其迭代求解过程中的主要3个主要计算部分(非线性相关系数矩阵更新、Woodbury公式计算和单元状态确定)进行并行加速，提出了一种用于高效非线性地震反应分析的Woodbury+OpenMP方法。本文具体结论如下：

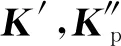
(2) Woodbury公式在实际应用时可以拆解为依次执行的6个计算步，各计算步仅涉及矩阵与向量或向量与向量之间的运算，由于各计算步均可实现基于OpenMP并行化，本文方法能够大幅提升该公式的实际程序执行效率。

(3) 本文方法中，Woodbury公式的使用避免了传统非线性地震反应分析方法所需的整体刚度方程反复更新求解，进一步结合并行计算技术，本文方法在保证计算精度与传统非线性分析方法相当的前提下可大幅提升结构地震反应分析效率。