基于SMO的PMSM无模型无差拍预测电流控制

郭义超，石上瑶，刘亚楠，陈嘉伟

(1.中北大学机械工程学院，山西 太原 030051)(2.中北大学软件学院，山西 太原 030051)

由于永磁同步电机(permanent magnet synchronous motor, PMSM)稳态精度高、结构简单、动态响应快，在诸多工业领域(如机器人、3D打印、轨道交通等)被大量使用[1-2]。模型预测控制(model predictive control,MPC)算法依靠系统参数建立控制系统[3]，由于不稳定的电机参数会降低算法的控制性能，因此MPC对参数变化较为敏感[4]。但在实际的工作环境中，PMSM的电阻、电感等电机参数会因温度等工作环境的变化而出现参数失配[5]。

法国学者Fliess[6]为解决电机参数失配问题，提出了一种新的控制算法——无模型控制(model-free control，MFC)，提高了控制系统的性能。许令亮等[7]将扩张状态观测器(extended state observer，ESO)添加到MFC中，当电机出现参数失配时，能够保证电机的控制性能。Zhuo等[8]在无差拍预测控制(deadbeat predictive control, DPC)中添加MFC，结合在线参数辨识实现了无模型无差拍预测电流控制(model-free deadbeat predictive current controller,MFDPCC)，该方法能有效提高电机鲁棒性。

综上所述，利用在线参数辨识或ESO，能够有效解决因参数失配而引起的控制效果下降的问题，提高系统的抗干扰能力。但在线参数识别因计算量较大而导致反应速度降低，而ESO则是需要调试的参数较多，使得控制系统较为复杂。由此本文提出了一种基于改进滑模观测器的无模型无差拍预测电流控制(model-free deadbeat predictive current controller-sliding mode observer,MFDPCC-SMO)算法。

1 PMSM的数学模型

1.1 PMSM在理想情况下的数学模型

在忽略一些次要因素并进行坐标变换后，PMSM在两相旋转坐标系下的理想数学模型可表示为[9]：

(1)

式中：ud,uq分别为定子的d,q轴电压；id,iq分别为定子的d,q轴电流；Rs为定子相绕组电阻；ψf为转子磁链；ωe为转子电角速度；Ld,Lq分别为定子d,q轴电感，对于表贴式永磁同步电机而言，Ld=Lq=Ls，其中Ls为定子电感的标称值。

1.2 PMSM的新型超局部模型

本文采用单输入单输出新型超局部模型来替代PMSM的数学模型。新型超局部模型不使用任何电机参数，以电压矢量为控制变量，定子电流的变化为输出变量，为电流环建立新型超局部模型[10]。

(2)

式中：αd,αq分别为d,q轴的电流系数；βd,βq为d、q轴的电压系数；hd,hq为电机在d,q轴的未知非线性部分。

通过比较电机理想状态模型方程式(1)和新型超局部电机模型式(2)，可得：

(3)

虽然α和β两个系数会因电机参数变化而变化，但可以通过调整h的值来达到控制目的，保持较高的控制性能。

2 设计无模型预测电流控制器

2.1 基于新型超局部模型的预测模型

假设控制系统的采样周期是Ts，PMSM预测模型的转子旋转坐标系统通过使用一阶欧拉方程进行离散化。PMSM的离散状态方程为：

(4)

2.2 代价函数的选择

为了使实际电流接近参考电流，需要选择合适的代价函数来比较二者之间的误差，以期达到期望的控制效果。代价函数为：

(5)

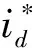
在控制过程中，实际电压与参考电压之间存在一个周期的延迟，在KTs时刻选择的最佳电压，在(k+2)Ts时刻才会输出，这种延迟会降低系统的控制性能。为消除这一误差，本文通过延时补偿的方法来降低对控制系统的影响。先由上一周期的最佳电压矢量计算得到ud、uq，代入式(4)中得到(k+1)Ts时刻的电流值，再利用式(4)计算(k+2)Ts时刻的电流值，则代价函数改为：

(6)

3 设计离散SMO未知部分

3.1 建立SMO结构模型

为了更加准确地估计未知部分，本文设计了如下的新型滑模观测器来获取未知部分的观测值。

(7)

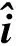
(8)

式中：a为常数，用于调节函数在0附近的斜率，从而降低抖振带来的影响。

(9)

式中：h为滑模观测器未知非线性部分，h=[hdhq]T。

本文选取d轴电流id和q轴电流iq作为控制变量，选取电流误差变量e作为滑模面，设计适当的矩阵γ时，由式(9)确定的观测器误差方程将在有限时间内收敛到0。

3.2 滑模观测器的离散化

在实际应用中，滑模观测器通常在离散情况下工作，所以需要推导它的离散形式。若采样周期Ts足够小，式(10)可如下表示：

Tsγsgn(e(k))

(10)

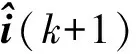
(11)

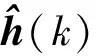
4 仿真与实验

4.1 仿真结果分析

为验证本文改进的无模型预测控制算法的有效性，根据上述推导的数学模型建立MATLAB/Simulink仿真模型，分别对MPCC和MFDPCC-SMO两种方法进行验证。

MFDPCC-SMO算法的MATLAB/Simulink仿真模型如图1所示，其中PID模块的微分系数D设置为0。

图1 MFDPCC-SMO仿真模型

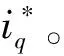
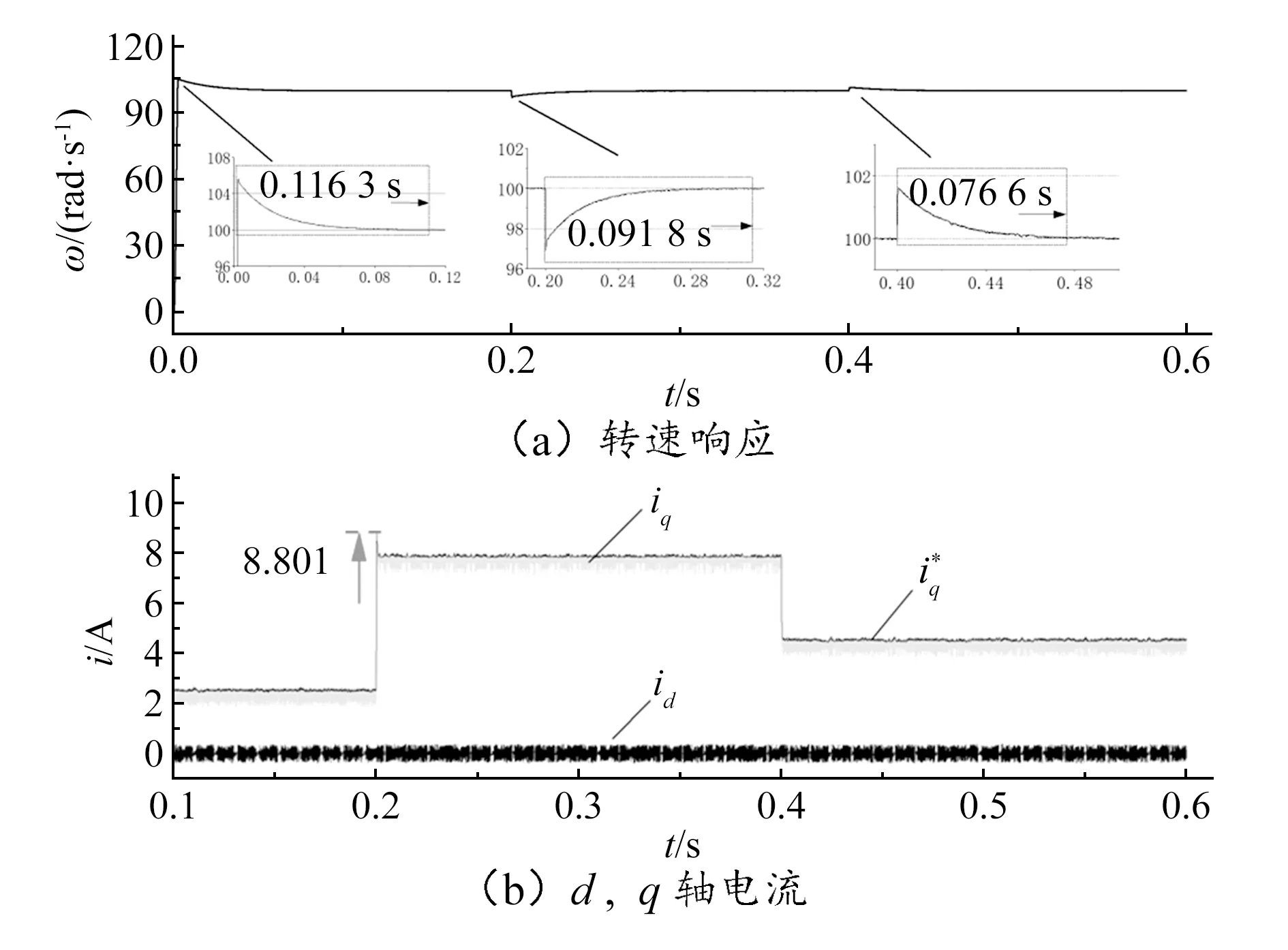
图时MPCC仿真结果

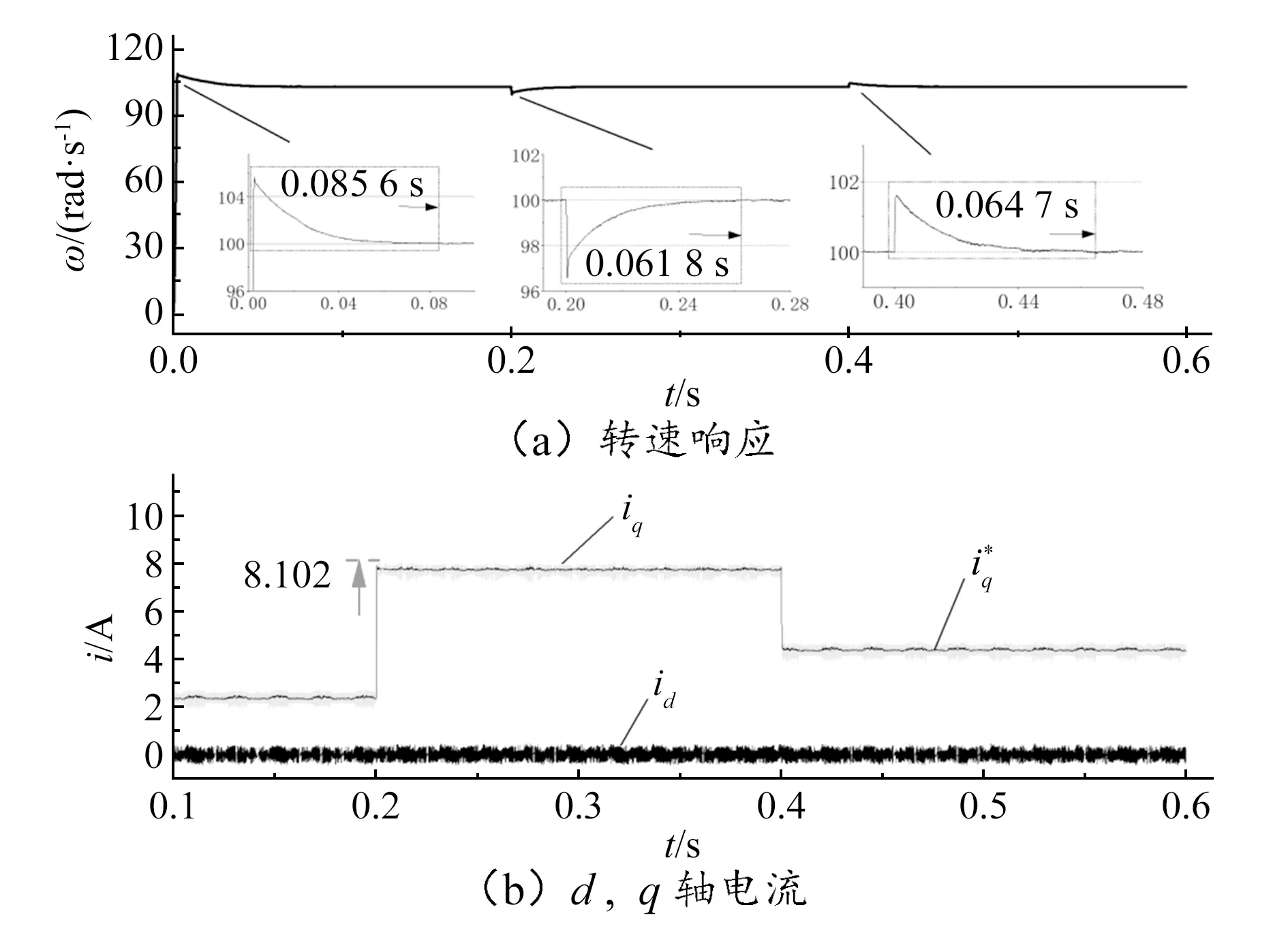
图时MFDPCC-SMO仿真结果

图时MPCC仿真结果

图时MFDPCC-SMO仿真结果

仿真结果表明，MFDPCC-SMO算法能够更好地追踪电流的参考值而不受电机参数变化的影响，同时MFDPCC-SMO算法在负载转矩变化时的转速响应更快，证明MFDPCC-SMO算法有较强的鲁棒性。

4.2 实验结果分析

为验证本文提出的MFDPCC-SMO算法，搭建如图6所示半实物仿真平台。该实验平台基于MATLAB/Simulink进行伺服控制系统算法模型设计，并能够自动生成代码，下载到目标机上运行，便于PMSM控制方法的研究和验证。

图6 实验平台

图时MPCC实验结果

图时MFDPCC-SMO实验结果

图时MPCC实验结果

图时MFDPCC-SMO实验结果

从实验结果可以看出，当电机参数失配时，面对负载转矩变化，MFDPCC-SMO算法具有比MPCC算法更快的转速响应速度和更好的电流跟踪效果。

5 结束语

为了提高PMSM系统在参数失配情况下的控制性能，结合无模型控制和无差拍控制，提出了一种基于改进滑模观测器的无模型无差拍预测电流控制算法。基于新型超局部模型的MFCC控制不涉及电机参数，能够避免对电机参数的依赖；利用DPCC和SMO能够有效地估计系统扰动，更好地追踪电机电流参考值，提高电机转速响应速度。与MPCC算法相比，MFDPCC-SMO算法在电机参数失配时，能够抑制参数变化对电机控制效果的影响，能够较好地跟踪参考电流，并能快速达到目标转速，具有较强的鲁棒性和抗干扰能力。