基于格拉姆角场和卷积神经网络的滚动轴承微弱故障位置辨识研究

郑 煜，穆龙涛，赵俊豪

(陕西工业职业技术学院机械工程学院，陕西 咸阳 712000)

滚动轴承是转子机械的重要基础部件[1]，在关键设备中起重要的支撑作用[2]，其运行状态往往决定了机械设备能否正常运行[3-4]，因此针对滚动轴承开展有效监测、及时发现可能存在的故障，对于保证机械设备的可靠运行和降低维修成本具有重要意义[5]。针对滚动轴承弱故障位置辨识问题，多位学者[6-8]分别提出了经验模态分解、混合域特征提取、支持向量机等不同方法。然而由于滚动轴承微弱故障信号包含着大量非线性信息，从而使得这些传统方法在诊断时适应性欠佳。在相关研究中[9-12]，卷积神经网络(convolutional neural network,CNN)在数据分类中取得了良好的效果，因此本文选择卷积神经网络作为滚动轴承弱故障位置辨识的方法。在轴承弱故障辨识中，轴承振动信号存在着大量原始时序特征，其所包含的信息对辨识的准确性具有重要意义。但直接使用原始振动信号开展网络训练，会因数据量大而导致训练时间长，因此需要在保留信号整体信息的情况下压缩信号长度。

综上，笔者使用分段聚合近似(piecewise aggregate approximation, PAA)对信号进行降维压缩处理，随后使用格拉姆角场(Gramian angular fields, GAF)将轴承一维振动信号转化为二维图像，再将图像输入卷积神经网络以实现微弱故障辨识。

1 格拉姆角场

格拉姆角场能够将一维时间序列转换为二维图像[13-14]。对于给定的一维时间序列X={x1,x2,…,xn}，按式(1)归一化至[-1,1]区间：

(1)

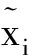
(2)

使用式(3)或式(4)计算格拉姆角场[15]：

(3)

式中：GASF为格拉姆和角场。

(4)

式中：GADF为格拉姆差角场。

格拉姆角场具有以下特点：1)主对角元素包含所有时间戳对应的值；2)角场中第i行第j列表示两时刻的数据相关性。因此，可以在保留一维时间序列原始信息的情况下反映出不同时刻的数据相关性。格拉姆角场图如图1所示。

图1 格拉姆角场图

2 实验数据

2.1 实验数据介绍

本文实验数据由深沟球轴承(型号为6205-2RS JEM SKF)获得[16]。实验前通过电火花加工，在实验轴承的内圈、外圈和滚动体上分别制造出直径为0.18 mm的单点微弱故障凹坑。振动信号通过由磁性底座布置在驱动端轴承座负荷区的加速度传感器采集，并采用16通道数字录音记录器采集加速度传感器数据，采样频率为12 kHz。实验装置如图2所示。

图2 实验装置

2.2 数据处理

为了给卷积神经网络提供训练样本，本文在原振动信号中连续截取一定长度的数据点构建子样本，从而将原信号转化为多段样本，如图3所示。

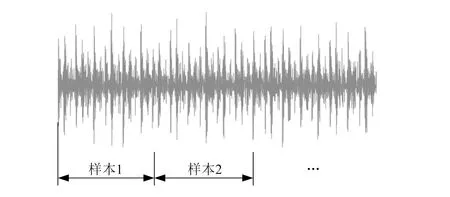
图3 训练样本划分方式

在截取时，如果子样本长度过长容易导致训练时间过长；如果子样本长度过短，则不能够反映信号所包含的整体信息。因此，本文将子样本长度确定为512个数据点位。

2.3 分段聚合近似

分段聚合近似是一种采用等时间分辨率数据序列对原时间序列数据重新构建的方法，对于多数一维时间序列具有良好的数据降维效果。分段聚合近似可按式(5)计算[17]：

(5)

急性肾衰伤患者分级：患者的急性肾衰伤分级根据全球肾病预后组织制定的急性肾衰伤进行判断，主要分为三期：急性肾衰伤Ⅰ期：血清肌酐值增加超过26.5 μmol/L，或者增加基线值在1.5～1.9倍；急性肾衰伤Ⅱ期：血清肌酐值增加基线值在2.0～2.9倍；急性肾衰伤Ⅲ期：血清肌酐值增加基线值在3倍以上。

3 卷积神经网络

本文设计的卷积神经网络共有18层，分别是1个输入层、3个卷积层、3个批量归一化层、4个分线性激活层、3个最大池化层、2个全连接层、1个Softmax函数层、1个输出层。卷积神经网络结构参数见表1。

表1 卷积神经网络各层参数

在表1中，由于ReLU函数收敛速度快，表现性能好，因此选择ReLU函数作为激活函数；在激活函数前，添加批量归一化层以克服梯度饱和问题；使用动量随机梯度下降法(stochastic gradient descent with momentum, SGDM)作为训练方法，引入小批量方法(minibatch)以克服SGDM因样本差异而出现的算法不稳定问题。

该网络minibatch数为128，初识学习率为0.01，学习率减小因子为0.1，学习率调整周期为20，在每轮训练或验证前打乱数据，最大轮数为40。

4 弱故障位置辨识

4.1 样本数据集

实验数据样本分别取自正常和故障轴承，其中故障为单点故障，分为内圈、外圈或滚动体故障。按照512数据位长度划分为子样本，采用PAA算法将子样本长度压缩至64，分别制作子样本格拉姆和/差角场图，得到正常样本1 450个，滚动体故障样本950个，内圈故障样本952个，外圈故障样本953个，同时以7∶3的比例随机划分成训练集与验证集。训练设备的CPU为intel core i5-7500H，其具有16 GB内存，GPU为1050Ti，4 GB显存。

4.2 故障位置辨识

将样本图像输入卷积神经网络，经40轮训练后停止。各轮训练中的验证准确度如图4所示。

图4 格拉姆和/差角场验证准确度对比

从图中可以看出，以格拉姆差角场作为训练样本时，前几轮验证准确度提升迅速，在第4轮后验证准确度维持在98%上下；以格拉姆和角场作为训练样本时，前几轮验证准确度提升相对较慢，在第14轮后维持在97%上下。完成训练，格拉姆差角场最终验证准确度为98.30%，格拉姆和角场为97.14%。

绘制格拉姆和/差角场的验证样本混淆矩阵，如图5所示。统计不同故障位置样本的验证准确度，见表2。

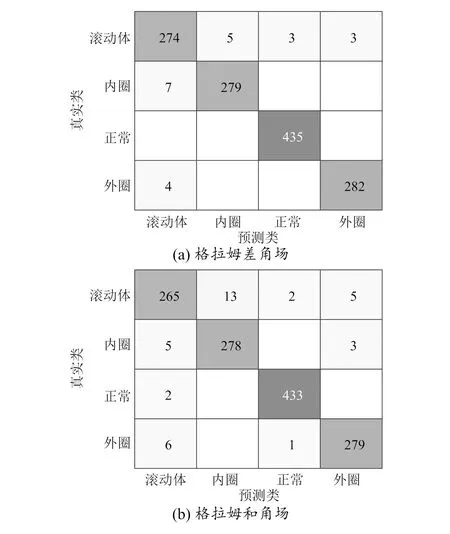
图5 格拉姆和/差角场混淆矩阵

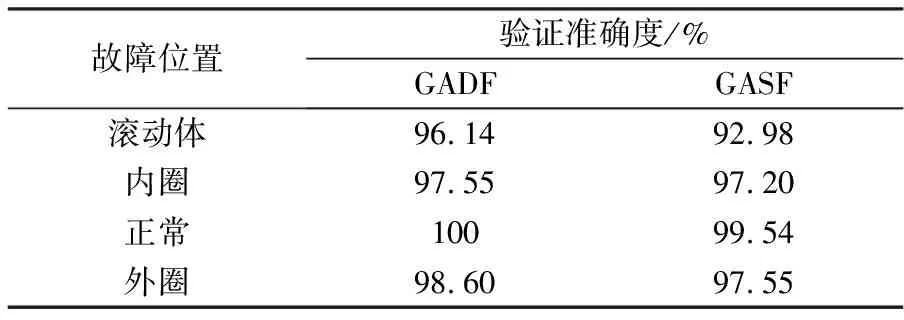
表2 格拉姆和/差角场对各类型样本的验证准确度

从图5和表2可以看出，无论是正常状态还是滚动体故障、外圈故障或内圈故障，格拉姆差角场的验证正确率均高于格拉姆和角场。因此可以认为，格拉姆差角场在滚动轴承弱故障辨识中具备更好的辨识效果。同时，格拉姆和/差角场均为对正常样本的辨识准确度最高，对滚动体样本的辨识准确度最低，这可能与滚动体故障特点相对复杂、特征信号成分多有关。

5 结束语

本文使用卷积神经网络实现了滚动轴承的微弱故障位置辨识，相较于传统诊断方法，本文方法体现出了良好的轴承微弱故障信号适应性和较高的验证准确率，同时本文方法解决了传统方法中繁琐的手动设计滤波和特征选择问题，使得诊断过程更加智能，并能适应未来海量的工业大数据。研究过程中也暴露出滚动体故障样本辨识度相对较低的问题，针对该问题，后续可以从进一步提升网络辨识能力的角度进行改进。