游离粒子摩擦辅助电铸工艺优化与仿真分析
王 昆 陈世杰
(同济大学 机械与能源工程学院,上海 201804)
游离粒子摩擦辅助电铸技术采用陶瓷球等硬质微粒作为摩擦介质,在旋转机构或平动机构的带动下,紧贴阴极面做自转、滑动、振荡复杂运动,是借助机械研磨和摩擦挤压作用整平沉积层的一种技术[1-2]。电沉积过程中,游离粒子自由运动,不断摩擦挤压阴极表面,有着整平抛光表面、除氢、提高传质速度以及均匀电流密度分布等作用[3-4]。该项技术可以解决传统电铸工艺存在的针孔、麻点以及结瘤等问题[5-6]。自由粒子与阴极表面的摩擦是改善阴极电铸质量的直接因素。但是,该项技术在阴极表面垂直空间存在摩擦力分布均匀性差的问题,且少有学者研究。章勇等人提出了更改阴极放置方式的方法,但是在阴极必须垂直放置,并不通用[7]。
针对这一问题,本文提出一种游离粒子加压摩擦辅助电铸的方法,且其推导的理论模型显示了其有效性。为了验证模型的准确性,采用离散元软件Rocky DEM建立压力板游离粒子颗粒模型,研究电铸过程中加压前后游离粒子在垂直空间对阴极表面压力的变化情况。结果显示,仿真试验结果与理论模型预测结果相一致。
1 试验设备与数学模型搭建
1.1 试验设备
仿真模型采用的电铸结构如图1所示。装置外接直流电源进行电铸,减速电机连接主轴,便于控制中间回转体阴极的旋转速率。游离粒子充斥在阴阳两极之间。环形压力板覆盖在游离粒子区域上方,对粒子施加向下的压力。采用烧杯水浴加热的方式控制电铸液温度。

图1 游离粒子与阴极示意图
1.2 游离粒子压力板数学模型
未加入电铸液时,对图1中紧贴着阴极外表面上任一单元体进行受力分析,可表示为

式中:F为压力板压力;ρ为游离粒子整体等效密度;g为重力加速度;x为与压力板下表面的距离;A为游离粒子区域水平面积。
根据胡克定律,在弹性变形范围内,有
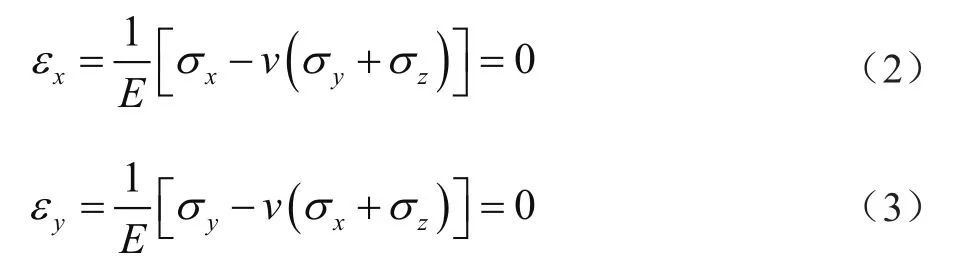
式中:E为游离粒子整体等效弹性模量;ν为游离粒子整体等效泊松比。
由式(1)、式(2)以及式(3)联立求解,可得

深x处单位面积阴极表面摩擦力为
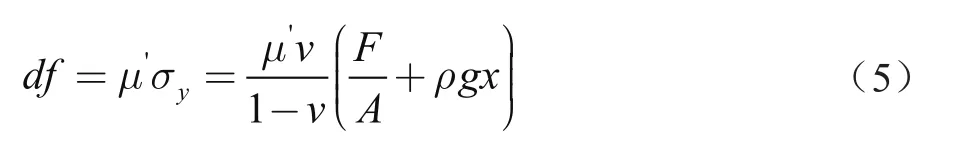
式中:μ´为粒子与阴极的摩擦系数。
加入电铸液后,阴极外表面受力情况和阴极表面摩擦力可表示为

式中:μ为加入电铸液后的游离粒子与阴极表面的摩擦系数。
由式(7)可知,压力板加压优化后,游离粒子区域上下界与阴极表面摩擦力比值从缩小到,可得

式中:ρ液为电铸液密度;d为游离粒子直径;l为阴极高度。
均匀系数Cu(F,l,d)是与压力值F、阴极高度l以及游离粒子直径d有关的不均匀系数函数表达式。函数值越接近于1,摩擦力分布越均匀。由式(8)得知,增大压力板的压力值或减小游离粒子直径与阴极高度比,均可以改善阴极摩擦辅助电化学沉积的作用效果。
2 游离粒子数学与仿真模型
2.1 建模参数确定
仿真参数包括结构参数和材料参数。设阴极高度为150 mm,直径为100 mm,转速为3.14 rad·s-1,游离粒子直径为5 mm,阴阳极间距为30 mm,压力板下压距离为5 mm。
电铸仿真模型包括游离粒子、阴极、阳极框与压力板等。游离粒子材料为氧化锆珠,密度为5.85 g·cm-3,弹性模量为2.2×105MPa,泊松比为0.30。阴极材料为6061铝合金,密度为2.75 g·cm-3,弹性模量为6.89×104MPa,泊松比为0.33。阳极框材料为亚克力板,密度为1.19 g·cm-3,弹性模量为3.16×103MPa,泊松比为0.32。压力板选用绝缘体材料。
各材料接触参数可通过静摩擦参数测试装置测得,所用材料的碰撞恢复系数用自制碰撞恢复系数测量装置得出[8],如表1所示。
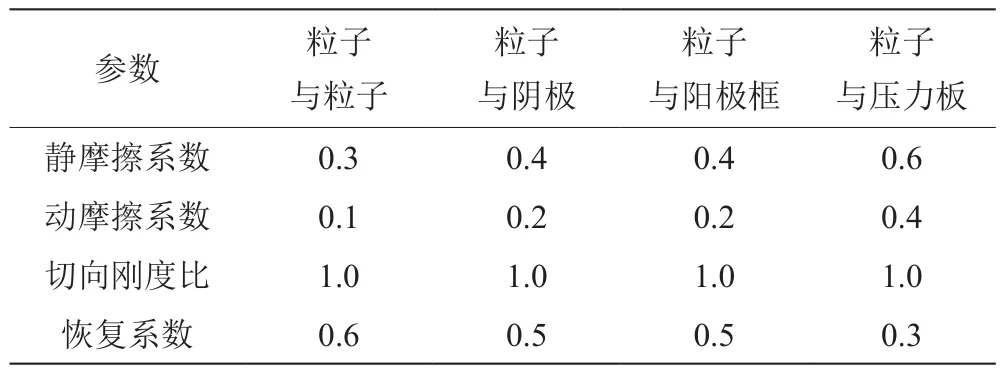
表1 材料接触参数
2.2 电铸液流场模型确定
采用ANSYS Workbench平台与Rocky DEM平台,进行计算流体动力学-数字高程模型(Computational Fluid Dynamics-Digital Elevation Model,CFDDEM)耦合仿真。在ANSYS Fluent模块中设置电铸液模型的循环状态,根据实际电铸液循环流向,设定流场进出口为阴阳极间槽口的上下边界,并选择标准k-ε紊流模型。定义电铸液的流体密度为1 225 kg·m-3,运动黏度为2.98×10-3Pa·s,电铸液入口流速为0.005 m·s-1。电铸液温度设定为25 ℃,大气压强为1.01×105Pa,选择稳态求解。
2.3 游离粒子压力板仿真模型
将阴极模型以.x_t文件的格式导入WorkBench,压力板与阳极框三维模型以.stl文件的格式导入Rocky DEM,如图2所示。

图2 游离粒子压力板仿真模型
2.4 接触模型设置
在Rocky DEM中,游离粒子设定为5 mm直径球体。由于游离粒子数量多,碰撞后仍会挤压在一起,不符合硬球接触模型的瞬态碰撞条件,所以颗粒选择软球接触模型,法向力选择Hysteretic Linear Spring模型,切向力选择Linear Spring Coulomb Limit模型,数值软化因子选择1。
3 仿真试验结果分析
该模型中,阴极保持匀速旋转,游离粒子填充在阴极与阳极之间。压力板设置在游离粒子上方,并使其延时向下运动直至挤压粒子。通过求解阴极表面的压力变化曲线,可以得到游离粒子在受压前后摩擦辅助电铸的效果变化情况。整个仿真过程时间设置为18 s,其中第7 s游离粒子仍在注入的时刻截图如图3所示,所有向下的箭头代表CFD耦合的电铸液流场方向。为便于观察,图3隐藏了作为游离粒子碰撞边界的阳极框模型。
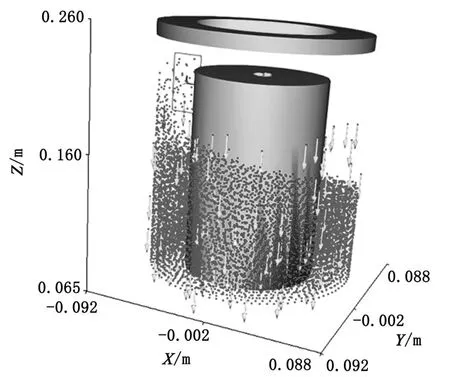
图3 仿真过程截图
由于阴极结构为对称回转体,截取阴极表面四处相互对称的垂线上相等间距(70 mm)的底部、中部、顶部3点,则它们在表面法线方向上的平均节点力随时间的变化曲线如图4所示。

图4 阴极表面不同位置处节点力变化曲线
1~10 s为游离粒子持续注入时段,阴极侧面总体所受的压力不断上升,第10 s达到峰值。11~14 s为纯阴极旋转过程,压力板持续下降但未接触粒子表面,此时游离粒子逐渐分布均匀,阴极表面压力轻微浮动。从图4可以看出,阴极侧面与游离粒子接触处,底部所受压力最大,顶部受压力最小,从下到上所受压力不断减小,与理论模型预测相一致。15 s后,随着压力板下降并逐渐接触挤压游离粒子,阴极表面压力明显上升,且底部和顶部的相对压力差逐渐减小。阴极侧面压力随时间的变化曲线如图5所示。
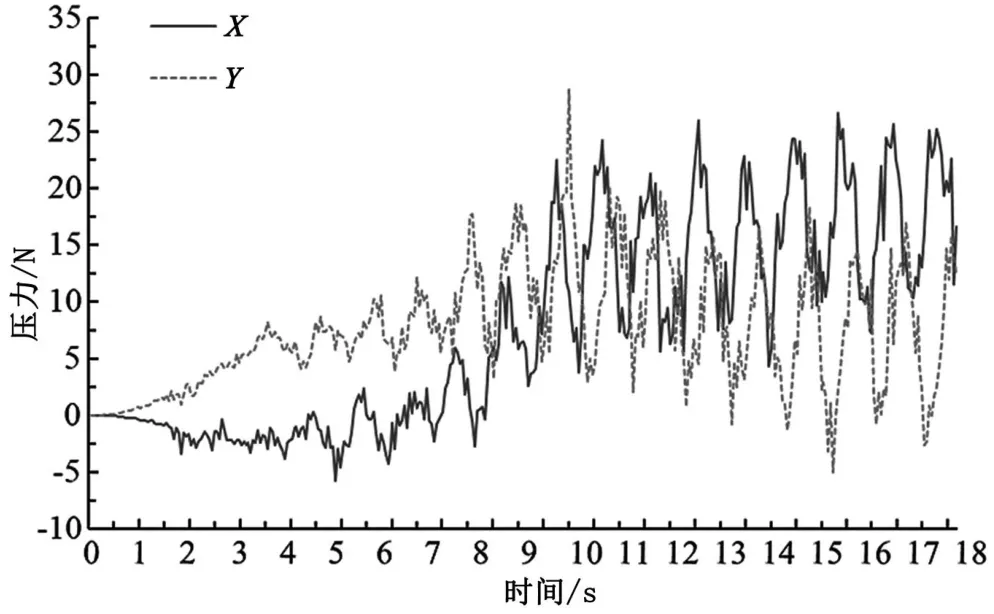
图5 阴极表面x与y方向的压力变化曲线
图5展示了X和Y这2个垂直方向阴极表面平均压力的变化曲线。曲线波动幅度与粒子和阴极的接触位置有关。可以看出,曲线一开始波动幅度较小,随时间的推移,2条曲线的波动幅度逐渐变大至一定范围。随着粒子总量的增加,阴极表面所受平均压力逐渐增大。随着压力板给粒子施加的压力逐渐增大,阴极表面2个方向上所受的平均压力均有不同程度的降低,表明利用压力板对游离粒子施加压力能够有效缓和阴极表面上下界的平均压力。
4 结语
本文搭建了压力板加压下游离粒子摩擦辅助电铸模型,经过理论推导得出了压力-摩擦力分布均匀性的方程。方程显示,通过增大施加在压力板的压力值和减小游离粒子直径与阴极高度之比,可以明显改善阴极摩擦辅助电化学沉积的作用效果。利用ANSYS Fluent模块与离散元软件Rocky DEM进行CFDDEM单向耦合仿真,验证了理论模型的准确性,可为游离粒子加压的优化研究提供参考。

