三排圆柱滚子轴承接触特性分析

王明伟 王燕霜* 王加祥 王子君 程 冬 郑广会

（1.齐鲁工业大学（山东省科学院），济南 250353；2.洛阳轴研科技有限公司，洛阳 471039；3.烟台天成机械有限公司，烟台 264006；4.山东金帝精密机械科技股份有限公司，聊城 252035）

三排圆柱滚子轴承作为风电机组的主要零部件，其工作寿命和可靠性直接影响整个风电机组系统的使用寿命，一旦在运转过程中出现故障，将难以对其进行维修。目前，对于轴承载荷分布、接触特性以及轴承寿命等方面的研究，主要集中在球式滚动轴承[1-4]，而对于三排圆柱滚子轴承的载荷分布和接触特性的研究相对较少。常用的三排圆柱滚子轴承所受载荷一般为偏心载荷。除了承受轴向载荷和径向载荷外，还需要承受倾覆力矩[5]。姜笑颖等人对理想Hertz接触下的三排圆柱滚子轴承进行分析，得出在轴向力和倾覆力矩单独作用下的每一排滚子的载荷分布[6]。但是，轴承的滚柱尺寸较大，滚柱长度超出了赫兹接触理论中的有限长度，因此在滚柱边缘位置的分析与实际情况有所偏差。针对这一问题，冯建有等人在非理想赫兹接触特性下分析三排圆柱式滚子轴承，结合冯米塞斯理论得到了轴承的次表面应力分布[7]。国外学者GÖNCZ分析了轴承游隙对三排圆柱滚子载荷分布的影响[8]。在此基础上，MAREK分析了轴承各滚动体载荷分布的形成机理，并针对滚子局部应力进行详细描述[9]。

现有的文献仅给出了接触力的求解方法和最终数值，缺乏对接触载荷分布的分析，尤其是缺乏三排滚子接触载荷分布和接触特性异同的详细分析。文章以某型号真实三排圆柱滚子轴承为例，建立其接触力学模型，分析计算结果，比较每一排滚子接触特性的异同，以改善三排圆柱滚子轴承接触状况，为延长轴承疲劳寿命提供理论和分析基础。

1 三盘圆柱滚子轴承接触力学模型

1.1 滚子受力分析

轴承外部负载如图1所示。因为每排滚子在运转中承受载荷的情况不同，所以需要对每列滚子受力状况分别进行分析。第一排和第二排滚子承受轴向力为Fa、倾覆力矩为M以及第三排滚子承受径向力为Fr。

图1 三排圆柱滚子轴承的受力情况

1.2 接触力学模型

由于三排圆柱滚子轴承的第三排滚子轴承径向力，在每一个第三排滚子位置角ψ处，滚子与滚道面接触的法向趋近量可表示为

式中：δr为径向位移；Gr为径向游隙。

第三排滚子任意位置角处接触力可表示为[10]

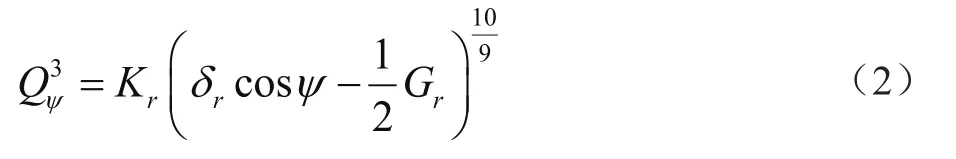
式中：Kr为第三排滚子与滚道负载变形常数。

由于三排圆柱滚子轴承所受的轴向力和倾覆力矩由第一排、第二排滚子承受，在外部载荷作用下，轴承内圈产生移动，两排滚子与滚道接触面产生的法向趋近量可表示为

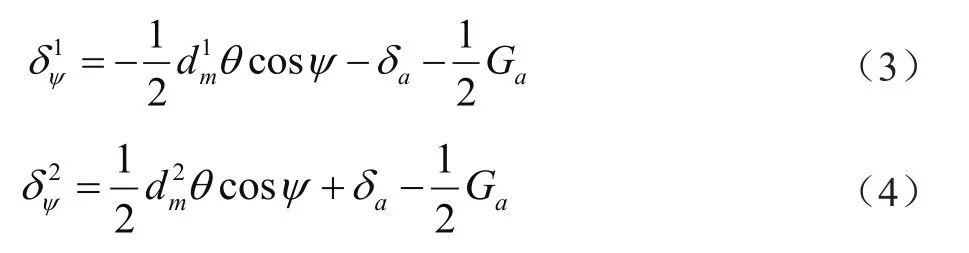
式中：δa为轴向位移；Ga为轴向游隙；dm1为第一排滚子分度圆直径；dm2为第二排滚子分度圆直径；θ为倾角位移。

任意位置角处第一排与第二排滚子所承受的载荷为

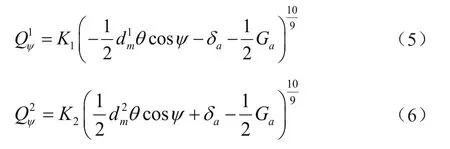
式中：K1为第一排滚子与滚道负载变形常数；K2为第二排滚子与滚道负载变形常数。

根据力的平衡，可得三排圆柱滚子轴承的平衡方程组为

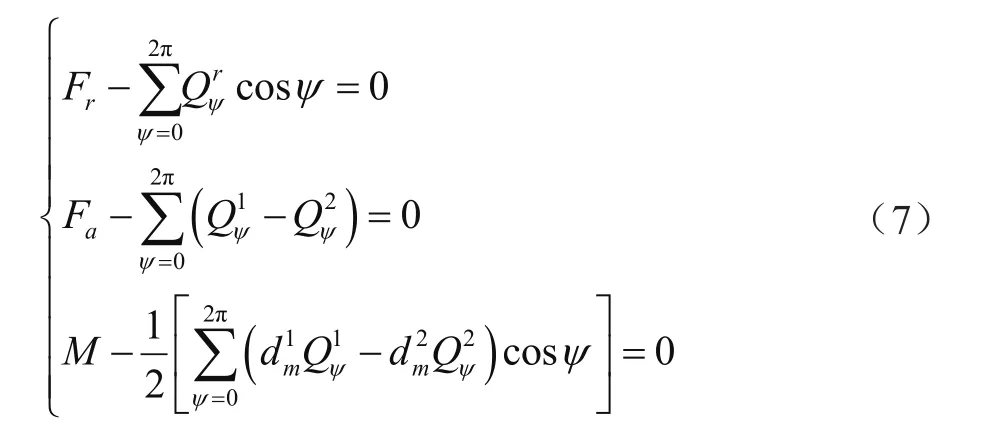
联立各式即可求解每一排滚子的位移和负荷。

2 表面接触应力

根据赫兹接触理论，当发生接触的2个圆柱体轴线相互平行时，假设接触面的宽度为2b，滚动体的有效长度为l，弹性趋近量为δ，则载荷Q、负荷线密度q以及长度l三者的关系为[10]

矩形接触面半宽为

最大接触应力为

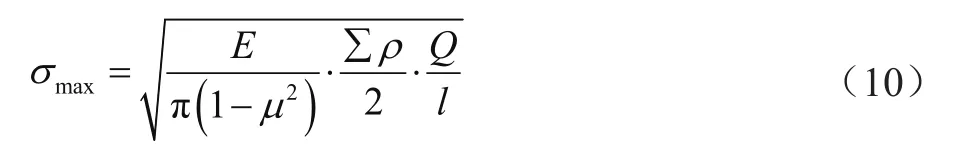
式中：E为弹性模量；μ为泊松比；∑ρ为滚子与滚道线接触的曲率和。

3 结果分析

以某型号三排圆柱滚子轴承为分析对象，三排圆柱滚子轴承主要结构参数如表1所示，模型如图2所示。

图2 三排滚子轴承模型

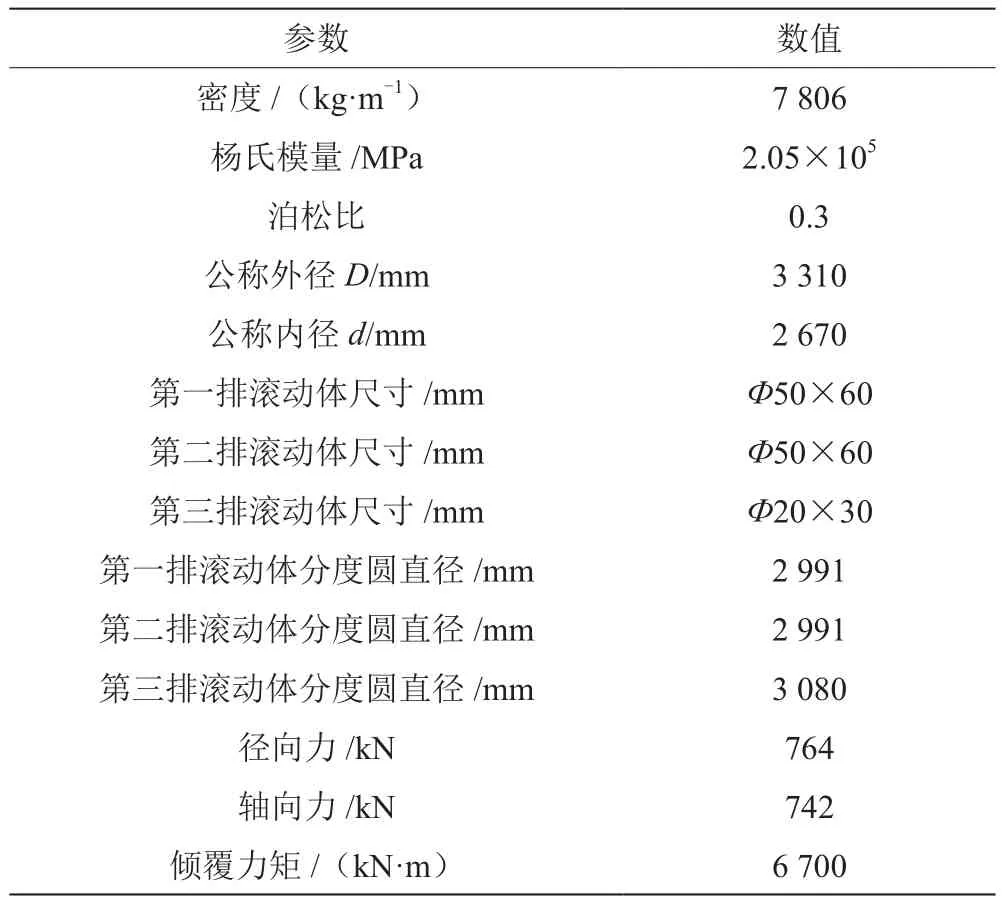
表1 轴承结构参数

3.1 接触载荷分布

按照表1中轴承结构参数和复合载荷，可求得接触载荷Q的分布如图3所示，子载荷分布如表2所示。

由图3和表2可知，第一排滚子最大载荷发生在位置角125.0°处，第二排滚子最大载荷发生在位置角304.5°处。这是因为在倾覆力矩的作用下，第一排滚子与第二排滚子最大载荷发生的位置角相差180°，且在上半内圈范围内倾覆力矩的派生轴向力与外部轴向载荷同向，第二排滚子承受反向的派生轴向力，所以第一排承载滚子数量多于第二排滚子数量。承受径向力的第三排滚子，在位置角307.7°处产生最大接触载荷40.4 kN。

图3 滚动体接触载荷分布

表2 滚子载荷分布表

3.2 应力分布

在表1的复合载荷作用下，三排滚子的最大应力分布如图4所示，三排圆柱轴承内圈滚道应力分布如图5所示。

图4 滚动体最大应力分布

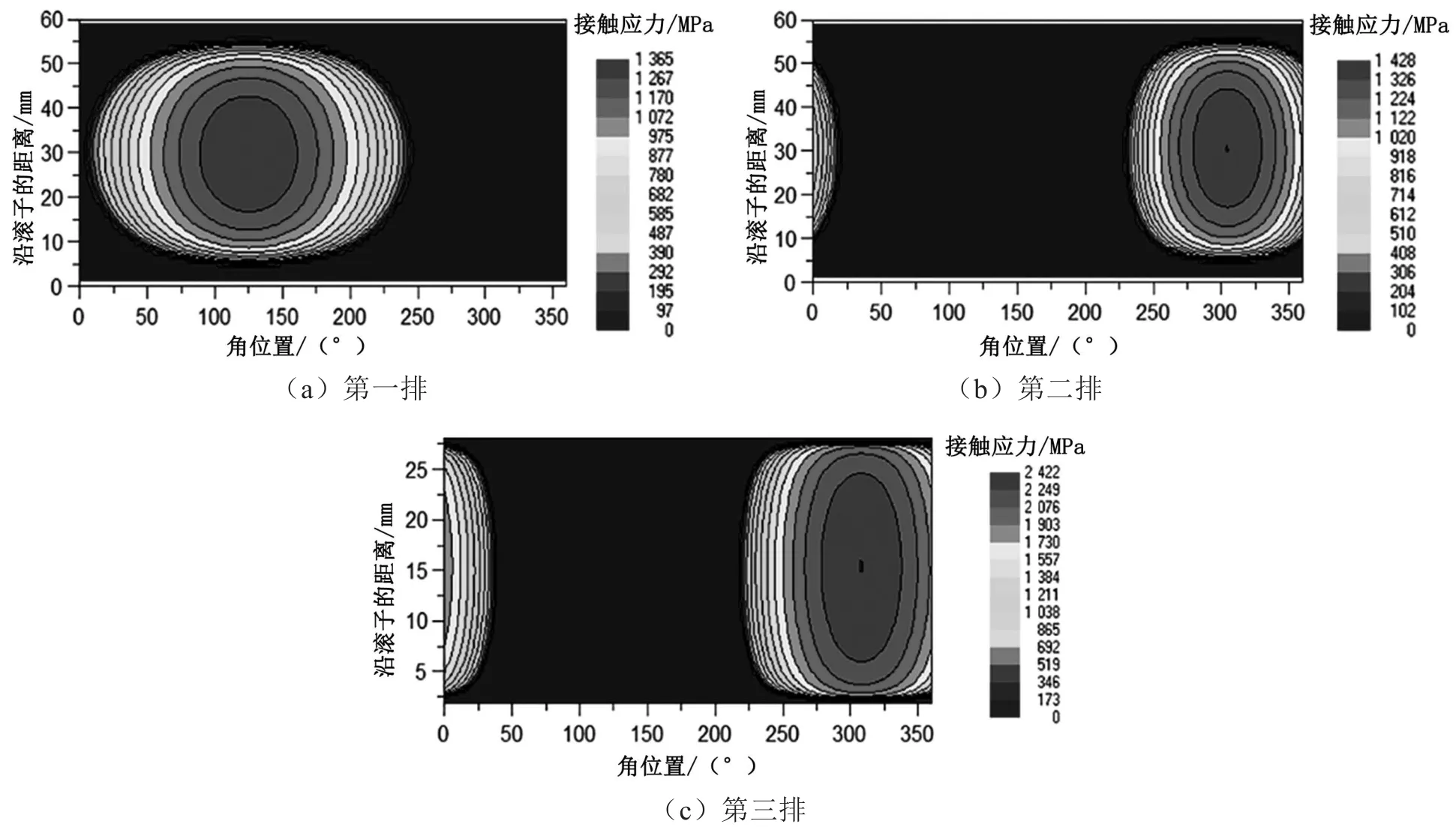
图5 内圈滚道上应力分布图

由图4和图5可知：第一排滚子与滚道最大接触应力为1 364.7 MPa；第二排滚子与滚道最大接触应力为1 428.3 MPa；第三排滚子与滚道最大接触应力为2 422.0 MPa。结合表2分析，第三排滚子承受的最大载荷小于其余两排最大负荷值，而第三排滚子与滚道产生的最大接触应力要远远大于其余两排最大应力值。这是由于第三排滚子的几何参数太小，导致与滚道接触面积过小而引起较高的接触应力。过高的接触应力会导致第三排滚子所处滚道表面率先产生失效，因此在实际生产中可以适当提高第三排滚子的结构尺寸，增大其与滚道的接触面积，避免造成过大的接触应力。图5（a）和图5（b）表明，由于倾覆力矩较大，导致第一排承受载荷的滚子与第二排承受载荷的滚子位于不同侧。

3.3 次表面应力分析

三排圆柱滚子轴承承受载荷复杂且滚子数量多，滚子与滚道接触应力较大，易发生滚道表面剥落，因此研究三排圆柱滚子轴承次表面应力和冯米塞斯应力发生的深度尤为重要。在轴向力为742 kN、径向力为764 kN和倾覆力矩为6 700 kN·m的工况下，三排圆柱滚子轴承内滚道次表面应力分布如图6所示。

从图6可以看出：第一排滚子所接触的内圈滚道最大次表面剪应力为414 MPa，所处深度为0.48 mm；第二排滚子所接触的内圈滚道最大次表面剪应力为433.4 MPa，所处深度为0.5 mm；第三排滚子所接触的内圈滚道最大次表面剪应力为754 MPa，所处深度为0.34 mm。最大滚道冯米塞斯应力如表3所示。可见，适当增加第三排滚子的直径，可减小第三排滚子的接触应力，延长轴承的整体疲劳寿命。

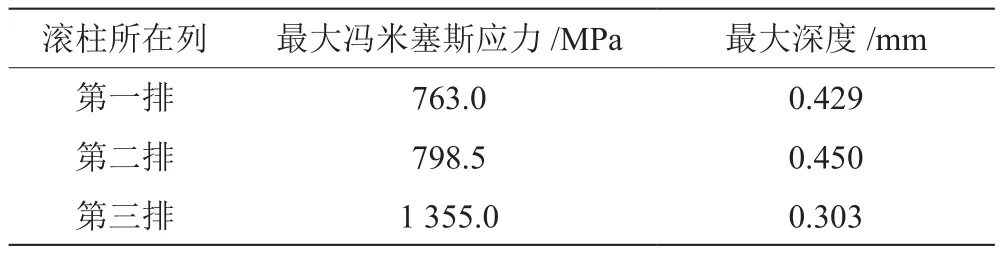
表3 内滚道次表面应力分布

4 结语

建立三排圆柱滚子轴承接触力学模型，计算分析某型号三排圆柱滚子轴承在复合载荷下的接触载荷分布、应力分布以及滚道次表面应力分布，发现第一排、第二排滚子在倾覆力矩的影响下两排载荷分布相差180°左右，且第一排承载滚子数量远远多于第二排承载滚子数量。承受径向力的第三排滚子的接触应力和次表面应力远大于其余两排滚子的应力。适当加大第三排滚子的直径，可以增大滚子与滚道接触面积，减小第三排滚子-滚道表面承受的接触应力和次表面应力，延长轴承疲劳寿命。