射流角度对三角形螺旋夹套传热性能的影响

张 伟，王宗勇，王 超，韩 旭，刘 磊

（沈阳化工大学 机械与动力工程学院，辽宁 沈阳 110000）

换热器作为化工、轻工、石油、动力等许多工业部门中应用最为广泛的设备之一，按传热特征分为直接接触式换热器、蓄热式换热器和间壁式换热器。螺旋夹套是一种间壁式换热装置，与反应釜壁面之间形成传热介质的密封螺旋流动空间，具有结构紧凑和传热高效等优点，被广泛应用于能源动力、化工和石油等领域［1］。流体在螺旋夹套内流动的过程中，会受到夹套结构弯曲和扭曲的共同作用，产生截面二次流，对螺旋主流的温度均化以及对传热边界层的扰动作用增强，传热效果明显强于直管或整体夹套。因此研究螺旋夹套内的换热特性对工程实际应用具有重要意义［2-3］。对于螺旋夹套的传热强化性能研究主要包括三方面内容，也是研究的三个主要阶段，分别为改进结构、加设元件及耦合流动。初期研究，主要侧重于改变螺旋夹套结构（截面尺寸、螺旋半径、螺距）、流体特性（液体、气体、密度、黏度）等，如Dhotre 等［4-5］对层流和湍流条件下冷却液流经半圆管夹套的流动进行了实验研究，建立了半圆管夹套传热系数的关联式；邢云绯等［6］对矩形截面螺旋夹套内的湍流传热特性进行了数值研究，分析了不同入口Re、曲率半径及扭矩等对通道内温度场和速度场的影响；张丽等［7］分析了不同高宽比矩形截面螺旋夹套内的轴向速度、二次流速度、流函数以及涡量的分布规律，实验结果表明，截面高宽比越小时，二次流动越明显，相应的摩擦系数越大；王翠华等［8-9］通过改变三角形螺旋夹套的曲率和挠率对流体流动和换热进行了实验研究和数值模拟，并与半圆管螺旋夹套进行了比较，实验结果表明，三角形螺旋夹套的平均阻力系数（f）比半圆管螺旋夹套小；Zhang 等［10］改变了螺旋夹套的结构，增大壁面波纹度，并与光滑螺旋夹套的传热性能进行了比较，实验结果表明，流动阻力增长幅度小于传热能力增长幅度，总体性能大于1；林清宇等［11］对螺旋夹套内流体流动与传热特性进行了相关研究，在螺旋夹套内加入纳米流体，分析不同基液对螺旋通道流动及传热特性的影响；Gökaslan 等［12］在螺旋夹套内加入不同直径的钢球来进行层流实验研究，给出了压降与修正系数的关联式，并表明螺旋夹套内放置多孔介质会导致压降增加和扰动增强。研究的第二阶段主要侧重于在螺旋夹套内加入各种结构及排列方式的扰流元件（涡流发生器），如陈贵东等［13］在矩形螺旋夹套内加入圆柱绕流元件，对螺旋夹套内局部换热特性进行了数值模拟研究，得到了圆柱绕流元件周围不同螺旋角处的换热效果，且螺旋角约为40°时换热效果最佳；Qing 等［14］以改变螺旋夹套中扰流元件的形状和排列结构为变量来研究不同工况下的流动和传热特性，实验结果表明，组合式的扰流元件比常规结构的强化综合效果提高了40%左右；张丽等［15］在半圆形螺旋夹套内安装三角对翼扰流元件，以研究流动特性，实验结果表明，三角对翼的安装增强了二次流场和流体湍动能。加设扰流元件增加了制造安装的难度，且扰流元件在流体冲击作用下有可能会脱落，进而阻碍螺旋夹套内流体的流动，甚至影响螺旋夹套的正常传热过程。因此，近期有研究者提出了在螺旋流道内加入射流，实现螺旋流和射流耦合流动的强化传热方法，其中李雅侠等［16-18］对圆形截面螺旋管和矩形截面螺旋夹套在加入射流情况下的传热性能进行了研究，分析了射流角度（α）（30°～60°）和射流比对传热性能的影响，实验结果表明，射流的加入明显提高了螺旋夹套的传热性能。

目前，关于射流强化螺旋夹套传热性能的研究处于起步阶段，由于α是影响射流与螺旋主流（横流）流动状态的一个重要参数，因此本工作从该参数入手对三角形螺旋夹套的传热性能进行研究，重新定义α并扩大研究范围（30°～150°），旨在得到α对三角形螺旋夹套传热性能的影响规律，为三角形螺旋流和射流耦合流动的传热理论和结构设计提供参考。

1 数值模拟方法

1.1 物理模型

本工作所研究的三角形螺旋夹套可看做由一等腰直角三角形截面沿着某一圆柱螺旋线转动得到，针对螺旋线和螺旋夹套建立空间直角坐标系O-XYZ，其中OZ轴为螺旋线回转轴（螺旋轴），三角形截面斜边与OZ轴平行，截面斜边中点位于螺旋线上，截面起始位置（螺旋夹套入口）位于XOZ平面内且OX轴通过入口斜边中点，三角形螺旋夹套物理模型如图1a 所示。螺旋夹套的各几何参数为：螺旋半径Rc=165 mm；螺距H=50 mm；螺旋圈数为3 圈（即进出口间螺旋角θio=6π，θ为螺旋角）；直角三角形截面斜边a=34 mm；在距离螺旋夹套入口7π/2 处设置一圆形截面射流管，射流管内直径d=12 mm，射流管与螺旋夹套相对位置关系如图1b 所示。α定义为射流管轴线与三角形螺旋夹套截面直角顶点所在螺旋线切线的夹角。本工作所分析的射流管轴线与螺旋线相交，且始终处于螺旋线在交点处的密切平面内，本工作所研究的角度范围为α=30°～150°。

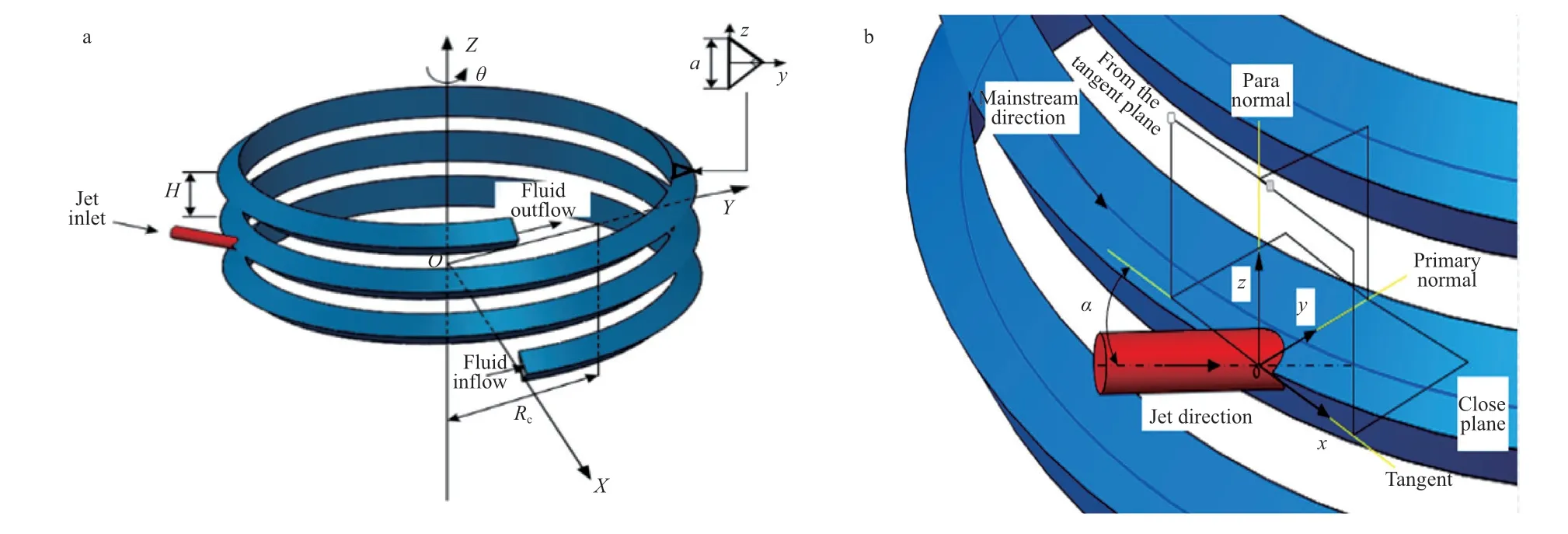
图1 带有射流管的三角形螺旋夹套物理模型（a）及射流管与螺旋夹套相对位置（b）Fig.1 Physical model of triangular spiral jacket with jet tube(a) and relative position of jet tube and spiral jacket(b).

1.2 数学模型

射流和螺旋流均以相同条件下的不可压缩流体——水为工作介质。因为Realizablek-ε模型适用于旋转流动、强逆压梯度的边界层流动、流动分离和二次流等，特别是射流曲率变化大的情况下有很好的表现［19］，故采用Realizablek-ε湍流模型，对加入射流管的等腰直角三角形螺旋夹套内流体的三维稳态湍流流动与换热进行数值模拟，并结合时均控制方程和能量方程对数据进行处理［20］。

1.3 数值模拟方法及边界条件

采用CFD 软件的Fluent 模型进行数值模拟，螺旋夹套主流入口和射流管入口均采用速度入口，入口水温均为293 K，螺旋夹套出口为充分发展出口。根据Srinivasan［21］提出的螺旋夹套临界Re（Recr）表达式可知，在本工作螺旋夹套结构参数下Recr=6 386，本工作所研究的Re范围为9 000～12 000，在该范围内流体已进入湍流状态。设置螺旋夹套内壁面为受热面，受热面为恒温边界条件，恒定壁温为373 K。将螺旋夹套进出口间流体的平均温度作为工质的定性温度，工质的物性参数（ρ，Cp，λ，μ）以工质的平均温度为参考而确定。压力-速度耦合采用SIMPLEC 算法，二阶压力离散，动量、湍动能、湍流耗散率、能量方程均采用二阶迎风离散，能量方程收敛残差设置为10-6，其余收敛残差均设置为10-4。

1.4 网格独立性验证

数值模拟网格采用结构化网格，并对传热壁面边界区域、射流管与螺旋夹套交接处进行了网格加密，如图2 所示。为了消除网格尺寸对计算结果的影响，提高计算结果的可靠性和准确性，本工作采用5 套网格对研究对象在流动和结构参数相同情况下（α=45°、螺旋夹套当量直径与射流管直径的比值dh/d=1.17、螺旋主流Re=10 000）的传热性能进行模拟计算。图3 为网格独立性验证。结合图2和图3 可知不同网格数量下螺旋夹套平均努塞尔数（Num）和f的变化情况。当网格数量较少时，Num和f产生较大幅度的变化，整体趋势是随着网格数目的增加而增加，当网格数量达到311 万以后，Num和f基本保持不变，为了兼顾数值模拟的准确性以及计算时间，本工作选取311 万左右的网格数量进行数值模拟，网格最大节点间距为1.1 mm。

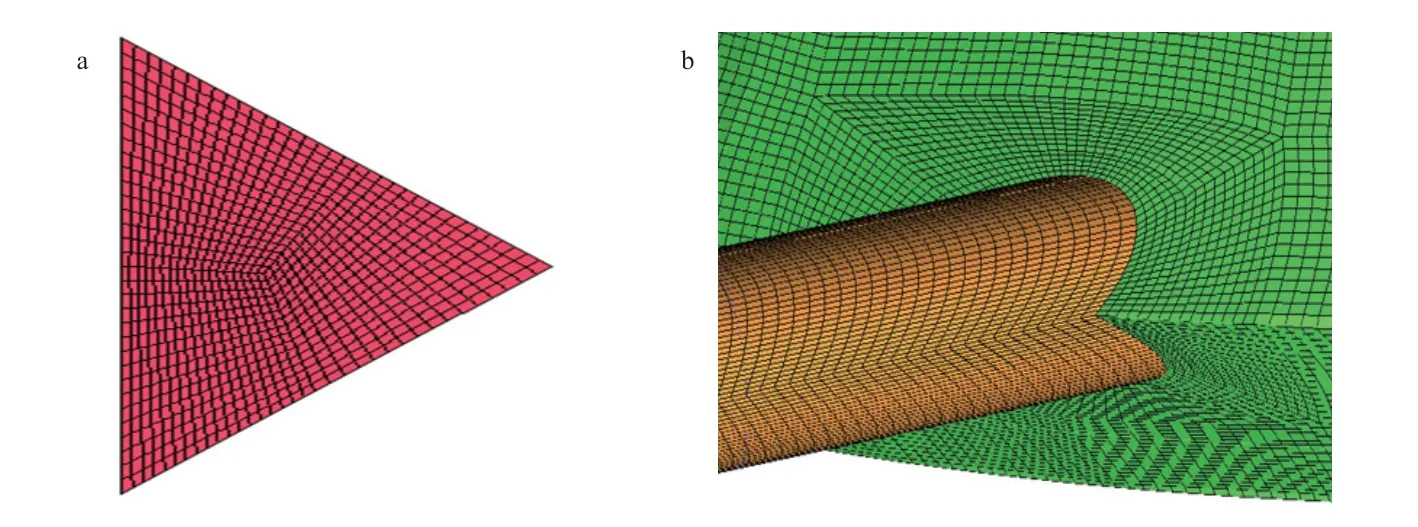
图2 三角形截面（a）及射流管与螺旋夹套交接处（b）的网格Fig.2 Mesh of triangular cross-section(a) and the junction of jet tube and spiral jacket(b).

图3 网格独立性验证Fig.3 Mesh independence validation.

1.5 模拟结果验证

为了验证数值模拟结果的准确性，本工作分别对不带射流管的单一螺旋夹套和带有射流管的螺旋夹套进行了数值模拟，并在工质及结构参数相同的情况下与文献［22］进行了对比，结果见图4。由图4 可知，这三种数值模拟结果中的Num随着Re的增大有着相似的变化规律。而且单一螺旋夹套的数值模拟结果中Num和文献值的最大偏差在5.1%左右，验证了该数值模拟的准确性。

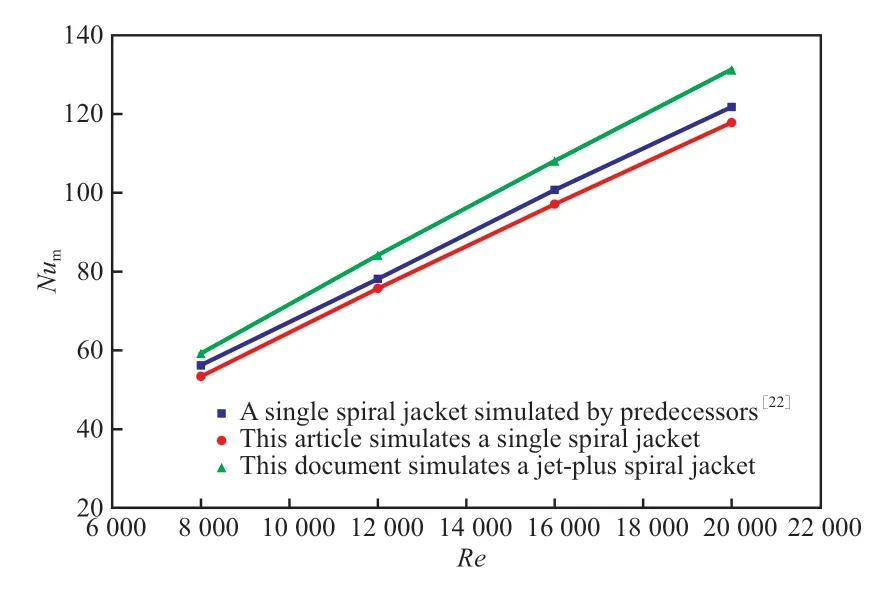
图4 数值模拟结果验证Fig.4 Numerical simulation results validation.

2 结果与讨论

2.1 螺旋截面速度分布变化分析

流体在螺旋夹套入口段和射流影响区域都有较大的速度波动，已有的传热理论及研究结果均表明速度变化对于传热具有直接影响，为了揭示夹套横截面速度分布沿螺旋轴线（相对螺旋角γ=θ/θio）的变化情况，定义相邻截面的速度方差（σ）为：

式中，vhi为后面截面（分析截面）某点速度，m/s；vqi为相邻前面截面某点（与后面截面是同一点）速度，m/s；n为截面上所取速度点的个数。

图5 为螺旋夹套截面σ随γ的变化情况。由图5 可知，从进口处到γ=0.200，σ呈现先上升后下降的变化趋势，这说明流体均匀流进入口后速度分布的差异快速增大，在γ=0.080 处σ达到最大值，之后以相对缓慢的速度下降，在γ=0.200 位置（即θ=3π/2）处接近于0，说明在该流动长度范围内螺旋流处于未充分发展段；而γ=0.200～0.543 范围内σ始终处于极低水平，说明螺旋流处于充分发展状态；当γ≥0.543 后，σ呈现快速上升趋势，在γ=0.583（射流安装位置）处达到最大值，而后进入下降阶段，在γ=0.900 处σ再次趋近于0，说明在γ=0.543～0.900 范围为射流的影响区域，该长度占螺旋夹套总长的35%，说明射流对螺旋流速度分布的影响很大，而射流对传热的影响长度范围有待后面进一步分析。在γ=0.900～1.000 范围，螺旋流再次进入充分发展的恒定流动阶段，加上入口附近的恒定流动段，在整个流道长度范围内充分发展流长度约占总长的28%。

图5 螺旋夹套不同截面位置处的σFig.5 Velocity variance(σ) at different cross sectional positions of the spiral jacket.

2.2 阻力系数分析

图6 为不同α下f随着Re的变化趋势。由图6 可知，不同α的螺旋夹套以及单一螺旋夹套内f均随着Re的增大而下降，这是由阻力系数定义决定的，也就是阻力系数与速度成一定的反比关系，是流动的一种基本规律。纵向观察图中各条曲线可知，单一螺旋夹套将各角度射流夹套分成两部分：当α=90°～150°范围时，射流夹套f高于单一夹套f；当α=60°时两者已经比较接近，特别是相同的Re下还略有降低；当30°≤α≤45°时射流夹套的f要小于单一夹套f，但相差不大。产生这种现象的原因是：射流以较高的流速射入螺旋夹套后会对螺旋流产生卷吸作用，同时也会对壁面产生冲击作用，此外射流的核心区对螺旋流还有产生阻流绕流作用。当90°＜α≤150°范围时，射流与螺旋流整体呈逆流状态，随着角度的增大，尽管对壁面的冲击作用有所降低，但射流的阻流作用显著增大，导致f上升；当α=90°左右时，射流与螺旋流呈错流状态，射流对壁面的冲击作用最强，对螺旋流的阻流作用也比较大，致使f也处于一个较高水平；当30°≤α＜90°时，射流与螺旋流整体成并流状态，除了上述的能量消耗因素之外，射流对螺旋流还具有一定的推动作用，当α=60°左右时，射流对流体的正反两方面作用达到一种平衡状态，因而f与单一螺旋夹套f接近，而当30°≤α≤45°时射流对流体推动作用超过了对流体的阻碍作用，所以f小于单一夹套f。

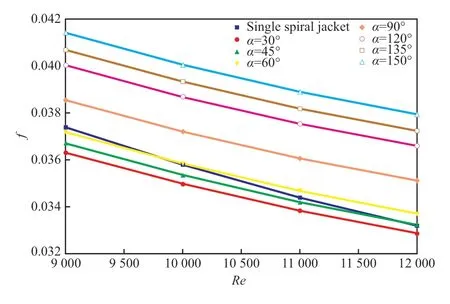
图6 不同α 下f 随Re 的变化关系Fig.6 Relationship between f and Re at different α.

基于图6 的模拟结果，拟合出f的关联式，见式（2）。

适用范围为9 000 ≤Re≤12 000，30°≤α≤150°，拟合点处的最大误差不超过2%，拟合的相关系数（R2）为0.96。

2.3 传热特性分析

为了分析传热与速度之间的关系，绘制了不同螺旋角度下螺旋夹套截面努塞尔数（轴向截面努塞尔数（Nua））变化曲线，见图7。对比图7 和图5 可知，Nua与σ存在着相似的变化规律。当γ≤0.200 时，传热也处于非充分发展阶段，传热边界层逐渐增厚，传热效果变差；当γ=0.200～0.543范围时，传热与流动同步进入到充分发展阶段，在该阶段Nua处于较低水平；当γ=0.543～0.700 范围时，由于射流作用，Nua相比上游充分发展段显著增大，先升后降，在射流入射位置达到最大值，之后进入下降阶段，直到γ=0.700 开始进入变化较小的平稳阶段，但该阶段的Nua也明显高于射流入射点上游的传热充分发展段，约高30%，说明γ=0.543～1.000 范围均是射流强化传热的影响区域，占夹套总长的45%，高于射流对速度分布的影响范围。因此，流动与传热具有良好的协同关系，速度差别增大有利于提高传热性能。

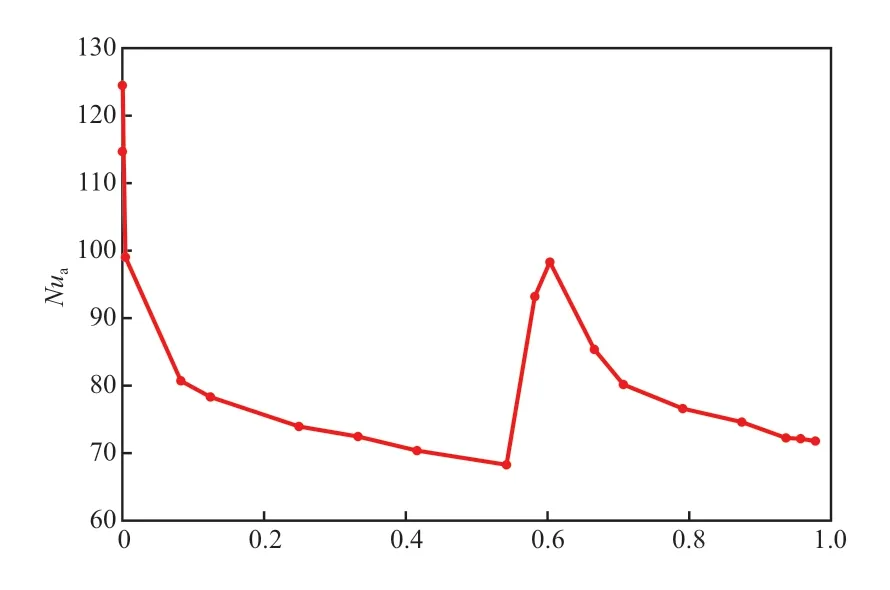
图7 Nua 随截面位置的变化Fig.7 Change of axial local Nussell number(Nua) with cross-section position.

图8 为不同α下螺旋夹套的Num随Re的变化关系。由图8 可知，Num均随着Re的增大而增大，且加入射流的螺旋夹套的Num要远大于单一螺旋夹套的Num。在所研究的Re范围内至少提高10.5%。对比不同α下的Num曲线可知，随着α的不断增大，Num也相应增大，只不过增大幅度相对较小，α=150°与α=30°相比提升7%左右。产生这种变化的原因为：当α≤90°时，随着α的增大射流对壁面的冲击作用增加，传热边界层减薄；而当α＞90°时，虽然射流对传热壁面的直接冲击强度有所削弱，但是由于与螺旋流呈逆流状态，近壁面回流区域随α的增大而增大，致使传热边界减薄、扰动程度增强，该增强程度超过冲击削弱程度，因而在整个α范围，均表现为α增大，Num提高。

图8 不同α 下Num 随Re 的变化关系Fig.8 Relationship between Num and Re at different α.

根据Num随Re和α变化的模拟结果，拟合出Num的关联式，见式（3）。

适用范围为9 000 ≤Re≤12 000，30°≤α≤150°，拟合点处的最大误差不超过1%，拟合的R2为0.996。

为了进一步揭示射流对螺旋夹套内壁面换热的强化作用，研究了传热壁面不同径向位置局部努塞尔数（径向局部努塞尔数（Nuc））随局部相对坐标z/a的变化情况（Re=10 000，α=π/4），见图9。由图9 可知，不同截面处的Nuc都呈现了两边高中心略低的现象，γ=0.300（射流管之前）处的Nuc整体低于其他螺旋位置曲线，说明传热壁面整个长度均得到了射流的强化。射流入射截面位置（γ=0.583）处的Nuc远大于上游γ=0.300 处，随着截面位置逐渐向下游移动，Nuc逐渐减小至稳定数值，但也明显高于射流入射点上游。对比不同径向位置，可见三角形截面斜边角点附近传热效果较好，优于中心范围。形成这种差别的原因为：射流冲击到壁面后，向两侧分流形成二次流，由于越靠近角点流动面积越小，流速会相应增大，导致角点附近传热增强；角点和中心区域Nuc大小关系主要取决于射流比，当射流比增大后中心区域Nuc会进一步增强，二次流向对称轴方向靠拢，中心区域的Nuc会高于角点区域。

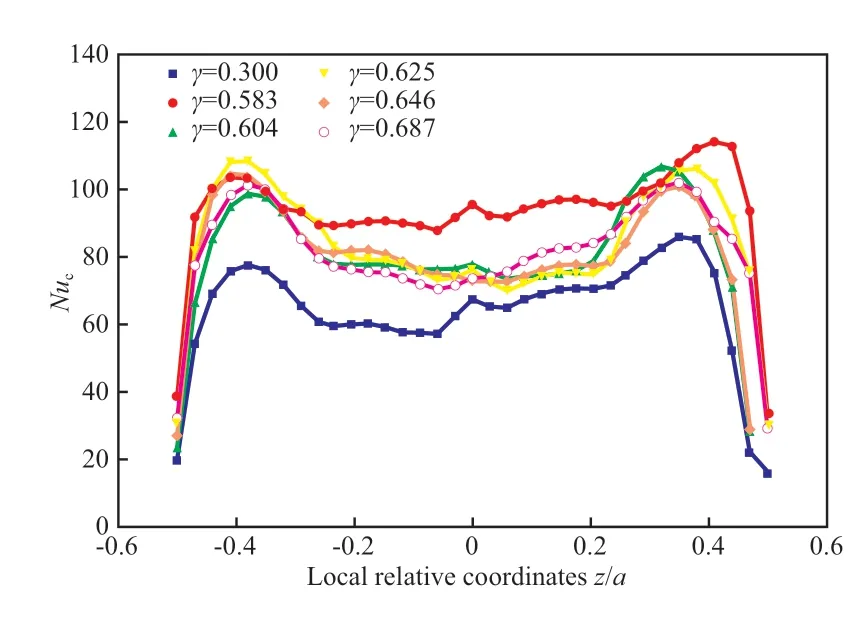
图9 Nuc 随不同截面位置的变化关系Fig.9 Variation of radial local Nusselt number(Nuc) with different section positions.

2.4 综合强化传热性能的分析

射流管在三角形螺旋夹套外壁安装，在增大螺旋夹套内壁面的换热效果的同时，也会使流动阻力相应增加。为了综合分析传热效果和流动阻力情况下的相对传热效果，引进传热性能综合评价因子（PEC）来表征加入射流后的螺旋夹套传热性能［23］。

式中，Nu0m为无射流螺旋夹套内壁面换热的平均努塞尔数；f0为无射流螺旋夹套内的平均阻力系数。

图10 为不同α下PEC 随Re的变化关系。由图10 可知，任一角度的PEC 均随着Re的增大而增大，且增大趋势基本一致。在Re一定的情况下，α=30°～135°时，PEC 随着α的增大而下降，原因为射流与主流汇合后会增强主流的径向速度，使其对内壁面边界层的冲刷更为剧烈，α越大这种效果越强，内壁面换热也就越强，但随之带来的是射流对主流轴向速度的抑制，使阻力也越来越大，射流与主流交汇处会出现部分区域的流体速度急剧下降的现象，阻力增加的幅度超过了努塞尔数的增加幅度，故PEC 下降。而α=135°～150°时PEC 上升的原因是由于α的增大，射流对壁面的冲击作用虽然有所减弱，但射流使近壁面区域的回流区域明显增大，对传热边界层的扰动显著增强，流体阻力增大的程度小于Num增大的程度，故出现PEC 上升现象。可以明显看到α=30°～45°的PEC 相差不大，比其他角度好。因此，从综合传热性能角度，α=30°～45°对于三角形螺旋夹套是一种比较好的选择。

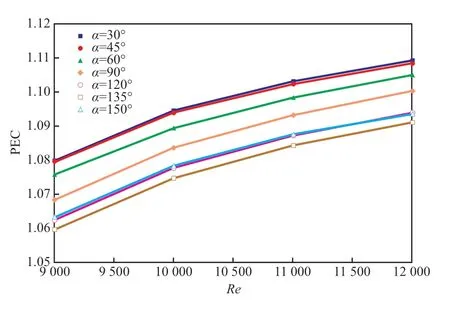
图10 不同α 下PEC 随Re 的变化关系Fig.10 Relationship between PEC and Re at different α.

3 结论

1）在所研究的Re范围内，Num和f均随着α的增大而增大，Num和f与Re和α的拟合关系分别为：Num=0.163 02Re0.65886α0.0181和f=0.502 53Re-0.32472α0.08954。

2）三角形螺旋夹套内流速分布与传热效果存在良好的匹配关系，σ较大截面的传热效果较好，即Nua正比于σ，在γ=0.543～0.700 范围内Nua增大明显，最大Nua相比Num提升了30%，而射流对速度和传热的影响区域范围分别占夹套总长的35%和45%。

3）射流强化了Nuc，斜边角点及中心部位增加尤为明显，Nuc沿竖直壁面呈现两端及中心高的分布特点。

4）PEC 随着α的增大呈现先下降（α=30°～135°）后上升（α=135°～150°）的变化规律，α=30°～45°范围内PEC 接近，且PEC 最高。从综合性能角度而言，α=30°～45°对于三角形螺旋夹套是一种比较好的选择。