“数与代数”领域五年级学生几何直观测评分析——以重庆市江津区学业质量监测试题为例

重庆市江津区滨江四牌坊小学校（402260）郑华恒

重庆市江津区鼎山小学校（402260）唐 静

几何直观，即运用图表描述和分析问题的意识与习惯。“数与代数”领域占据小学数学课程内容的半壁江山，在发展学生几何直观中起着重要作用。下面将通过观察学生在“数与代数”领域运用几何直观解决实际问题的真实表现，了解学生几何直观发展状况，为发展学生几何直观提供参考，进而实现学生深度的“学”与教师深度的“教”。

一、几何直观：一种重要的数学素养

检索《义务教育数学课程标准（2022年版）》（以下简称“2022年版课标”），“几何直观”出现了48次。同时，几何直观也是众多学者重点关注的研究对象，表1是一些学者关于几何直观的代表性观点。

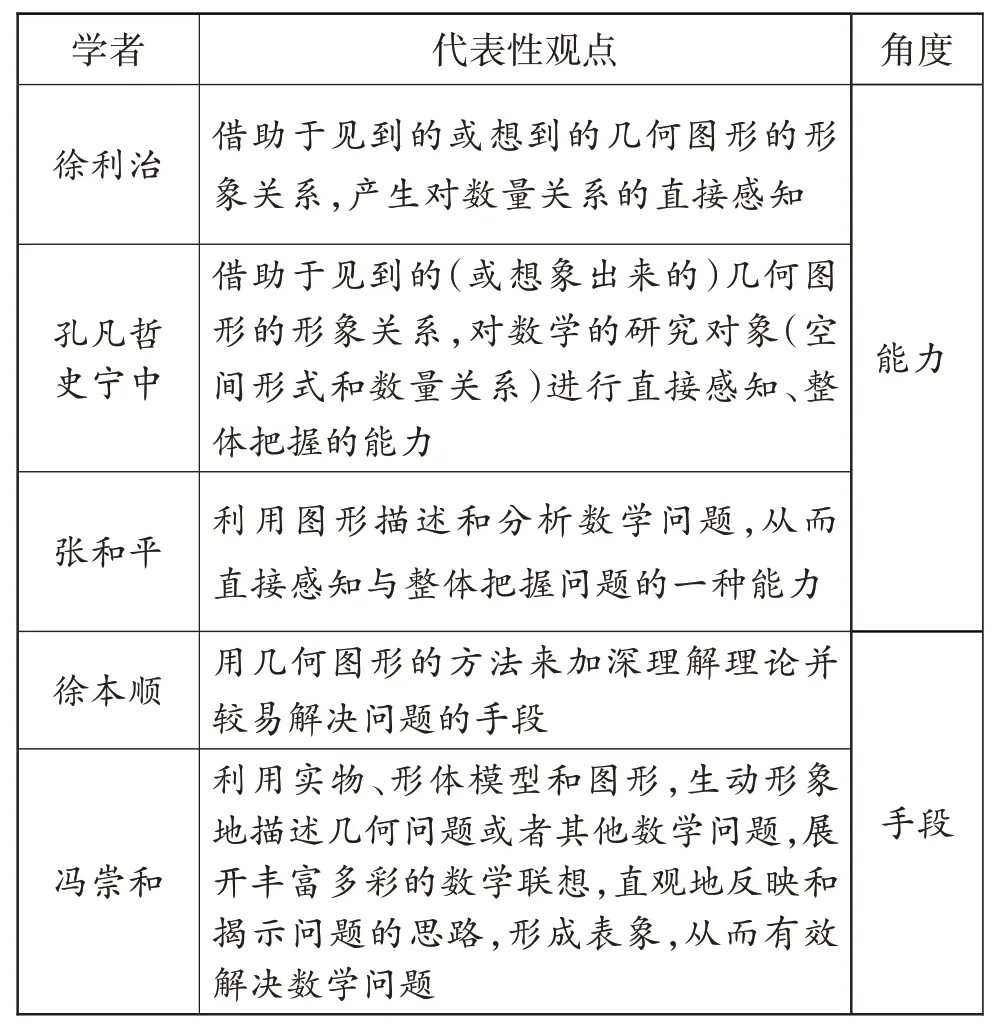
表1 学者关于几何直观的代表性观点

续表

几何直观主要有两层含义：一是用数代形；二是以形助数。在“数与代数”领域，几何直观将数的概念的建立、数的运算的算理及算法形象化，将问题解决的思路可视化，帮助学生深刻理解数学的本质。比如，教师常常借助数线模型引导学生强化整数、小数、分数等数的概念的理解；借助面积模型帮助学生理解整数乘除、分数乘除等算理及算法。在“数与代数”领域，考查学生的几何直观有三个方面：一是能否借助几何直观理解数学概念，二是能否借助几何直观描述和分析数的运算，三是能否借助几何直观寻找解决问题的思路。

二、原题重现：学生画得怎样？

2022年重庆市江津区五年级学生学业质量监测试卷中有这样一道题（如图1）：

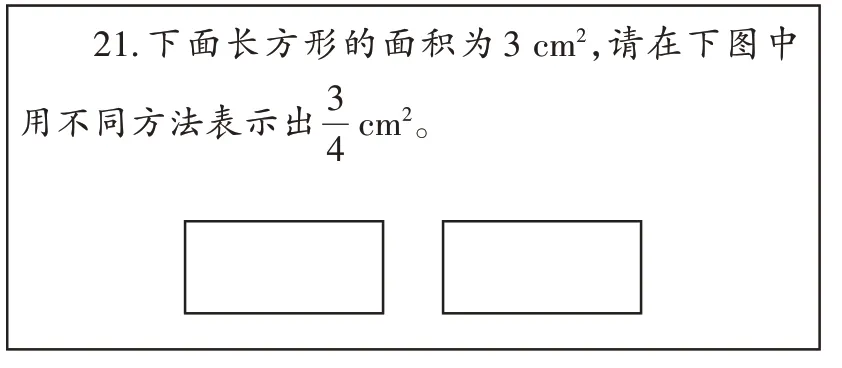
图1

1.分数的教学要求

分数概念是高年段“数与运算”的重要内容，2022年版课标在第三学段“数与运算”中提出了如下部分要求：一是内容要求，结合具体情境探索并理解小数和分数的意义，感悟计数单位；二是学业要求，能用直观的方式表示分数和小数；三是教学提示，在初步认识小数和分数的基础上，引导学生在具体情境中，理解小数和分数的意义，感悟计数单位。

2.整体完成情况

2022年重庆市江津区五年级共7426名学生参加了测评，总体情况如表2所示。

全卷与本题区分度都高于0.4，区分度较好；相比全卷而言，本题在难度上偏大，但还在学生可接受范围内，用于考查五年级学生几何直观素养是可行的。

3.不同层次的学生表现

有83.14%的学生是用了基本做法（如图2），他们的解题思路大致为：把理解为3cm2的即把3cm2的长方形平均分成4份，借助除法“3除以4”画出图形。

图2

有58.04%的学生有不一样的做法（如图3），他

图3

有12.04%的学生完全做错，或者根本就不会做。更值得关注的是，就作图效果上看，学生大多不用工具（直尺、铅笔等），图形不规范的现象较为普遍。

三、影响因素：学生的学习障碍在哪？

1.数与代数的特殊性导致直观表达困难

已有研究表明，学生的几何直观在课程内容上的表现差异较大。西南大学张和平对1093名小学生进行测查分析，发现小学生在“图形与几何”“统计与概率”领域表现较好，在“数与代数”领域表现较差。河北科技师范学院曹现榆通过实证研究也发现，学生在“图形与几何”领域得分率为0.81，在“统计与概率”领域得分率为0.73，而在“数与代数”领域的得分率仅为0.46。在实际的课堂教学中，大多数教师认为发展学生几何直观能力更多的是在“图形与几何”领域，而忽视在“数与代数”领域中进行渗透。殊不知，“数与代数”课程内容的学习更强调逐步抽象、理解算理算法、推理验证。

学生在上述测试题中表现不佳，跟分数本身的抽象性和复杂性有关。受限于教材给出的定义“把单位‘1’平均分成若干份，表示这样的一份或几份的数，叫作分数”，学生的学习倾向于强调对单一整体作为单位“1”的认识，忽视对集合整体作为单位“1”的认识；教师的教学倾向于强调理解教材给定的概念，而忽视分数与除法的关系教学。因此，部分学生在做监测试卷第21题时惯性默认长方形为单位“1”，将其平均分成4份，涂了其中的3份；部分学生不能很好地将分数与除法建立联系，因此不能想到图3的画法。在实际教学中，学生直观表示假分数也有困难。比如，学生由于无法将数轴上的0～2合并看成单位“1”，就认为在数轴0～2内无法表示出；当要求用圆表示时，学生因为不能理解要利用两个同样大小的圆来表示，而感到束手无策。

2.学业测评的滞后导致学与教动力不足

相对而言，几何直观在“数与代数”领域的测评还未引起重视。几何直观测试题更多是分布在“图形与几何”和“统计与概率”领域，“数与代数”领域安排过少。加之，基层学校苦于没有科学有效的测评工具，缺乏可靠、合理和多样的几何直观测评题目，造成几何直观测评难以开展。测试题大多基于简单思维的“读懂图”，而不是高阶思维的“作出图”。比如，根据图示写算式的多，而根据算式画图的少；根据线段图分析数量关系的多，而根据问题情境画图分析数量关系的少。几何直观的测评相对滞后导致学与教动力不足，使“数与代数”领域对学生几何直观的发展作用未能很好发挥。

又如，分数概念的测试更多的是这类形式的填空题：把3米长的彩带平均分成4段，每段占全长的（），每段长（）米。

这样的填空题考查学生对具体情境中分数不同意义的理解，是比较好的典型试题，应该继续保留。2022年重庆市江津区五年级学生学业质量监测试卷第21题的样态，不仅是题型的改变，更是一种对几何直观素养的倡导。从后续的师生访谈上看，这样的改变受到了师生的普遍欢迎，学生认为“更有意思”“更有挑战”，教师认为“更能考出真实水平”“更能综合呈现学生的数学学习水平”“更能可视化地展现学生对分数意义的理解”。

3.读图与作图的失衡导致几何直观能力较弱

会读图与能作图，是学生几何直观的重要表现。读图是作图的基础，作图是读图的进一步发展；作图能力也会在更深层次上影响读图能力的发展；读图与作图能力协调发展更有利于学生几何直观能力的提升。学生目前的情况是读图与作图“两条腿”的步调并不一致，形成的原因有以下两个方面。

一方面，将图表局限于“辅佐”地位。教材在数的概念理解、算理解读、问题解决中有大量的直观图表，使学生对图表大多停留在“读懂”阶段，只通过“读懂”图表理解知识、突破难点。学生用眼观察多，动手实践少，导致独立作图、列表分析的能力较弱。另一方面，忽视作图规范。学生作图随意、不规范、不严谨，作图水平不高、效果不佳。

由此就引发了一系列问题，如虽然教师引导学生“画一画更清楚”，但学生仍然很少主动提笔作画。在学生心里，作图是“图形与几何”的事，列表是“统计与概率”的事，“数与代数”就不用凑热闹了；学生还认为，作图是“老师教的手段”，而不是“我要学到的方法”。教师知道画图、列表是一项重要的学习能力，也希望学生动手画图、列表，但在课堂实践中却没有很好地落实，在课内与课外也没有很好地设计画图或列表的作业。这就正如特级教师刘善娜所说，我们要的是“图”的效用，缺的却是“画”的能力训练。

四、改进策略：“数与代数”领域发展学生几何直观的可能路径

“数与代数”是发展学生几何直观的重要载体，但学生在此领域的表现较差。在“数与代数”领域发展学生的几何直观，除了要夯实数与运算、数量关系等基础知识，还应在理念更新、教材编写、课堂教学、作业设计、评价改进等方面协同努力。

1.理念更新：认识到几何直观对于学习的多重意义

直观，是数学发现的先导，也是学生先天具有的学习潜质。几何直观不仅是一种能力，更是学生学习数学的一种思维方式。以“数与代数”课程内容为载体，发展学生几何直观，应该以呵护学生先天的直观潜质为起点，以后天有效提升几何直观素养为方向，促进学生达到“用形象思维洞察”的高阶水平。在培养策略上，加强读图、作图教学，比如，通过数形结合建立形与数的联系，利用图表来直观理解数的概念和运算，分析数量关系，刻画变量间的复杂关系，探索解决问题的思路，厘清思维路径，构建数学问题的直观模型，等等。因此，教师要强化数形结合，丰富学生观察、操作、想象、推理、表达等数学活动，注重技能训练，使学生逐步养成画图、列表等习惯。

2.教材编写：为学生提供更多直观表达的机会

教师可适量增加教材例题的动态作图过程，统筹呈现读图与作图，即对教材上静态的直观图表，教师要化静为动，以此引导学生感悟直观表达的过程。图4展示的是教材例题及其对应的课堂活动，是一个比较好的范例。

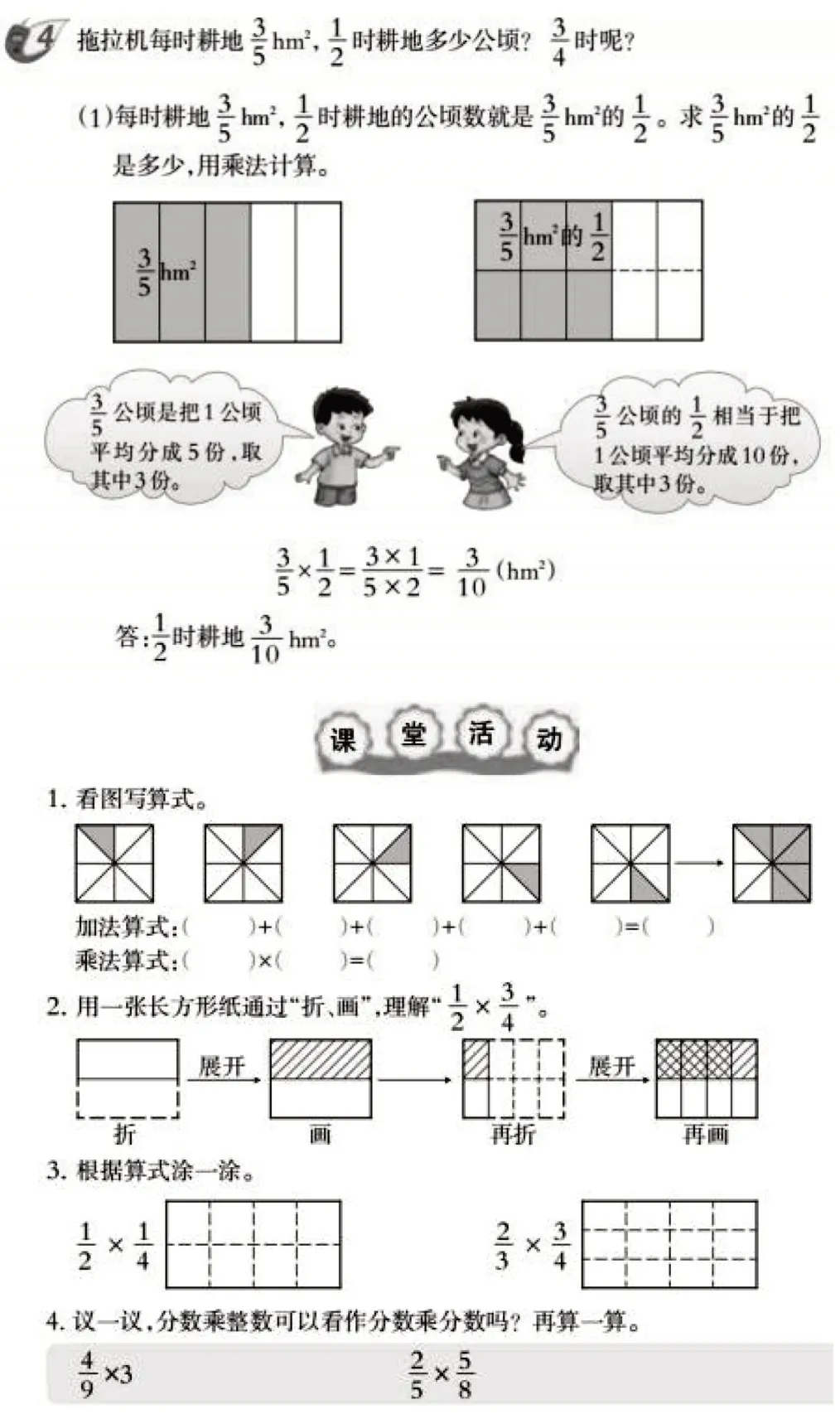
图4

教材的例题是用面积模型直观呈现问题情景，两幅连续的图和不同的色块动态显示两次平均分的过程，帮助学生理解分数乘分数的算理；“课堂活动”的第2题和第3题是让学生用“折”“画”“涂”等实践性操作进一步直观理解分数乘分数的算理。教材的例题与课堂活动互相呼应，体现了学生学练一致性。

3.课堂实践：给予直观表达足够的时空

课堂教学是发展学生几何直观的重要阵地。积极解决“课时太紧张，没时间去探究”“怎样的学习材料更直观”“培养学生作图有何技巧”等现实问题，就显得很有意义。首先，加强区县教研和校本研讨。整理并分析几何直观在“数与代数”领域各年级教材中的体现，有针对性地渗透几何直观；整合学科内容，灵活调配内部课时，增补相应的读图、作图等重要的几何直观内容。其次，加强自我实践与课例研讨。教师要进行几何直观典型课例研究，并分享几何直观教与学两个层面的经验。最后，发挥几何直观优势，营造直观表达的学习环境。展示学生的不同作品，解析优秀作品“好在哪里”，指出缺陷作品“哪里要改”，激励学生主动采取几何直观的方式去处理真实的数学问题。

4.作业设计：从读图走向作图

作业是学生自主发展几何直观的实践载体。设计作业时要给学生增加“画数学”的机会，如习题从单一的列式计算走向丰富的直观分析；引导学生从习惯读图走向习惯作图，促进思维可视化。为体现几何直观的进阶性，在不同学段可对学生有不同的要求：第一学段，作图表达简单的数量关系，以及认数、认识时间，感悟数量关系，增强数感和时间感；第二学段，作图表征分数、小数及其大小比较，用图示表征题意，厘清四则运算的关系，巩固积、商的变化规律；第三学段，聚焦分数、百分数概念的理解及其难题的分析，如画线段图表征分段计费，用面积模型表征分数乘除法算理，用思维导图表征主题单元内容体系，等等。

5.评价导向：科学设置测评内容

几何直观是学业测评的重要内容。根据2022年版课标中的“学业要求”和“教学要求”，科学设置测评内容能有效促进教师改进教学和落实学生深度学习的发生。“数与代数”领域关于小学生几何直观测评包括“数与运算”“数量关系”两大主题；用图示或符号来表示整数、分数、小数的意义及其大小比较；用图示表示数的运算；读懂图示并列出算式；会画图或列表分析较复杂的问题情境，解决生活中碰到的数学问题。下面给出3道测试题供大家参考（如图5）。

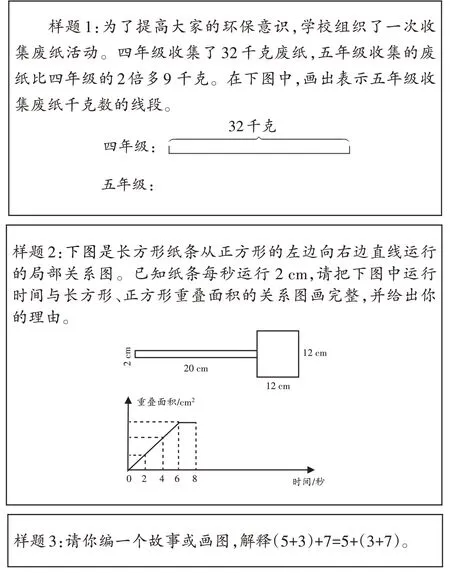
图5

综上所述，“数与代数”领域发展学生几何直观有着其特殊的意义与作用。教师要精选或改编“数与代数”领域的课程内容，丰富学生几何直观数学活动经验，强化作图、列表的技能训练，帮助学生既能读图，又会作图。如此，学生几何直观在“数与代数”领域才有长足的发展。