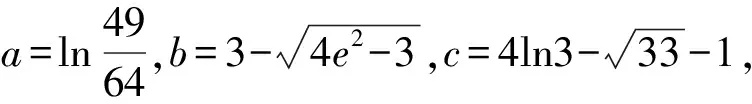2022年高考“比较大小”题目归类及解法

耿 永

(贵州省遵义市第十八中学 563099)

2022年全国甲卷理科第12题、2022年全国甲卷文科第12题涉及到的解法有作商法、三角不等式法、找中间值法、构造函数法及高等数学中的泰勒展开式放缩等，现就这两题给出部分解法。

A.c>b>aB.b>a>cC.a>b>cD.a>c>b

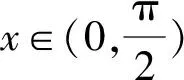
则F′(x)=f(x)=sinx-x<0.

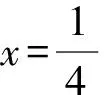
所以b>a.

综上,c>b>a.故选A

对于函数f(x)=cosx在x0=0处有

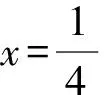
所以b>a.

例2(2022年全国甲卷文科第12题)已知9m=10,a=10m-11,b=8m-9，则( ).

A.a>0>bB.a>b>0 C.b>a>0 D.b>0>a

解法1 由选项知：可找中间值法,取中间值0.

若a>0，则10m-11>0.

即10m>11，m>lg11.

由9m=10,得m=log910.

所以log910>lg11.

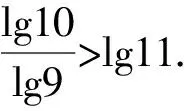
即lg10>lg9·lg11.

所以a>0成立.

若b<0，则8m-9<0.

即8m<9.

即m

由9m=10,得m=log910.

所以log910

即lg8·lg10<(lg9)2.

所以b<0成立.

综上,a>0>b.故选A.

解法2 由a=10m-11=10m-10-1，

b=8m-9=8m-8-1,

可构造函数f(x)=xm-x-1，

此时a=f(10)，b=f(8).

而f(9)=9m-9-1=9m-10=0,

又f′(x)=mxm-1-1，

由f′(x)=0，得mxm-1=1.

如图1所示,a=f(10)>0，b=f(8)<0.

图1

综上,a>0>b.故选A.

通过对2022年高考比较大小题目的解法可知：要想在短时间内准确解答此类题型，必须熟练掌握相应方法，同时对一些常用的放缩，如：ex≥x+1(当且仅当x=0时等号成立)；lnx≤x-1(当且仅当x=1时等号成立)，并在具体题目中归类整理，熟记一些二级结论及其变形公式，对解答此类题目都有很大帮助.

A.a

A.a

练习3 已知a=810,b=99,c=108,则a,b,c的大小关系为( ).

A.b>c.aB.b>a>cC.a>c>bD.a>b>c