人为坑洞对运营铁路路基稳定性的影响

袁万军

(中国铁路北京局集团有限公司，北京 100038)

1 概述

人为坑洞是指线路所经区域存在的废弃防空洞、菜窖等人为开挖的洞穴，这些坑洞位于地下，洞口大多被掩埋，难以直接发现，需采用多种物探方法才能准确判别位置[1]。铁路线路以路基形式通过后，受铁路荷载以及土遇水饱和后力学参数降低的影响会造成洞穴坍塌，引起路基沉降，影响行车安全。

目前，坑洞对铁路路基稳定性影响的评价方法主要有岩溶顶板稳定评价中的荷载传递交汇法[2]、顶板坍塌自行填塞法、抗弯抗剪结构力学分析法(岩石地层)、极限平衡条件抗剪验算法(岩石地层)、厚跨比法(岩石地层)[3]，以及采空区稳定性评价中的荷载临界深度判别法、附加应力分析法、移动盆地法[4]，除此之外也可采用隧道工程中的成拱分析法(普式塌落拱理论法)以及相关经验公式[5]。这些方法的本质都是采用物理或力学分析获得坑洞坍塌影响的临界深度hcr与坑洞埋深h，当h/hcr≥K(安全系数)时认为坑洞坍塌影响深度小或不影响，反之则认为影响大，需进行处理。但是由于理论不同，这几种方法计算出的结果差别较大，而且结果一般偏于保守。除此之外段自侠等采用FLAC3D数值模拟，对非规则分布的坑洞进行稳定评价并提出了合理的处理措施[6]；张劳恩采用概率积分法预计模型对采空区间安全廊道进行稳定性分析，并将场地稳定性进行分级[7]；闫明应用 InSAR(合成孔径雷达干涉测量)技术结合物探及钻探等手段，对采空区影响进行综合评价，减少了勘察工作量[8]。

基于以上分析，为了更准确评价人为坑洞的稳定性，以某运营铁路的人为坑洞处理工程为例，对荷载临界深度判别法进行修正，并与其他评价方法计算结果进行对比，分析各种稳定性评价方法的优缺点。

2 坑洞稳定性评价方法

2.1 坑洞坍塌原理分析

坑洞在开挖成型后可能形成土拱，而且力学性能越好的土层越易形成土拱[9-10]。在此过程中，大主应力由垂直旋转为倾斜，越靠近坑洞大主应力越平行坑洞轮廓线(见图1)，此时土拱效应形成[9-11]，坑洞周边土体处于极限平衡状态。在受到列车振动荷载后主应力增大，超出土体抗剪强度或者土遇水饱和，土层力学参数降低，原有的应力状态被打破(见图2)，坑洞塌陷，此时大主应力重新调整，达到极限平衡状态后，土层再次处于稳定状态。整个过程并非一次性完成的，而是呈现“波动性缓沉”[12]。

图1 洞室主应力旋转示意

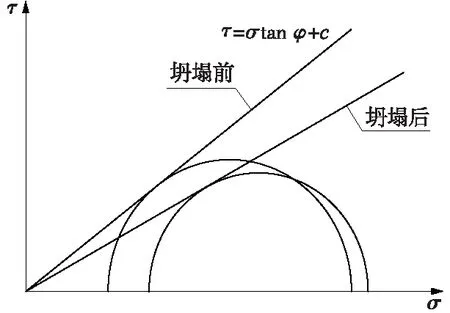
图2 坍塌前后摩尔库仑圆示意

2.2 荷载临界深度判别法及修正

王东等在人工洞穴路基稳定性评价中采用了荷载临界深度判别法，主要原理是将洞顶上覆土层视为刚性体，再由两侧主动土压力提供摩擦力，主动土压力随深度增加而增加，当达到一定深度时摩擦力和土体自重达到平衡(见图3)，这时的深度就是临界深度[13]，计算过程见图3、式(1)。

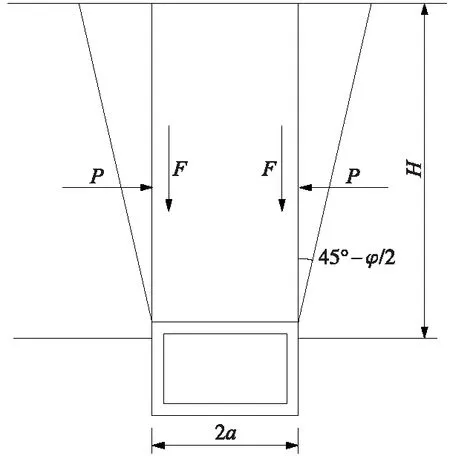
图3 荷载临界深度判别法计算模型

(1)

式中，a为坑洞半宽；γ为土层重度；R为基底压力；φ为综合内摩擦角。

临界深度判别法中，假设破坏面贯通至地面，而且顶部土体所受的侧向土压力为主动土压力，即Ka=tan2(45-φ/2)。此种假设适用于浅埋坑洞，而对于深埋坑洞，由于土拱效应，如果仍采用此种方法，其计算结果偏于保守。

陈若曦等基于主应力轴旋转理论对Terzaghi松动土压力进行修正过程中，通过修改侧向土压力系数Kh来体现土拱效应的形成，其结果如下所示[9]。

对于黏性土，有

(2)

(3)

对于非黏性土，有

(4)

式中，θ=45°+φ/2；Kp=tan2θ。

由式(2)～式(4)可知，黏性土Kh为隐式解，需通过迭代进行试算，在实际工程中需借助计算机才可实现，过程繁琐，而无黏性土Kh计算公式简单，因此将黏性土c、φ简化为综合内摩擦角，采用非黏性土公式进行计算。

除此之外，李国和考虑侧墙稳定的影响，假定破坏面从坑洞墙脚产生，与垂直方向夹角为45°-φ/2，见图4，破坏宽度由a变为a1，同时考虑铁路荷载q，则临界深度可表示为[14]

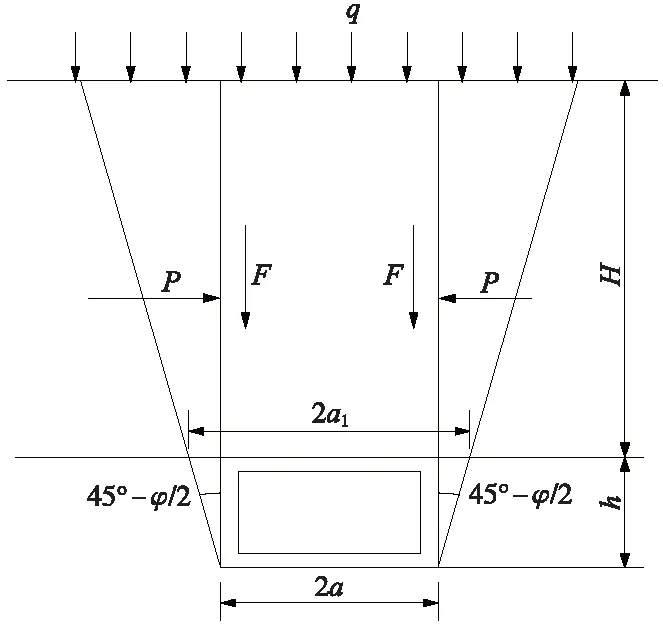
图4 荷载临界深度判别法修正

(5)

式中

同样为了便于计算，采用综合内摩擦角替代c、φ，此时c=0，将式(4)代入式(5)中替代tan2(45-φ/2)，即可求得同时考虑土拱效应和侧墙稳定性影响的临界深度判别公式，即

(6)

式中

θ=45°+φ/2

Kp=tan2θ

a1=a+htan(45°-φ/2)

式中，φ为综合内摩擦角；a为坑洞半宽。

从以上推导过程可以看出，式(6)基于以下假设：①土层为均质土体；②坑洞为深埋，土拱效应已产生；③采用综合内摩擦角计算。

2.3 数值模拟

为了验证计算结果的准确性，基于MIDAS/GTS NX数值模拟软件进行数值模拟。采用2D模型，长20 m，高20 m；坑洞高2 m，宽度为1～2.5 m。本构模型采用摩尔库伦，底部采用固定约束，两侧采用水平侧向约束。土层重度取19 kN/m3，综合内摩擦角取40°，压缩模量取10 MPa，以竖向应力云图的等值线形态为临界深度判别依据，当等值线基本保持水平直线状态时，说明高度大于临界深度，土拱效应充分发挥，土体稳定；反之则说明小于临界深度，此处土体处于不稳状态。计算竖向应力云图见图5～图8。

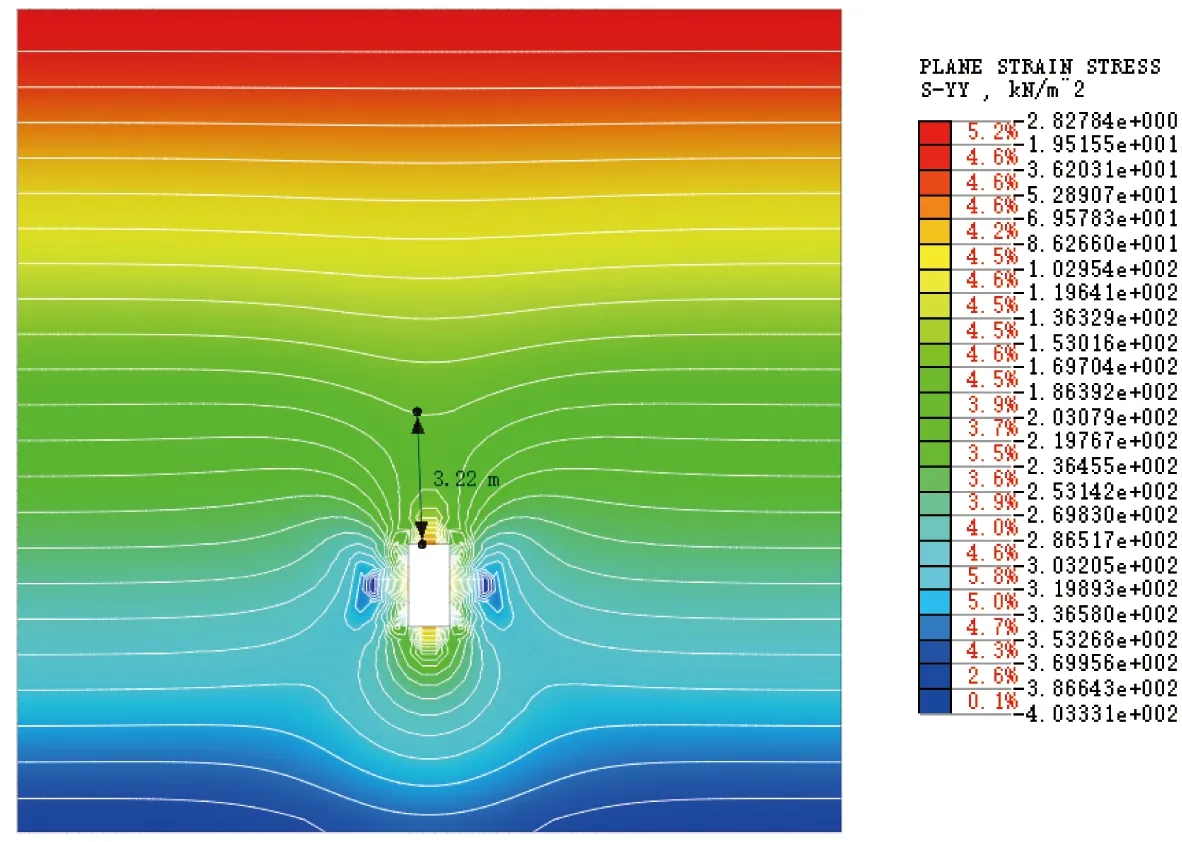
图5 洞宽2a=1 m竖向应力云图

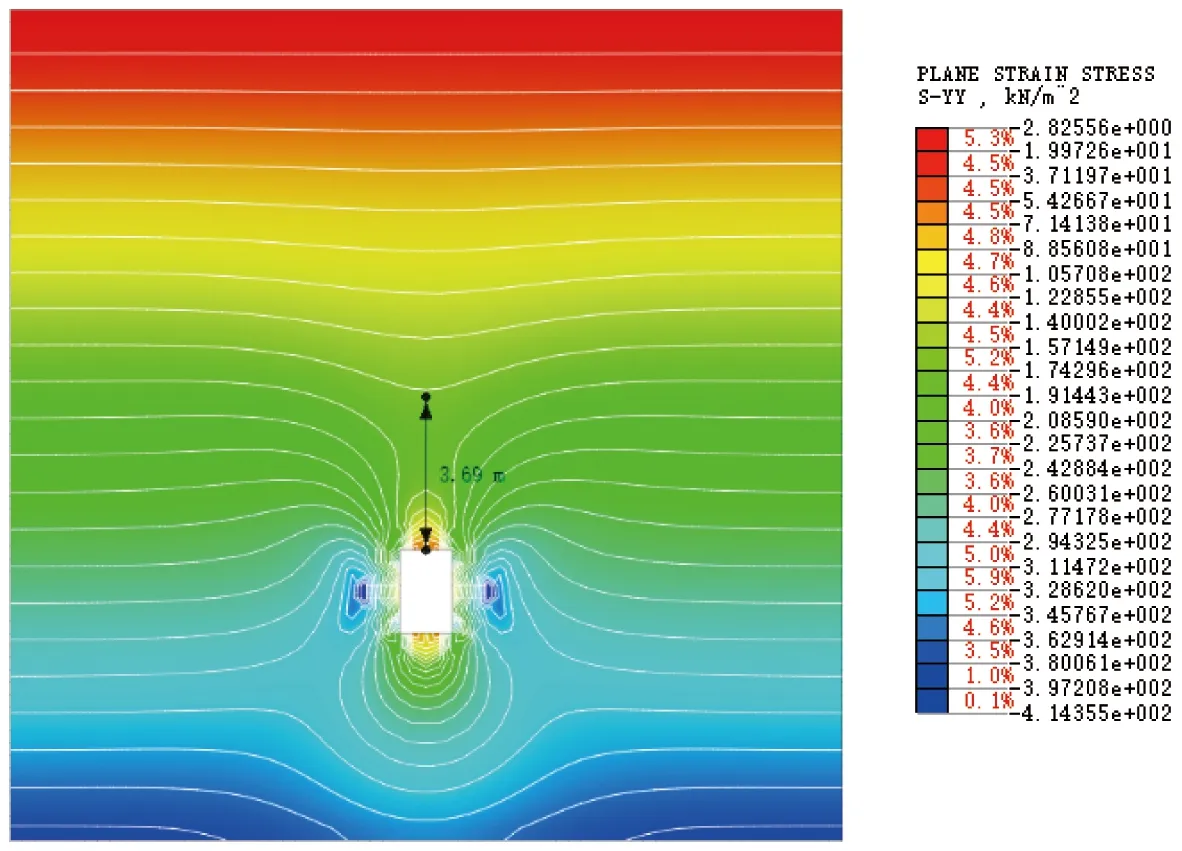
图6 洞宽2a=1.25 m竖向应力云图

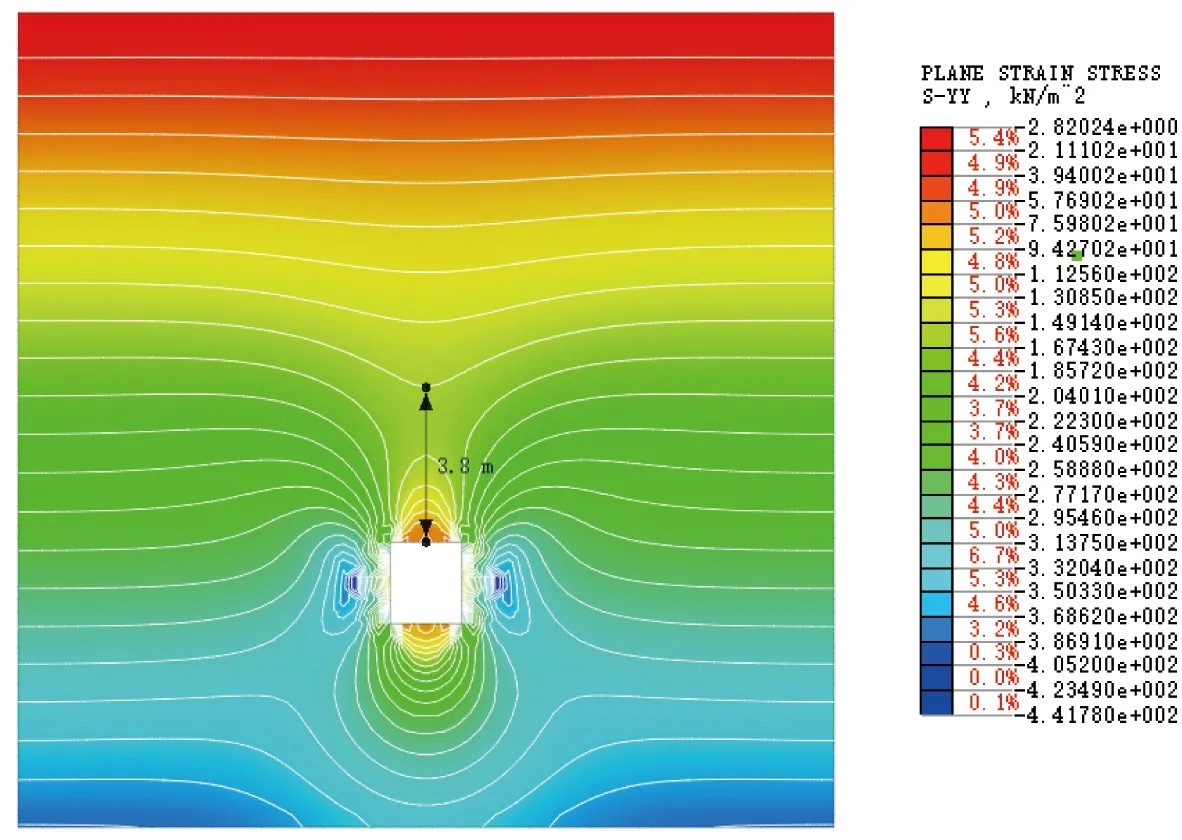
图7 洞宽2a=1.75 m竖向应力云图

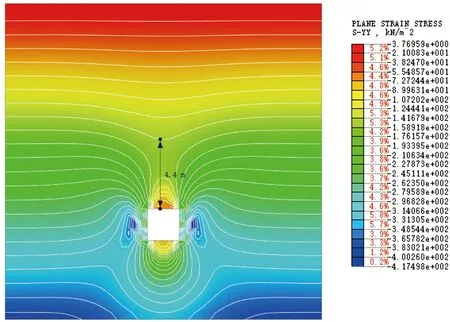
图8 洞宽2a=2 m竖向应力云图

根据图9中修正后荷载临界深度判别法和数值模拟结果，修正后荷载临界深度判别法计算结果比数值模拟计算结果稍高，在坑洞宽度达到2.5 m时，两者计算结果基本一致，但是在实际工程中，人为坑洞宽度一般为1～2 m，因此，修正后荷载临界深度判别法应用在工程中具有一定的安全储备。

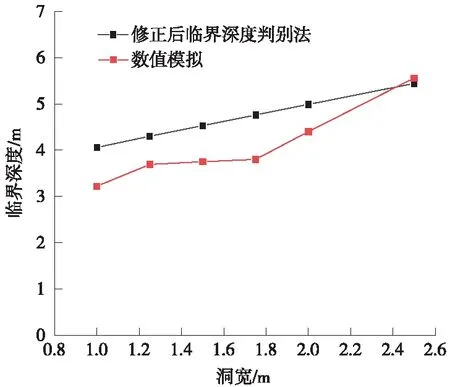
图9 修正后临界深度判别法和数值模拟计算结果对比

3 工程实例

3.1 工程概述

河北境内某运营铁路设计速度为120 km/h，国铁Ⅰ级，线路所在区内山峦起伏，川谷交错，海拔高度在400～980 m之间，沿线经过两类地貌单元，分别为低山丘陵和河谷阶地。沿线地层主要为上更新统冲洪积黏质黄土、粉土。

线路所经区域属中温带半湿润半干旱大陆性季风型高原山地气候。春季风多干旱，夏季湿热多雨，年平均气温为0.9 ℃～6.2 ℃。

场区内存在人为坑洞，主要是防空洞和村民菜窖，因年代久远，洞口多已覆盖，通过现场调查走访、高密度电法以及钻探等勘探方法，发现异常段落22段，现选取位于路基面以下，对路基稳定性影响较大的7段，分别采用顶板坍塌自行填塞法[15]附加应力分析法[16]、普式塌落拱理论法[17]、荷载临界深度判别法和修正后的荷载临界深度判别法进行稳定性评价分析。

3.2 稳定性评价

针对7段勘探异常段落，结合现场调查，推测坑洞走向，在与线路交叉位置各选区1个断面，共计7个断面进行稳定性分析，岩性均为黏质黄土，重度为18 kN/m3，综合内摩擦角40°，不同评价方法对人为坑洞稳定性评价结果结果见表1。

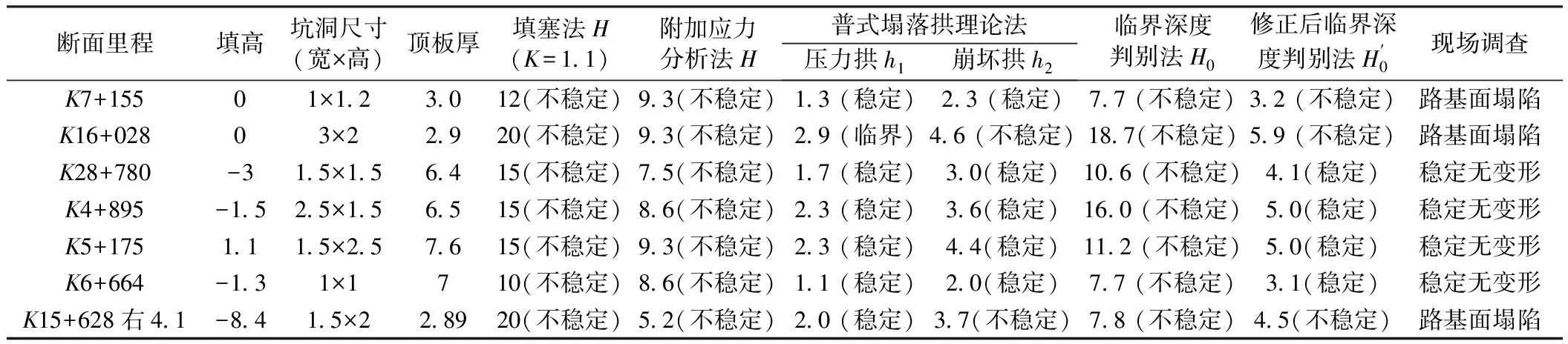
表1 不同评价方法对人为坑洞稳定性评价结果 m

由表1可知，各种方法的得出的临界高度与顶板厚度误差，由大到小依次为填塞法、临界深度判别法、附加应力分析法、普式塌落拱理论法-压力拱法、普式塌落拱理论法-崩坏拱法、修正后的临界深度判别法，修正后的临界深度判别法与结果最符合。

其中填塞法中岩土松散(涨余)系数K受人为经验影响，结果误差较大；附加应力分析法计算结果受路基填挖类型、应力历史影响，局限性较大，其结果也偏于保守；普式塌落拱理论法中压力拱法是在有支护的条件下得出的，其结果不适用于无支护的人为坑洞；崩坏拱法是在无支护条件下洞室自然塌落而形成的，与实际情况较吻合，但其结果较修正后临界深度判别法保守。

4 治理范围

4.1 扩散角计算

在《铁路特殊路基设计规范》[18]中，针对上述工程实例中的情况，采用扩散角法确定加固范围(见图10)。闻继延采用坡脚处向下扩散30°与空洞的交点为处理范围，其原理与扩散角法相似[19]。

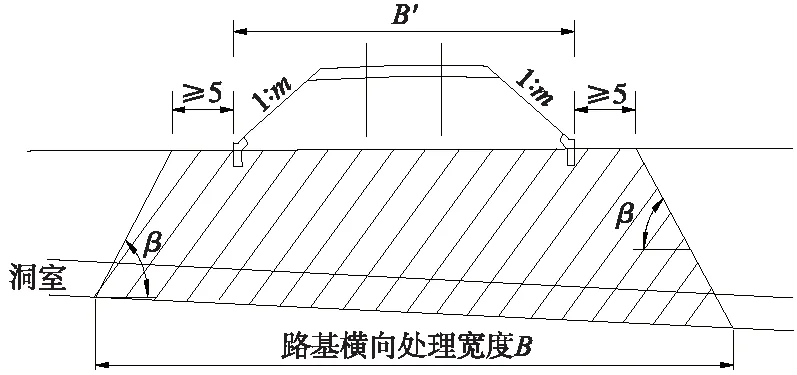
图10 人为坑洞路基基地处理范围

B=B′+10+2Htan(90°-β)

(7)

式中，φp为顶板岩土的综合内摩擦角；B′为路基基底宽度。

4.2 治理范围优化

4.1中的处理范围适用于一般低等级铁路，但是对于等级较高且已经运营的铁路，这样仅依据上述公式得出的结论偏于不安全。佟海宁在扩散角法的基础上加上了围护带的宽度，但是其计算结果针对人为坑洞来说偏大[20-21]。

综上，参考关于围护带的相关规定：路堤应当以两侧路堤坡脚外1 m为界加围护带；路堑应当以两侧堑顶边缘外1 m为界加围护带；围护带宽度根据受护对象的保护等级确定，Ⅰ级铁路≮20 m，Ⅱ级铁路≮15 m。提出了相对经济合适的处理宽度，即

(8)

5 结语

(1)修正后的临界深度判别法综合考虑了土拱效应和侧墙稳定对人为坑洞稳定性的影响，使得其计算结果相较于其他评价方法更加符合实际情况。

(2)修正后的临界深度判别法主要适用于均值土层、深埋坑洞。

(3)黏性土的侧向土压力系数Kh需进行迭代计算，过程繁杂。采用综合内摩擦角按无黏性土考虑可简化计算过程。

(4)坑洞的处理范围除了考虑稳定性外，对于高等级铁路还应考虑变形影响，当坑洞埋深较浅时处理范围应适当扩大。