基于误差状态方程的采煤机滚筒最优控制调高技术的研究

王 宏，许春雨，田慕琴

（1.太原理工大学 电气与动力工程学院，山西 太原 030024；2.太原理工大学 矿用智能电器技术国家地方联合工程实验室，山西 太原 030024）

我国煤矿地质结构复杂[1]，综采工作面设备的自动化技术水平比较低，多数采用人工手动操作采煤机，劳动强度大，存在十分严重的安全隐患，且因工作面粉尘较大，司机无法及时准确地判断截割煤岩状态，难以根据实际情况及时调整滚筒高度达到沿着煤岩界面切割的目的。当滚筒高于煤岩界面时，不仅会增加切割的煤中的含矸量，影响开采的煤炭的质量，也会使采煤机在工作过程中不断截割到坚硬的岩石，大大减少采煤机的工作寿命；当滚筒低于煤岩界面时，会有大量原煤无法开采，造成对煤炭资源的浪费[2-3]。因此，滚筒自动调高技术是采煤机自动化的关键技术。

目前采煤机滚筒调高常用的方法有PID控制法、记忆程控法、滑膜变结构法等。传统PID控制法的控制器结构比较简单[4]，控制参数在系统运行过程中不能调整，而地下采煤环境复杂多变，传统PID技术不能及时调整滚筒高度，有很大的局限性；记忆程控法在煤层变化较大的情况下容易误截割煤岩或有剩煤[5]；滑膜变结构法在到达滑膜面时会上下抖动[6]，破坏系统的稳定性。针对采煤机传统PID调高技术控制滞后和跟踪性能较差的问题，本文将最优控制方法与误差状态方程结合起来[7-10]，控制方法的反馈为全状态反馈，能够提高系统的响应速度，减小跟踪误差。

1 采煤机调高模型

采煤机调高控制系统主要由最优控制器、电液比例阀、液压系统、调高油缸以及位移传感器等[11]组成，其调高过程如图1所示。位移传感器测量调高油缸的位移、速度、加速度并将其反馈给最优控制器，调高最优控制器根据调高油缸当前位移、速度、加速度以及滚筒实际高度和目标高度的差值生成控制信号，在功率放大器中放大之后，作为系统的输入信号，对采煤机滚筒高度进行调整[12-13]。

图1 采煤机调高控制系统结构图

在采煤机电液比例调高控制系统中，电液比例方向阀的响应速度与调高液压缸的响应速度相比，前者明显远大于后者。为了简化整个系统的数学模型，可以把输入电压U与电液比例阀阀芯位移XV之间的关系看作比例关系，即有：

式中：Ka为放大器增益；Ksv为比例阀增益。

通过牛顿第二定律可知，油腔质量及摩擦力等因素忽略不计的前提下，液压缸受力平衡方程为：

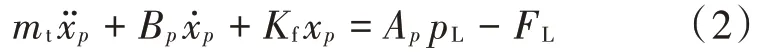
式中：mt为活塞和负载的质量之和；Bp为活塞和负载的黏性阻尼系数；Kf为负载弹性刚度；FL为外负载力；xp为调高油缸活塞位移量；Ap为调高油缸活塞平均有效面积；pL为液压缸进油口和出油口的压力差。

对液压缸而言，在运动过程中一定会产生损耗，如因泄露而产生的损耗、在压缩过程中油液产生的损耗等，将这些因素考虑到流量的计算中，得到如下流量连续方程：

式中：qL为液压缸流量；Ctp为平均泄露系数；Vt为液压缸总压缩体积；βe为体积弹性模量。

调高油缸滑阀的流量公式为：

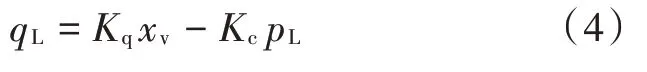
式中：Kq为流量增益系数；Kc为流量-压力系数。

由于在控制系统中活塞与负载的黏性阻尼系数Bp一般都比较小，则，可以忽略，在Kf=0的情况下，将式（1）～式（4）进行拉普拉斯变换后联立求解，得到：

式中：Kce为等效泄露系数；ωh为液压缸固有频率；ξh为液压缸阻尼比，公式如下：

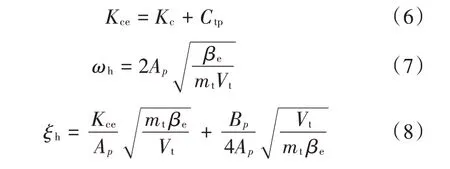
2 最优控制器

2.1 最优控制

最优控制是指当约束条件一定时，寻求一个控制，使系统的某个给定性能指标达到极大值（或极小值）。本文通过构造误差系统，将采煤机滚筒的目标轨迹与实际轨迹的拟合程度用评价函数J来表示，J的值越小，则两条轨迹的拟合程度越好，采煤机的路径跟踪误差越小。当评价函数达到系统性能指标允许的最小值时，即得采煤机跟踪滚筒路径的最优解[14-15]。

2.2 误差系统的构造

将式（5）求出的传递函数转化为离散状态空间方程，公式如下：

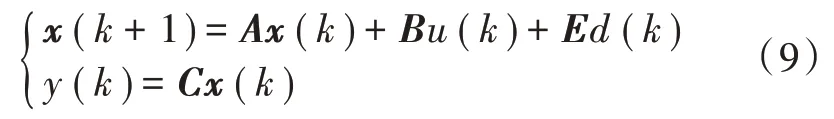
式中：x(k)=[x¨p x˙p xp]T为状态变量，x¨p,x˙p,xp分别表示调高油缸活塞的加速度、速度、位移；d(k)为采煤机在运行时的外负载力；u(k)为输入电压；y(k)为调高油缸活塞位移；A∈R3×3，B∈R3×1，C∈R1×3，E∈R3×1都是常数矩阵。

设离散状态空间方程式（9）可控可观测，目标信号为R(k)，针对离散系统来构造误差系统，步骤如下：

1）求解e(k)的一阶差分值

根据误差信号：

得e(k)的一阶差分值为：

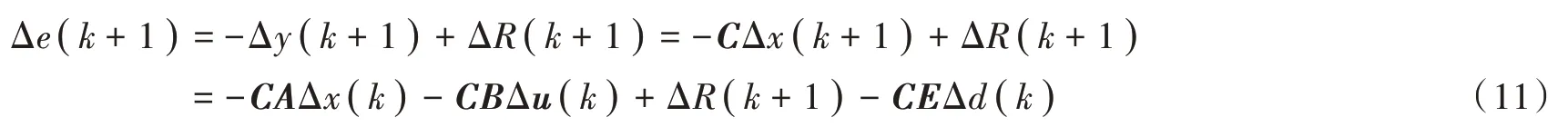
2）求解Δx(k)的一阶差分值

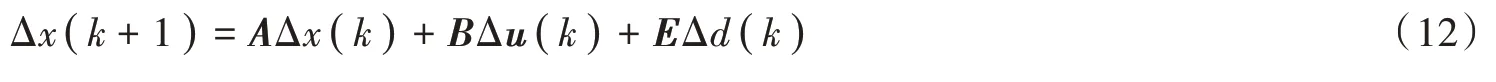
结合式（11）和式（12）得到如下误差系统：

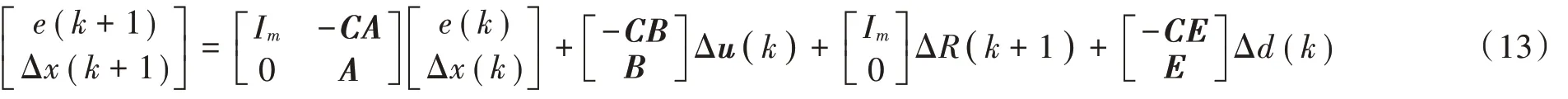
或者表示为：

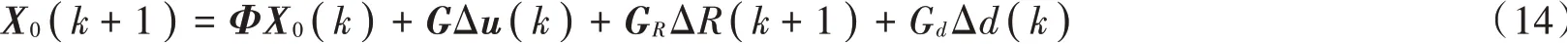
若原离散系统式（9）可控可观测，则误差系统式（13）或式（14）可控可观测。误差系统式（13）或式（14）相应的评价函数为：

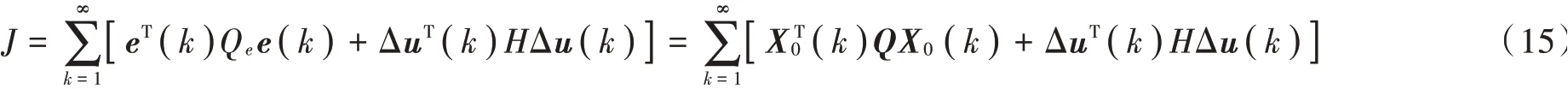
2.3 最优控制器的设计

当ΔR(k+1 )=0，Δd(k)=0时，由式（9）可知此时误差系统的表达式为：

针对误差系统式（16），设计对应的最优控制器，当评价函数式（15）取最小值时，Δu(k)的值即为最优控制输入。当评价函数式（15）取得最小值时，若k→∞，则X0(∞)→0，因此对任意对称矩阵P有：

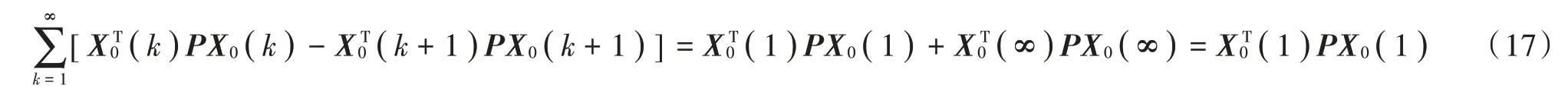
于是评价函数式（15）可以写成：

当式（18）取最小值时，得：

式中：F0=[Fe Fx]；P为黎卡提方程的半正定解。P的公式为：

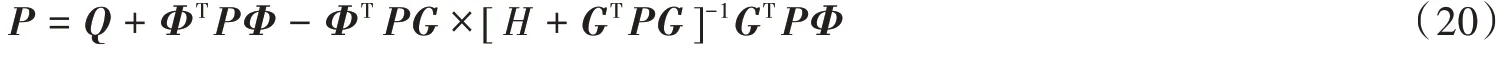
可以看出，最优控制系统主要由状态反馈控制模块组成，系统的结构图如图2所示。

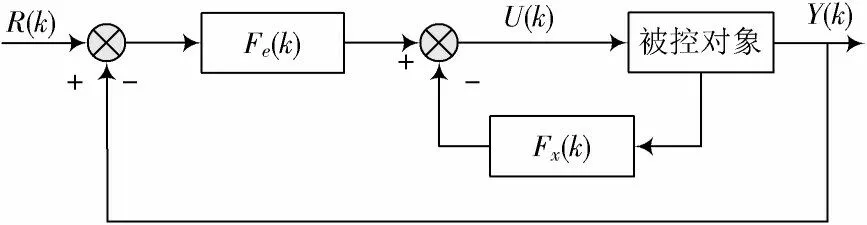
图2 最优控制结构图

3 仿真分析

3.1 系统的相关参数

系统的相关参数如下：

放大器增益Ka为2×106s·A·(m2·V)-1；

比例阀增益Ksv为0.89×10-3m3(s·A)-1；

流量增益系数Kq为0.9 m2·s-1；

调高油缸活塞平均有效面积Ap为22×10-3m2；

等效泄露系数Kce为7.94×10-11m5·(N·s)-1；

液压缸总压缩体积Vt为6.096×10-3m3；

体积弹性模量βe为7×108Pa；

液压缸固有频率ωh为211rad·s-1；

液压缸阻尼比ξh为0.15。

3.2 Simulink仿真

结合最优控制的推导步骤，对上述参数进行整定计算，得到采煤机滚筒调高的最优控制器。利用Matlab/Simulink软件，根据最优控制器设计了系统的仿真模型，并与传统PID仿真模型进行了比较，如图3所示。

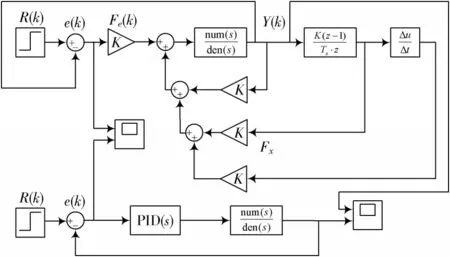
图3 最优控制系统与PID控制系统仿真模型

输入阶跃信号，将仿真时间设定为0.4 s，仿真步长设定为0.001 s，图4为得到的阶跃响应及误差曲线。对图4进行分析可得：在最优控制下，滚筒调高的上升时间为0.021 4 s，超调量为27.1%，稳定时间为0.182 s；而在常规PID控制下，滚筒的上升时间为0.022 1 s，超调量为37.8%，稳定时间为0.235 s。由此可知，在最优控制方法下，滚筒调高的响应速度更快，超调量减少，能更快达到稳定时间。

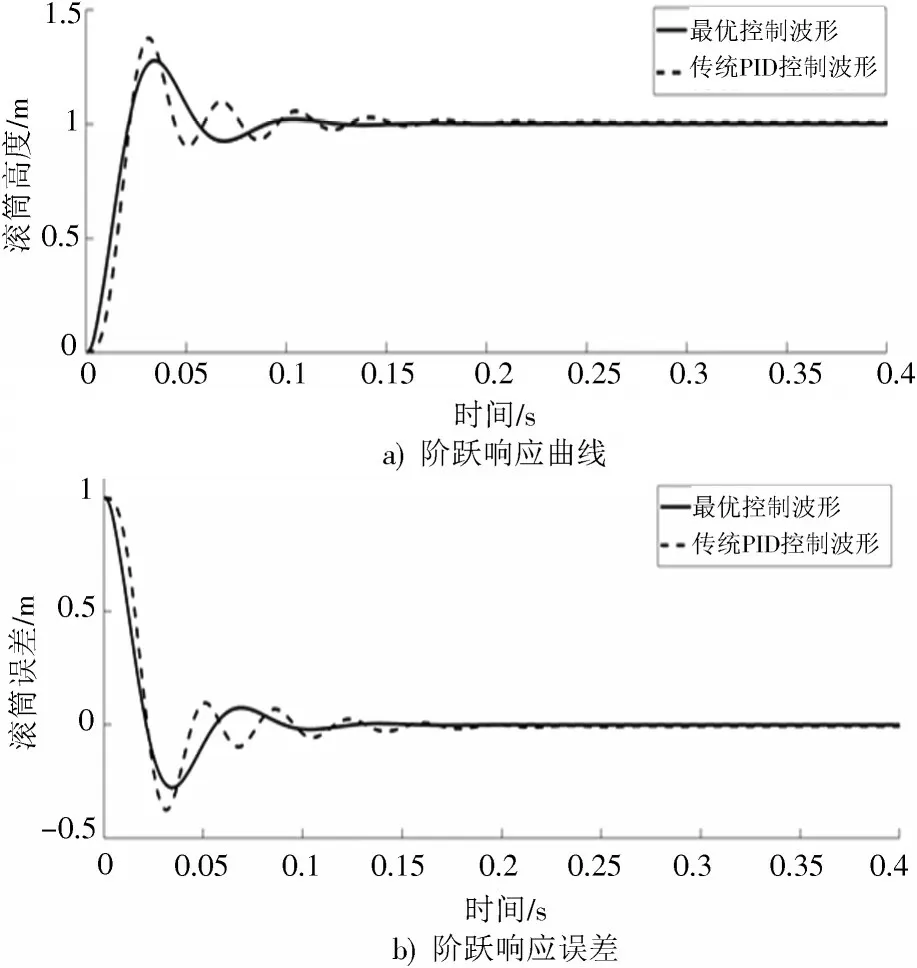
图4 最优控制与传统PID控制阶跃响应曲线及误差

输入正弦信号，设定仿真时间为8 s，仿真步长为0.001 s，图5为得到的路径跟踪误差图。对图5进行分析可得，最优控制方法与传统PID控制方法相比，得到的路径跟踪误差更小，跟踪滞后问题得到明显改善，路径跟踪性能更好。

图5 最优控制与传统PID控制正弦信号跟踪误差

4 结 语

为了改善采煤机传统PID调高控制技术的控制能力和跟踪性能，本文使用基于误差状态方程的最优控制方法对采煤机的调高过程进行控制，推导了采煤机摇臂调高时的数学模型，构造了对应的最优控制器，并在Simulink中搭建了模型进行分析。对仿真波形对比分析的结果表明，最优控制技术能够提高采煤机调高的动态性能和跟踪性能，能够很大程度上提高滚筒自动调高控制技术水平，并且这种控制方法计算过程简单，控制过程很好实现，便于应用到工程实践中。