顾及地球重力场模型的高程转换方法

王式太，肖守圣，殷 敏*，华 磊，姜新伟，程 波

(1. 桂林理工大学 测绘地理信息学院，广西 桂林 541006； 2. 广西空间信息与测绘重点实验室，广西 桂林 541006； 3. 中国地质大学(武汉)公共管理学院，湖北 武汉 430074; 4. 山东省地质测绘院，山东 济南 250013)

0 引言

无人机摄影测量具有分辨率高、成本低和任务周期短等优点[1-2]，通过无人机摄影测量，能够快速得到数字正射影像图、大比例尺地形图和数字高程模型(Digital Elevation Model,DEM) 等数字化成果[3-5]，由于定位定向系统(Position and Orientation System，POS)获得的坐标数据是通过全球导航卫星系统(Global Navigation Satellite System, GNSS)测量得到的，所获得的大地高与正常高之间需要通过高程异常值进行转换[6-8]。通常，求取高程异常的方法有多项式函数拟合、多面函数拟合和神经网络拟合等[9-12]，但几何拟合方法要求拟合区域内要有一定数量且分布合理的水准联测GNSS点，该方法在水准点稀少的测区(尤其是山区)实施困难且山区高程异常变化较大时精度会受到较大影响[13-14]。任超等[15]使用不同组合方法对高程异常拟合进行讨论，发现WLSSVM组合和非负变权组合的拟合效果较好，转换精度较高。刘斌等[16]提出了一种基于EGM2008地球重力场模型和地形变化的影响，并结合二次曲面函数来进行高程拟合，该方法能提高GPS高程拟合精度。马雷等[17]使用EGM2008，EIGEN6C4，GOCO05S三种地球重力场模型与克里金插值和一些函数拟合方法来进行精度分析，证明了地球重力场模型与数学函数相结合的“移去—恢复”法的优势。然而，对于不同几何模型与不同地球重力场模型的结合效果未进一步研究，也未将其应用到无人机摄影测量领域。本文采用平面函数、二次曲面函数和多面函数3种几何模型以及EGM2008，EIGEN6C2，EIGEN6C4三种重力场模型。利用已知数据，通过设计不同组合方案进行分析和对比，得到了精度较高的组合模型，并将该模型应用于无人机摄影测量，验证模型得到的高程异常精度。结果表明，EIGEN6C4地球重力场模型与二次曲面函数相结合的拟合模型能较好地提高无人机摄影测量成果的高程转换精度，给工程应用提供了一定的参考价值。

1 重力场模型与几何模型结合的高程异常拟合算法

1.1 高程异常与重力场模型的关系

通过Bruns公式来计算地球重力场与高程异常二者之间的关系：

Sn,msin(mλ))Pn,m(sinθ) ，

(1)

式中，ζG为该点用地球重力场模型计算得到的高程异常值；(ρ,θ,λ)分别为地心向径、地心纬度和地心经度；GM为引力常数和地球质量的乘积；γ为待定点的正常重力值；a为参考椭球的长半轴；Cn,m,Sn,m为完全规格化得到的位系数；Pn,m(sinθ)为完全规格化的Laggardness函数；N为模型的最高展开阶数。

1.2 重力场模型

随着测量技术的不断发展，不同地球重力场模型的分辨率和精度持续提高。本文选用了广泛使用的3种典型地球重力场模型进行实验分析。

① EGM2008地球重力场模型：由美国国家地理空间情报局2008年研制的全球超高阶重力场模型，采用WGS-84坐标系，阶次达到2 190。相比于以前的低阶重力场模型，EGM2008重力场模型精度有着大幅度提高[16]。在一些精度要求不高的场合，可以使用它来获得相应的数据。

② EIGEN地球重力场模型：EIGEN6C2重力场模型是德国地学中心2012年发布的1 949阶的重力场模型；EIGEN6C4重力场模型是德国地学中心在2014年发布的2 190阶的超高阶重力场模型[13]。该模型的中长波精度有较大提升，是目前精度最高的重力场模型。

1.3 “移去—恢复”法原理

将高程异常分为3部分：长波项、中波项和短波项。短波项是地形起伏引起的，需要结合测区的数字高程模型来进行地形改正。但在实际应用过程中数字高程模型通常难以获得，因此一般不进行地形改正。可以将高程异常分为2部分：

ζ=ζG+Δζ，

(2)

式中，ζG为用地球重力场模型计算得到的高程异常值；Δζ为实际测量得到的高程异常与地球重力场模型计算得到的高程异常残差值。

“移去—恢复”法的具体实现过程与技术路线如下：

第1步“移去”：测区中选择n个GNSS点，其中m个GNSS点含有大地高H与正常高Hγ，可以求解得到m个水准点的高程异常值ζ=H-Hγ，通过相应的地球重力场模型计算得到m个GNSS点的近似高程异常值ζG，m个GNSS点的高程异常残差项Δζ(Δζ=ζ-ζG)；

第2步“拟合”：对第1步求得m个GNSS点的Δζ，利用常规的几何函数对此残差进行拟合，求解得到相应模型的拟合系数，将剩余点的Δζ利用上述的几何函数进行拟合求解；

第3步“恢复”：将第1步利用地球重力场模型解算得到待定点的ζG与第2步中拟合求得待定点的Δζ相加，求得待求点的最终高程异常值ζ=ζG+Δζ，得到各待求点的正常髙。

2 实例分析

2.1 高程转换实例方案

以文献[18]中的丘陵地区测量数据作为本文的实验数据。该测区西北方向地势较高，东南方向地势较低。测区内部以海拔650～850 m的丘陵为主，还有一些浅丘和平坝，其中海拔850 m以上的高山也占了很大的比例。实验选取了测区中17个GNSS点作为实验点，其中有3个国家一等水准点，其余点以一等水准点为基准点，按照国家四等水准测量规范进行水准测量，得到质量可靠的正常高数据。名山测区控制点分布示意如图1所示。实验结果采用中误差、内符合精度和外符合精度进行转换精度评定。

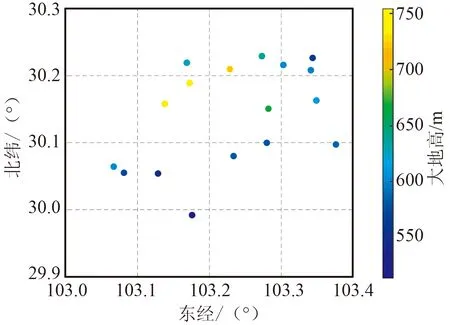
图1 名山测区控制点分布示意Fig.1 Distribution of control points in Mingshan

2.2 方案1

选取测区内均匀分布的6个控制点作为已知点进行实验，其余11个点作为检核点。采用不同的拟合函数与不同的重力场模型进行拟合，包括几何函数拟合、平面函数拟合(Planar)、二次曲面拟合(Quadratic)和多面函数拟合(Polyhedral)；顾及EGM2008地球重力场模型进行高程转换；顾及EIGEN6C2地球重力场模型进行高程转换；顾及EIGEN6C4地球重力场模型进行高程转换。精度分析汇总如表1所示。点位分布如图2所示。残差如图3～图6所示。

表1 方案1精度分析汇总Tab.1 Summary of precision analysis of scheme 1 单位：m

图2 方案1点位分布Fig.2 Point distribution of scheme 1

图3 几何函数拟合残差Fig.3 Residual graph of geometric function fitting

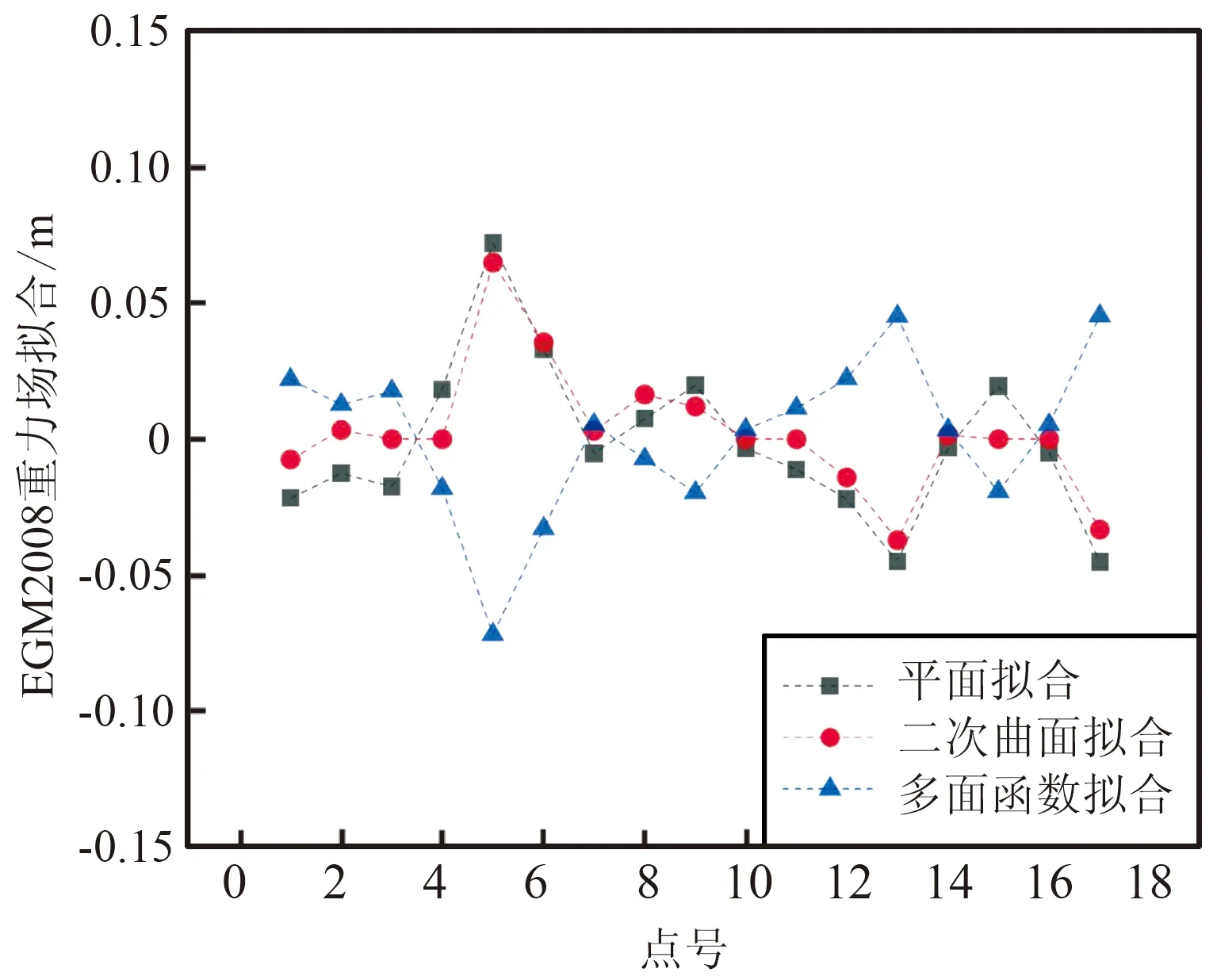
图4 EGM2008地球重力场的残差Fig.4 Residual graph of EGM2008 earth gravity field

图5 EIGEN6C2地球重力场的残差Fig.5 Residual graph of EIGEN6C2 earth gravity field

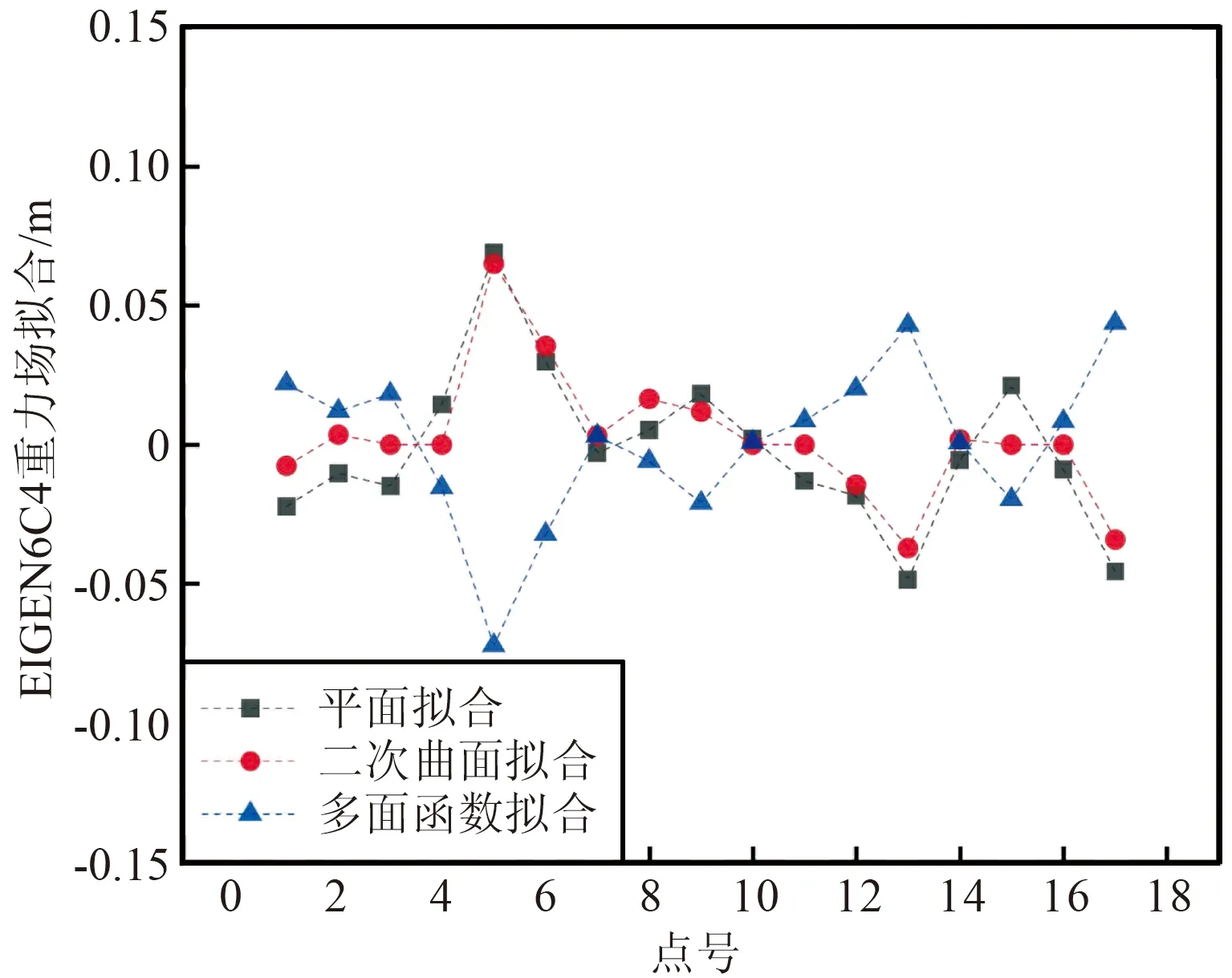
图6 EIGEN6C4地球重力场的残差Fig.6 Residual graph of EIGEN6C4 earth gravity field

由表1可以看出，基于二次曲面函数拟合法的精度较其余2种拟合方案高，中误差为0.025 m，外符合精度为0.032 m，平均值为0.005 m。通过比较基于不同地球重力场模型的“移去—恢复”法的高程转换精度可以看出，基于3种不同地球重力场模型的高程转换结果中残差的最大值、最小值、中误差、平均值以及外符合精度都比单一的几何函数拟合得到的结果小。通过残差图同样可以看出，得到的精度较高。在3种不同的重力场模型之间进行比较发现，使用EIGEN6C2重力场模型的精度较差，使用EGM2008重力场模型的精度与EIGEN6C4重力场模型的拟合精度相当，但基于EIGEN6C4地球重力场模型进行高程转换结果的拟合残差值中平均误差较小，得到的精度更加可靠，更适合用作高程异常拟合计算。顾及EIGEN6C4重力场的二次曲面函数拟合的中误差为0.023 m，外符合精度0.030 m，平均值0.003 m，约为单一的二次曲面函数拟合的平均值的1/2，得到的结果更加可靠。

2.3 方案2

选取测区内均匀分布的9个已知高程异常的点进行拟合函数系数计算，其余8个点作为检核点。采用的拟合函数和重力场模型同方案1。点位分布如图7所示。将上述4个方法计算得到的高程异常残差值进行精度分析，不同方法的二次曲面拟合残差如图8所示，精度分析如表2所示。

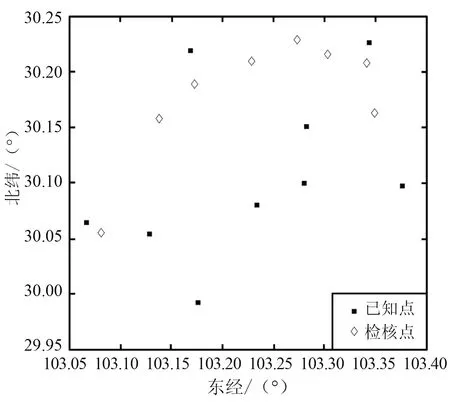
图7 方案2点位分布Fig.7 Point distribution of scheme 2

图8 几种不同方法的二次曲面拟合残差Fig.8 Residual graph of quadric surface fitting with several different methods

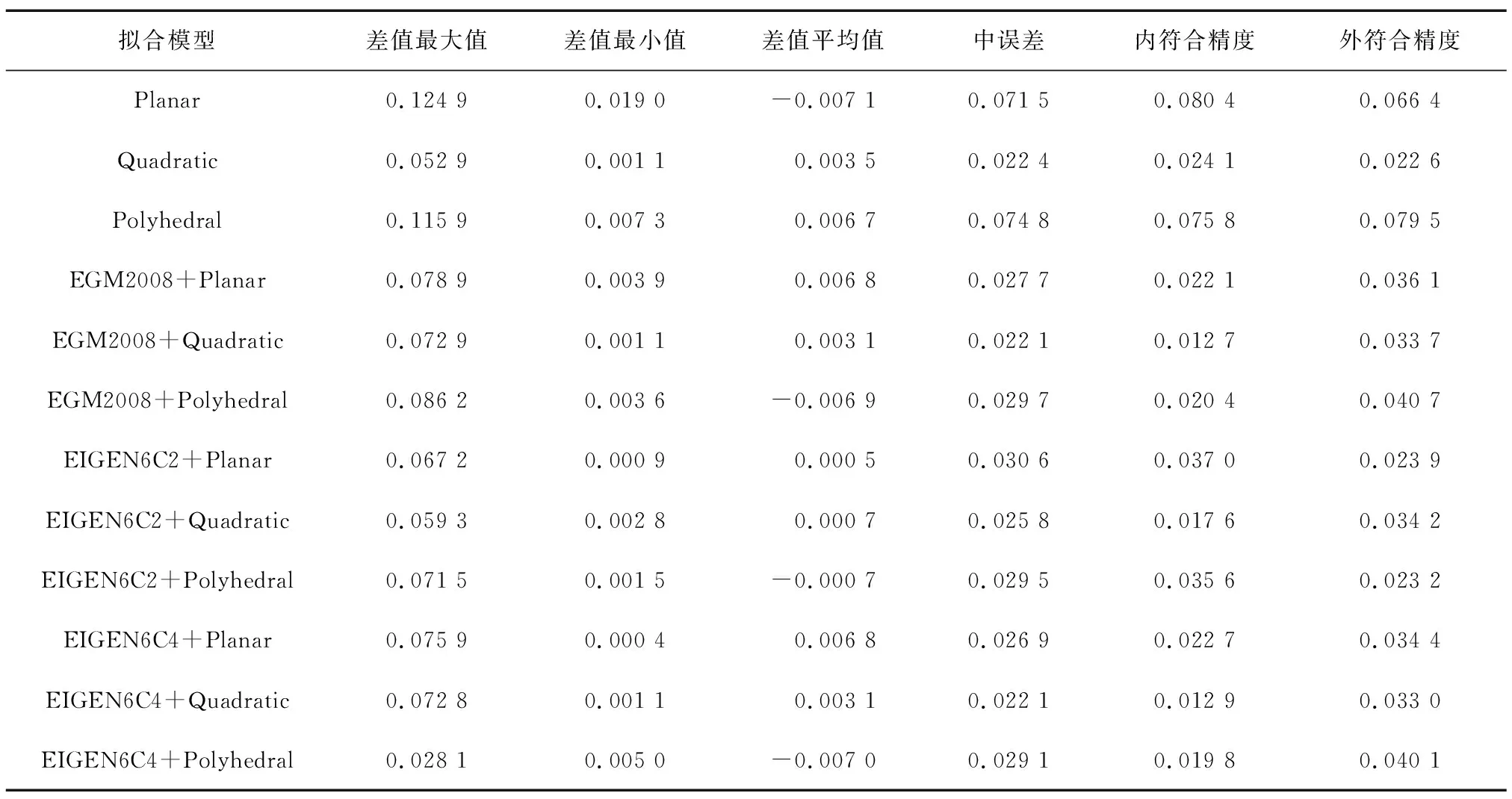
表2 方案2精度分析Tab.2 Summary of precision analysis of scheme 2 单位：m

当选取测区内数量较多、分布均匀的已知点时，使用几何函数拟合中的二次曲面拟合的中误差能够达到0.022 4 m，能较好地进行高程异常拟合。顾及不同地球重力场模型和二次曲面拟合相结合时的精度对比其他2种方法的拟合精度仍有较大提升，其他2种函数拟合的精度可以达到与二次曲面函数相当的水平，中误差均缩小到了3 cm之内，相对几何函数中的7 cm误差，是一个较大的提升。由图8可以看出，顾及地球重力场模型的二次曲面拟合比单一的二次曲面拟合波动和残差平均值都较小，这也说明了考虑地球重力场模型的高程转换精度有一定的提升。

综上所述，通过以上2个方案的结果可以看出，在地形起伏较大的山区进行高程异常拟合时，选用二次曲面函数和EIGEN6C4地球重力场模型相结合的拟合方法来进行高程转换计算是最佳的选择。

3 高程转换在无人机摄影测量中应用

实验使用大疆御Mavic Pro无人机进行影像数据采集，测区位于广西壮族自治区钦州市石瓯山水库；覆盖面积约为1.4 km2，测区以小山丘为主，最大高差约为100 m，无人机可视性良好。在内业数据处理中，利用Pix4Dmapper软件进行影像处理，通过ArcGIS进行点云数据的处理，得到数字高程模型。选取的点位位置分布如图9所示。

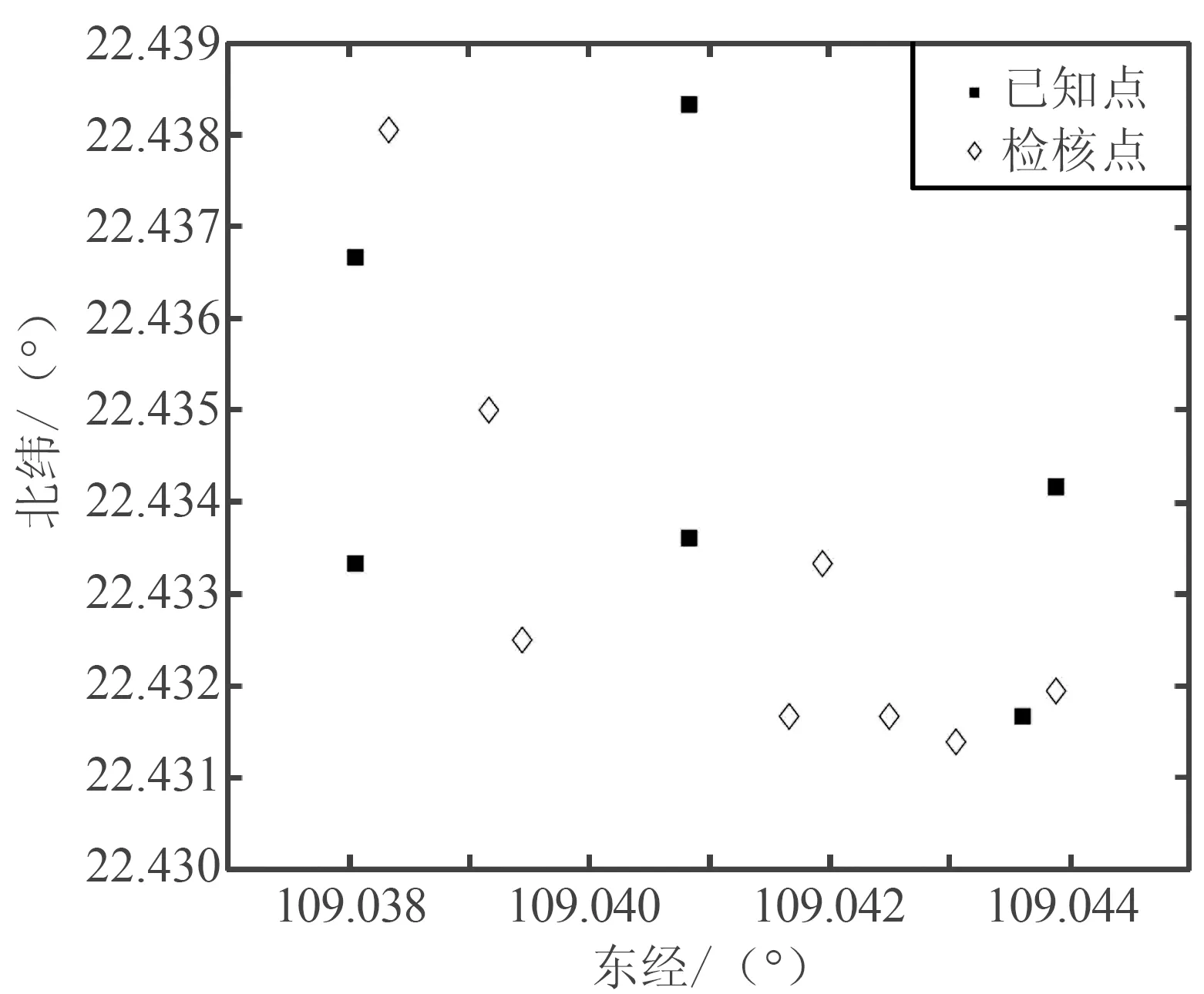
图9 选取的点位位置分布Fig.9 Distribution of selected points

为分析高程转换精度，通过正射影像选取具有代表性的特征点进行处理。本文选用测区中6个像控点作为已知点，选择8个特征点进行精度评定。分别采用3种不同的方法进行高程异常计算和精度评定：① 通过Pix4Dmapper软件与GNSS测得的像控点坐标数据经软件直接处理，得到特征点的正常高；② 利用二次曲面函数根据像控点的坐标数据来求解特征点的高程异常并获得正常高；③ 利用上述顾及EIGEN6C4地球重力场模型与二次曲面函数拟合的方法，求解特征点的高程异常并获得正常高。点位与不同方案得到的高程异常如10所示。

由图10可以看出，直接使用Pix4Dmapper软件进行影像处理，得到的特征点正常高与真实值偏差较大、精度较低且波动较大。使用函数拟合的方法进行特征点高程转换时，8个特征点的高程转换精度有明显提升，误差较小，误差波动较平缓。

图10 不同方案得到的高程异常Fig.10 Height anomalies obtained by different schemes

无人机特征点高程转换分析如表3所示。

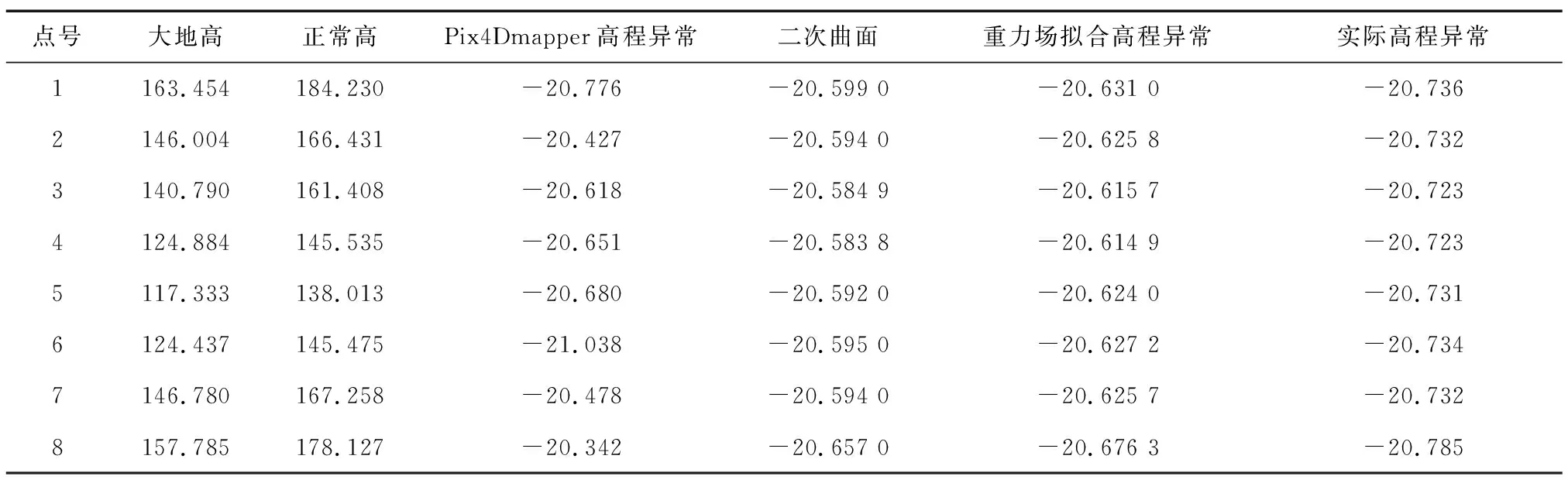
表3 无人机特征点高程转换分析Tab.3 Height conversion analysis of UAV feature points 单位：m

由表3可以看出，直接使用软件处理得到的高程异常中误差为22 cm，使用二次曲面函数进行高程转换的中误差为3.73 cm，顾及EIGEN6C4地球重力场模型时，中误差进一步缩小为1.154 cm。由此可知，顾及EIGEN6C4重力场模型进行拟合的结果更贴近真实值，能够提高高程异常内插的精度。因此，在地形起伏较大的测区进行无人机摄影测量和内业数据处理时，通过应用上述相关的高程转换方法，能够提高无人机摄影测量计算得到正常高的精度。

4 结束语

综合上述实验分析，可以得到以下结论：

① 进行高程异常拟合时，应该结合实际测区情况采用多种方案进行比较分析，得到最佳的拟合模型。综合来说，当测区的已知点分布较均匀而且已知点个数较多时，通常选用二次曲面函数拟合。

② 在顾及地球重力场模型的转换方法中，相比于几何函数拟合法，精度和可靠性均有一定提升，充分利用GNSS的高程信息和地球重力场模型提供的中长波部分，可以获得较大的精度提升，较大地减少水准测量的外业工作，提高作业效率。

③ 在无人机摄影测量数据处理中，相对于软件直接处理输出得到的正常高，使用高程转换模型得到的正常高有明显的精度提升。说明了顾及地球重力场模型的高程异常内插在无人机摄影测量数据处理中的可行性，对提高无人机摄影测量正常高的精度提供了一定的思路。

本文采用平面函数、二次曲面函数和多面函数3种几何模型和3种重力场模型进行高程异常的计算，未来可在此基础上结合机器学习等算法进一步实验。