融合最近邻矩阵与局部密度的自适应K-means聚类算法

艾力米努尔·库尔班，谢娟英，姚若侠

陕西师范大学 计算机科学学院，西安710119

聚类（cluster）是数据挖掘进行数据分析时常用的方法之一，与对已知样本属性的数据构造划分的监督学习（supervised learning）不同的是，聚类分析属于无监督学习（unsupervised learning），即在数据数量、数据属性和数据类别个数等信息未知的情况下进行自主学习，最后构造划分的过程[1]。传统Kmeans 算法[2]适用范围较广，在处理大数据时具有较高的相对伸缩性，其典型的特点是，当数据样本集接近正态分布，且不同聚类的界限划分较为明显时，传统K-means 聚类效果能够达到最优，因此被广泛地应用于各个领域中[3-5]。但是使用传统K-means 聚类算法也会受到一定的限制。由于传统K-means 算法随机选取初始聚类中心点，易收敛于局部最优解，在聚类过程中也容易受到离群孤立点的影响，同时传统K-means 算法需要预先人工输入聚类数目K值，导致聚类效果不稳定且算法自适应能力较弱。近年来，大量学者主要从以下三方面针对传统K-means 聚类算法的缺陷和不足提出了一系列改进：

其一，针对离群孤立点在一定程度上使聚类结果出现偏差的问题，文献[6-7]将基于距离的离群点检测（local outlier factor，LOF）引入传统K-means 聚类算法，根据LOF 算法中计算异常因子的方法计算数据对象的局部异常程度。在此基础上，文献[8]通过计算数据对象的K 近邻，预先对数据集构建平分树,然后通过剪枝检测数据集中的全局离群点。这虽然在一定程度上提高了聚类结果的准确性和时效性，但在聚类过程中仍然需要人工输入聚类数目K值，对数据集分布的研究不够深入和透彻时，聚类效果依旧不稳定。

其二，针对传统K-means 算法对初始聚类中心敏感的缺点，文献[9]用余弦相似度替换文本聚类的距离度量标准，文献[10]选取数据样本集中方差最小且处于不同区域的数据对象作为初始聚类中心，文献[11]采用Pearson 相关系数统计数据对象间的相关性。虽然这几种方法都提出选取初始聚类中心的有效方案，但是在聚类过程中不仅需要人工预先指定聚类中心数目K值，还需进行大量计算，增加了算法的时间开销。

其三，针对传统K-means 算法需要人工输入聚类数目K值的问题，文献[12]首次将密度峰值原则应用到聚类算法中，提出快速搜索密度峰值聚类算法。该聚类算法以数据样本集中的密度峰值点作为初始聚类中心，从而确定聚类数目K值。尽管如此，密度峰值聚类算法还是需要人为主观选择参数。文献[13]通过构造样本距离相对于样本密度的决策图，自适应确定聚类个数K值。文献[14]预先对数据集用密度权重Canopy 算法进行聚类,目的在于为传统Kmeans 算法提供初始聚类中心和最优聚类数目K值，但Canopy 算法初始阈值人为指定的问题仍然存在。文献[15]定义了数据对象K 近邻内的局部密度，提出了模糊加权的K 近邻密度峰值聚类算法（fuzzy weighted K-nearest neighbors density peak clustering，FKNNDPC），该算法先后使用两种分配策略对聚类中心点、非中心点和离群点构造划分。这些算法在聚类过程中有效避免了传统K-means 算法易陷入局部最优解的问题，倘若在聚类过程中没有把握好阈值，则会直接造成获得的初始聚类中心点与实际中心发生较大偏差，极大程度降低聚类精确度。

这些改进K-means 的聚类算法在提高了传统Kmeans 算法聚类效果的同时也优化了聚类算法的性能，但依然存在对噪声数据敏感、需要主观确定一些参数和阈值的不足。针对以上现有问题，通过分析最邻近吸收原则与密度峰值原则的优缺点，改进算法采用最近邻矩阵与局部密度优化的双重策略，不需要人为干预与任何参数的选择，进而实现初始聚类中心及聚类数目的动态确定。在聚类过程中，不仅考虑到离群孤立点对聚类效果的影响，同时也增强了聚类效果的稳定性与客观性。

1 基本原则介绍

1.1 最邻近吸收原则基本原理

最邻近吸收原则（nearest-neighbor absorbed first principle）[16]：在多维空间中，任意一点与它最邻近的样本点属于同一类簇的可能性较大。在聚类算法中的典型应用为K 邻近吸收原则与ε邻近吸收原则。其中，K 邻近吸收原则的基本原理是目标对象吸收与其属性最相似或者距离最邻近的K个邻居，ε邻近吸收原则的基本原理是目标对象吸收以自身为中心，在ε为半径的领域内所包含的数据对象。当数据样本集呈正态分布时，利用最邻近吸收原则构造数据划分的结果最为理想。

若将K 邻近吸收原则直接应用到聚类算法，参数K和ε值的大小直接影响聚类类簇的数目，且该原则只会考虑到样本之间的相对位置，而无法考虑到样本集整体的分布情况，会导致聚类算法不具有较高的鲁棒性。

无论是K 邻近吸收原则还是ε邻近吸收原则都具有以下缺点：

（1）需要根据经验预先确定K值或ε值，参数的取值直接影响聚类结果的好坏。

（2）不能有效测量数据对象之间的相关性或差异性，无法识别流形数据集。

1.2 密度峰值原则基本原理

密度峰值原则（density peak principle）[12]：在多维空间中，聚类中心点的局部密度大于在其余数据样本点的局部密度，且在聚类算法中两个聚类中心点的相互距离相对较远。此时，聚类中心点在数据样本集中具有较优的分布性。密度峰值原则利用截断距离dc计算当前数据样本集的局部密度与数据对象之间相对距离，当数据样本集密度分布较为平均时，聚类的效果最为理想。

与最邻近吸收原则相反，密度峰值原则考虑的是全局分布特点，而忽略了数据对象局部领域内的分布情况。该原则能够识别各种形状的数据样本集，但是针对密度变化较大或类簇间差异较大的数据集，往往会降低容错性。若将密度峰值原则直接应用到聚类算法中会导致算法具有较差的计算精度。同时，密度峰值原则具有以下缺点：

（1）在实际聚类应用中离群点会直接导致数据样本集的平均密度变大，从而影响聚类效果。

（2）过度依赖参数截断距离dc的设置，参数的取值直接影响聚类结果的好坏，如果缺乏经验，也会降低聚类效率。

2 基本概念

针对上述最邻近吸收原则以及密度峰值原则存在的明显缺点，改进算法融合距离矩阵与局部密度的思想，动态确定聚类中心点数目以及位置，完成剩余数据对象的初分配。为了方便后续算法的说明与描述，给出以下定义。

对于给定的含有n个样本的数据集Dn={X1,X2,…,Xn}，其中样本数据集Dn含有p个属性{A1,A2,…,Ap}，即n为数据样本集所含样本总数，p为样本数据集Dn的维度。

对于数据集Dn中的任意两个样本Xi={Xi1,Xi2,…,Xip}和Xj={Xj1,Xj2,…,Xjp}（1≤i≤n，1≤j≤n，i≠j），其中Xir和Xjr（1≤r≤n）分别对应样本Di和样本Dj的第r个属性的具体数值。记K个聚类中心分别为C={C1,C2,…,Ck}。

定义1（欧氏距离[14]）任意两个数据对象Xi和Xj之间的欧氏距离：

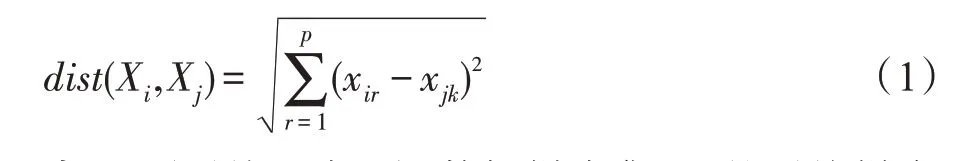
定义2（平均距离[17]）数据样本集Dn的平均样本距离：

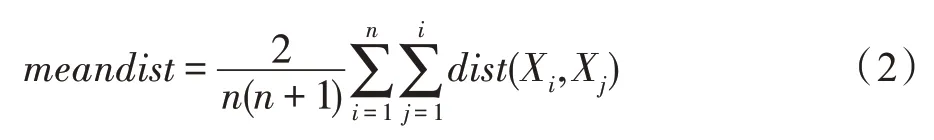
定义3（距离差异）任意两个数据对象Xi和Xj之间的距离差异值：

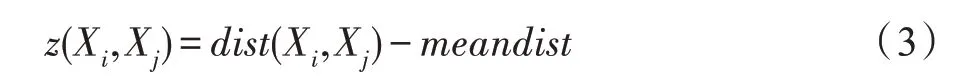
z(Xi,Xj)表示数据样本集中第i个数据对象Xi与第j个数据对象Xj之间的距离差异值。z(Xi,Xj)的数值越小，则代表数据对象Xj成为初始聚类中心的可能性越大，该值的大小直接反映了第j个数据对象Xj是否适合作为第i个数据对象Xi的聚类中心。

定义4（近邻矩阵）数据对象之间的两两距离差异值构成近邻矩阵，它是如下形式的对称矩阵：

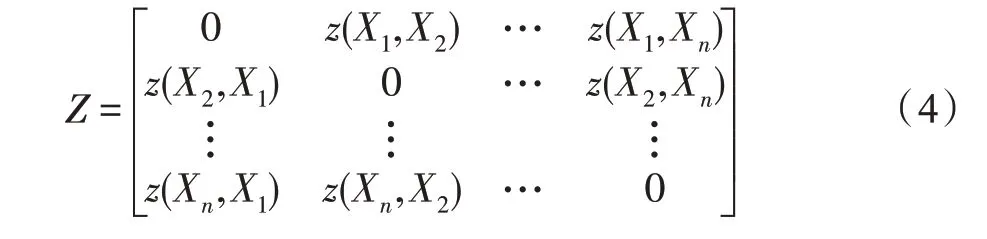
3 改进算法整体介绍

输入：目标数据集Dn。

输出：二维数据集可视化动态聚类视图。多维数据集K个聚类集以及相应的评价指标。

本章从数据预处理、局部密度峰点、数据对象分配策略以及聚类中心点的更新四方面对改进算法进行阐述。

3.1 数据样本集预处理

3.1.1 数据归一化处理

数据样本集由多个维度或多个属性构成，不同的属性变量具有不同的表示单位和不同的密度分布，十分不利于数据解释。数据归一化不仅方便后续的数据处理，也能保证算法迭代时的收敛速度，在涉及到距离计算的聚类算法中有显著效果。

改进算法采用Min-Max 标准化方法对多维数据进行归一化处理，即将数据样本集中属性Ai的原始数值x通过Min-Max 标准化公式映射到区间[0,1]中的值x′，设minAi和maxAi分别为属性Ai的最小值与最大值，则Min-Max 标准化公式为[17]：

3.1.2 离群孤立点检测

对于离群孤立点的判定，改进算法考虑全局离群孤立点，是因为如果仅仅考虑基于密度的局部离群点检测，时间复杂度高且不适用于大规模数据集和高位数据集。在样本空间中，全局离群孤立点相比其他数据对象，具有不同的行为或不一致的特征，即它们是数据集中不与其他数据对象强相关的对象。离群点检测在动态算法中的应用为：在数据归一化之后，若数据对象邻域内的局部密度值小于样本数据集的平均密度值，则标识该数据样本点为数据样本集的离群孤立点。

在数据预处理中对离群孤立点进行筛选的必要性在于，避免离群孤立点对聚类中心点和聚类结果的负面影响，从而提高聚类算法效率。

3.2 确定初始聚类中心

文献[18]定理1 已证实，基于密度峰值原则的聚类算法所得到的聚类中心，其局部密度往往大于其邻居的局部密度。在排除离群孤立点之后，稀疏区域的低密度数据对象成为初始聚类中心的可能性较小。因此，聚类中心往往出现在密度较大的区域。

定义5（局部密度）数据对象Xj的局部密度：

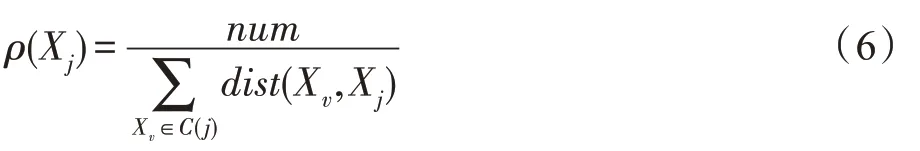
其中，num是在考察目标点最近邻的近邻的过程中，满足近邻条件的样本点数量，即目标点最近邻的最近邻也是目标点的近邻，C(j)是对于目标点Xj满足近邻条件的集合。数据对象的局部密度不仅直接反映了目标点近邻的数量，也反映了目标点近邻的分布情况。

定义6（平均密度）数据样本集Dn的整体密度均值：

分析式（7）可知，数据样本集Dn的整体密度均值与数据的分布密不可分，体现了数据样本集Dn在空间中的紧密程度。

从直观上解释，为了确保初始聚类中心具有良好的连通性，改进算法利用目标点的近邻数目计算数据对象的局部密度，对数据对象采取距离差异值和局部密度相结合的方式选取初始聚类中心，根据式（6）标记局部密度峰点作为一个初始聚类中心，从而有效解决了密度峰值聚类算法在计算数据对象密度时，对截断距离等参数敏感的问题。

3.3 分配数据对象

3.3.1 左、右最近邻

定义7（左、右最近邻）对于任意一个数据对象Xj，在满足与其距离小于平均样本距离的限制条件下，数据对象表示与其最邻近的右近邻，数据对象表示与其最邻近的左近邻：

数据对象的最近邻个数包含以下三种情况：

（1）若考察的数据对象既有左最近邻，也有右最近邻，则该数据对象最近邻个数为2。

（2）若考察的数据对象只有左最近邻或者只有右最近邻，则该数据对象最近邻个数为1。

（3）若考察的数据对象既没有左最近邻，也没有右最近邻，则该数据对象最近邻个数为0。

数据对象与其最邻近归属为同一类簇的可能性最大，在聚类过程中，若一个数据对象含有两个最近邻或只含有其中一个最近邻，可以继续考察其最近邻的近邻情况，直到数据对象无近邻或数据对象的近邻全部被标记。

3.3.2 最邻近矩阵与局部密度结合的双重策略

基于密度峰值原则的聚类算法在得到的聚类中心后，直接依据最短欧几里德距离原则进行数据分配，而改进算法引入最邻近矩阵与局部密度结合的双重策略对剩余数据对象进行类簇分配，具体步骤如下。

步骤1根据式（1）～（3）和式（6），计算数据样本集所有数据对象的局部密度，标记局部密度峰点作为第一个初始聚类中心。

步骤2根据式（3）和式（8），选择与局部密度峰点距离小于平均样本距离的数据对象，确定局部密度峰点左、右最近邻。若局部密度峰点包含左、右最近邻或者其一，转步骤3。若局部密度峰点不含有左、右最近邻，转步骤5。

步骤3根据式（4），参考n个数据对象之间的最近邻矩阵Z，分别扫描左、右最近邻所在的行，再根据式（5），确定左、右最近邻的近邻。

步骤4考察左右最近邻的近邻与密度峰值的距离是否小于平均样本距离，若满足条件，将左右最近邻的近邻划分到局部密度峰点的近邻集合中，转步骤3 继续考察其最近邻的近邻情况，若不满足转下一步。

步骤5将该聚类中心与其近邻从数据集中删除，更新数据集。

步骤6检查数据集是否为空，若数据集不为空，继续标记局部密度峰点的数据对象将其作为下一个初始聚类中心，继而转步骤2 并重复上述过程；若数据集为空，代表经过步骤1 到步骤4 已经确定密度峰值点的所有近邻，完成所有数据对象之间的归属关系划分并确定K个聚类中心。

图1（a）是关于原始数据的散点图，图1（b）是对含有19 个样本的数据集基于双重策略构造数据划分后的表现。其中，数据样本集中数据对象1 至数据对象9 所在的空间分布密度较大，数据对象10 至数据对象19 所在的空间分布密度较小，适合考验基于不同种度量的聚类结果。

考虑图1 数据对象9 和数据对象16 的位置，如果仅仅考虑全局分布特点，这两个数据对象周围的密度远远小于其余数据对象的密度，可能在划分过程被单独划分为一类；如果仅仅考虑局部分布特点，数据对象16 与数据对象13 的距离较近，数据对象9 与数据对象8 的距离较近，在划分过程中若误将其归为一类，会导致簇间差异性增大，聚类结果不理想。然而，在综合考虑距离差异值和局部密度的情况下，数据对象16 会对局部密度峰点即数据对象10 影响较大，而数据对象9 对局部密度峰点即数据对象1 影响较小，如图1（b）所示。

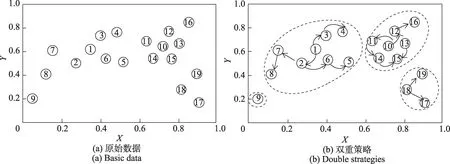
图1 基于双重策略构造数据划分Fig.1 Partition of data under double strategies

3.4 构造最优划分

构造最优划分即通过动态迭代确定最优初始聚类中心，直到聚类中心的位置不再变化，这也标志着改进算法对于这组数据样本点具有收敛性。

定义8（距离均值[14]）数据对象Xi到数据样本集中所有样本点之间的距离均值：

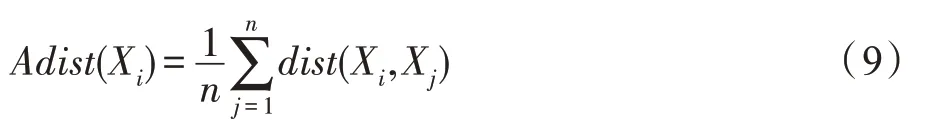
定义9（误差平方和[7]）数据样本集Dn聚类误差平方和：

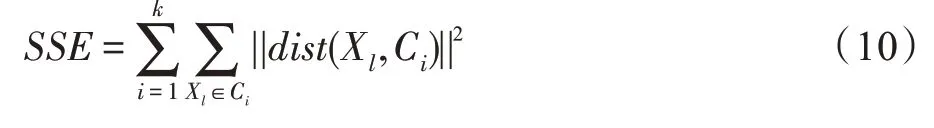
其中，数据对象Xl是属于类簇Ci的样本，SSE表示该数据样本点Xl到聚类中心点Ci的距离平方和。SSE值越小说明聚类效果越优。

改进算法更新初始聚类中心的具体步骤如下：

步骤1根据式（9），分别计算每一个类簇中所有数据样本集的距离均值，并将其更新为该类簇的新聚类中心。

步骤2根据式（10），重新计算当前聚类类簇的误差平方和SSE′，若SSE′＝SSE，表明聚类中心的位置趋于稳定，聚类过程到此结束。否则，令SSE＝SSE′，转向步骤1。

自适应聚类算法流程图见图2。

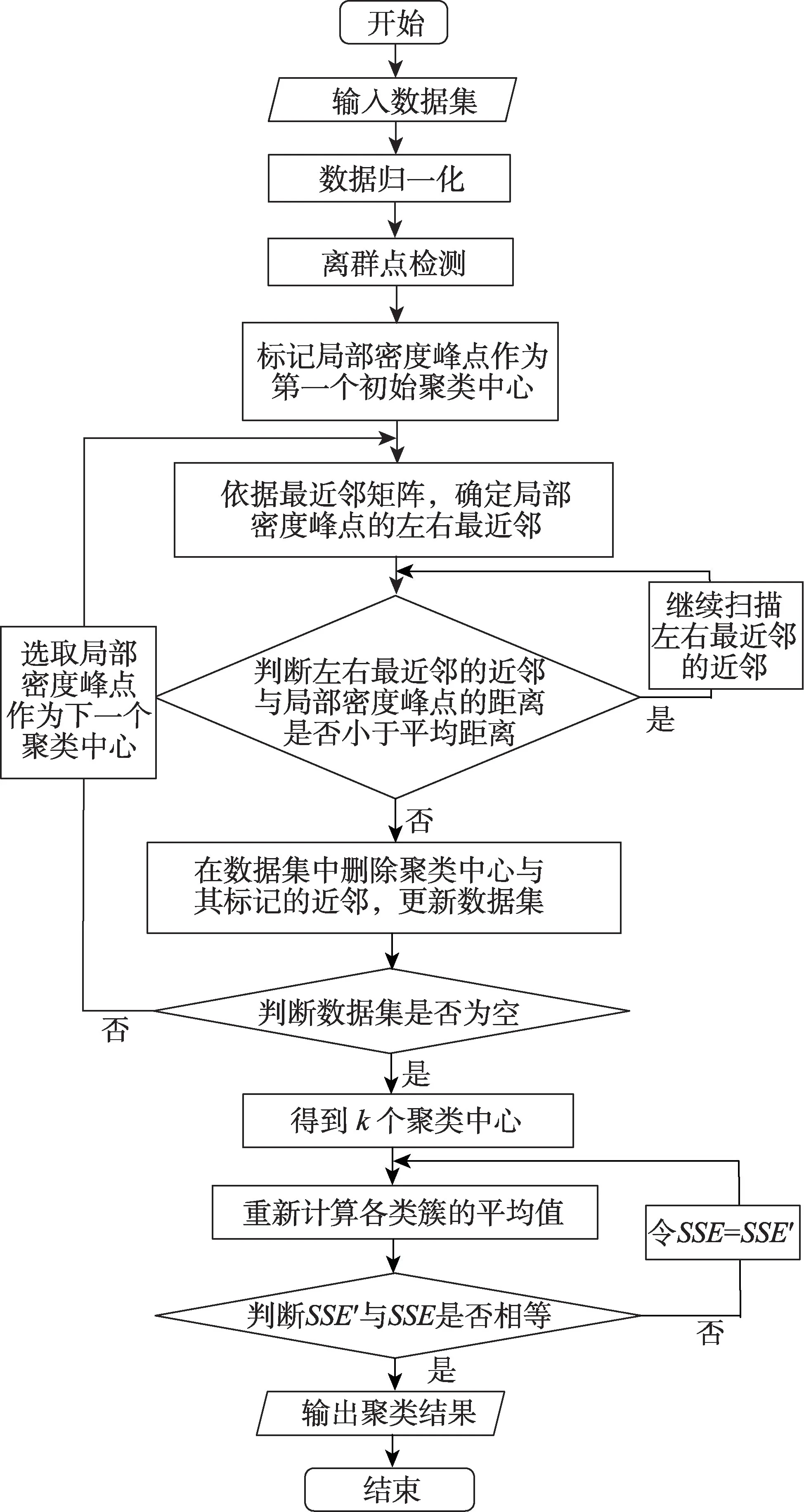
图2 自适应聚类算法流程图Fig.2 Flow chart of adaptive clustering algorithm

4 仿真实验

为了更加准确地测试自适应聚类算法聚类效果的稳定性和有效性，分别在UCI机器学习数据库常用的六个数据集以及人工模拟数据集中进行测试，并把改进算法（表示为算法4）与基于距离的传统Kmeans 算法（表示为算法1）[2]、基于离群点改进的Kmeans 算法（表示为算法2）[6]、基于密度改进的DCCK-means算法（表示为算法3）[19]进行比较。

所有算法的实验环境为：硬件环境为Intel®CoreTMi5-6600CPU，3.30 GHz，8 GB RAM；软件环境为Windows 10 64 位，MATLAB R2016b。

4.1 人工数据集的仿真实验

4.1.1 实验数据

为了更直观地展示改进的动态K-means 算法与其余三种算法的聚类效果，将聚类结果进行可视化处理。本次实验随机生成4 个数值型样本集，它们分布在二维空间中，每个数据样本值都含有两个数据属性，经过归一化处理后的数据样本集特性如表1所示。

表1 人工模拟数据集特性Table 1 Features of artificial dataset

表1 中，数据集Dataset 1 由2 个团状类簇和1 个流形类簇构成，数据集Dataset 2 由5 个椭圆状的类簇构成，数据集Dataset 3 由15 个团状类簇构成，数据集Dataset 4 由7 个相互连接且形状各异的团簇构成，这4 个数据集都含有约5%的离群孤立点，经过归一化处理后的数据样本分布情况如图3 所示，利用不同的颜色表示已知条件下的不同类簇。

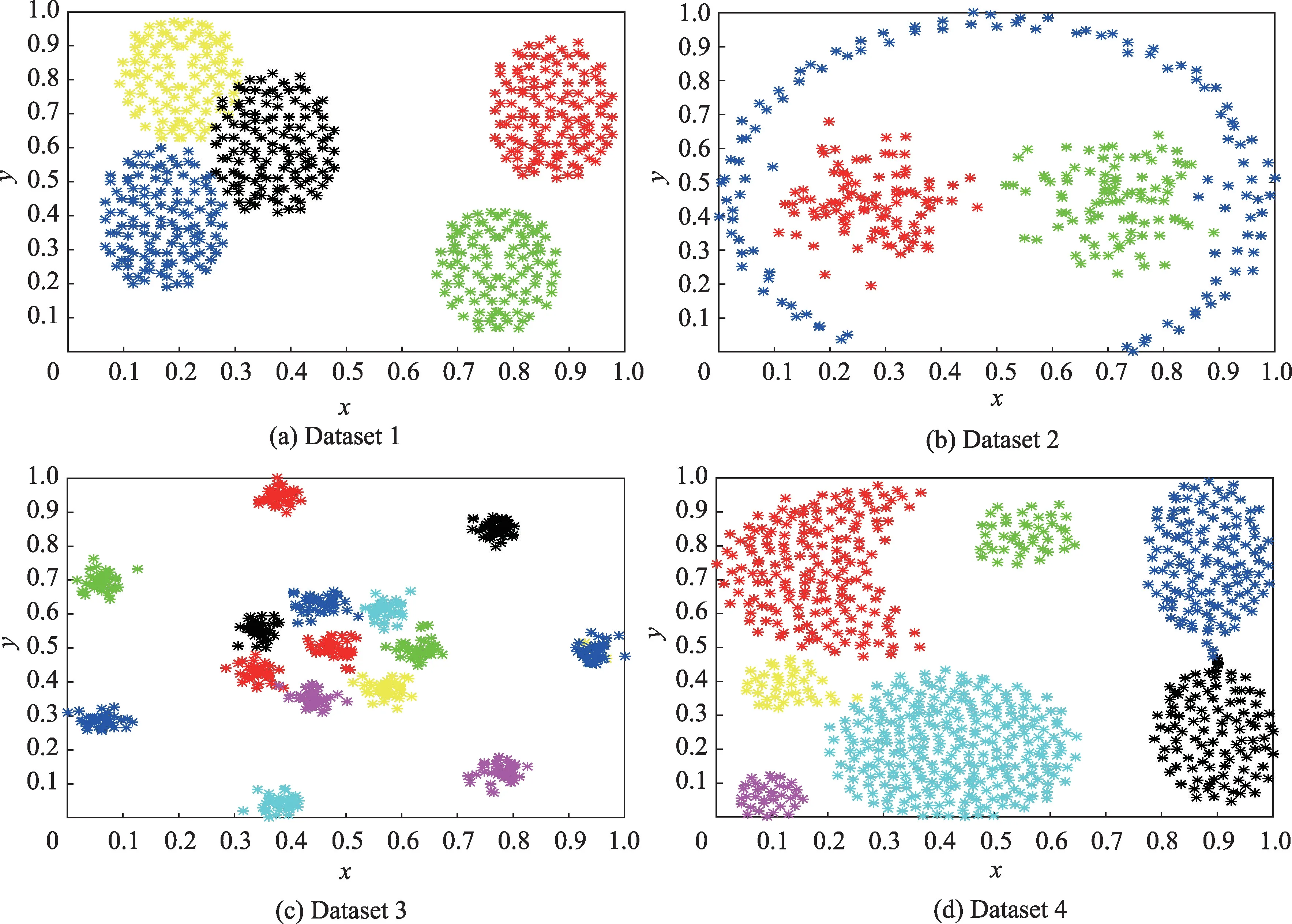
图3 人工数据集分布情况Fig.3 Distribution of artificial datasets

4.1.2 实验参数

对于传统K-means 聚类算法，初始聚类中心的选取具有一定的随机性，这导致准确率与迭代次数的不稳定。因此，对算法1 与算法2 分别运行50 次，取实验结果的平均值进行对比。对于算法3 要设置密度半径与领域最小个数。对于数据集Dataset 1 密度半径设置为0.14，领域最小个数设置为10；对于数据集Dataset 2 密度半径设置为0.2，领域最小个数设置为20；对于数据集Dataset 3 密度半径设置为0.045，领域最小个数设置为17；对于数据集Dataset 4 密度半径设置为0.017，领域最小个数设置为10。改进的自适应聚类算法无需输入任何参数且聚类结果稳定，因此统计一次实验结果即可。

4.1.3 实验结果及分析

图4 至图7 分别对应算法1 至算法4 在人工数据集上得到的聚类结果。需要说明的是，算法4 得到的聚类结果可以以动态形式展示初始聚类中心的确定、数据样本集的划分、数据的迭代次数以及最终的聚类结果。

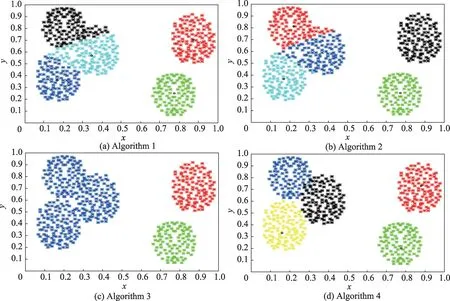
图4 4 种算法在人工数据集Data1 的聚类效果Fig.4 Clustering results of 4 algorithms on artificial Data1

图5 4 种算法在人工数据集Data2 的聚类效果Fig.5 Clustering results of 4 algorithms on artificial Data2

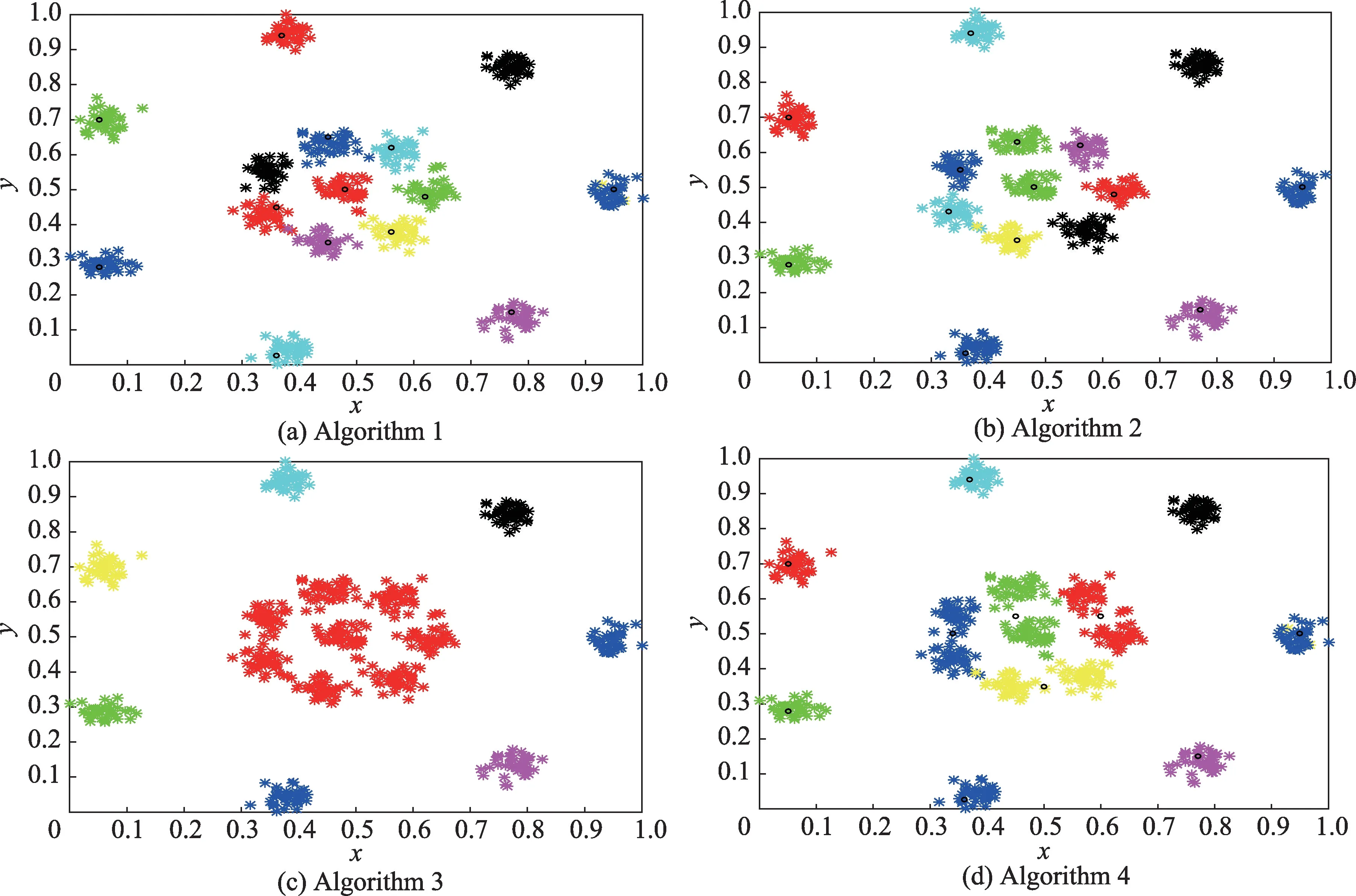
图6 4 种算法在人工数据集Data3 的聚类效果Fig.6 Clustering results of 4 algorithms on artificial Data3

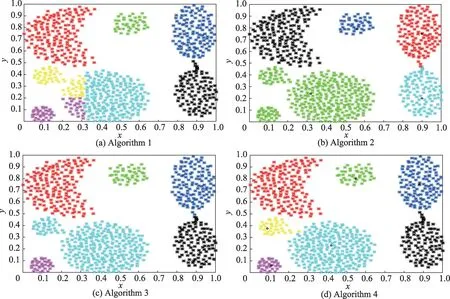
图7 4 种算法在人工数据集Data4 的聚类效果Fig.7 Clustering results of 4 algorithms on artificial Data4

实验表明，算法1 在数据集Dataset 2 和Dataset 3的聚类效果最优，在数据集Dataset 1 和Dataset 4 的聚类效果不太理想，原因是算法1 通过随机选取确定初始聚类中心，离群孤立点对聚类结果的干扰较大，明显降低了聚类结果的准确性，对于分布不均匀的数据集Dataset 1 和Dataset 4 的影响尤其明显。

算法2 对数据集Dataset 3 上的聚类效果最优，在数据集Dataset 4 上的聚类效果最不理想。相比算法3 与算法4，算法2 还是存在随机确定初始聚类中心、人工输入聚类数目的弊端，导致聚类准确率无法得到保障。

算法3 和算法4 整体聚类效果明显优于算法1 和算法2。算法3 在数据集Dataset 2 和Dataset 3 的聚类效果最优，由于数据集Dataset 1 和Dataset 4 分布不均匀且簇类间距离相差较远，导致算法3 不能在聚类过程中有效识别相互连接的团簇，误把部分相邻的两个类簇归为同一类。此外，在聚类过程中算法3 过度依赖于参数的取值，参数一旦设置过大或过小，都会直接影响聚类质量。

从数据集Dataset 2 和Dataset 3 的聚类结果可以看出，由于算法4 充分考虑了距离和密度两个度量因素，聚类效果明显优于单一考虑距离的算法1。从数据集Dataset 1 和Dataset 4 的聚类结果可以看出，算法4 相较于算法3 来说，更适用于处理密度分布不均匀的数据，且不需要依赖参数的取值。

4.2 UCI数据集的仿真实验

4.2.1 实验数据

相较于人工数据集，UCI 数据集[20]属性较多、维数较高且分布不均，聚类难度更高。选择UCI数据集进行测试的优点在于，对于它们的实际划分是已知的，聚类算法的性能可以依据聚类算法得到聚类结果，与已知的真实划分进行比较，进而进行评估。实验所用UCI数据集如表2 所示。

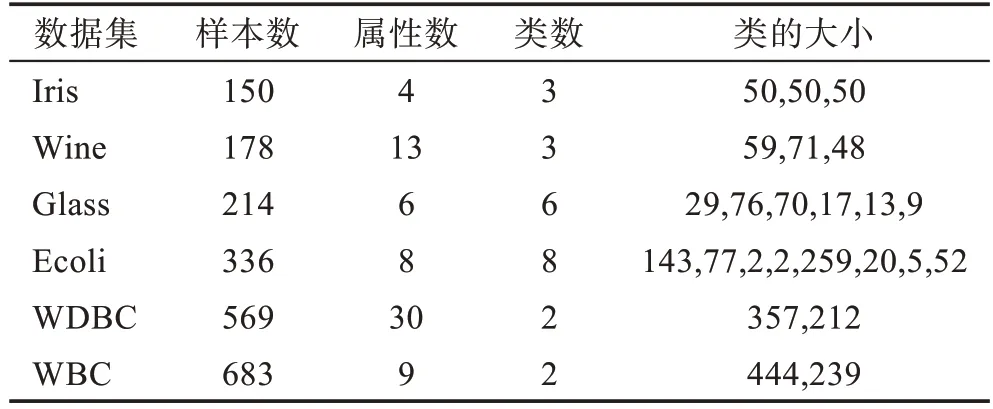
表2 UCI数据集特性Table 2 Features of UCI dataset

4.2.2 聚类性能评价指标

算法聚类效果的评价，除采用常用的聚类准确率作为评价方法之外，选定兰德指数（Rand index）[21]、杰尔德系数（Jaccard coefficient）[22]和调整兰德参数（adjusted Rand index）[23]作为本次实验的评价指标进行比较分析，这三个评价聚类性能的指标是在已知数据样本集正确标签的条件下，对聚类算法得到的划分结果进行评价的有效标准。

由定义可知，兰德指数代表聚类算法得到的聚类划分结果与原始数据集已知的分布之间的匹配度，杰尔德系数代表聚类算法划分的样本对在已知的分布内依然是同一类簇的比率，这三个指标值的范围都在[-1,1]。

4.2.3 实验结果及分析

图8 是将UCI 数据集的已知分类结果（对应数据集左边的柱状图）与改进的自适应聚类算法的聚类结果（对应数据集右边的柱状图）进行直观比较。对同一数据集的一条柱状图进行纵向观察，可以反映数据对象与类簇之间的所属关系。对同一数据集的两条柱状图进行横向比较，如果数据对象在两条柱状图对应的颜色不同，则代表该数据对象通过聚类算法得到的结果与已知的分类结果不同，若数据对象在两条柱状图对应的颜色相同，则代表聚类正确。

图8 UCI数据集聚类正确率比较Fig.8 Comparison of clustering accuracy of UCI dataset

实验表明，改进算法的聚类效果在Iris、Wine、Ecoli、WBC 数据集上表现较佳，而在Glass、WDBC 数据集上的表现一般。原因在于数据集Glass、WDBC的样本个数、属性数目和类别数目明显高于其他数据集，且这两个数据集不同类簇之间的样本差异较小。

需要说明的是，表3 括号内的波动值反映的是算法1 与算法2 平均准确率的区间。表3 关于不同算法的聚类准确率表明，算法1 和算法2 聚类结果的波动较大，而算法3 与改进的动态算法结果稳定，且改进的动态算法相较于其余三种算法在四个UCI 数据集上的准确率最高，其中高出算法1 的平均准确率约20.87 个百分点，高出算法2 的平均准确率约17.66 个百分点。

表3 4 种聚类算法准确率比较Table 3 Accuracy comparison of 4 clustering algorithms

由图9 四种算法关于兰德指数、杰尔德系数以及调整兰德参数的比较显示，算法1 与算法2 的聚类指标值相近，算法3 和算法4 的聚类指标值相近，原因在于算法1 与算法2 仅考虑了距离因素，而算法3 与改进算法都融合了密度因素，且算法4 的兰德指数明显高于剩余三种算法。

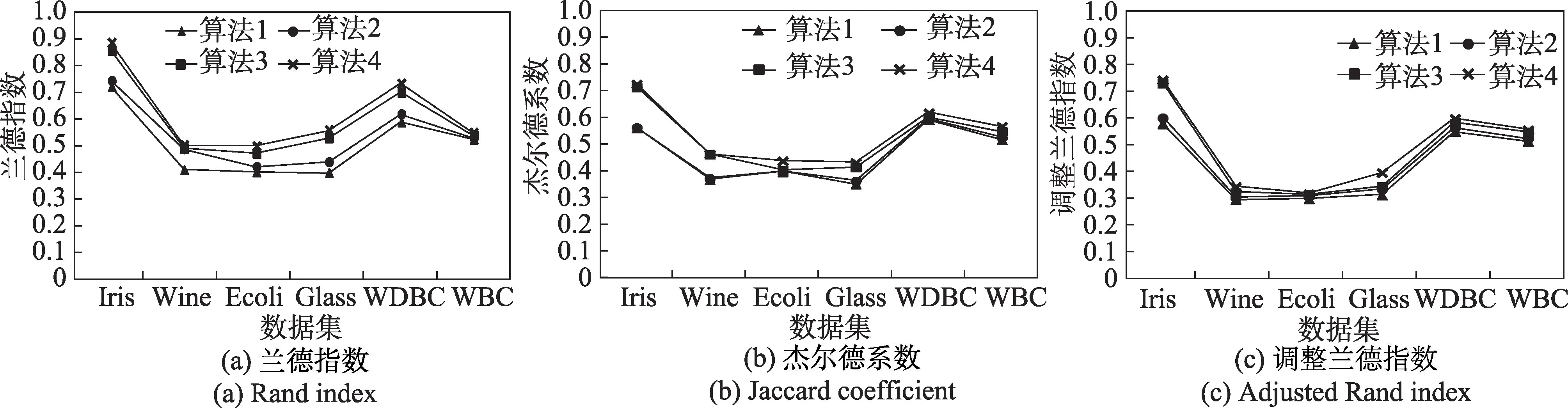
图9 UCI数据集聚类评价指标比较Fig.9 Comparison of UCI dataset clustering evaluation indicators

5 结束语

通过选取含有离群孤立点且分布复杂的二维数据进行动态聚类，在多个维数互异且分布不均的UCI数据集上与基于距离的传统K-means 聚类算法、基于离群点检测改进的K-means 聚类算法以及基于密度的改进的K-means 聚类算法进行对比实验的结果表明：融合最近邻矩阵与局部密度优化的自适应Kmeans 聚类算法，采取最邻近矩阵与局部密度结合的双重策略，自适应确定初始聚类中心的数目及位置的同时，也能对所有的数据对象标记所属类簇，完成数据的初分配。自适应K-means 聚类算法不仅可以考虑全局分布特点，也不会忽略数据对象局部领域内的分布情况。

改进的自适应聚类算法在交替迭代的过程中不仅不需要人工设置聚类数目K值以及其他参数，而且在处理密度分布不均匀数据集时准确率有显著提升。如何简化算法运算以此来高效地处理多维数据将是后续研究的重点工作。