非齐次基因调控网络模型研究综述

张倩倩，胡春玲+，张家瑶，李大伟，邵鸣义

1.合肥学院 人工智能与大数据学院，合肥230031

2.合肥学院 安徽省城市基础设施大数据技术应用工程实验室，合肥230031

在系统生物学中，人们对学习调控网络非常感兴趣，如基因调控转录网络、蛋白质信号转导级联、神经信息流网络或生态网络。首先，了解复杂的基因调控网络对当前的生物医学研究具有重大意义[1]。其次，阐明基因及基因表达产物之间的关系，一直以来都是实验生物学和计算生物学的核心挑战之一[2]。最后，研究基因调控网络的目的在于利用基因表达数据，重现基因间相互作用的拓扑结构，达到揭示基因复杂的作用机理及基因功能信息的目的[3]。

基因调控网络中对转录水平的调控的研究方法主要分为自上而下和自下而上两种策略。其中自上而下的策略是利用数学建模方法和系统生物学知识，分析基因表达数据，从而重构基因调控网络，这也是目前比较常用的构建基因调控网络的方法。目前针对基因调控网络建模发展了很多数学模型，例如布尔网络模型[4-5]、线性回归模型[6-7]、微分方程模型[8-10]和贝叶斯网络模型[11-13]等，其中贝叶斯网络模型就是被广泛使用的一种建模工具。

为了阐明调控网络结构，可以使用基于贝叶斯网络的机器学习方法，这是Friedman 等人于2000 年在一篇开创性的论文中提出的，Friedman[14]利用贝叶斯网络（Bayesian networks，BN）构建了一个包含800 个基因的基因调控网络。但是，两个基因之间的调控存在一定的时延，Murphy 等人[15]根据这一特性首次提出用动态贝叶斯网络（dynamic Bayesian networks，DBN）模型分析时序基因表达数据以及构建基因调控网络，此方法一经提出，许多学者展开了更多的研究[16-24]。据了解，传统DBN 模型的标准假设是：观察到的时间序列是满足齐次马尔可夫过程的，属于平稳时间序列。但是，这种过于严格的标准可能会导致错误的推断结果。因为在系统生物学的实际应用中，调节相互作用往往是随时间而变化的，例如会受到环境或实验条件变化的影响。也就是说，实际上的时间序列一般是非平稳的。因此，针对这种非平稳基因时序数据，Grzegorczyk 等人这些年做了很多研究，提出了一系列非齐次动态贝叶斯网络（non-homogeneous dynamic Bayesian network，NHDBN）模型[25-35]。研究表明，NH-DBN 模型对于基因调控网络的学习主要分为三部分：一是网络推断；二是时间片段的划分；三是网络结构的参数学习。

本文梳理了基于齐次动态贝叶斯网络的基因调控网络建模方法，并将非齐次动态贝叶斯网络（NH-DBN）模型划分为图1 所示的两大类，分别进行了分析和比较。最后，探讨了基因调控网络构建的困难和挑战。

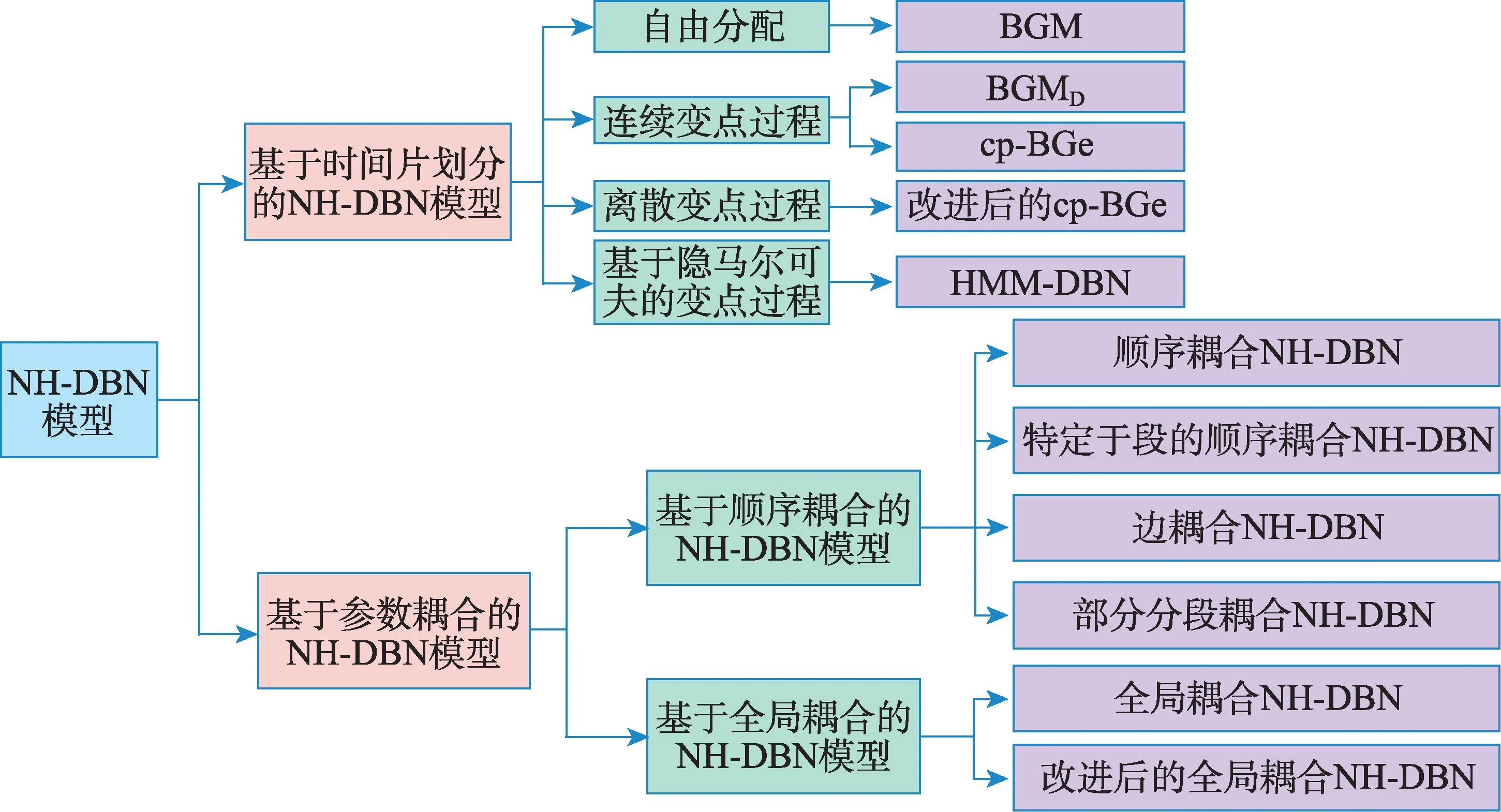
图1 非齐次动态贝叶斯网络模型分类Fig.1 Classification of non-homogeneous dynamic Bayesian network models

1 基于齐次DBN 的基因调控网络建模方法

在重建基因调控网络（gene regulatory networks，GRN）时，DBN 是最常用的推理模型之一。DBN 实际上是BN 在时序过程建模领域的拓展，它打破了BN 的限制，能够实现循环网络的构建。

在时间序列数据建模中，一组随机变量的值在不同时间点被观察到。这是通过将变量的状态按时间点划分来完成的，如图2 所描述（上图表示包含一个周期x1→x2→x4→x5→x1的网络结构。下图表示DBN 通过将变量的状态按时间点划分来描述这个周期）。一般来说，时间序列数据上的DBN 设计是单向的，即网络应该在时间上向前流动。假设每个时间点都是单一变量Yi，一连串数据{Y1,Y2,…,Yt}的最简单因果模型将是一个一阶马尔可夫链，其中下一个变量的状态只依赖于前一个变量。这个序列的联合概率分布的一般形式是：

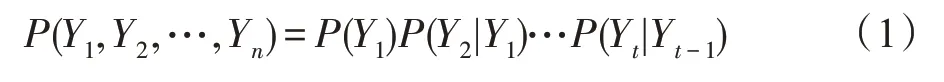
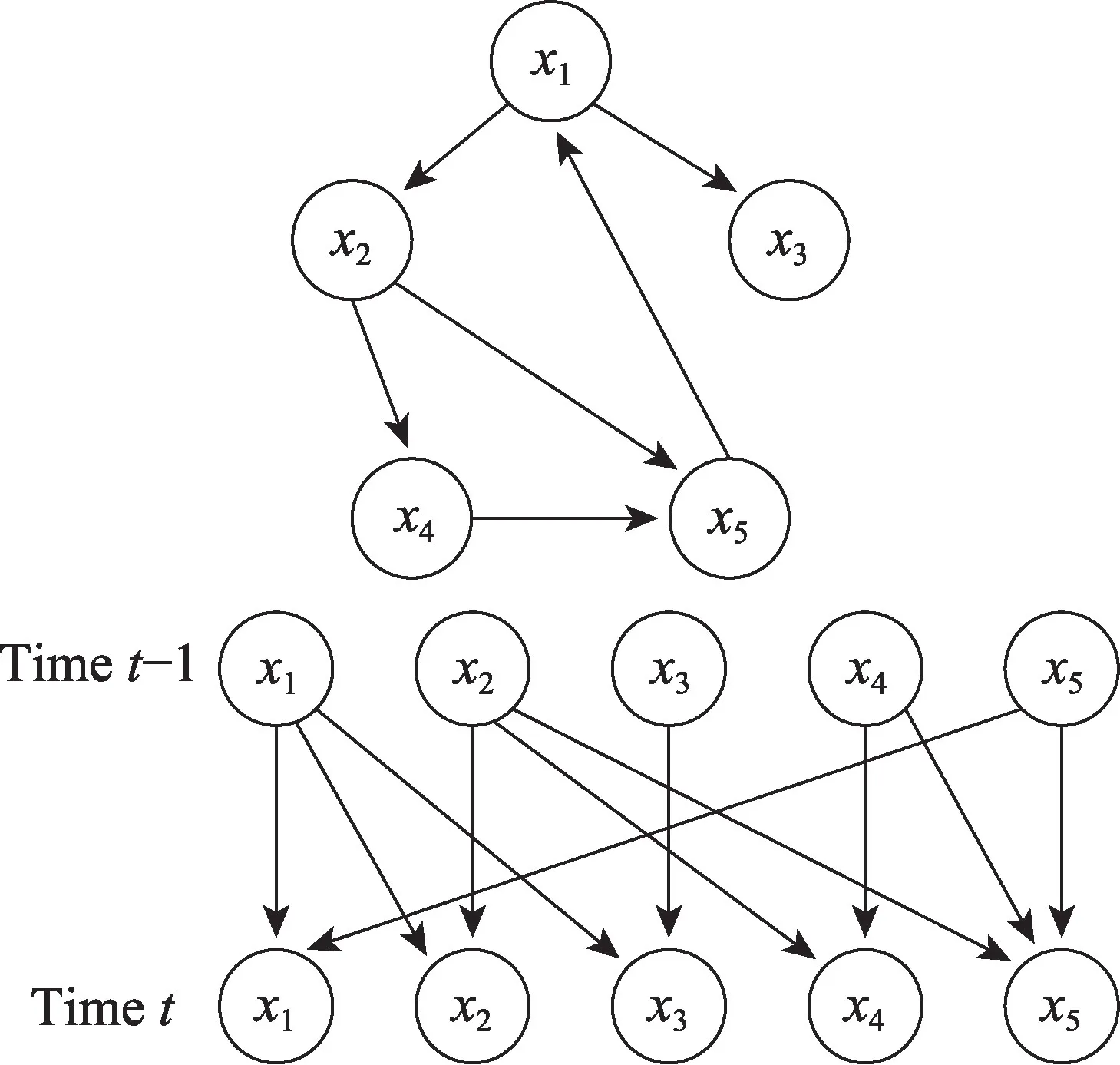
图2 DBN 的示意图Fig.2 Schematic diagram of DBN

许多生物途径，如信号通路和调控通路，在本质上是循环和动态的，因此证明使用DBN 从时间序列表达数据中推断出GRN 是可行的。DBN 建模通常遵循BN 类似的步骤，假设有i个微阵列，测量j个基因的表达水平。微阵列数据集可以概括为i×j矩阵X=(x1,x2,…,xi)，其中每一行向量xi=(xi1,xi2,…,xij)对应于在时间t测量的基因表达向量。首先，在DBN建模中假设时间依赖性。这种关系被描述为一个有向无环图（一阶马尔可夫链），其中只允许有向前的边。根据式（1），联合分布概率可以分解为：

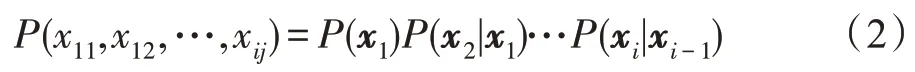
接下来，根据条件概率P(xi|xi-1)的构造对基因调控进行建模。假设网络结构在所有时间点上都是稳定的，则条件概率可以分解为每个基因的条件概率的乘积，当给定其父基因时：

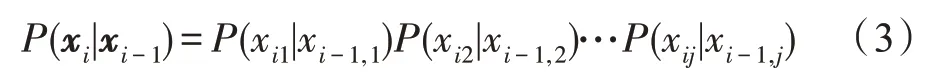
通过这种方式，DBN 实现了对循环路径的建模。DBN 能够将数据本身的特点与实际问题的时序信息有机地结合起来，用来表示多样化的时序信息，如具有复杂结构关系、因果关系或不确定性的关系。因此，DBN 更适合于描述时间序列的基因表达数据。

当前有很多工作是利用DBN 从表达数据中建模基因调节网络。Ong 等人[36]提出了DBN 的最早应用之一，即从时间序列基因表达数据推断GRN。主要研究目标是利用先前的生物知识和时间序列基因表达数据来模拟基因之间的相互作用和关系。作者提出了一种基于DBN 的方法，该方法通过结合操作子图和当前的观察来提高结果的质量。首先，DBN 被应用于大肠杆菌色氨酸代谢的时间序列基因表达数据。然后在以往工作中采用的操作子图的帮助下，建立一个初步的DBN 结构来识别操作子和目标基因之间的关系。下一步是利用领域专家知识来重新设定操作子之间的影响概率。初始概率是从领域专家那里获得的Dirichlet 先验。结果显示，DBN 和先验生物学知识的结合在推断大肠杆菌色氨酸代谢时间序列基因表达数据的GRN 方面是有效的。与传统方法相比，所提出的方法能够提供一个更全面的色氨酸代谢网络视图。

Perrin 等人[37]指出，在建立基因相互作用模型时有两个问题：学习网络结构和识别所有功能参数。为了同时解决这两个问题，作者提出了一个基于DBN 的框架，在扩展的最大期望（expectation-maximization，EM）算法的基础上进行惩罚性似然最大化。使用EM 算法学习参数，该算法由期望和最大化阶段组成。第一阶段使用一系列的过滤器和平滑器过程来定义模型参数。第二阶段关注的是计算一个新的期望阶段的梯度步骤。每个EM 步骤的惩罚似然都会增加，直到达到局部最大值。此外，EM 算法为该模型提供了处理基因表达数据中发现的缺失值的能力。为了评估结果，将该模型应用于大肠杆菌修复网络基因表达数据。所提出的模型成功地恢复了网络中98%的连接，并证明了该模型在捕捉基因-基因相互作用方面的能力。

Tamada 等人[38]观察到，与网络模型中的基因数量相比，微阵列的数量不足，这阻碍了推断的准确性。为了解决这个问题，作者将启动子元素检测与DBN 结合起来。首先使用DBN 构建了一个初始网络模型，然后将几个假定为转录因子的候选基因作为父基因，并且定义了潜在的受控基因组。启动子元素检测是基于这样一个生物学事实：如果一个父基因是一个转录因子，它的子基因可能在其DNA 序列的启动子区域共享一个共识图案。该方法根据估计的网络结构来检测共识图案，然后用图案检测的结果重新估计网络。该模型反复进行，直到网络变得稳定。作者评估了他们提出的模型，首先将其应用于伪微阵列数据和蒙特卡洛模拟产生的DNA 序列。他们还将该模型应用于S.cerevisiae 的基因表达数据。结果显示，在这两种情况下，该模型能够比以前的方法推断出更准确的GRN，这是因为动机信息能够修正不正确的基因关系。

Zou 和Conzen[39]开发了一种基于DBN 的方法，该方法通过潜在调节器选择和时滞估计来提高推断的准确性和计算速度。作者指出，传统的DBN 通常将数据集中的所有基因都看作某个目标基因的潜在调控因子，从而导致搜索空间大，计算成本高。此外，DBN 缺乏处理生物相关转录时间滞后的能力，因此导致推断准确性低。作者旨在解决这两个问题：首先，通过限制基于表达变化的潜在调节器的数量来减少搜索空间的大小；其次，根据潜在调节器和目标基因的初始表达变化之间的时间差来实施时间滞后估计。所提出的模型被应用于S.cerevisiae 细胞周期时间序列基因表达数据，与传统的DBN 相比，它在准确性和计算速度方面有明显的性能改进。

Dojer 等人[40]通过将DBN 与扰动相结合，推断出了更可靠的GRN，因为扰动的表达数据能够提供对于基因关系和因果关系有意义的信息。基因表达首先被特定的处理方式所扰乱，如基因敲除实验和环境压力，因此改变了相互作用的性质。然后，通过替代被扰乱基因的mRNA 的微分方程，将扰乱引入模型。在学习过程中，表达水平被离散化，阈值为0.5。引入阈值的目的是为了减少离散化引起的表达的低变异性。结果显示，由于扰动的表达数据，推断网络的质量有了明显的提高。

Wu 和Liu[41]旨在研究从微阵列实验产生的高维基因表达数据中对GRN 进行DBN 建模的可行性。作者着重于通过使用两种不同的网络结构搜索方法来改进DBN 建模。GSR（greedy hill-climbing search with restarts）和马尔可夫链蒙特卡洛（Markov chain Monte Carlo，MCMC），这两种方法都被应用于DBN建模，以减少基因表达数据的维度问题。就GSR 而言，具有最高分的初始网络结构可以通过增加或删除一条边来进行可能的突变。然后，变异后的网络模型被设定为新的基础网络结构。这个过程反复进行，直到达到局部最大值。最终的网络结构将被保存，并开始新的运行。反之，MCMC 方法与梅特罗波利斯-黑斯廷斯（Metropolis-Hastings，M-H）算法相结合。一个新的候选模型将从基于当前模型的跳跃分布中产生。随后计算候选模型的接受概率，以确定候选模型是应该被拒绝还是接受。通过模型平均技术分析了两种搜索方法的性能。基于这些结果，作者认为两种方法在时间效率方面具有可比性，但与GSR 相比，MCMC 取得了更好的预测精度。

表1 将以上动态贝叶斯网络模型进行对比分析并进行了归纳总结。

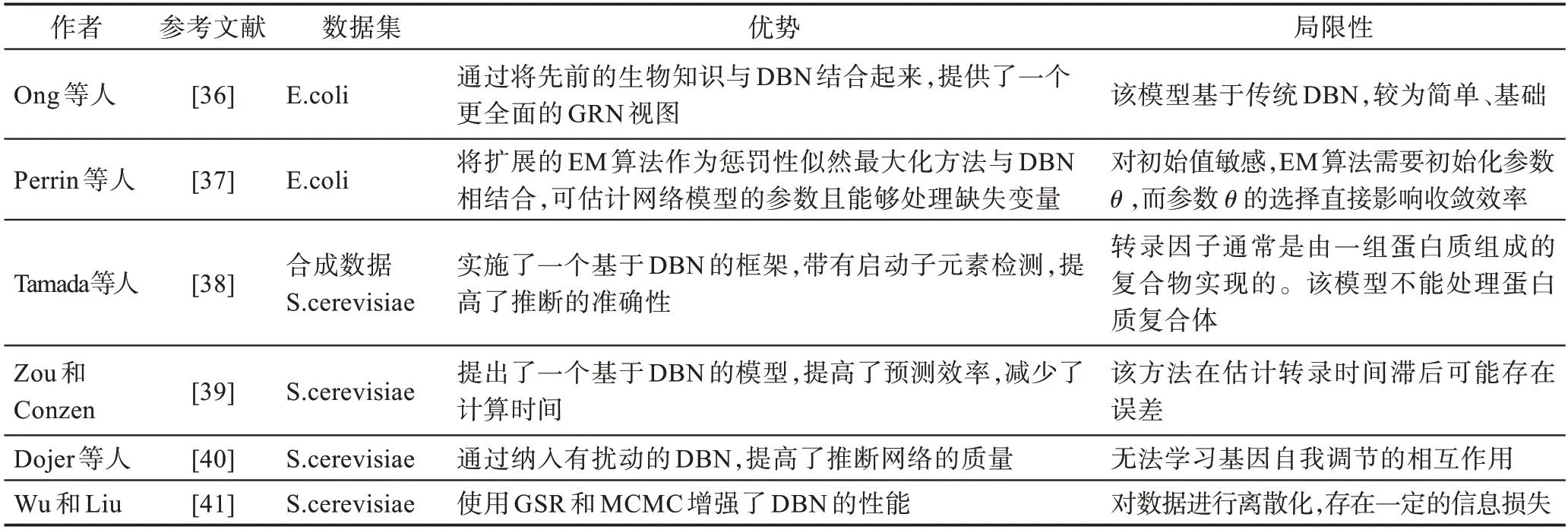
表1 基于齐次DBN 的基因调控网络建模方法比较Table 1 Comparison of gene regulatory network modeling methods based on homogeneous DBN

传统的DBN 在建模时间序列时基于齐次约束，该约束要求被建模时间序列的分布随着时间的推移而保持稳定。在上述齐次假设的基础上，传统DBN的建模能力受到了极大的约束，实际中的诸多场合不符合苛刻的齐次要求。例如，果蝇基因调控网络的拓扑结构会随着果蝇的生长而发生改变。基于上述原因，亟需新的高效模型建模上述场景中的非稳态数据。在这样的背景下，非齐次动态贝叶斯网络被提出。

2 基于时间片划分的NH-DBN 模型

NH-DBN 模型处理的一般是时序数据，此类模型处理时序数据的关键步骤则是划分时间片段。随着技术的发展，时间片的划分方式也得到了逐步提升，本段主要介绍了基于以下四种方法的相关模型：自由分配、连续变点过程、离散变点过程以及基于隐马尔可夫的变点过程。

2.1 基于自由分配的NH-DBN 模型

Grzegorczyk 等人于2008 年[25]提出了一种基于贝叶斯网络的模型来建模基因调控网络。该模型在段之间保持推断出的网络结构不变，每个段使用贝叶斯网络的高斯BGe 模型独立建模，被称为BGM 模型。该模型基于高斯混合贝叶斯模型，使用潜在变量将单个观测值分配到不同的类别。然后利用MCMC 方法从后验分布中对网络结构、时间片的数量和潜在变量分配进行采样，并使用文献[42]提出的分配采样器作为可跳逆的马尔可夫链蒙特卡洛（reversible jump Markov chain Monte Carlo，RJMCMC）采样[43]的替代方法。关于时间片的划分，该模型则采用了较为简单的自由分配，将数据点自由分配给状态，随机确定时间片段。

2.2 基于连续变点过程的NH-DBN 模型

2.2.1 BGMD 模型

Grzegorczyk 等人[26]在2009 年对文献[25]的BGM模型做了进一步研究，作者提出了一种新的动态贝叶斯网络方法来模拟非平稳和非线性的动态基因调控过程，该模型被称作BGMD模型。新方法基于多变点过程和BGM 模型，同样是使用潜在变量将单个测量值分配给不同的时间片，但是对于时间片的划分方式发生了变化，由于自由分配太有随机性，对于时间片的划分不够准确。虽然自由分配具有普适性，但它不能利用与时间过程相关的特定先验知识。BGMD模型使用连续变点过程的方法，该方法结合了先验知识，即在一个时间序列中，相邻的时间点很可能被分配给相同的类别，与BGM 模型类似，变化点的数量和位置同样是利用MCMC方法从后验分布采样。

2.2.2 cp-BGe模型

Grzegorczyk 等人[27]于2009 年提出了一种用于连续数据的非均匀动态变点BGe（changepoint-BGe，cp-BGe）模型，该模型基于文献[25]、文献[42]和文献[44]的工作。同样是用连续变点过程代替了文献[25]中的自由分配模型，但同时也引用了文献[44]中的特定于节点的变点的概念，与其不同的是，作者不使用贝叶斯信息准则（Bayesian information criterion，BIC）作为近似评分函数，而是计算关于该模型网络结构的边际似然来近似评分。在该方法中，参数允许在不同的段之间变化，并且在同一网络结构中提供了不同的段之间的基本信息共享。该模型在参数方面是非平稳的，而网络结构在段之间保持不变。该模型实际上同样是BGe 模型的混合，也被称为非平稳BGe模型。

2.3 基于离散变点过程的NH-DBN 模型

Grzegorczyk 等 人[28]于2011 年 对cp-BGe 模 型 进行了进一步的改进，提出了一个新的非均匀动态变点BGe（new changepoint-BGe，New cp-BGe）模型。首先新模型采用了一个新颖的离散变点过程，替代了之前的连续变点过程。它们的不同点主要在于，在连续变点过程中，变化点独立且均匀分布在一个连续区间上，而在离散变点过程中，变化点独立且均匀分布在一个离散区间上，且在离散变点过程中，实现了分配向量和变化点之间的一对一映射。其次，新模型还提出了新的MCMC 方案，即引入了一种新的父节点翻转移动。父节点翻转移动是指将当前父节点集合πn中的一个父节点Xi∈πn交换成另一个新节点Xj∉πn。最后该模型也解决了文献[45]和文献[46]提出的NH-DBN 模型的两个缺点：（1）数据使用时要进行离散化，会导致固有的信息损失。（2）不同的网络结构与不同的时间序列段相关联，这对于短时间序列将不可避免地导致过度拟合或夸大的不确定性推断。解决方案如下：（1）新模型的数据在使用时是连续的，不需要进行离散化处理，避免了第一个问题。（2）新模型的参数是变化的，而所有段的网络结构都是相同的。虽然在某些情况下（比如形态发生）这个模型的局限性太大，但是对于大多数时间尺度较短的细胞过程来说，随着时间变化的不是结构，而是调节相互作用的强度。

2.4 基于隐马尔可夫的变点过程的NH-DBN模型

Grzegorczyk 于2016 年提出的基于隐马尔可夫的非齐次动态贝叶斯网络（non-homogeneous dynamic Bayesian network with hidden Markov model，HMMDBN）模型[29]，同样是假设推理过程中不同时间片段的网络结构是固定的，变化是其回归参数。该模型最大的改进之处在于假设时间数据点的底层分配遵循隐马尔可夫模型。HMM-DBN 模型是与多转换点过程相结合的动态贝叶斯网络（DBN with changepoints，CPS-DBN）模型和混合动态贝叶斯网络（MIXDBN）模型的结合。CPS-DBN[27]将时间序列划分为多个时间片段后，对于不同片段内的数据点要被分配给对应相同的状态，但是不同片段的数据点必须分配给不同的状态（即变点过程）。MIX-DBN[25]允许将数据点无限制地自由分配给状态，但是没有考虑到数据点的时间顺序（即自由分配）。该论文提出的HMM-DBN 模型既考虑到了数据的时间顺序，也没有对数据点的分配状态施加任何限制。

然后作者提出了关于转换点采样的两对新的移动方案：第一对是包含和排除移动；第二对是出生和死亡移动。这改善了分配采样器的混合和收敛性。图3 以及图4 展示了包含移动和出生移动的操作示例。

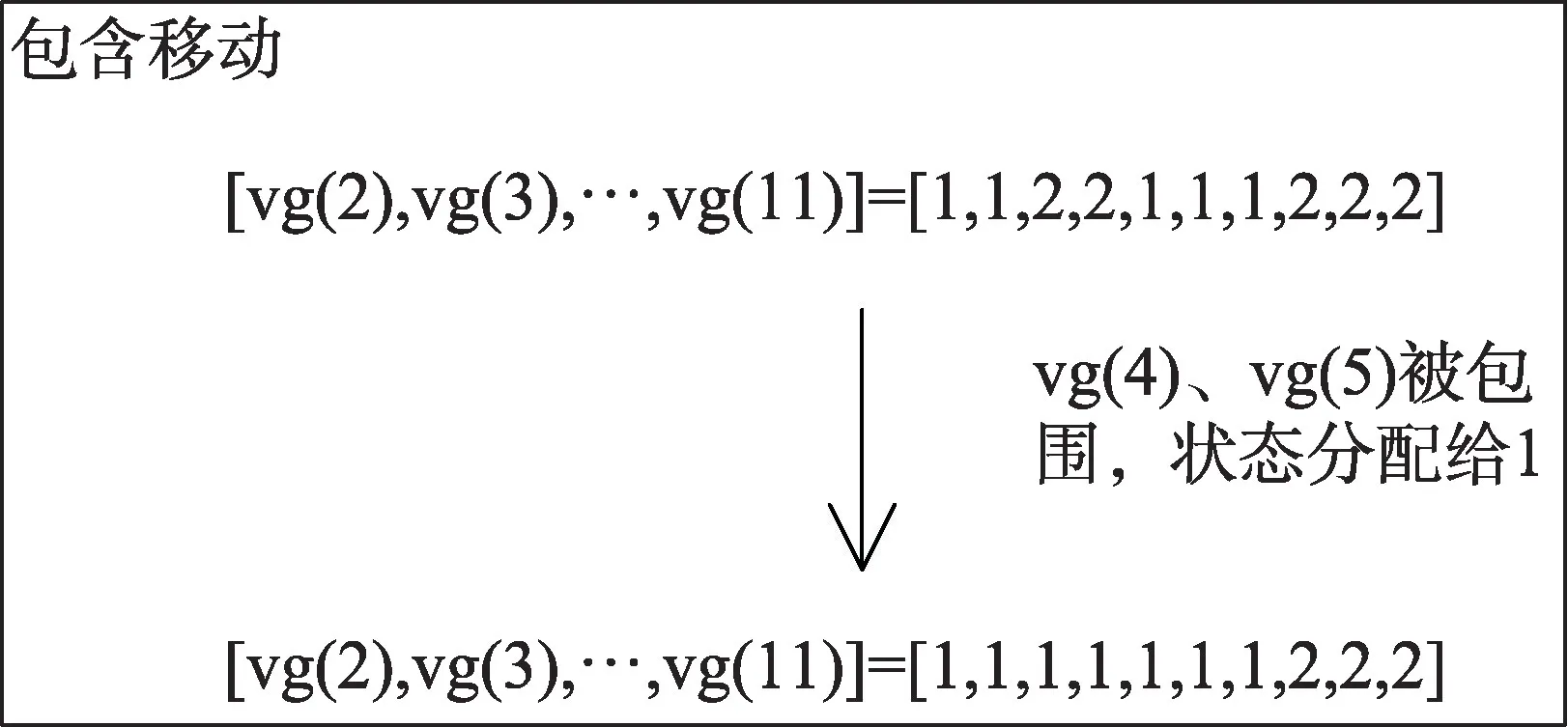
图3 包含移动Fig.3 Inclusion move

图4 出生移动Fig.4 Birth move

表2 从改进措施、模型优势和局限性方面，对本节描述的基于时间片划分的非齐次动态贝叶斯网络模型进行了归纳总结。

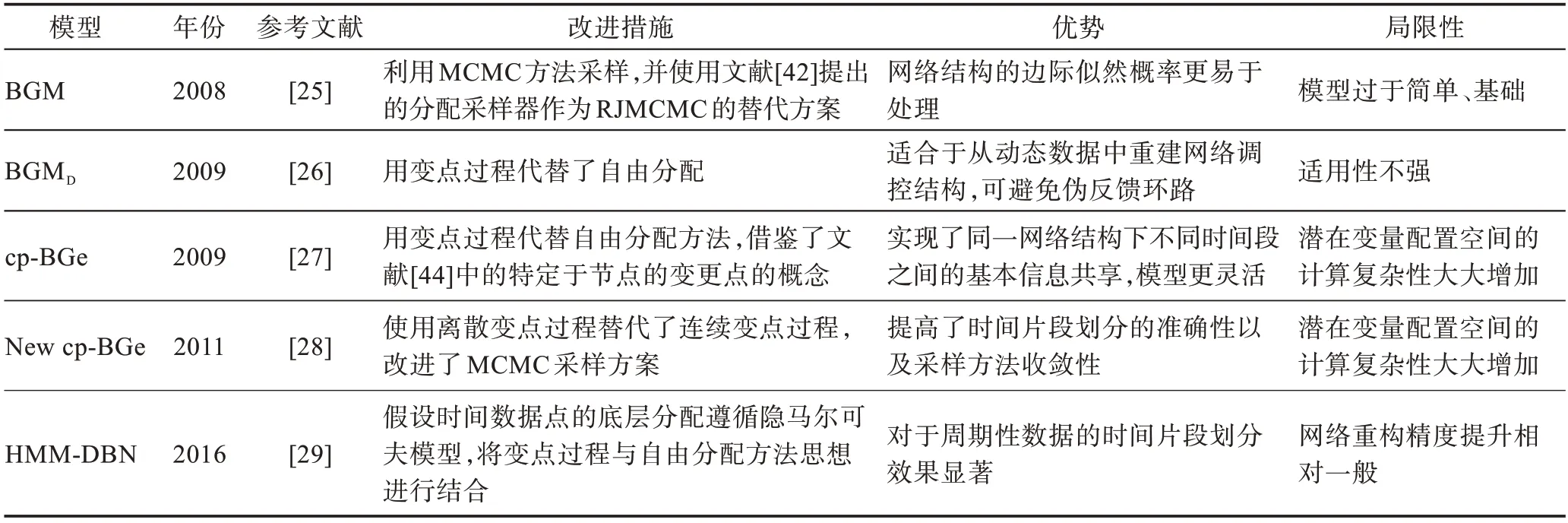
表2 基于时间片划分的NH-DBN 模型比较Table 2 Comparison of NH-DBN models based on time slice partition

3 基于参数耦合的NH-DBN 模型

相关文献表明[25,27-29]，为了更好地进行网络推断，假设在不同时间段内网络结构是保持不变的，变化的只是调节作用强度，那么学习网络结构的相关调节作用强度参数就格外重要。因此，对于基因调控网络的参数学习方面，Grzegorczyk 等人从2012 年到2021 年提出了六种基于参数耦合的NH-DBN 模型，参数耦合方式总的来说分为顺序（序列）耦合[30-33]和全局耦合[34-35]两大类。

3.1 顺序耦合NH-DBN 模型

由于基因表达时间序列过短，以往模型在推断过程中过于灵活，会导致过拟合或夸大的不确定性推理。为解决这个问题，Grzegorczyk 等人于2012 年提出了具有顺序耦合非齐次动态贝叶斯网络（sequentially coupled NH-DBN，SC NH-DBN）模型[30]。该模型引入了一个时间片段之间共享的顺序耦合参数，它本身是从数据中推断出来的。顺序耦合参数的引用使得模型实现了各段的回归参数的推断不再是独立的，而是使用耦合参数调节回归参数的耦合强度（即回归参数的相似性）。实际上，假设在相邻的时间间隔内，大自然重新发明了调节网络是不现实的。因此，作者假设任何时间段上的相互作用强度总体上与前一个时间段上的强度相似。该模型主要实现了以上想法以及对采样方案进行了一些调整。该模型的采样方案如下（如图5 所示）：（1）网络推断。随机选择一个单边操作移动（删除边、添加边或翻转边）并执行M-H 方法采样出父节点集。（2）分段更新。如果选择的变更点是固定的就跳过此步骤；否则，随机选择一个变点诞生、死亡或者重新分配并且执行M-H 方法采样出一个新的变更点集。（3）超参数的更新。使用折叠Gibbs 采样步骤重新采样超参数，通过相关概率公式进行这4 个参数——信噪比超参数δg、回归参数wg,h、顺序耦合参数λg以及方差超参数σg的迭代采样。

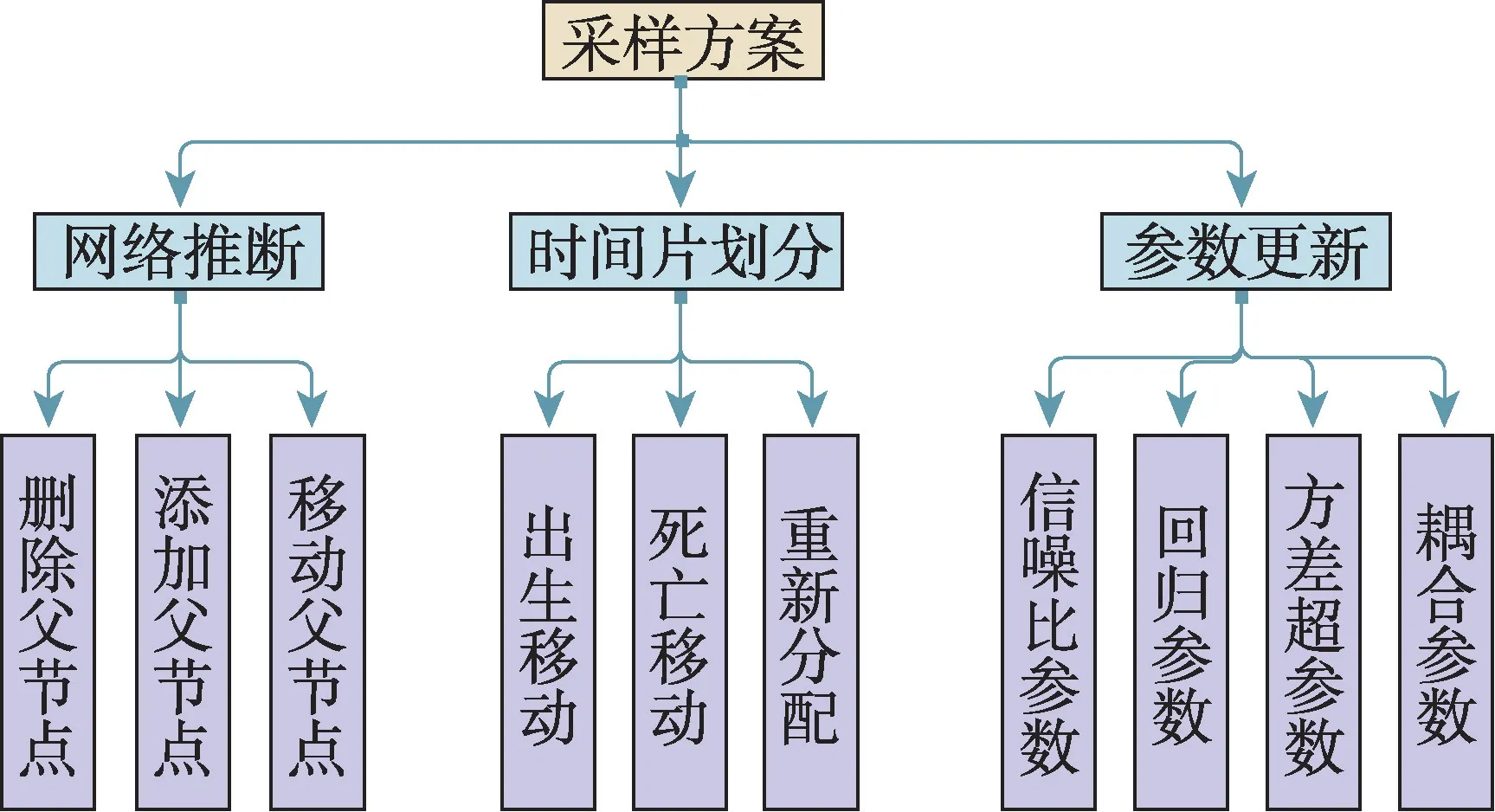
图5 顺序耦合NH-DBN 模型的采样方案Fig.5 Sampling scheme of sequentially coupled NH-DBN model

Grzegorczyk 等人于2012 年提出的SC NH-DBN模型虽然有一定的提升，但也存在一个缺点，即在2012 年的模型中，通过将第h+1 段中的耦合参数的先验期望设置为来自第h段的耦合参数的后验期望，最终会导致所有相邻的段具有相同的耦合强度。Kamalabad 等人于2018 年提出了一个新的改进后的顺序耦合模型，称为特定于段的顺序耦合非齐次动态贝叶斯网络（segment-specific sequentially coupled NH-DBN，SSC NH-DBN）模型[31]，在文献中也被称为M1,1模型。改进之后的模型对于每对相邻的段，存在特定于段的耦合参数，参数之间的耦合强度可以随时间变化。段特定的耦合参数从段内的数据点推断出来，后一段的耦合强度依赖于前一段的耦合强度和当前段数据潜在信息，这大大增加了模型的准确性。

由于2019 年之前提出的顺序耦合模型都有一个缺点，即它强制耦合，不能解除耦合，Kamalabad 和Grzegorczyk 于2019 年和2021 年提出了两个新的模型，一是可以判断边是否耦合，二是可以判断时间段是否耦合。不同于以往的模型强制全部耦合或全部不耦合，这种部分耦合部分不耦合的情况更符合现实情况，对于重构精度可以达到明显的提高。Mahdi等人于2019 年提出了一个新的NH-DBN 模型，称为边耦合非齐次动态贝叶斯网络（edge-wise coupled NH-DBN，EWC NH-DBN）模型[32]。它的主要优点在于结合了非耦合NH-DBN 和耦合NH-DBN 的特征。对于每一条边，该模型可以推测出它的回归系数是应该耦合还是应该保持不耦合。为了区分出回归系数的耦合性，作者引入了一个指标向量，其元素为二进制变量，当其元素值为1 时，表示对应的回归系数是耦合的，当为0 时，表示回归系数不耦合。

Kamalabad 等人于2021 年提出了一个部分分段耦合非齐次动态贝叶斯网络（partially segment-wise coupled NH-DBN，PSC NH-DBN）模型[33]。该模型可看作一个非耦合模型和完全耦合模型（完全耦合模型不同于全局耦合模型，完全耦合模型主要是强调全部段都强制耦合）的结合。与文献[32]的模型类似，同样是提出了一个离散二元指标向量δh，其元素值为1 时，表示当前段h与前一段耦合，其元素值为0时则代表分离。不同点在于，该模型用部分耦合时间段的概念取代了部分耦合边缘的概念。该模型可以达到两个极限：当所有段都耦合时（h>2 时，δh=1），即为完全耦合模型；如果把所有段都解除耦合（h>0 时，δh=0），则称为非耦合模型。

3.2 全局耦合NH-DBN 模型

由于采用顺序耦合方法，信息只能在相邻段之间共享，它比较适用于系统的发育过程。比方说，当一种昆虫经历其生命周期的不同阶段时，人们就会认为，距离近的阶段（如幼虫和胚胎）比距离远的阶段（如幼虫和成虫）有更多的共性。那么在时间序列片段受不同实验场景或环境条件影响的情况下（例如，当一个酵母菌株暴露于不同的碳源，如葡萄糖、半乳糖和果糖），信息共享没有自然顺序，这些片段很多被视为可互换的。为解决这种情况，Grzegorczyk 等人[34]于2012 年提出了全局耦合非齐次动态贝叶斯网络（globally coupled NH-DBN，GC NH-DBN）模型，全局耦合即是指时间片段被视为可交互的，信息被全局共享。Grzegorczyk等人于2012年首次提出了全局耦合的相关概念，模型不够成熟。于是Grzegorczyk 等人[35]于2013 年对文献[34]提出的方法进行了以下改进：一是对文献[34]的模型进行了扩展，在模型层次中引入了一个额外的层，允许网络节点之间的信息共享（Grzegorczyk 等人2012 年提出的两篇关于顺序耦合和全局耦合的文章都不允许网络节点之间信息共享[30,34]），并对噪声方差超参数的各种耦合方案进行了比较。二是引入了一种新的折叠Gibbs 采样方法，它取代了文献[34]中的MCMC 算法中效率较低的非折叠Gibbs 采样方法。三是最重要的一部分，展示了如何使用折叠和阻塞技术来开发一种新的先进的MCMC 算法。提出的全局耦合NH-DBN 模型在网络节点之间的信息共享上进行了研究。在文献[34]的模型中每个节点的超参数在原始模型中是独立建模的，在扩展模型中，将各节点的噪声方差和各时间段交互参数之间的耦合强度进行分层耦合，即增加二级超参数。为了在片段之间引入信息共享，作者在贝叶斯层次结构中添加额外的层，并假设回归参数的均值向量服从共轭高斯先验分布。

表3 从改进措施、模型优势和局限性方面，对本节描述的基于参数耦合的非齐次动态贝叶斯网络模型进行了归纳总结。

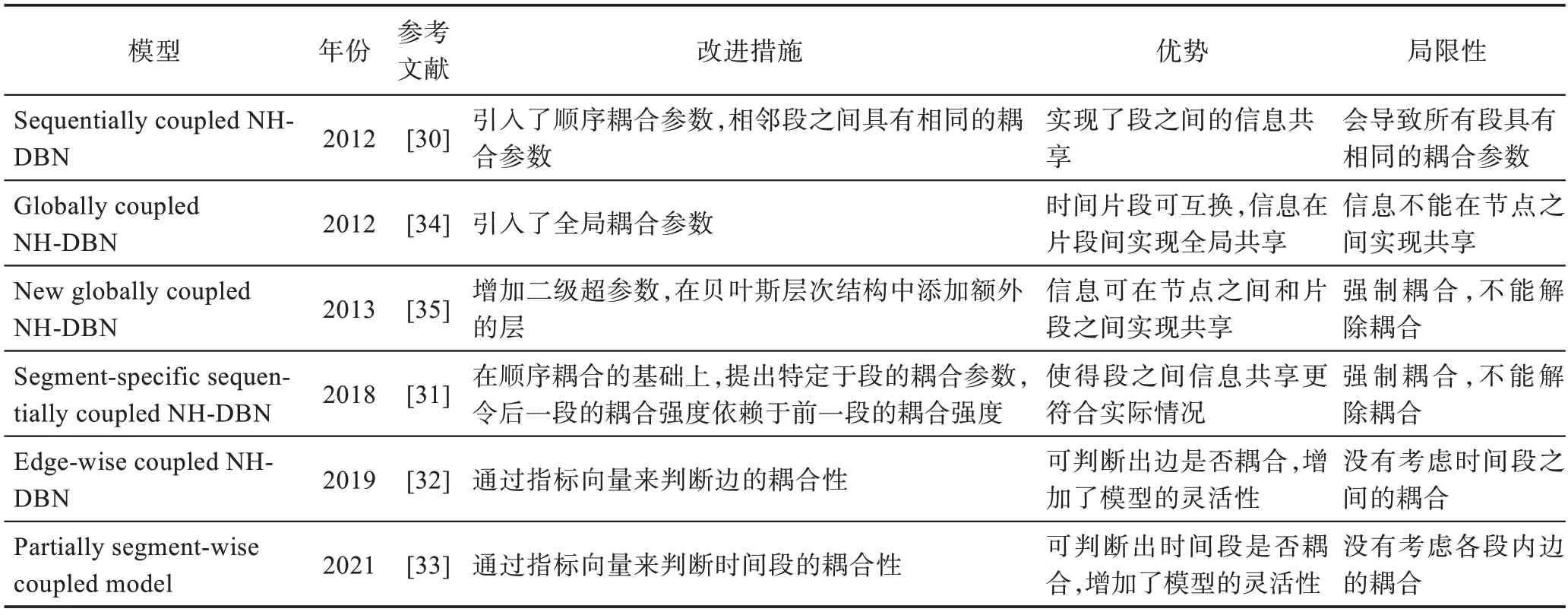
表3 耦合NH-DBN 模型比较Table 3 Comparison of coupled NH-DBN models

4 NH-DBN 模型的性能分析

4.1 评价指标

M(n,j)=1 表示n→j存在调控边，反之M(n,j)=0表示n→j不存在。定义en,j∈(0,1)为每条边的后验概率，E(ξ) 表示后验概率超过阈值ξ所有边的集合。计算每个E(ξ) 对应的真阳性TP[ξ]，假阳性FP[ξ]，假阴性FN[ξ] 。绘制以P[ξ] 为垂直轴，R[ξ]为水平轴的Precision-Recall (PR)曲线，PR 曲线下面积（AUC-PR）作为一种定量测量，较大的AUC-PR 值表示更好的网络构建精度。

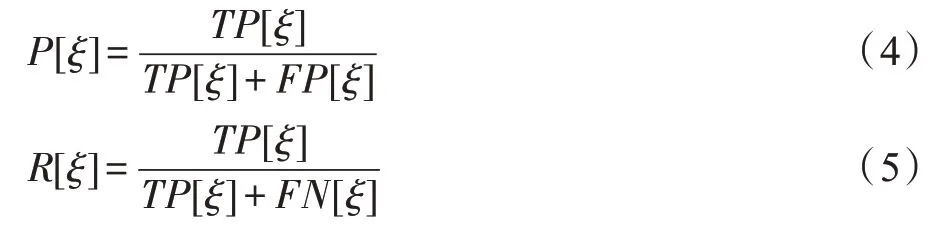
4.2 基于时间片划分方法NH-DBN 模型的性能分析

BGM 模型：（1）网络重建方面，针对静态合成的网络数据，BGM 与BGe[47]和BDe[48]相比之下可以获得更高的网络重建精度。（2）统计学意义方面，通过计算两个分数——贝叶斯因子和预测分布，将这些分数应用于两种不同系统（巨噬细胞受到病毒攻击和植物的昼夜节律）在不同平台（Agilent 和Affymetrix）上获得的基因表达时间序列，发现BGM 的效果往往优于BGe。（3）与内在生物学特征的一致性方面，利用来自骨髓来源的巨噬细胞的基因表达时间序列，重点研究IFN 通路的一个生物学特性明确的子系统，可以证明BGM 能更好地构建通路。

BGMD模型：一方面，通过使用小的合成动态网络发现该模型受伪反馈回路的影响程度更低以及不太容易推断出虚假的自环，因此网络重建精度得到了提升；另一方面，在保持网络结构不变，允许交互参数改变的情况下，BGMD模型比标准BGe 模型和BGM 模型有更好的网络重构精度。

cp-BGe 模型：该模型比经典平稳模型BDe 和BGe 以及其他的非平稳模型有明显的改进。将该模型应用到拟南芥基因表达时间序列中，得到了可靠的数据分段，重建的基因调控网络显示出与生物学文献一致的特征。

New cp-BGe 模型：作者投入了大量的精力来改进和评估MCMC 方案的混合和收敛性，解决了网络结构的采样和变点配置的采样。主要操作如下：一方面，在该模型中，对于父节点和变化点的采样，使用了一种与M-H 方法一致的方法，用来提高MCMC采样的收敛和混合。该方法对于父节点的采样采用玻尔兹曼分布的方法，对于Kn和Vg的采样使用“直接从条件后验分布中抽取变化点的节点特定数量Kn和节点特定分配向量Vn”的方法，主要为了避免M-H采样器会导致较差的收敛和混合，使得模拟往往会陷入局部最优。另一方面，由于基于单边操作的经典结构MCMC的收敛性非常差，引入了一种新的父节点翻转移动，该移动给MCMC的收敛性带来了很大的改进。研究表明，与具有BDe和BGe分数的经典齐次DBN 以及非线性/非平稳模型和BGM模型相比，提出的非齐次cp-BGe模型的性能得到了明显改善。将该模型应用于拟南芥中生物钟调控基因的基因表达时间序列，得出了合理的数据分段，重建的网络显示出与生物学文献一致的特征。

HMM-DBN 模型：首先，对于周期性数据的时间片段划分，HMM-DBN 模型优于MIX-DBN 和GPSDBN。其次，关于酵母网络重构精度，通过对比齐次动态贝叶斯网络（homogeneous-DBN，HOM-DBN）、CPS-DBN、MIX-DBN 和耦合CPS-DBN 模型，HMMDBN 的平均AUC 分数最高，即网络重构精度得到了一定的提升。最后，关于拟南芥基因调控网络的重建，发现了多个和生物学文献一致的基因节点调控边。

4.3 基于耦合参数NH-DBN 模型的性能分析

SC NH-DBN 模型：首先该模型相较于传统的非耦合时变动态贝叶斯网络（time-varying DBN，TVDBN）模型提高了网络重构精度；然后针对果蝇和拟南芥基因表达数据，与传统的非耦合TV-DBN 模型相比，SC NH-DBN 模型对于时间序列的分段产生了更强相关的相互作用参数。此外，还发现SC NH-DBN模型对于（未知）变化点数量的变化具有更强的鲁棒性，即随着推断的变化点数量的增加，网络重建精度保持稳定。

SSC NH-DBN 模型：一方面，该模型与文献[30]中的模型相比，网络的重建精度的确得到了很大提高；另一方面，与M0,0、M0,1、M1,0三个模型进行对比（这三个模型在参数的设定上不同：M0,0是2012 年的SC NH-DBN 模型，M0,1和M1,0是对提出的SSC NHDBN 模型做了修改的模型，M1,0在耦合参数上做了修改，M0,1在超参数上做了修改），实验结果发现，只有SSC NH-DBN 模型对于变点过程超参数是稳健的，即随着推断的变化点数量的增加，其他模型的网络精度会下降，只有SSC NH-DBN 模型的网络重建精度保持较高。

EWC NH-DBN 模型：首先，针对酵母数据，该模型对比其他13种先进模型[21,29-30,49-53]具有更高的网络重构精度（其中包括传统同构DBN，文献[30]和文献[21]提出的模型等）。然后，针对拟南芥数据，该模型学习出了一个网络结构，参考当前的生物学文献资料，拟南芥生物钟网络结构中的重要关键特征是LHY 和TOC1之间的反馈回路。该模型不仅推断出了这一反馈循环，还表明了LHY 对TOC1 的影响不依赖于光，而TOC1 对LHY 的调节作用依赖于光。还进一步发现了ELF3 对TOC1 的调控作用也是光依赖的。

PSC NH-DBN 模型：该模型和非耦模型、文献[30]提出的全局耦合模型、文献[31]提出的特定于段的顺序耦合模型进行了对比。通过对比发现：一是应用在合成数据集以及酵母数据集上，该模型比起其他竞争模型有更好的网络重建精度；二是应用在拟南芥数据集上，学习出来的网络结构中包含已被证实的LHY→ELF3、LHY→ELF4、GI→TOC1、ELF3→PRR3、ELF4→PRR9 等边。

New GC NH-DBN 模型：首先，通过对齐次DBN和非耦合NH-DBN 以及全局耦合NH-DBN 的对比发现，在中、高信噪比情况下，提出的耦合NH-DBN 的网络重构精度优于齐次DBN 和非耦合NH-DBN。然后，改进后的模型比Grzegorczyk 等人的模型MCMC抽样方案收敛得更好，并且达到了更好的网络重构精度。

表4 总结归纳了本章描述的各模型的性能分析。

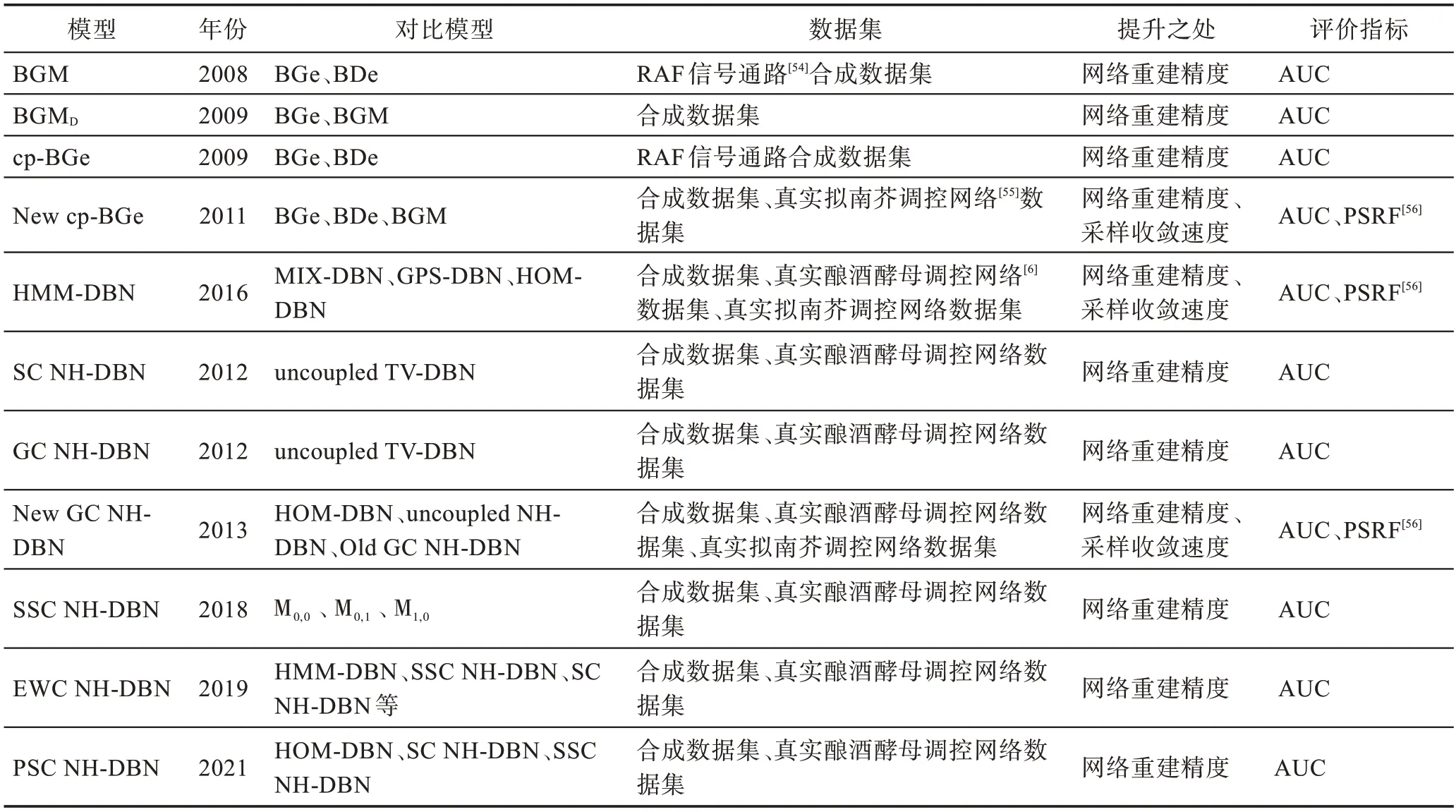
表4 NH-DBN 模型的性能分析Table 4 Performance analysis of NH-DBN models

5 GRN 建模存在的问题及未来研究方向

正如本文中所讨论的，GRN 推断是系统生物学的一个主要挑战，在过去的十几年中，对于GRN 的有效重建，已有大量的建模方法和评价指标，但GRN 推断仍然面临着一些困难与挑战，本文通过对基因调控网络研究现状的认识，总结出其困难与挑战如下：

（1）GRN 的数据处理问题：目前越来越多的基因表达数据集已可获取，那么对于数据的处理也提出了更高要求。首先，维度诅咒使处理大数据集的推理方法受到影响，因此仍然需要更新颖和更有效的算法。维度问题通常伴随着大量先验生物知识的整合，而诸如稀疏性等模型参数对解决这些问题作用不大。与此同时，特征选择对于从大数据集推断GRN 也非常重要。这些参数限制了每个基因的调节器的数量，并使得模型更加复杂。此外，来自单细胞的全向数据的整合仍然具有挑战性，因此需要有标准化的方法。除此之外，多源生物知识的整合存在数据不足的问题，这也是GRN 研究的一个重点。

（2）GRN 建模方法的评估方法问题：GRN 建模方法都有其自身的优势和劣势，为了对它们进行比较，已经做了许多努力，使用这些算法从单一的数据集推断出一个GRN，然后评估其有效性。这些比较需要适当的评估方法来令人满意地确定算法的性能。

（3）GRN 的建模方法问题：系统生物学的研究最终要走向整合的道路，从对简单环路的研究逐步上升到中等网络，乃至真实大型网络的研究具有很重要的现实意义。目前，没有一个单独的GRN 建模方法对所有的问题都表现得很好。由于每个方法只能合理地关注调控网络的一个或几个方面，推断一个感兴趣的网络的最佳做法将几个来源的结果整合到具有逻辑性和人类可读的图形输出中。例如，没有一种方法可以明确地宣称在推断转录靶点、翻译后靶点或驱动某些表型的主调节器方面是绝对最好的。尽管每种方法都有优势，但仔细分析多种方法的结果将为研究者提供对实验结果最完整和最有用的基于GRN的见解。虽然纳入更多的特征和数据集将导致用于推断GRN 的算法和方法的反复改进，但对于科学界来说，最重要的仍然是积极开发可获得的工具。

结合GRN 的建模方法所面临的挑战，提出以下三点未来研究方向：

（1）针对网络结构推断部分，目前存在的非齐次动态贝叶斯模型中，对于父节点的采样随机性较强。在未来的工作中，可以考虑在进行父节点采样前，进行父节点筛选操作。通过利用关联模型（例如互信息、皮尔逊相关系数等）学习基因节点的相关性，获得候选父节点集，进一步提高下一步的父节点采样的准确性以及效率。但是，在处理基因节点较多的数据时，要注意父节点筛选部分的时间复杂度。

（2）针对时间片划分部分，时间片进行有效划分可更好地发掘潜在信息，对于基因网络重建精度可得到有效提升。可对现有的一些时间片划分方式的优缺点进行分析，尝试建立更好的时间片划分方式。转换点的选取就是值得进一步深入研究的问题，可以通过欧式距离、曼哈顿距离等方式对转换点进行选取，从而更有效地划分时间片，时间片的合理划分是提高网络结构重建精度的关键步骤。

（3）针对耦合参数推断学习部分，相关研究表明，目前存在全局耦合、顺序耦合以及特定于段的顺序耦合等耦合参数学习方式。但不同类型的基因时序数据，其耦合程度不同，以及段间、段内数据的耦合程度也是不同的。因此，对于耦合参数的学习方式是未来研究的重点也是难点。未来可以尝试将时间段耦合的概念与边耦合的概念相结合。这两个概念的结合将产生一个高度灵活的新NHDBN 模型，将每个单独的网络边进行部分分段耦合。可以去实证检验这种新的混合模型是否会带来更好的网络重构结果，或者是否存在模型过于灵活的问题。

6 结束语

本文对齐次动态贝叶斯网络的基因调控网络建模方法以及近十几年提出的非齐次动态贝叶斯网络模型进行了综述，并详细地描述了各模型的主要思想和创新点以及分析了各模型的优缺点。然后，介绍了基因调控网络重建的评价指标且着重对非齐次动态贝叶斯网络模型进行了详细的性能分析。非齐次动态贝叶斯建模方法较传统方法得到了更高的准确率，但仍存在若干问题待解决。最后，结合上述内容，阐述了GRN 目前存在的困难与挑战并提出了未来的一些研究方向。希望对当前及未来关于基因调控网络建模的研究工作有所帮助。